WEIGHT ESTIMATION AND CLASSIFICATION OF MILLED

RICE USING SUPPORT VECTOR MACHINES

Oliver C. Agustin and Byung-Joo Oh

Department of Electronic Engineering, Hannam University, 133 Ojeong-dong, Daeduk-gu, Daejeon City, Korea

Keywords: Support vector machines, Milled rice analysis.

Abstract: This paper presents a method for weight estimation and classification of milled rice kernels using support

vector machines. Shape descriptors are used as input features for determining the grade factors based on

physical shapes such as headrice, broken kernel, and brewer. Colour histogram is extracted from milled rice

image to obtain 24 colour features in RGB and Cielab colour spaces. We built a support vector regression

(SVR) model for estimating rice kernel weight and support vector classifier (SVC) for rice defectives.

Results showed that in real data, the performance of SVR is better than linear regression (LR) with a mean

square error (MSE), mean absolute error (MAE) and correlation coefficient of 78.35x10

-3

, 0.206 and

0.9943, respectively. In determining grade factors based on colour appearance (rice defectives), SVC

outperforms the generalized regression neural network (GRNN) with an accuracy of 98.86%.

1 INTRODUCTION

Machine vision quality evaluation systems

objectively measure and classify various agricultural

(Zapotocznya, Zielinskaa et al.) and food products

(Timmermans, 1998). Vision-based methods are

objective, non-destructive and can assess the visual

quality characteristics of agricultural grains (Zayas,

Martin et al., 1996; Ni, Paulsen et al., 1997)

especially, milled rice (Yadav and Jindal, 2001) with

high accuracy.

Existing rice quality evaluation systems perform

neural network-based classification techniques in

which grains are classified in bulk (Visen, Paliwal et

al., 2004). This method makes it difficult to

determine the number of rice kernels and provide a

way to estimate the weight of rice kernels.

Difficulties arise when rice quality evaluation

standards require that the grade factors be expressed

as a percentage by weight of defective rice content

that are present in milled rice grain samples.

Continuous improvement of the classification

accuracy in evaluating these quality factors is

important.

The goal of this paper is to present the support

vector machines (SVM) to achieve the purpose of

this paper by: a) building an SVR model for weight

estimation of milled rice kernel, b) SVC model for

classifying milled rice defectives, and c) compare

the performance of the proposed models with

existing methods used in (Agustin and Oh, 2008).

2 RICE QUALITY AND

EVALUATION FRAMEWORK

Rice quality defectives are classified according to

various categories such as discoloured, chalky,

sound, broken, red, and damaged kernels. Headrice

is defined as kernel or piece of kernel with its length

equal to or greater than 75% of the average length

(grain size) of unbroken kernel. Broken kernels are

kernels below 75% of the grain size. Brewers are

small pieces or particles of kernels that pass through

a sieve having round perforations of 1.4 mm in

diameter. More information about rice defectives

and rice grading standards that we adopt are

available in (2002).

Rice image processing in stage 1 Figure 1

acquire images from various image sources.

Background segmentation is performed in stage 1 to

filter the object of interest from the acquired image.

Once unimportant features are removed, colour

image is converted into binary image format to

recover the shape of rice kernels

377

Agustin O. and Oh B. (2009).

WEIGHT ESTIMATION AND CLASSIFICATION OF MILLED RICE USING SUPPORT VECTOR MACHINES.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 377-380

DOI: 10.5220/0001755803770380

 SciTePress

Figure 1: Proposed evaluation framework for milled rice

grains weight estimation and classification using SVM.

Figure 2a shows the acquired image and in

Figure 2b the rice kernels with the background-

segmented image. Note that non-trivial pink

background colour was used to preserve all features

that would have been removed when black or white

background is used (Agustin and Oh, 2008).

Figure 2: Acquired rice image and background

segmentation.

In stage 2, shape analysis is performed to get the

morphological properties of the rice. Area,

perimeter, major axis, minor axis, feret diameter,

and roundness comprise the geometric features.

Stage 3 performs weight estimation based on the

given area of rice kernel image. In defectives

classifier of stage 4, each segmented rice kernels are

evaluated according to rice defectives categories.

Having estimated the total weight for each class, rice

grade evaluation is performed in stage 5 using the

milled rice grading standards in (NFA, 2002).

3 SUPPORT VECTOR

MACHINES

A regression model was implemented in (Yadav and

Jindal, 2001) to find a relationship between headrice

yield and characteristic dimension. In (Agustin and

Oh, 2008), linear regression was able to estimate

kernel weight using rice blob area and Generalized

Regression Neural Network (GRNN) for

classification of rice defectives. In this paper, we

extend the application of SVM to milled rice grain

quality evaluation.

In its basic formulation, SVM (Vapnik, 2000) are

linear functions of the form

() ,

xb=+wxi where

wxi is the inner product between the weight

vector w and the input vector x. SVM is commonly

used for binary classification by setting the class to 1

() 0fx> and -1 if () 0fx≤ . The underlying

principle behind SVM is to choose hyperplanes that

separate positive and negative examples while

maximizing the margin between two classes and

choosing a linear separation in feature space.

We adopted the C-Support Vector Classification

(C-SVC) (Scholkopf, Smola et al., 2000) to perform

classification of milled rice defectives. The decision

function of C-SVC is expressed in the equation as::

sgn ( , )

ii i j

Ks b

⎛⎞

⎜⎟

⎝⎠

∑

(1)

where

(, )

is a kernel function,

N refers to

the number of support vectors as a result of training,

are the support vectors, and b is the bias term.

A “one-against-one” approach by training a

binary SVM in (1) for any two classes of data to

obtain the equation in (2). For a k-class problem,

there are k(k-1)/2 decision functions. In the

prediction stage, a voting strategy is used where a

testing data point x, is designated to be in a class

with the maximum number of votes (Hsu and Lin,

2002):

(

)

sgn (w ) (x)+b

ij T ij

. (2)

Equation (2) signifies that if x is in the ith class,

then the vote for the ith class is added by one.

Otherwise, jth is increased by one. After which, x is

predicted in the class with the largest vote.

Finally, we address the milled rice weight

estimation problem using v-Support Vector

Regression (v-SVR) (Smola and Schölkopf, 2004).

The regression estimate takes the form

() ( ) ( ,)

ii i

xKxxb

αα

−+

∑

. (3)

The expression in (3) estimates the weight of

milled rice grain by means of shape feature (area of

milled rice blob) as the only input feature.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

378

4 RESULT AND DISCUSSION

To compare the performance of the SVM classifier

with a neural network classifier, we built a GRNN

classifier (Agustin and Oh, 2007). Optimal

Parameters for SVM and Kernel Function Selection

The best way to find these parameter values is to do

an exhaustive grid search. An survey has been

published in (Chang and Lin, 2001) and

recommending the RBF kernel in SVM. We

evaluated varies kernel functions and the results are

summarized in the Table 1 showing parameters and

kernel function that will give maximum accuracy for

milled rice classification.

Table 1: Optimal parameter for leading to highest

classification accuracy in SVC with different kernels.

Kernel Penalt

(C)

amma r De

ree(d) Accurac

(%)

Linear 32 0.00781250 NA NA 93.13

Polynomial NA NA 25 4 93.13

RBF 32768 0.00781250 NA NA 93.38

Sigmoid 32768 0.00195313 0

A 92.95

4.1 Data and Features Set

The dataset given in Table 2 is composed of 4,979

training instances and 2,011 test instances. Milled

rice categories contain an equal number of instances.

The features are scaled in the range {-1, 1} to

prevent attributes with larger values to dominate

smaller ones. Similar scaling factor is applied to

testing data. Numeric values were assigned to

different classes.

Table 2: Training and test data used for SVC and GRNN

classifiers.

Categories Samples Training Test

Damaged 1165 826 339

Good 1165 827 338

Paddy(Palay) 1165 814 351

Chalky 1165 850 315

Discolored 1165 831 334

Red Kernel 1165 831 334

Total: 6990 4979 2011

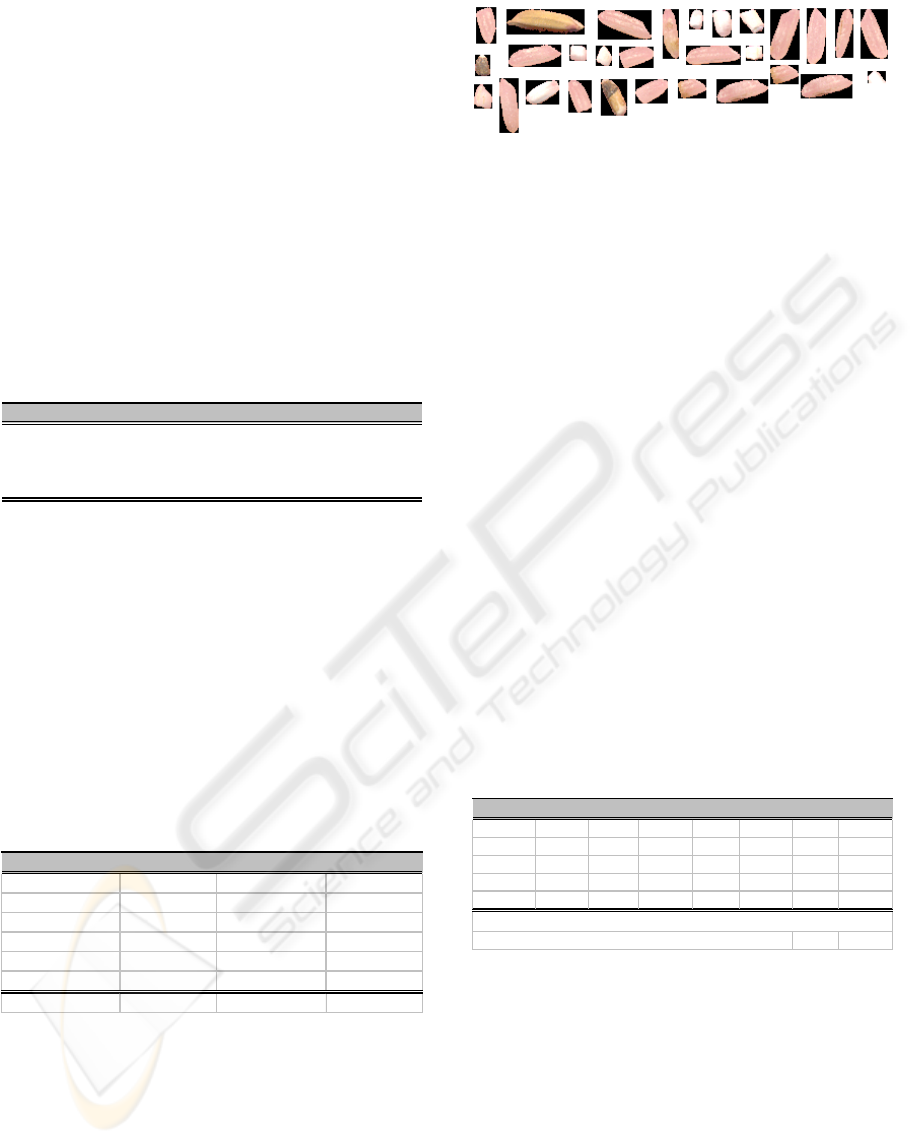
Figure 3 presents images of the extracted milled rice

grains from the image sample as input data to stage

2 (see the rice evaluation framework in Figure 1).

Six geometric features and 24 colour features are

then extracted for each rice kernel images. Shape

descriptors such as area, perimeter, major axis,

minor axis, feret diameter, and roundness define the

geometric features while the mean, median, range,

and standard deviation of each kernel images

Figure 3: Extracted colour rice blobs ready for features

extraction.

in RGB and Cielab colour spaces having a total of

24 colour features.

We used thirty seven rice images (1407×1776

pixels, 24-bit bitmap format) as the source of our

real dataset in evaluating the performance of the

regression and classification models. The images

contain milled rice kernels of different defectives

types whose sample weight varies between 0.5

grams to 10.0 grams. For background segmentation,

we use the optimal color range in scaled Cielab

space {255, 165, 255} to delete background pixels

but we also use other ranges (e.g., {255, 160, 255}

and {255, 170, 255}) to test the or SVM regression

and classification model when the filter ranges

deviated from the optimal threshold.

4.2 Regression

Table 3 shows various results of weight estimation.

For SVR, we obtain an MSE, MAE, and correlation

coefficient of 78.35x10

-3

, 0.206 and 0.9943,

respectively.

Table 3: Weight estimation result between SVR and LR

using different parameters for background segmentation.

Defectives

ACTUAL LR/160 SVR/160 LR/165 SVR/165 LR/170 SVR/170

Chalky 5.23 5.68 5.65 5.79 5.76 5.90 5.87

Good 16.22 16.22 16.08 16.46 16.31 16.68 16.53

Immature 23.54 27.17 26.99 27.64 27.46 28.09 27.90

Red 50.02 49.65 49.23 51.16 50.72 52.12 51.66

yellow 64.08 66.10 65.57 67.28 66.73 68.31 67.74

Threshold values used in background subtraction are 160, 165 and 170

Note: All units are in grams, LR - Linear Regression, SVR - Support Vector Regression

LR, on the other hand, resulted to an MSE,

MAE, and correlation coefficient, of 87.64x10

-3

0.220 and 0.9945, respectively. Based on these

results, SVR slightly outperforms LR. There is one

excellent characteristic of SVR which makes it a

desirable approach for milled rice weight estimation.

The deviation of the prediction error is lesser than

LR when the threshold value used in background

segmentation deviates from the optimal value.

WEIGHT ESTIMATION AND CLASSIFICATION OF MILLED RICE USING SUPPORT VECTOR MACHINES

379

4.3 Classification

The confusion matrix for SVC is shown in Table 4

using the test data in Table 2. We achieved an

accuracy of 98.86% (1988/2011).

Table 4: SVC Classification matrix for milled rice kernels

with an accuracy of 98.86%.

Dmgd Good Palay Chalky Disc Red Accuracy(%)

Damgd 333 0 1 2 3 0 98.23

Good 0 338 0 0 0 0 100.00

Paddy 1 0 350 0 0 0 99.72

Chalky 7 2 0 306 0 0 97.14

Disc 3 0 0 0 331 0 99.10

Red

2 2 0 0 0 330 98.80

Similarly, we did a performance evaluation on

GRNN classifier using the same test data. Different

combination of parameter values were tried

including the use of genetic algorithm to find the

optimal smoothing factors. The performance of the

GRNN model for each rice defectives classification

is presented in Table 5 having an overall accuracy of

91.84% (1847/2011).

Table 5: GRNN classification matrix for milled rice

kernels with an overall accuracy of 91.84%.

Dmgd Good Palay Chalky Disc Red Accuracy(%)

Damgd 276 24 13 13 12 1 81.42

Good 0 327 9 1 0 1 96.75

Paddy 3 5 339 2 2 0 96.58

Chalky 10 2 6 297 0 0 94.29

Disc 3 4 8 12 303 4 90.72

Red

6 3 5 5 10 305 91.32

5 CONCLUSIONS

Judging from the weight estimation capability of

SVR and LR, the performance of proposed model

has been found to perform better especially when

segmentation threshold drifts away from the optimal

value. SVR always has an estimate closer to the

measured value than the LR model. The proposed

SVC model for classifying milled rice defectives far

exceeds the performance of the neural network

counterpart with an accuracy of 98.86% against

88.76% of GRNN using data that was never used for

training.

ACKNOWLEDGEMENTS

This work is supported by a grant from Security

Engineering Research Center of Ministry of

Knowledge Economy and Hannam University.

REFERENCES

Agustin, O. C. and B. J. Oh (2007). "Applications of Ward

Network and GRNN for Corn Quality Classification."

Journal of Korean Institute of Information Technology

5(4): 218-225.

Agustin, O. C. and B. J. Oh (2008). Automatic Milled

Rice Quality Analysis. The 2nd International

Workshop on Network Assurance (NA 2008), Hainan

Island, China, IEEE CS Proceedings.

Chang, C. C. and C. J. Lin (2001). "LIBSVM: A library

for support vector machines."

Hsu, C.-W. and C.-J. Lin (2002). "A comparison of

methods for multiclass support vector machines."

IEEE Transactions on Neural Networks 13(2): 415-

425.

NFA (2002). Philippine Grains Standardization Program,

National Food Authority.

Ni, B., M. R. Paulsen, et al. (1997). "Design of an

automated corn kernel inspection system for machine

vision." Transactions of the ASAE 40(2): 491–497.

Scholkopf, B., A. J. Smola, et al. (2000). New Support

Vector Algorithms, MIT Press. 12: 1207-1245.

Smola, A. J. and B. Schölkopf (2004). "A tutorial on

support vector regression." Statistics and Computing

14(3): 199-222.

Timmermans, A. J. M. (1998). "Computer vision system

for online sorting of pot plants based on learning

techniques." Acta Horticulturae 421: 91-98.

Vapnik, V. N. (2000). The Nature of Statistical Learning

Theory, Springer.

Visen, N. S., J. Paliwal, et al. (2004). "Image analysis of

bulk grain samples using neural networks." Canadian

Biosystems Engineering 46: 7.11-7.15.

Yadav, B. K. and V. K. Jindal (2001). "Monitoring

Milling Quality of Rice by Image Analysis."

Computers and Electronics in Agriculture 33(1): 19-

33.

Zapotocznya, P., M. Zielinskaa, et al. (2008). "Application

of image analysis for the Varietal Classification of

Barley: Morphological features." Journal of Cereal

Science 48(1): 4-9.

Zayas, I. Y., C. R. Martin, et al. (1996). "Wheat

classification using image analysis and crush force

parameters." Transactions of the ASAE 6(39 ): 2199-

2004.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

380