
INDOOR PTZ CAMERA CALIBRATION
WITH CONCURRENT PT AXES
Jordi Sanchez-Riera, Jordi Salvador and Josep R. Casas
Image Processing Group, UPC – Technical University of Catalonia
Jordi Girona 1-3, edifici D5, 08034 Barcelona
Keywords:
Pan, Tilt, Zoom, Active camera calibration.
Abstract:
The introduction of active (pan-tilt-zoom or PTZ) cameras in Smart Rooms in addition to fixed static cameras
allows to improve resolution in volumetric reconstruction, adding the capability to track smaller objects with
higher precision in actual 3D world coordinates. To accomplish this goal, precise camera calibration data
should be available for any pan, tilt, and zoom settings of each PTZ camera. The PTZ calibration method pro-
posed in this paper introduces a novel solution to the problem of computing extrinsic and intrinsic parameters
for active cameras. We first determine the rotation center of the camera expressed under an arbitrary world
coordinate origin. Then, we obtain an equation relating any rotation of the camera with the movement of the
principal point to define extrinsic parameters for any value of pan and tilt. Once this position is determined,
we compute how intrinsic parameters change as a function of zoom. We validate our method by evaluating the
re-projection error and its stability for points inside and outside the calibration set.
1 INTRODUCTION
Smart Rooms equipped with multiple calibrated cam-
eras allow visual observation of the scene for appli-
cation to multi-modal interfaces in human-computer
interaction environments. Static cameras with wide-
angle lenses may be used for far-field volumetric anal-
ysis of humans and objects in the room. Wide angle
lenses might provide maximum room coverage, but
the resolution of the images from these far-field static
cameras is somewhat limited. The introduction of
pan-tilt-zoom (PTZ) cameras permits a more detailed
analysis of moving objects of interest by zooming in
on the desired positions. In this context, calibration
of the PTZ cameras for any pan, tilt, and zoom set-
tings is fundamental to referring the images provided
by these cameras to the working geometry of the ac-
tual 3D world, commonly employed by static cam-
eras.
Our research group has built a room equipped with six
wide-angle static cameras. The purpose of the static
cameras is the computation of a 3D volumetric re-
construction of the foreground elements in the room
by means of background subtraction techniques fol-
lowed by shape-from-silhouette. The volumetric data
resulting from this sensor fusion process is exploited
by different tracking and analysis algorithms working
in the actual 3D world coordinates of the room. With
wide angle lenses spatial room coverage from multi-
ple cameras is almost complete, but the precision of
the volumetric data is restricted by the resolution of
the camera images. Feature extraction analysis op-
erates at a coarse spatial scale, and cannot obtain de-
tailed information, such as the positions of fingers and
hands, which might correspond to convex volumet-
ric blobs in the volumetric representation. The intro-
duction of PTZ cameras in the Smart Room helps to
provide a higher resolution volumetric reconstruction
for hand and gesture recognition algorithms. Hand
movements are closely followed by means of real-
time adjustment of pan and tilt. The calibration of
PTZ cameras is fundamental to referring their images
to the common 3D geometry of the computed volu-
metric data.
Camera calibration methods can be divided into two
groups. The first group makes use of a calibration
pattern, such as a checkerboard, located at a known
3D world position. Calibration parameters are then
inferred from the detected pattern points in order to
calibrate either a single camera (Tsai, 1987; Zhang,
2000; Heikkila, 2000), or several cameras simultane-
ously (Svoboda et al., 2005). The disadvantage of
methods based on knowledge of the calibration pat-
tern position is that they might not be convenient for
10
Sanchez-Riera J., Salvador J. and R. Casas J. (2009).
INDOOR PTZ CAMERA CALIBRATION WITH CONCURRENT PT AXES.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 10-15
DOI: 10.5220/0001754900100015
Copyright
c
SciTePress

large focal lengths.
The second group of methods, also known as auto-
calibration or self-calibration, may also use a calibra-
tion pattern, but in any case the 3D world position
is not known (Hartley and Zisserman, 2000; Agapito
et al., 1999). These methods are more difficult to
implement due to geometrical complexity problems,
such as finding the absolute conic.
Most of the methods cited above have been developed
for static cameras. Calibration of active cameras faces
new challenges, such as computing variation of intrin-
sic and extrinsic parameters, respectively, as a func-
tion of the zoom value and the rotation (pan and tilt)
angles. Effective calibration of the varying parame-
ters for the PTZ cameras requires adaptation of the
algorithms developed for static cameras.
Intrinsics Calibration for PTZs. One approach for
zoom calibration considers each zoom position as a
static camera and then calibrates the PTZ as multi-
ple static cameras. (Willson, 1994) provides a study
on zoom calibration describing the changes in focal
length, principal point, and focus based on Tsai cal-
ibration (Tsai, 1987). The large number of possible
combinations for zoom and focus values makes the
computation of intrinsic parameters ineffective. Other
approaches limit the re-projection error as described
in (Chen et al., 2001), which proposes the calibration
of extreme settings followed by the comparison of the
re-projection error with an arbitrary threshold. Posi-
tions with errors above the threshold are re-calibrated
with a mid point and the extreme. The process is
repeated until the range of zoom and focus settings
is below the re-projection error threshold. A quar-
tic function is finally found to best match the ob-
tained parameters. However, the strategy of multi-
ple static cameras presents problems with increasing
zoom values, that reduce the constraints needed to
solve the equations making results inconsistent (Ruiz
et al., 2002). Huang (Huang et al., 2007) proposes an
algorithm for cameras with telephoto lenses to face
this problem.
An alternative approach for calibrating intrinsic pa-
rameters under varying zoom values is the separate
computation of focal length and principal point al-
though, for the latter, (Li and Lavest, 1996) claim that
calibration results are not significantly affected if the
principal point is assumed to be constant.
Extrinsics Calibration for PTZs. Extrinsic param-
eters are important for the correct application of in-
trinsic calibration results, but the methods mentioned
so far focus on the computation of intrinsic parame-
ters without describing how to compute extrinsics in
much detail. (Sinha and Pollefeys, 2004) proposes
computing both intrinsics and extrinsics in an outdoor
environment using an homography between images
acquired at different pan, tilt and zoom. (Davis and
Chen, 2003) compute extrinsics by finding the cam-
era rotation axis. Further references for computing
both extrinsics and intrinsics for surveillance applica-
tions are (Kim et al., 2006; Senior et al., 2005; Lim
et al., 2003).
Proposal. To overcome the problems of the differ-
ent methods mentioned above for the calibration of
active cameras, we propose to find the rotation center
of the camera. Once the rotation center is known, ex-
trinsic parameters can be found by simply applying a
geometric formula, and then intrinsic parameters can
be determined by a simple bundle adjustment.
In the following, we first review the specifics of the
active camera model, then describe the proposed cal-
ibration method in Section 3, and finally we present
the experimental results in Section 4 and draw con-
clusions to close the paper.
2 THE PTZ CAMERA MODEL
Camera calibration is important to the relation of the
physical world with the images captured by the cam-
era. This relation is defined by a mathematical model.
The pin-hole camera model is based on the perspec-
tive transform (a 3x3 matrix K) explaining the rela-
tion from the 3D world to the 2D image plane. Unfor-
tunately, real camera optics introduce distortion that
must be modeled and corrected. The camera model
is not complete without positioning the camera in the
physical world according to arbitrarily chosen world
coordinates. For this we need to know the rotation (a
3x3 matrix R) and translation (a 3x1 vector T) of the
camera coordinates with respect to the world coordi-
nates.
The equation resulting from the above description re-
lates the 3D homogeneous points X in world coor-
dinates with 2D homogeneous points x in the image
plane as follows:
x = K[R|T]X (1)
2.1 Extrinsic Parameters
For PTZ cameras, R and T depend on how the prin-
cipal point changes with pan and tilt movements. If
the principal point is different from the rotation cen-
ter of the camera (e.g. by a shift r in the optical axis),
then any change in the pan (or tilt) angle of α degrees
will produce a rotation and a translation of the prin-
cipal point, which, due to the mechanics of the PTZ
INDOOR PTZ CAMERA CALIBRATION WITH CONCURRENT PT AXES
11
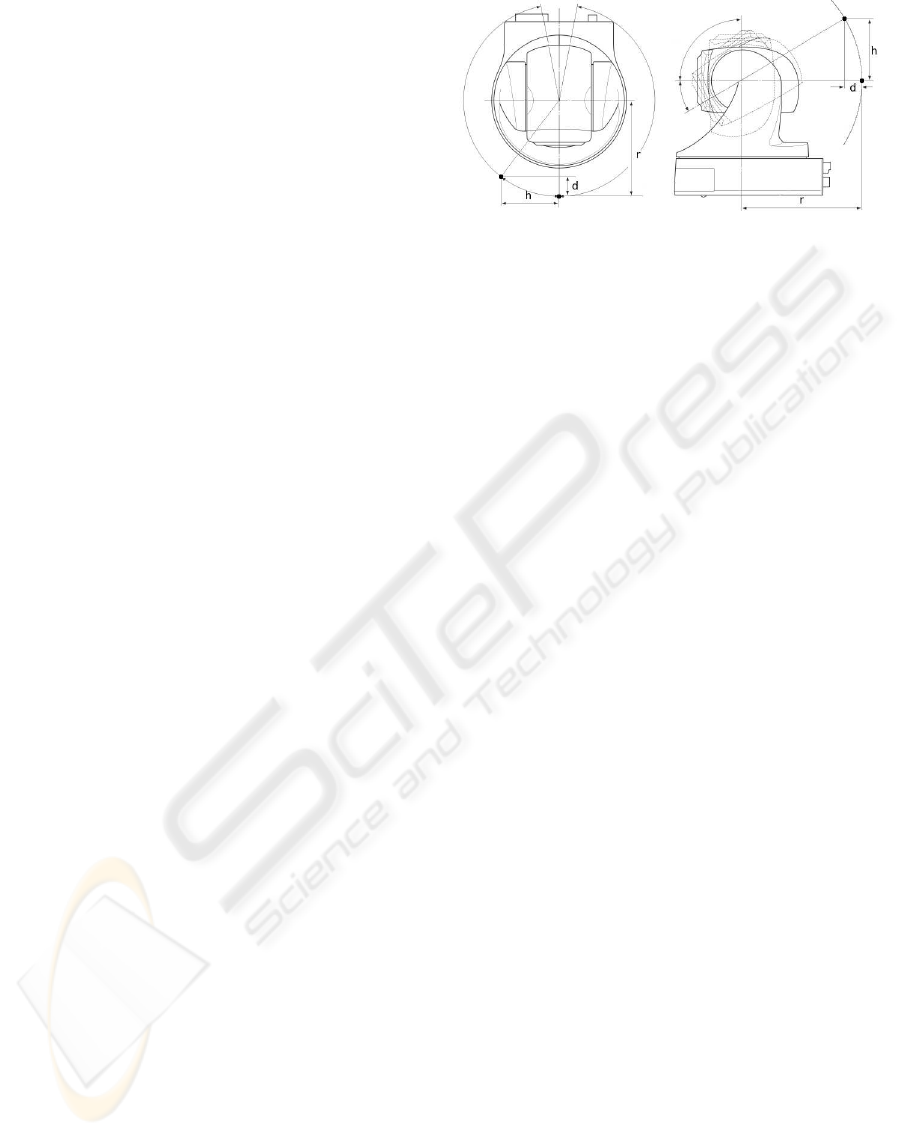
camera, will describe a sphere of radius r centered
on the rotation center. Considering R
r
and T
r
, the ro-
tation and translation describing the position of the
rotation center as reference position, any pan (or tilt)
movement will produce an additional rotation R
a
and
translation T
a
describing the position of the principal
point.
The reference is defined to be at pan and tilt zero,
then the rotation R
a
and translation T
a
should be ap-
plied to the 3D homogeneous points X. Note that this
transform is not a trivial operation. When pan and
tilt displacement occur at the same time, two rota-
tion matrices are needed and the order in which ma-
trices are multiplied produces different results. Thus,
the transform necessary to express the 3D homoge-
neous points X in correct principal point origin coor-
dinates must be applied in the following order: Rotate
the points R
r
and translate T
r
, then apply rotation R
a
and after the translation T
a
, finally translate the points
back to the origin with transform T.
R
a
= (R
t
R
p
) (2)
R = R
r
(3)
T
a
= T
p
+ T
t
+ [0,0,r]
T
(4)
T = T
a
+ T
r
(5)
In the next subsections we describe the parameters in
Equations (2-5) and the effects of pan and tilt inde-
pendently. Our coordinate axis election is described
considering z for the optical axis (in the depth direc-
tion) and x, y for the Cartesian coordinates on the im-
age plane.
2.1.1 Pan and Tilt Movements
Figure 1 represents the displacement of the princi-
pal point when either pan or tilt changes. When pan
changes by α degrees, it introduces a rotation R
p
(α)
and a translation T
p
(α) parameterized by α:
R
p
(α) =
cos(α) 0 sin(α)
0 1 0
−sin(α) 0 cos(α)
(6)
T
p
(α) =
0
h
d
=
0
rsin(α)
−r(1− cos(α))
(7)
When tilt changes by β degrees, it introduces a rota-
tion R
t
(β) and a translation T
t
(β) parameterized by β:
R
t
(β) =
1 0 0
0 cos(β) −sin(β)
0 sin(β) cos(β)
(8)
Figure 1: Principal point displacement (black dot) due to
pan (left image) and tilt (right image).
T
t
(β) =
h
0
d
=
rsin(β)
0
−r(1− cos(β))
(9)
2.2 Intrinsic Parameters
The perspective transform provides a 3x3 matrix, K,
mapping the 3D space to the 2D camera plane assum-
ing the pin-hole camera model. This mapping is char-
acterized by the principal point and the focal length.
The principal point (p
x
, p
y
) is located at the intersec-
tion of the optical axis with the image plane. Usually
the camera is designed so that the principal point is
at the center of the image, but it may shift depending
on the camera optics and zoom settings. The focal
length is the distance between the principal point and
the focal point. Measured in pixels, the focal length is
represented by two components ( f
x
, f
y
) (the “aspect
ratio” f
y
/ f
x
is different from 1 only for non-square
pixels). For PTZ cameras, we may assume that all the
intrinsic parameters are a function of zoom:
K(z) =
f
x
(z) sk(z) p
x
(z)
0 f
y
(z) p
y
(z)
0 0 1
(10)
sk represents the skew coefficient defining the angle
between the x and y image axes. Further, we must
consider the distortion introduced by camera lenses,
represented by four parameters, two for radial and two
for tangential distortion, as described in (Bouguet,
2007).
3 CALIBRATION METHOD
The first goal of our calibration method is to find the
rotation center of the camera and its distance to the
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
12

principal point. Then, with just a geometric trans-
form, we can obtain the extrinsic parameters for any
given pan, tilt position. Once this is done, we can
focus on the intrinsic parameters. Using the extrinsic
paramters already found as the valid camera world po-
sition, we can obtain the intrinsic parameters consid-
ering that, when zoom changes, intrinsic parameters
also change.
To compute the rotation center and its distance to the
principal point, first we place the calibration pattern
in a known and measured position in the room respect
our world origin, and we take some images at sev-
eral known pan and tilt positions at zoom zero (widest
lens). One of the images is taken as reference and the
others are described by its relative pan and tilt position
with respect to the reference. Then a bundle adjust-
ment, shown in Equation (11) is applied to minimize
the reprojection error.
n
∑
i=1
m
∑
j=1
||(x
ij
− ˆx(R
i
,R
pi
,R
ti
,T
i
,T
pi
,T
ti
,X
j
,kc,a
p
,a
t
)||
2
(11)
where ˆx(R
i
,..) is the projection of point X
j
in image
i according to Equation (1) with modifications ex-
plained in Section 2.1 and, using four parameters for
lens distortion kc. R
i
, T
i
are the rotation and transla-
tion matrices for the reference image. R
pi
, R
ti
and T
pi
,
T
ti
are the additional rotation and translation matrices
due to the relative pan and tilt movements, described
in Equations (6-9). Our formulation assumes there
are n images with m points in each image. Depend-
ing on the camera position, it will not be possible to
take images of the calibration pattern at pan and tilt
zero, thus a
p
and a
t
describe the pan and tilt of the
reference image respect the zero position.
In order to reach convergence, it is important to start
from a good initial guess of the parameters’ values. In
our case the initial guess for the intrinsic and extrin-
sic parameters is obtained with (Bouguet, 2007), al-
though any other method, such as (Tsai, 1987), could
be equally valid.
With the same principle, we can consider the values
of rotation center and radius just found after the previ-
ous error minimization as an initial guess for a second
bundle adjustment. In this case, we aim at minimizing
error with respect to all the parameters: Intrinsic and
extrinsic (rotation center and radius). This minimiza-
tion is computed on the functional shown in Equa-
tion (12).
n
∑
i=1
m
∑
j=1
||(x
ij
− ˆx(K, R
i
,R
pi
,R
ti
,T
i
,T
pi
,T
ti
,X
j
,kc,a
p
,a
t
)||
2
(12)
Note that the intrinsic parameters K, are not present
in the Equation (11). With a calibrated PT (pan-
tilt) camera after this second minimization, we need
to calibrate the intrinsic parameters as a function of
zoom. For this purpose, we take some images at dif-
ferent zoom values of the calibration pattern in the
previous reference position. As we increase the zoom,
the calibration pattern ends up outside of the image,
therefore, a smaller calibration pattern is used. This
second pattern must be aligned with the previous one
to keep it in the same measured position. In this case,
the minimized functional is shown in Equation (13).
m
∑
j=1
||(x
j
− ˆx(K(z),X
j
)||
2
(13)
Note that only one image is used each time and only
intrinsic parameters are minimized. In our particular
case, the camera has 1000 step positions for zoom.
This is a large number of values and it would not be a
good idea to perform the minimization for all the pos-
sible values. Therefore, we take the images sampling
the whole zoom range at equal intervals. With this, we
obtain the intrinsic parameters for some of the values
of zoom and then, we can fit a function. This function
is as simple as a polynomial of n degrees and n+ 1
coefficients.
4 RESULTS
The proposed algorithm has been implemented in
Matlab as an extension of the (Bouguet, 2007) tool-
box. In order to test the correctness and limits of
the method, we have studied how pan and tilt range
affects the re-projection error and have determined
which is the optimal number of degrees to fit a func-
tion and the optimal sampling of the zoom range. An-
other test performed to ensure that the correct param-
eters are found consists in the evaluation of the repro-
jection error of a known 3D position different from
those used to calibrate the camera, in the Smart Room.
For all recordings we have used two different calibra-
tion patterns consisting of black and white squares.
The images have been grabbed using a Sony-EVI D70
camera, controlled with the Evi-Lib library (EVI-Lib,
2006) for adjustment of pan, tilt, and zoom.
Depending on the distance from the calibration pat-
tern to the camera, the range of pan and tilt, such that
the camera is able to grab an image of the whole pat-
tern, will vary. In the selected pattern position, we are
able to capture a maximum range of 35 degrees from
one side to another of pan, and a maximum range of
20 degrees from one side to another of tilt. In Figure 2
we have represented the re-projection error (y-axis)
as a function of pan range (x-axis) and tilt range (the
INDOOR PTZ CAMERA CALIBRATION WITH CONCURRENT PT AXES
13
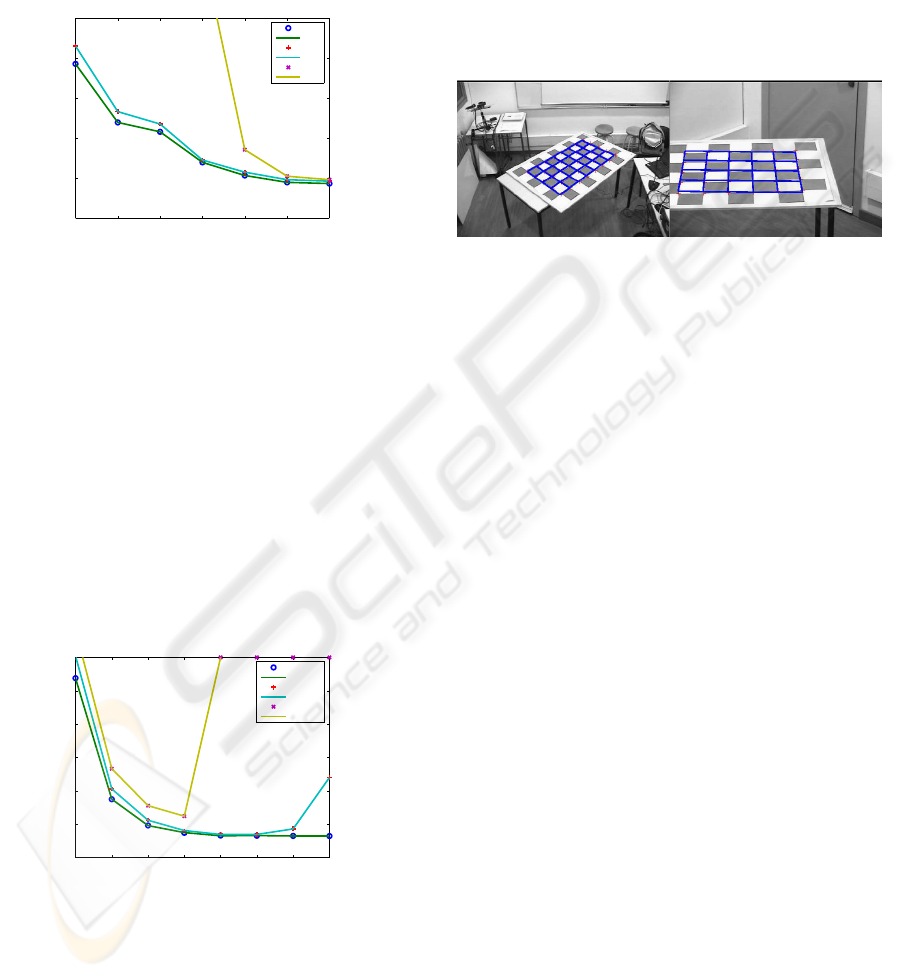
lines drawn). Note that, if for any reason, we are not
able to work with a tilt range larger than 10, the pan
range needs to be at least 25 to keep re-projection er-
ror below 3 pixels. For a tilt range larger than 10, the
algorithm is more flexible, allowing more variability
for pan range and still keeping a re-projection error
below 1.5 pixels.
5 10 15 20 25 30 35
0.5
1
1.5
2
2.5
3
pan range
reprojection error
tilt 20
tilt 15
tilt 10
Figure 2: Reprojection error for extrinsic parameters as a
function of pan and tilt.
In Figure 3 we have represented the reprojection error
(y-axis) as a function of the number of coefficients
(x-axis) and intervals of zoom sampling (the lines
drawn). For intervals of 25 or 50 steps, the results
are very similar, except for coefficients larger than 14,
when re-projection error of the line corresponding to
50 steps increases. This is because with 50 steps, over
a range of 1000 possible steps, there is not enough
data to fit a function with more than 14 coefficients.
For similar reasons, when data is taken from intervals
of 100 steps, it is not possible to fit a function with an
arbitrary large number of coefficients. With a small
number of coeffs. (e.g. 4), the error is larger than 5
pixels.
4 6 8 10 12 14 16 18
2
2.5
3
3.5
4
4.5
5
reprojection error
degrees
steps 25
steps 50
steps 100
Figure 3: Reprojection error for intrinsic parameters for dif-
ferent polynomial degrees.
With camera parameters within correct re-projection
error margins, it is also important to acknowledge to
what extent the model is able to reproduce the same
results for different positions than those used to cal-
ibrate the camera. For this purpose a second set of
images has been acquired with the calibration pat-
tern at different position. Figure 4 shows two exam-
ples of the re-projection error at different zoom val-
ues. Taking 40 different images at random positions
with zoom zero (shortest focal length), we get a re-
projection error of 1.20 pixels with a standard devia-
tion of 0.56 pixels while taking 40 images at different
zoom positions the re-projection error is 2.45 pixels
with a standard deviation of 2.64 pixels. This proves
that the re-projection error is very close to the values
obtained during calibration.
Figure 4: Grid projection. Left image zoom 0, error = 0.93
pixels. Right image zoom 550, error 1.83 pixels.
5 CONCLUSIONS
Calibration of active cameras has to overcome some
difficulties that are not present for fixed cameras, such
as solving calibration equations for telescopic lenses
or large focal lengths and the fact that the rotation cen-
ter of the PTZ camera is not co-located with the prin-
cipal point. The goal of this work has been to obtain a
calibration algorithm for PTZ cameras that improves
the precision of volumetric reconstruction algorithms
applied to a combination of fixed and PTZ camera im-
ages in our Smart Room. The principal features we
wanted were real-time availability of calibration pa-
rameters for all range of pan, tilt and zoom values,
with re-projection errors smaller than one pixel spac-
ing in order to have precise 3D volumetric reconstruc-
tion.
State of the art methods did not provide a solution for
these goals. Methods for static cameras use to fail
for large focal lengths and require large tables to store
calibration values for the pan-tilt-zoom range. Meth-
ods for active cameras were more adequate but pro-
vided a good solution for only a small range of pan
and tilt.
The presented algorithm is flexible in the sense that it
provides readily available calibration parameters for
any combination of pan, tilt, and zoom, with a small
re-projection error, even though it is slightly larger
than one pixel.
Some sources of error have been identified. Probably,
the most influential error source is the assumption of
a nearly constant 3D position of the principal point of
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
14

the camera with respect to the zoom when, in practice,
the focal length in the zoom range of the camera can
vary up to a few centimeters. The consideration of
constant lens distortion for the zoom range is not true
either, although its influence in the final results might
be insignificant.
Another possible source of error is the position of the
calibration pattern in the Smart Room. The Smart
Room has some predefined points, precisely mea-
sured to put the calibration pattern on according to
arbitrary coordinates. For each attempt to position
the calibration pattern at predefined 3D world coordi-
nates, there is an error of about 0.5cm in the physical
location, which is small considering the actual dimen-
sions of the Smart Room(4m × 5m), but still enough
to affect camera calibration results.
ACKNOWLEDGEMENTS
We want to thank to Jeff Mulligan for the ideas given
in the algorithm definition and to Albert Gil for the
support given for camera grabbing software.
REFERENCES
Agapito, L. d., Hayman, E., and Reid, I. (1999). Self-
calibration of a rotating camera with varying intrinsic
parameters. In Proc. 9th British Machine Vision Con-
ference, Southampton., pages 105–114.
Bouguet, J. Y. (2007). Camera calibration tool-
box for matlab. (Available for download from
http://www.vision.caltech.edu/bouguetj/calib doc).
Chen, Y.-S., Shih, S.-W., Hung, Y. P., and Fuh, C. S.
(2001). Simple and efficient method of calibrating a
motorized zoom lens. Image and Vision Computing,
19(14):1099–1110.
Davis, J. and Chen, X. (2003). Calibrating pan-tilt cameras
in wide-area surveillance networks. In Ninth IEEE
International Conference on Computer Vision, 2003.
Proceedings, number 1, pages 144–149.
EVI-Lib (2006). C++ library for controlling the serial in-
terface with sony color video cameras evi-d30, evi-
d70, evi-d100 (http://sourceforge.net/projects/evilib/).
http://sourceforge.net/projects/evilib/.
Hartley, R. I. and Zisserman, A. (2000). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, ISBN: 0521623049.
Heikkila, J. (2000). Geometric camera calibration using
circular control points. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 22(10):1066–
1077.
Huang, X., Gao, J., and Yang, R. (2007). Calibrating pan-
tilt cameras with telephoto lenses. In Computer Vision
- ACCV 2007, 8th Asian Conference on Computer Vi-
sion, pages I: 127–137, Tokyo, Japan.
Kim, N., Kim, I., and Kim, H. (2006). Video surveillance
using dynamic configuration of multiple active cam-
eras. In IEEE International Conference on Image Pro-
cessing (ICIP06), pages 1761–1764.
Li, M. and Lavest, J.-M. (1996). Some aspects of zoom
lens camera calibration. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 18(11):1105–
1110.
Lim, S. N., Elgammal, A., and Davis, L. S. (2003).
Image-based pan-tilt camera control in a multi-
camera surveillance environment. In Proceedings
International Conference on Multimedia and Expo
(ICME’03), volume 1, pages I–645–8.
Ruiz, A., L´opez-de Teruel, P. E., and Garc´ıa-Mateos, G.
(2002). A note on principal point estimability. In
16th International Conference on Pattern Recognition
(ICPR’02), volume 2, pages 304–307.
Senior, A., Hampapur, A., and Lu, M. (2005). Ac-
quiring multi-scale images by pan-tilt-zoom control
and automatic multi-camera calibration. In Seventh
IEEE Workshops on Application of Computer Vision
(WACV/MOTION’05), pages 433–438.
Sinha, S. and Pollefeys, M. (2004). Towards calibrating
a pan-tilt-zoom camera network. In OMNIVIS 2004,
ECCV Conference Workshop CD-rom proceedings.
Svoboda, T., Martinec, D., and Pajdla, T. (2005). A con-
venient multi-camera self-calibration for virtual envi-
ronments. PRESENCE: Teleoperators and Virtual En-
vironments, 14(4):407–422.
Tsai, . R. Y. (1987). A versatile camera calibration tech-
nique for high-accuracy 3d machine vision metrology
using off-the-shelf tv cameras and lenses. IEEE J. of
Robotics and Automation, RA-3(4):323–344.
Willson, R. G. (1994). Modeling and Calibration of Au-
tomated Zoom Lenses. PhD thesis, Carnegie Mellon
University, Pittsburgh, PA, USA.
Zhang, Z. (2000). A flexible new technique for camera cal-
ibration. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 22(11):1330–1334.
INDOOR PTZ CAMERA CALIBRATION WITH CONCURRENT PT AXES
15
