SUBJECTIVE DECISION MAKING IN STUDENTS’
ASSESSMENT USING TYPE-2 FUZZY LOGIC ADVISOR
M. A Owais
Computer Science & Engineering Department, King Fahd University of Petroleum and Minerals
Hafr Al-Batin College, P.O Box# 1803, Hafr Al-Batin, 31991, Saudi Arabia
mowais@kfupm.edu.sa
Keywords: Student Evaluation, Fuzzy Logic, Uncertainty, Cooperative Training, Senior/Capstone Project, Type-2 FLA.
Abstract: In this paper, we present and compare two-stage type-2 fuzzy logic advisor (FLA) to evaluate the students’
performance in domains where subjective decisions are made. We test our proposed model for evaluating
students’ performance in Computer Science Department in two domains namely cooperating training and
senior project assessment where we find these FLAs very useful and promising. In our proposed model, the
assessment criteria for different components of cooperative training and senior project are transformed into
linguistic labels and evaluation information is extracted into the form of IF-THEN rules from the experts.
These rules are modelled using FLS, which then is used as a fuzzy logic advisor (FLA) to make decisions
about students’ grades. The evaluator’s input for the system can be either singleton or non-singleton. Both
type-1 and type-2 fuzzy logic based models are implemented and compared with individual expert’s
evaluation.
1 INTRODUCTION
A student’s learning performance is measured by
some evaluation means in all sorts of teachings. A
student’s evaluation is the process by which all
relevant data about a student’s work are collected
and transformed into information for decision
making (Cooley and Lohnes, 1976). In most of the
cases, testing provides a measure of progression and
success of a student’s learning. To evaluate a
student’s performance, it is worthwhile to use a
number of different ways rather than relying on a
single formal exam (Donald et al., 1985). There are
various formal and informal ways of evaluation
including homework assignments, quizzes, projects,
reports, formal exams, class participation, team
activities, interviews, attendance, punctuality etc.
Whatever the method, it is good to record fairly
often how students are performing in each area.
Another important aspect to note is that whatever
method be used, the evaluation process should help
students develop their proficiency in a subject.
At undergraduate or associate degree level,
cooperative training and/or senior project are two
most important mechanisms (tools) to develop the
skills of a student. Cooperative (coop) training
provides an opportunity for students to integrate and
apply their academic learning with some real work
experience in industry. While completing a senior
project, generally a student develops some industrial
project or solves some related industrial problem
based on the techniques he/she learnt during his
academic career. In both of the above cases, a
student is exposed to the profession of his/her
subject area by working in the field or solving a real
problem for the industry. Normally, such a student is
evaluated through different means e.g. submission of
progress and final reports, on-site observation,
assessing the proposed design, final presentation etc
and marks are assigned for each of these activities.
These partial marks (results) are weighed up in some
way (using numbers or percentage) in order to
decide the final grade of a student for coop training.
However, we feel that the assessment in such
domains (i.e. observing student’s attitude towards
work, quality of work output, initiative and
creativity, presenting his work in final report and
presentation etc) is quite subjective and mostly
based on perception of an evaluator. The
conventional methods for evaluation usually do not
take into account the uncertainties in usage of words
for assessment. This gives us the motivation for
type-2 fuzzy set be used to model a word as it covers
the word uncertainties by using the concept of
footprint of uncertainty.
In this paper, an interval type-2 fuzzy set based
Fuzzy Logic Advisor (FLA) is presented to decide
the final grade of a student’s coop training. We also
compare type-2 and type-1 fuzzy logic models for
evaluating coop training. This paper is organized as
follows; in section 2 we describe background details
about coop training and related work. In section 3
our fuzzy logic model for evaluation is explained.
Section 4 presents experiments and results. The
paper is concluded in section 5 mentioning the
future work also.
2 BACKGROUND
2.1 Importance of Selected Domain
For assessing and improving students’ learning,
coop training and senior project are very important
tools. Recent report (Peter, 2008) shows that the
employers hold high regard for evaluation of senior
projects and coop training because these enhance
students’ knowledge and develop their skills to work
in real-world environment. Most of the employers
advise universities/colleges to focus resources in
assessing these components for improving students’
learning.
2.2 Cooperative Training/ Internship
Cooperative (coop) training is a planned and
supervised on-site training. It helps students to gain
job-related work experience and skills that assists
them in achieving their career goals. There are
different student activities that are monitored during
and after the coop training. Based on this
monitoring, final grades are assigned according to
the student’s performance in each activity. In
universities/colleges coop students are evaluated
using different means. We use following four means
to evaluate coop students at our college:
1. A student submits a number of progress
reports to his/her internal supervisor during
the coop training period.
2. A student is evaluated by his supervisor
(external) at work. In addition, internal
supervisor may also visit the student to
monitor his/her performance in the field.
3. A student submits a final report to the
university/college about his training.
4. A student presents his/her work in a
presentation to internal and/or external
supervisors, faculty members and other
students.
2.3 Senior/Capstone Project
Senior project gives students the experience of
tackling a realistic problem. The intent is to show
how to input theoretical knowledge gained into
practical use by starting from a word description of a
problem and proceeding through various design
phases to end up with a practical solution. The
project supervisor(s) guides the student in
conducting a feasibility study, preparation of
specifications, and the methodology for the design.
Detailed design and implementation of the project
are carried out followed by testing, debugging, and
documentation. Similar to the coop training, we use
four different means for evaluating a student’s work
during completing senior project. Except for the
second point where supervisor assesses a student’s
performance by evaluating design methodology,
complexity, level of achievement, quality of results
etc of his/her project, the rest of the means are same
as discussed in section 2.2 for coop training. Note
that these evaluation criteria are flexible and
generally based on policies from university or
college (while in some cases evaluation depends on
each individual).
After a number of years’ experience, we feel that
a perception-based evaluation model is more
suitable for assessment of coop training and senior
projects. We believe that the judgment for students’
training at work, report writing (literary quality,
quality of subject matter, formatting, structure etc.)
and presenting the work during presentation
(communication skills, organization etc.) are mostly
subjective rather than objective. It is difficult to
apply the objective methods to evaluate these
student activities. Also we found that supervisors
feel more comfortable while giving their judgment
in terms of words (Excellent, Very Good, and Good
etc.) than in numbers. To solve this problem, we
propose the use of fuzzy logic to model the students’
evaluation.
2.4 Fuzzy Logic
Fuzzy logic was first proposed and coined by Lotfi
A. Zadeh in 1965 (Zadeh, 1965). The main
motivation behind fuzzy logic was the existence of
imprecision and uncertainty in the measurement
process. Later, Zadeh also proposed the
methodology of computing with words (CW) in
which words are used in place of numbers for
computing and reasoning (Zadeh, 1973; Zadeh
1996). The concept of CW is very important in
human decision making systems as they employ
mostly word in making decisions and judgments.
CW involves a combination of natural language and
computation with fuzzy variables. It mimics the
perception-based decision making done by humans
in an environment of imprecision, uncertainty and
partial truth (Zadeh 1996; Zadeh 1999). The next
subsections describe some of the important concepts
related to fuzzy logic.
2.4.1 Linguistic Variables, Values and
Terms
In fuzzy logic, linguistic variables accepts linguistic
values which are words (linguistic terms) with
associated degrees of membership in the set.
Therefore, instead of considering length as a
numerical variable that assumes a numerical value of
1.72 meters, it is treated as a linguistic variable that
may assume, for example, linguistic values of “high”
with a degree of membership of 0.92, "short” with a
degree of 0.06, or "medium” with a degree of 0.7.
Linguistic variables accept values defined in their
term set - their set of linguistic terms. Linguistic
terms are subjective categories for the linguistic
variable. For example, for linguistic variable age, the
term set T(age) may be defined as follows:
T(age) = { "young", "not young", "not so young",
"very young", ..., "middle aged", "not middle aged",
..., "old", "not old", "very old", "more or less old",
"quite old", ..., "not very young and not very old", ...
}
2.4.2 Fuzzy Sets and Membership Functions
Each linguistic term is associated with a fuzzy set,
each of which has a defined membership function
(MF). Formally, a fuzzy set A in U is expressed as a
set of ordered pairs:
}|))(,{( UinxxxA
A
μ
=
In the above definition )(x
A
μ
is the membership
function, which provides the degree of membership
of
x
. This indicates the degree to which
x
belongs
in set A, where U is the universe of discourse. Let’s
illustrate these concepts using an example. Consider
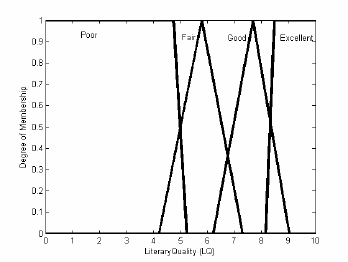
the “Literary Quality (LQ)” is a metric to measure
the how well a student writes his report in terms of
style, grammar, clarity etc. Figure 1 illustrates a
linguistic variable LQ with four associated linguistic
terms namely “Excellent”, “Good”, “Fair” and
“Poor”. Each of four linguistic terms is associated
with a fuzzy set defined by a corresponding
membership function.
There are many types of membership functions.
Some of the more common ones are triangular MFs,
trapezoidal MFs and Gaussian MFs.
2.4.3 Fuzzy Logic System
Fuzzy logic system is a system which has a direct
relationship with fuzzy concepts (such as fuzzy sets,
linguistic variables and so on) and fuzzy logic. The
most popular fuzzy logic systems in the literature
can be classified into three types: pure fuzzy logic
systems, Takagi and Sugeno’s fuzzy system, and
fuzzy logic system with fuzzifier and defuzzifier
(Wang, 1994).
Figure 1: Membership Functions for Literary Quality.
Since most of the engineering applications produce
crisp data as input and expects crisp data as output,
the last type is the most widely used one. Figure 2
shows the basic configuration of a fuzzy logic
system with fuzzifier and defuzzifier.
This type of fuzzy logic system was first
proposed by Mamdani (Mamdani, 1975). It has been
successfully applied to a variety of industrial
processes and consumer products (Mamdani, 1974).
The main fours components’ functions are as
follows.
Fuzzifier: It converts a crisp input to a fuzzy set.
Fuzzy Rule Base: Fuzzy logic systems use fuzzy
IF-THEN rules. A fuzzy IF-THEN rule is of the
form "IF X1 = A1 and X2 = A2 ... and Xn = An
THEN Y = B” where Xi and Y are linguistic
variables and Ai and B are linguistic terms. The ‘IF’
part is the antecedent or premise, while the ‘THEN’
part is the consequence or conclusion. An example
of a fuzzy IF-THEN rule is "IF Marks = Low THEN
Grade =Poor". In a fuzzy logic system, the collection
of fuzzy IF-THEN rules is stored in the fuzzy rule
base, which is known as the inference engine.
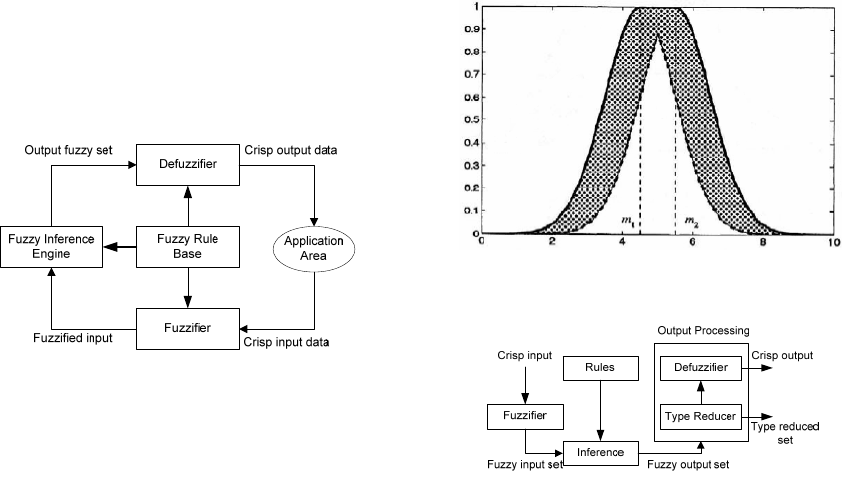
Fuzzy Inference Engine: Once all crisp input
values are fuzzified into their respective linguistic
values, the inference engine accesses the fuzzy rule
base to derive linguistic values for the intermediate
and the output linguistic variables. The inference
engine performs two main operations: aggregation
and composition. Aggregation is the process of
computing for the values of the IF (antecedent) part
of the rules while composition is the process of
computing for the values of the THEN (conclusion)
part of the rules.
Defuzzifier: It converts fuzzy output into crisp
output.
The details of the above four components can be
found in (Wang, 1994).
Figure 2: FLS with Fuzzifier and Defuzzifier.
Imprecise perception-based data can be best
modeled by using type-2 fuzzy logic (John and
Coupland, 2007). Mendel proposed using type-2
fuzzy sets and type-2 fuzzy logic systems to deal
with the different types of uncertainties (Mendel,
2001). Type-2 fuzzy sets help us to deal with the
uncertainty about the meaning of the words and
uncertainties about the consequent used in a rule.
Type-1 fuzzy sets cannot deal with this type of
uncertainty because the degree of membership is
considered as certain in type-1 fuzzy sets. Figure 3
shows footprint of uncertainty (FOU) for a Gaussian
membership function having a fixed standard
deviation, σ, and an uncertain mean that takes on
values in [m1, m2]. The example shown in Figure 3
depicts a case where the FOU is uniformly shaded. It
means that at each point in the FOU, the
membership degree is one. This type of membership
functions is known as interval type-2 membership
function.
A fuzzy logic system is considered to be type-2
as long as any one of its antecedent or consequent
sets is type-2. A detailed description of all the
components of Figure 4 and uncertain rule based
fuzzy logic (type-1 and type-2) system is provided
by Mendel (Mendel, 2001).
2.5 Related Work
Fuzzy theory has vast applications in different
disciplines from controls to machine learning to
decision making. It has also been applied in the
field of education (Ahmad, 2001; Kavcic et al.
2003). In (Montero et al., 2005), fuzzy logic based
evaluation system, to decide critical students’ final
marks, is presented. They used type-1 fuzzy logic
for evaluation purpose.
Figure 3: FOU for Gaussian Membership Function.
Figure 4: Type-2 Fuzzy Logic System.
In (Suarez, 2003), type-1 fuzzy set (membership
function) has been used to manage students’
performance in computer adaptive testing (CAT)
administration process. In (Zhou, 2001), criterion
referenced assessment techniques using fuzzy sets
(type-1) are proposed for student project assessment.
To our knowledge, type-2 fuzzy logic has not yet
been used for students’ evaluation, particularly for
coop training evaluation.
3 PROPOSED FUZZY LOGIC
ADVISOR
3.1 Assessment Components
As described in section 2.1, assessment of coop
training and senior project is divided into different
components. Each of these parts has number of
criteria to be monitored and evaluated during and
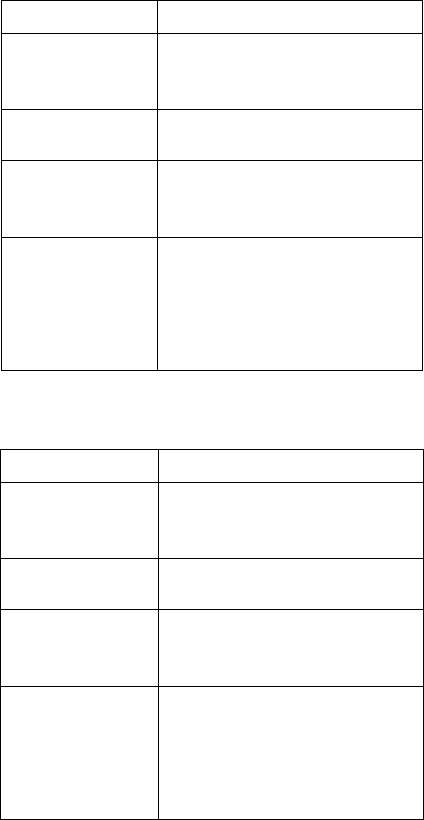
after training/project. Table 1 shows the four
different parts (means) of coop training evaluation
and their respective criteria to be judged by the
evaluator. Assessment components and criteria for
assessment for senior project are shown in Table 2.
The final grade of a student is computed based on
the outputs of four assessment components.
Table 1: Assessment Components and Criteria for Coop
Training.
Assessment
Component
Criteria for Assessment
Final Report
(FR)
• Format and Structure
• Literary Quality
• Quality of Subject Matter
Progress Report
(PR)
• Task Description
• Format and Submission
Final Presentation
(FP)
• Content and Organization
• Speaking (Presentation) Skills
• Response to Questions
External Evaluation
(EE)
• Enthusiasm and Interest in Work
• Ability to Learn and Search for
Information
• Relations with Co-Workers
• Punctuality and Delivering Work on
Time
Table 2: Assessment Components and Criteria for Senior
Project.
Assessment
Component
Criteria for Assessment
Final Report
(FR)
• Format and Structure
• Literary Quality
• Quality of Subject Matter
Progress Report
(PR)
• Task Description
• Format and Submission
Final Presentation
(FP)
• Content and Organization
• Speaking (Presentation) Skills
• Response to Questions
Supervisor Evaluation
(SE)
• Quality of Design Methodology and
Interest in Work
• Level of Achievement
• Quality of Results
• Punctuality and Delivering Work on
Time
3.2 Evaluation Model
We propose students’ coop and senior project
evaluation model based on knowledge mining
(knowledge engineering) methodology described in
(Mendel, 2001). The evaluation information is
extracted in the form of IF-THEN rules from
evaluators (experts) and these rules are modelled
using FLS, which then is used as a fuzzy logic
advisor (FLA) to make decisions about students’
grades. We propose a two-stage FLA based on
interval type-2 fuzzy logic, where each assessment
component is evaluated using an independent FLA
and then the results of these FLAs are combined to
calculate the final grade of a student using a second-
stage FLA. Figure 5 represents a two-stage FLA
framework for coop training. A similar model can be
drawn for senior project evaluation. Each of these
FLA has internal structure as described in section
2.2.4 (figure 4).
3.3 Antecedent & Consequent Fuzzy
Sets
In building a FLA we divide the whole range of all
the input (criteria of assessment) and output
(evaluation) attributes into number of fuzzy sets. We
use four type-2 fuzzy sets namely Excellent, Good,
Fair and Poor to represent each criterion of
assessment and the output of assessment
components of stage-1.
For our proposed model, we obtain this fuzzy set
classification from experts. As we have already
mentioned, different experts may provide different
assessments, based on their experience, regarding a
particular fuzzy set (e.g., Excellent) range of a
specific input/output attribute. This causes
uncertainty, as to which definition is more
appropriate to consider when one wants to define
antecedents/consequents while developing FLS. This
observation led us to use type-2 fuzzy sets, which
enables us to model uncertainty, caused due to
different experts’ opinion as just discussed, in the
FLS by blurring the antecedents’/consequents’
boundaries and defining the footprint of uncertainty
(FOU). For our model, based on survey from a
group of evaluators (experts) a range for above
labels is chosen using a scale 0 through 10. Table 3
shows the mean and standard deviation values for
these range labels based on our survey.
We associate triangle membership function with
the labels Fair (F) and Good (G), and piecewise
linear membership functions with labels Poor (P)
and Excellent (E). The uncertainty about the words
used in antecedents and consequents of rules and
uncertainties about the rule consequents are captured
in type-2 fuzzy sets using FOUs.
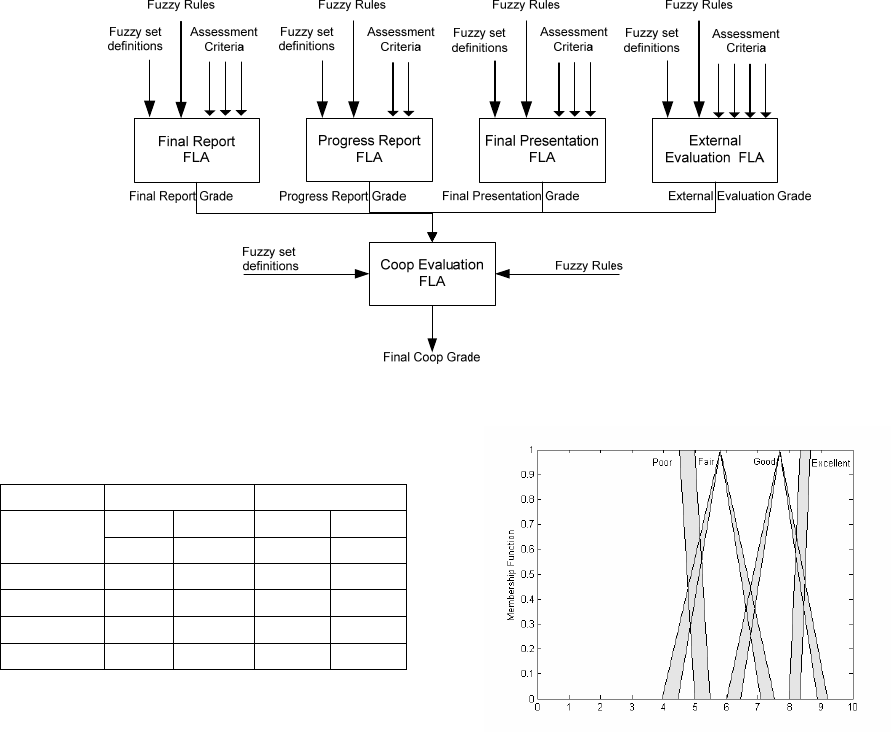
Figure 5: Two-Stage Type-2 Fuzzy Logic Based Framework for Cooperative Training Evaluation.
Table 3: Survey Results for Labels of Fuzzy Sets.
Label Mean Std. Deviation
Start End Start End
A b σ
a
σ
b
Poor
0 4.7389 0 0.4898
Fair
4.7056 6.8778 0.4978 0.4295
Good
6.6556 8.7222 0.4419 0.3153
Excellent
8.4889 10.0000 0.3296 0.0000
We obtain FOUs by specifying upper and lower
membership function for each fuzzy set. These
fuzzy sets are calculated based on procedure
described in (Mendel, 2001). Figure 6 shows the
FOUs for the four fuzzy sets for ρ=0.5 (50%
percent uncertainty), where ρ is the fraction of
uncertainty and
10 ≤≤
ρ
.
Similarly, for stage-2, the output of stage-1 will
be used as input in the form of type-2 fuzzy set
shown above. The output of stage-2 (Grade) is also
divided into nine different fuzzy sets namely
Exceptional, Excellent, Superior, Very Good,
Above Average, Good, High Pass, Pass, and Fail.
In our proposed model, the initialization of
membership functions is done through singleton
input.
The criteria of assessment (indicators of
assessment components) are represented by type-2
fuzzy sets as we believe that these criteria are
judged on the basis of perception of an evaluator.
Figure 6: FOUs for Linguistic Labels.
3.3 Fuzzy Rule Base and
Defuzzification
In the rules formulation we follow the approach
where all the possible combinations of antecedent
fuzzy sets are employed (Mendel 2001). The
consequents of rules are provided by the experts
(evaluators) through survey. Each rule has a
histogram of responses. Our proposed model is
composed of five FLAs and each one has its own
set of rules. The number of rules depends on the
number of inputs and fuzzy sets associated with
them.
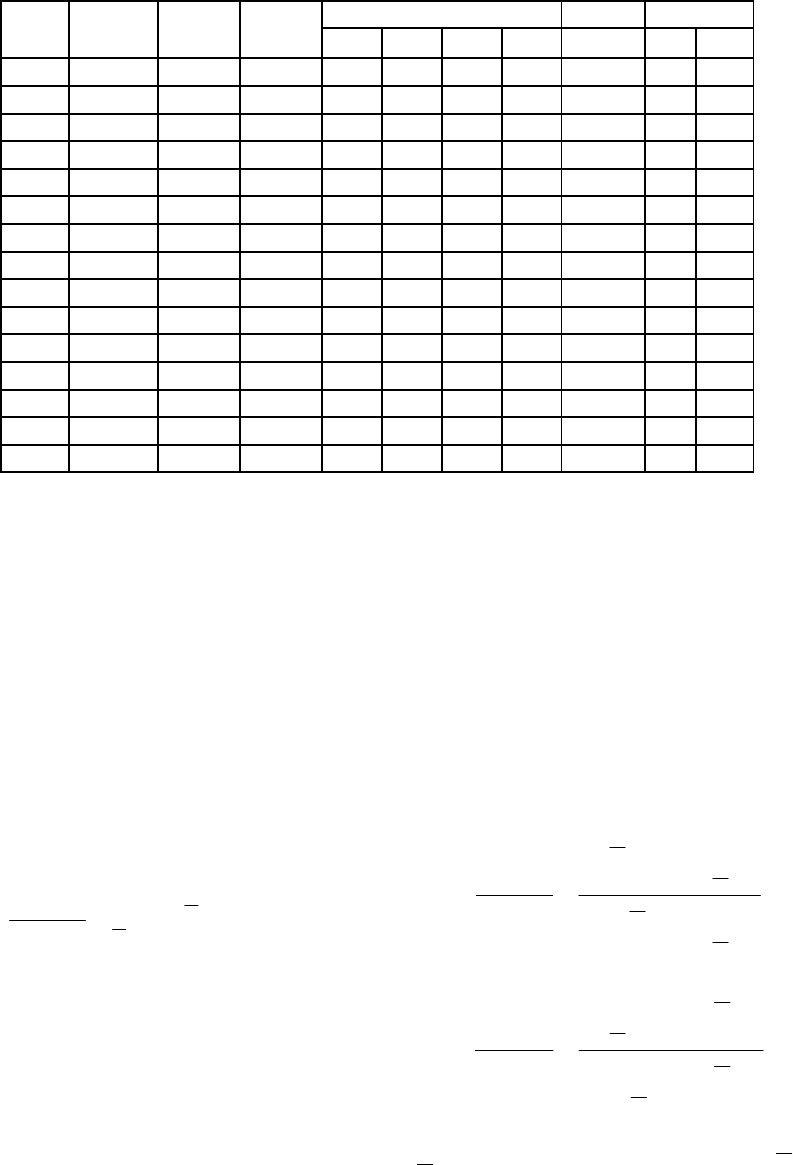
Table 4: Partial Histogram of Survey Responses for Final Report Evaluation.
Consequent Type-1 Type-2
Rule
No.
Antec. 1 Antec. 2 Antec. 3
Exc. Good Fair Poor C
avg
C
l
avg
C
r
avg
1 Excellent Excellent Excellent 8 0 0 0 9.162 9.08 9.24
2 Excellent Excellent Good 6 2 0 0 8.783 8.69 8.87
3 Excellent Excellent Fair 4 3 1 0 8.17 8.06 8.28
4 Excellent Excellent Poor 0 5 2 1 6.533 6.4 6.67
5 Excellent Good Excellent 6 2 0 0 8.783 8.69 8.87
6 Excellent Good Good 3 4 1 0 7.98 7.87 8.09
7 Excellent Good Fair 0 5 3 0 6.943 6.81 7.08
8 Excellent Good Poor 0 4 3 1 6.298 6.16 6.44
9 Excellent Fair Excellent 2 5 1 0 7.791 7.67 7.91
10 Excellent Fair Good 0 6 2 0 7.178 7.04 7.31
11 Excellent Fair Fair 0 5 3 0 6.943 6.81 7.08
12 Excellent Fair Poor 0 2 5 1 5.829 5.69 5.97
13 Excellent Poor Excellent 0 3 4 1 6.064 5.92 6.2
14 Excellent Poor Good 0 3 4 1 6.064 5.92 6.2
15 Excellent Poor Fair 0 0 6 2 4.95 4.8 5.1
For example, for Progress Report FLA, the number
of rules will be 4x4=16.While for Final Report
FLA, there will be 64 rules. Maximum number of
rules will be for External Evaluation FLA and
Coop Evaluation FLA i.e. 256. An example rule
for Coop Evaluation FLA will be of following
form:
Rl: IF FR is
E
~
AND PR is G
~
AND FP F
~
is
AND EE is
E
~
THEN GRADE is
DGV
~
(VERY
GOOD)
For later calculations, we find weighted
average (
l
avg
C ) of the rule consequents of each
rule using following formula (Mendel, 2001):
[]
l
avg
l
avg
M
i
l
i
M
i
iG
l
i
l
avg
CC
w
Cw
C ≡=
∑
∑
=
=
1
1
~
(1)
In the above equation,
iG
C
~
is the centroid of
the ith consequent and
l
i
w
is the weight associated
with the ith consequent for the lth rule. The
centroid for type-2 fuzzy sets is calculated using
the iterative procedure of the Karnik-Mendel (KM)
algorithm (Karnik and Mendel, 2001). The
consequent of each rule is treated as type-1 fuzzy
set. Initially we did survey for small group of
experts due to large number of rules. A partial
histogram of final report evaluation FLA with
three antecedents and a consequent, and
corresponding weighted average response for both
type-1 and type-2 is shown in table 4.
The final output of our proposed FLAs is a
type-reduce interval set, having the following
form:
[
]
rlTR
yyY ,
=
(2)
Where
l
y and
r
y are computed using
following two fuzzy basis function (FBF)
expansions (Mendel, 2001):
∑∑
∑∑
∑
∑
=+=
=+=
=
=
+
+
==
L
i
M
Li
i
i
L
i
M
Li
i
l
i
i
l
i
M
i
i
l
M
i
i
l
i
l
l
ff
yfyf
f
yf
y
11
11
1
1
(3)
∑∑
∑∑
∑
∑
=+=
=+=
=
=
+
+
==
R
i
M
Ri
i
i
R
i
M
Ri
i
r
i
i
r
i
M
i
i
r
M
i
i
r
i
r
r
ff
yfyf
f
yf
y
11
11
1
1
(4)
For a type-2 fuzzy set
F
~
, we calculate f and
f using following equations:
[
]
M
FFF
f
~
2
~
1
~
......,min
μ
μ
μ
=
(5)
[
]
M
FFF
f
~
2
~
1
~
......,min
μμμ
=
(6)
2
rl
yy
y
+
=
(7)
Finally, the defuzzified output of FLAs can be
found by using following equation:
4 EXPERIMENTS & RESULTS
We implemented type-1 and type-2 fuzzy logic
advisors (FLAs) using MATLAB fuzzy logic tool
box. We compared our FLA with the existing
coop/senior project evaluation system. In the
existing system, same assessment components are
used for coop evaluation but the usage of linguistic
labels with the range is fixed. Using these fixed
range assessment method, the overall performance
of a student is assessed by simply adding their
marks in different components. We implemented a
fuzzy logic advisor based on the inputs of experts
for range of different linguistic variables for
evaluation (shown in table 3). Our system uses the
rule-based fuzzy inference system to calculate the
overall grade of a student which provides more
accurate evaluation of a student as compared to
existing method. We found that the uncertainties in
the representation of criteria for assessment
(linguistic variables) can be well taken into
account by using type-2 fuzzy sets.
For verification of our model, we selected a
sample of students’ evaluation and compared the
outputs of the individual’s FLA with the output of
our proposed consensus type-1 and type-2 FLAs.
For this purpose same assessment components and
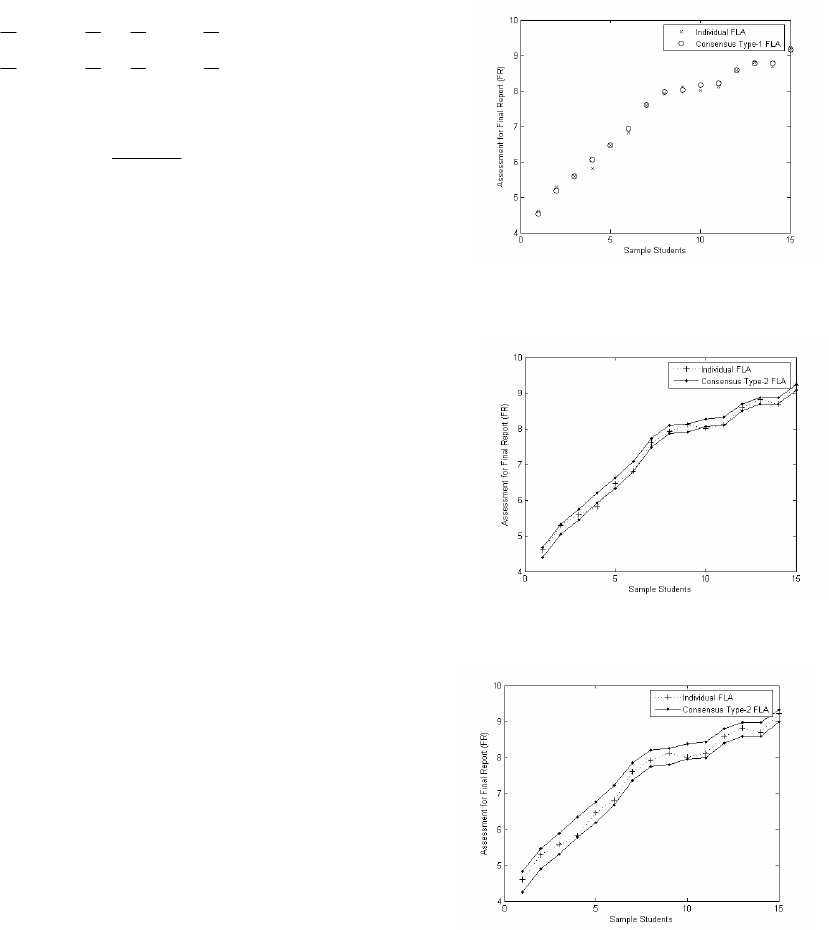
criteria were used. Figure 7 shows a comparison
for the outputs of individual and consensus type-1
FLAs for final report (FR) evaluation. This plot
shows that the outputs of individual and consensus
FLAs differ marginally for most of the students.
Figures 8 and 9 show the comparisons for
outputs of individual and consensus type-2 FLAs
for the same assessment component (FR) with 50%
and 100% uncertainty. These two plots depict that
the individual assessment lies in between the limits
of consensus assessment (left-hand and right-hand
curves) which reflects that type-2 based system
captures all those uncertainties which are there due
to words in surveys and consensus consequents.
Figure 7: Comparison for Individual and Type-1
Consensus.
Figure 8: Comparison for Individual and Type-2
Consensus FLAs (50% uncertainty).
Figure 9: Comparison for Individual and Type-2
Consensus FLAs (100% uncertainty).
5 CONCLUSIONS & FUTURE
WORK
This paper describes a rule-based fuzzy logic
advisor (FLA) to evaluate the cooperative training
and senior project of students at undergraduate and
associate degree level. We used the knowledge
mining (engineering) methodology to develop this
system where we gathered evaluation information
from experts. The system is initially tested for a
small group of students in computer science
department at our college and we found it very
useful for assessing students’ performance in their
cooperative training. Our type-2 fuzzy set model
has the potential to capture the uncertainties due to
words used in subjective evaluation of a student.
Future work involves further testing of the
system for large number of students from different
departments and investigating the use of the
system for other courses/situations e.g. assessing
group projects etc. Moreover, type-2 fuzzy sets
will also be tested for representing final grades.
There are some other issues which need to be
considered in future e.g. deciding the optimal
number of linguistic input/output variables for
assessment components, working with non-
singleton input from evaluators, and deciding the
appropriate number of experts for survey response
etc. In future these issues will be taken into
consideration for improving the overall
performance of the system.
REFERENCES
Ahamd, M. I. 2001. Assessment of Distance Education
Quality Using Fuzzy Sets Model. In the Proceedings
of International Conference on Engineering
Education, Oslo, Norway.
Cooley, W.W., AND Lohnes, P. 1976. Evaluation
Research in Education, Irvington Publishers, INC.,
New York.
Donald, J., Madsen, H., AND Hilferty A. 1985. TESOL:
Techniques and Procedures. Newbury House
Publisher.
John, R., Coupland, S. 2007. Type-2 Fuzzy Logic – A
Historical View. IEEE Computational Intelligence
Magazine. 2, 57-62.
Karnik, N. N., Mendel, J. M. 2001. Centroid of type-2
fuzzy sets, Information Sciences. 132, 195-220.
Kavic, A., Pedraza, R., Molina, H., Valverde, F., Cid, J.,
Navia, A. 2003. Student Modelling Based on Fuzzy
Inference Mechanisms. Proceedings of EUROCON,
Slovenia, 379-383.
Mamdani, E. H. 1974. Applications of Fuzzy Algorithms
for Simple Dynamic Plant, In the Proceedings of
IEEE. 121, 12, 1585-1588.
Mendel, J. M., Liang, Q. 1999. Pictorial Comparison of
Type-1 and Type-2 Fuzzy Logic Systems,
Proceedings of IASTED International Conference on
Intelligent Systems & Control, Santa Barbara, CA.
Mendel, J. M. 2001. Uncertain Rule-Based Fuzzy Logic
Systems, Prentice-Hall, Upper Saddle River, NJ
07458.
Montero, J. A., Alsina, R. M., Moran, J. A., Cid, M.
2005. Fuzzy Logic System for Students’ Evaluation,
Computational Intelligence and Bio-inspired
Systems, Lecture Notes in Computer Science. 3512,
1246-1253.
Wang, L. 1994. Adaptive Fuzzy System and Control:
Design and Stability Analysis. Prentice-Hall, Inc.,
Englewood Cliffs, New Jersey 07632.
Peter, D. H. 2008. How should colleges assess and
improve student learning? Liberal Education and
America’s Promise (Association of American
Colleges & Universities) - Report. January, 2008.
Suarez, J. 2003. Student Evaluation through
Membership Functions in CAT Systems. Revista
Mexicana De Fisica, 49, 371-378.
Zadeh, L. A. 1965. Fuzzy Sets, Information and Control.
8, 338-353.
Zadeh, L. A. 1973. Outline of a New Approach to the
analysis of Complex Systems and Decision Process,
IEEE Transaction. Syst., Man, Cybern. 3, 28-44.
Zadeh, L. A. 1975. The concept of a Linguistic Variable
and Its Application to Approximate Reasoning-I,
Information Sciences. 8, 199-249.
Zadeh, L. A. 1996. Fuzzy Logic = Computing with
Words, IEEE Transaction on Fuzzy Systems. 4, 103-
111.
Zadeh, L. A. 1999. Fuzzy Computing with Numbers to
Computing with Words – From Manipulation of
Measurements to Manipulation of Perceptions,
IEEE
Transaction on Circuits and Systems – I:
Fundamental Theory and Applications. 45, 105-119.
Zhou, D., Kwok, R.C.W., Zhang, Q., Ma, J. 2001. A
New Method for Student Project Assessment Using
Fuzzy Sets. 20th NAFIPS International Conference.
1, 25-28.
