
MULTI-CHIRP SIGNAL SEPARATION
B. Dugnol, C. Fern´andez, G. Galiano and J. Velasco
Dpto. de Matem´aticas, Universidad de Oviedo, c/ Calvo Sotelo s/n, 33007 Oviedo, Spain
Keywords:
Parametric model, Chirplet transform, Instantaneous frequency, Signal separation.
Abstract:
Assuming that an specific audio signal, such as recordings of animal sounds, may be modelled as an addition
of nonlinear chirps, we use the quadratic energy distribution corresponding to the Chirplet Transform of the
signal to produce estimates of the corresponding instantaneous frequencies, chirp-rates and amplitudes at each
instant of the recording and design an algorithm for tracking and separating the chirp components of the signal.
We demonstrate the accuracy of our algorithm applying it to some synthetic and field recorded signals.
1 INTRODUCTION
For many audio recordings obtained from natural
sources, such as emission from animals, it is a conve-
nient approach to use a parametric model in terms of
a super-position of chirps, s(t) =
∑
n
a
n
(t)exp[iφ
n
(t)],
with a
n
the analytic amplitude and φ
n
the phase,
whose derivative determines the chirp instantaneous
frequency (IF).
There are several techniques focused in the am-
plitude and phase estimation of this kind of sig-
nals. McAulay and Quartieri (McAulay and Quatieri,
1986) propose algorithms based on the STFT, while
for instance in (Maragos et al., 1993; Santhanam and
Maragos, 2000) these estimates are obtained through
the use of the Teager-Kaiser operator, E = (x
′
(t))
2
−
x(t)x
′′
(t). The IF estimation via non-parametric
models using Cohen distributions is also an impor-
tant issue, see, for instance, (Stankovi´c and Djurovi´c,
2003; Kwok and Jones, 2000; Zhao et al., 2004;
Boashash, 1992a; Boashash, 1992b).
Other kind of approaches, such as the empirical
mode decomposition (EMC) (et al., 1998)) or the Gi-
anfelici transform (Gianfelici et al., 2007) focus on
the signal decomposition in terms of basis which de-
pend on the given function.
In (Dugnol et al., 2008) we proposed a method-
ology based on the chirplet transform (Mann and
Haykin, 1991) to identify and separate the different
chirps conforming the given signal. To do this, not
only amplitude and IF estimation was needed but also
the so called chirp rate (CR, phase second derivative).
We showed that the quadratic energy corresponding
to the chirplet transform may be used for this task
since for each time of a discrete time mesh the max-
ima points of the energy in the IF-CR plane corre-
spond to some of the IF and CR of the existent chirps.
However, some other maxima are spurious maxima,
not corresponding to any chirp at all. Our previous
algorithm, see (Dugnol et al., 2008), had some ineffi-
ciencies regarding the identification of these spurious
maxima and, accordingly, to the matching process to
construct the global chirp components of the signal.
In this work we introduce important improvements to
our previous algorithm.
2 CHIRPLET TRANSFORM
ENERGY DISTRIBUTION
For a given signal f ∈ L
2
(R) we consider its chirplet
transform given by
Ψf (τ,ξ,µ;λ) =
Z
∞
−∞
f (t)
ψ
µ,λ
(t − τ)exp[−iξt]dt,
with τ,ξ and µ standing for time, IF and CR, respec-
tively, parameter λ determining the window width and
with ψ
µ,λ
a complex window defined as
ψ
µ,λ
(s) = v
λ
(s)exp
h
i
µ
2
s
2
i
,
with v
λ
(s) = λ
−1/2
v(s/λ) and v a non-negative, nor-
malized, symmetric window. The quadratic energy
corresponding to the chirplet transform is then given
by
P
ψ
f (τ,ξ, µ;λ) = |Ψf (τ,ξ,µ;λ)|
2
. (1)
216
Dugnol B., Fernández C., Galiano G. and Velasco J. (2009).
MULTI-CHIRP SIGNAL SEPARATION.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 216-221
DOI: 10.5220/0001432802160221
Copyright
c
SciTePress
We notice that Ψf may be rewritten as
Ψf (τ,ξ,µ,λ) =
Z
∞
−∞
f
′
(x)exp
h
−i
ξx+
µ
2
x
2
i
dx,
with f
′
(x) = f (x+ τ)v
λ
(x)exp[− iξτ], implying that
the Chirplet Transform provides a correlation mea-
sure of the linear chirp exp
−i
ξx+
µ
2
x
2
and the
portion of the signal centered at τ, . It is, then, clear
that for a linear chirp
f (t) = a
1
(t)exp
h
i
α
1
2
(t − τ)
2
+ β
1
(t − τ)+ γ
1
i
(2)
and for fixed τ and λ, the quadratic energy distribu-
tion P
Ψ
f(τ,ξ,µ;λ) has a global maximum at (ξ,µ) =
(α
1
,β
1
), allowing us to determine the IF and CR of
a given linear chirp at a fixed time by computing the
maximum point of the energy distribution. Moreover,
the following result holds, see (Dugnol et al., 2008):
For
f (t) = a(t)exp[iφ(t)] , (3)
and for all ε > 0 and ξ,µ ∈ R there exists L > 0 such
that if λ < L then
P
Ψ
f (τ,ξ,µ;λ) 6 λε+ P
Ψ
f
τ,φ
′
(τ),φ
′′
(τ);λ
. (4)
In addition,
lim
λ→0
1
λ
P
Ψ
f
τ,φ
′
(τ),φ
′′
(τ);λ
= a(τ)
2
. (5)
In other words, for a general mono-component chirp
the energy distribution maximum provides an arbi-
trarily close approximation to the IF and CR of the
signal. Moreover, its amplitude may also be estimated
by shrinking the window time support at the maxi-
mum point. In fact, these estimates make also pos-
sible to establish criteria for deciding, in the case of
a multi-chirp signal, when two energy maxima points
in the IF-CR plane do belong to the same chirp or to
different chirps, and in this way, it conforms a pro-
cedure for separating the chirp components (Dugnol
et al., 2008).
2.1 Energy Distribution in the CR-IF
Plane
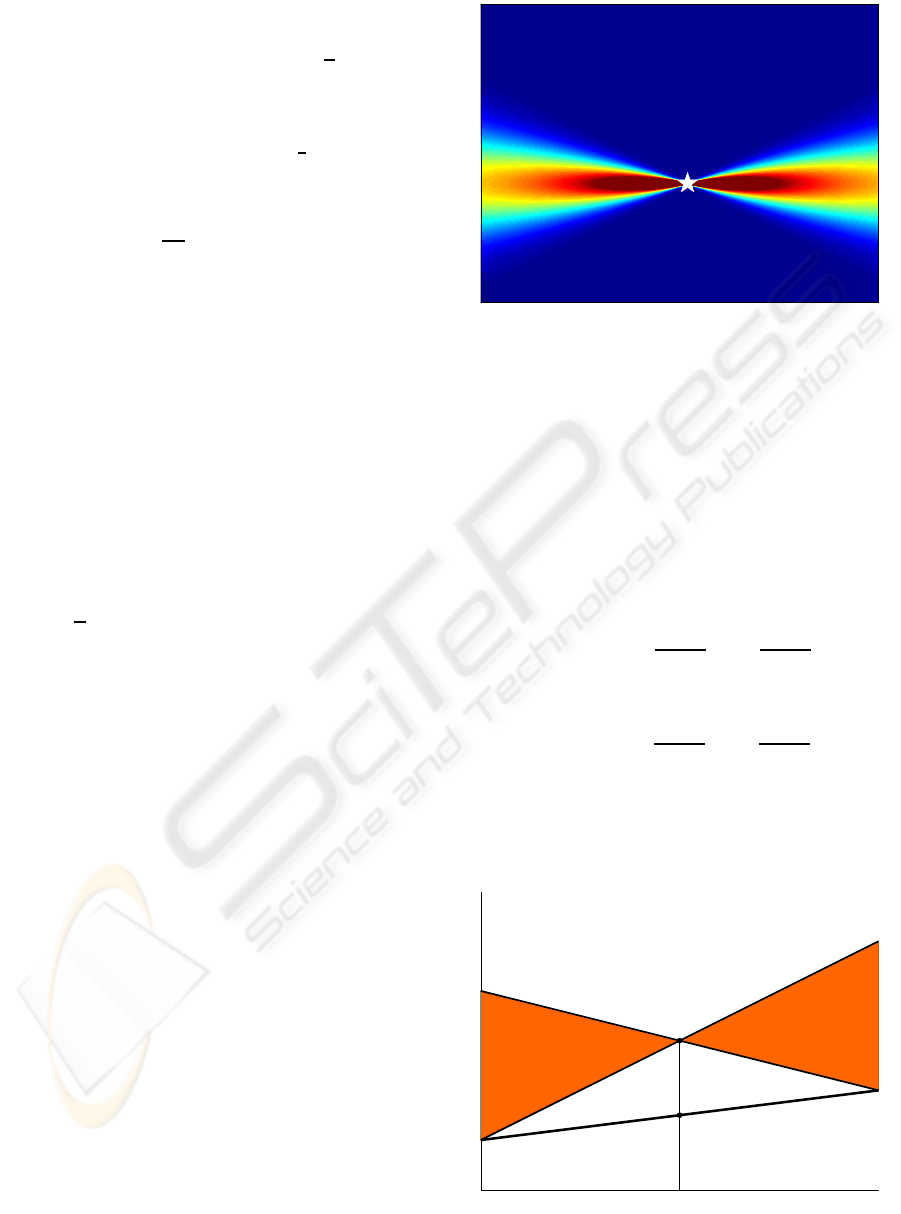
It may be experimentally observed that the support of
the energy distribution of a one-chirp signal like (3)
for a fixed time τ has a geometric shape given by a
double cone with vertex at (φ
′′
(τ),φ
′
(τ)) in the CR-
IF plane, see Figure 1.
Let us analyze the case of a linear chirp like (2) to
get some analytical insight into this property. By us-
ing an appropriate window we may restrict the anal-
ysis to the time interval (τ− λ,τ + λ). Fixing the ξ
value in the energy distribution (1) we obtain a line
I.F.
Chirp-rate
Figure 1: Energy distribution for one chirp signal at the CR-
IF plane.
bundle at (τ,ξ) generated by the different values of
the slope µ, see Fig. 2. For the energy distribution
to be remarkable, the segment defined in the time-
frequency plane by the chirp ω = α
1
(t − τ)+ β
1
must
intersect this bundle. Typically there exists a range
of slopes for which this intersection is not empty, see
Fig. 2. In particular, let r
ξ
(µ) = ξ + µ(t − τ) be the
line passing through (τ,ξ) with slope µ, and let
µ
m
:= min
α
1
+
ξ− β
1
λ
,α
1
−
ξ− β
1
λ
and
µ
M
:= max
α
1
+
ξ− β
1
λ
,α
1
−
ξ− β
1
λ
.
Then if µ ∈ (µ
m
,µ
M
), the segment r
ξ
(µ) = ξ+µ(t − τ)
does not intersect the chirp and therefore the energy
is negligible.
T ime
I.F.
(τ, ξ)
(τ, β
1
)
r
ξ
(µ
1,o
)
r
ξ
(µ
1,f
)
Figure 2: Shadow region corresponds to the chirplet negli-
gible energy set.
MULTI-CHIRP SIGNAL SEPARATION
217

T ime
Instantaneous frequency
ω = α
1
(t − τ) + β
1
r
µ
(ξ
1,0
)
r
µ
(ξ
1,f
)
Figure 3: Shadow region corresponds to the chirplet con-
centration energy set.
In a similar way, if we keep fixed the CR value
µ and move the IF value ξ we obtain that the en-
ergy is negligible outside an interval which depends
on the slopes µ,α
1
y α
2
, see Fig. 3. More precisely,
writing ξ
m
= min{β
1
+ λ(µ− α
1
),β
1
− λ(µ− α
1
)}
and ξ
M
= max{β
1
+ λ(µ− α
1
),β
1
− λ(µ− α
1
)}, we
have that the energy of the chirplet transform is con-
centrated in the interval (ξ
m
,ξ
M
).
Summarizing, for a one-chirp signal of the linear
form (2) we have that, for fixed time, its energy is con-
centrated in a region of the CR-IF plane of the form
(−∞,µ
m
(ξ))∪(µ
M
(ξ),+∞)×R ≡ R ×(ξ
m
(µ),ξ
M
(µ))
which illustrates de double cone shape in Fig. 1.
2.2 Spurious Maxima
For the more interesting case of a signal composed by
several chirps, the energy distribution will have max-
ima not only at ridge points but at the so called spuri-
ous maxima points. To understand this situation, we
consider a signal composed by two linear chirps
f (t) =
2
∑
k=1
a
k
(t)exp
h
i
α
k
2
(t − τ)
2
+ β
k
(t − τ)+ γ
k
]
Considering again a window centered at τ and of
width λ the time-frequency representation of the sig-
nal will be a pair of segments defined on the time
interval (τ− λ,τ + λ). If we keep constant the slope
value µ and move the IF value ξ, we see that the en-
ergy distribution will be negligible outside an interval
which depends on µ,α
1
y α
2
. Since the signal is com-
posed by two chirps, there arises a set S
2
in which
the segment r
µ
(ξ) intersects both chirps, a set S
1
in
which the segment intersects only one chirp and a set
S
0
with empty intersection, see Fig. 4, and therefore
where the energy is negligible.
T ime
Instantaneous frequency
ω = α
1
(t − τ ) + β
1
ω = α
2
(t − τ ) + β
2
S
1
S
1
S
0
S
2
S
0
Figure 4: Two chirps energy regions classification.
Since the instantaneous amplitudes are continu-
ous there exists a maximum point in the interval
[max{ξ
1,m
,ξ
2,m
},min{ξ
1,M
,ξ
2,M
}], which is not a
ridge point. It is a spurious maximum. We note that
these maxima do appear for large slope values and
IF’s localized between the IF’s of the corresponding
chirps at time τ.
3 CHIRP-TRACKING
Let us consider the multi-chirp signal
f (t) =
N
∑
k=1
a
k
(t)exp[iφ
k
(t)]
with φ
k
∈ C
3
, i.e., such that there exists M such that
φ
k
(t)
< M for k = 1, ...,N and for all t.
Assume that we know that at
τ,φ
k
(τ)
our signal
has a ridge point in the time-frequency plane and that
its CR is given by φ
k
(τ). Then, for h > 0 small we
have
φ
k
(τ+ h) = φ
k
(τ) + hφ
k
(τ) +
φ
k
(ν)
6
h
2
with ν ∈ (τ,τ+ h). From the regularity assumed on f
we deduce
φ
k
(τ+ h) − φ
k
(τ) − hφ
k
(τ)
6
1
6
Mh
2
.
Therefore, once we know the IF and CR at a given
time, we may estimate the range in which the CR will
be at the next time step.
On the other hand, we have
φ
k
(τ+ h) ≈ φ
k
(τ) + hφ
k
(τ)
i.e., φ
k
(τ+ h) ∈
φ
k
(τ) − hM,φ
k
(τ) + hM
. There-
fore, we may also estimate the range of slopes for the
CR at subsequent times.
Our algorithm is organized as follows:
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
218
1. We use a the signal spectrogram to choose the
time components of points at which the spectro-
gram has maxima, t = τ
1
,...,τ
L
. These are candi-
dates to belong to the support of the α
k
functions.
2. For each τ
l
we compute the chirplet energy distri-
bution corresponding to Ψf (τ
l
,ξ,µ;λ) for a dis-
crete set of slopes, µ
1
,...,µ
r
, using the DFT.
3. We compute the maximum of the energy obtain-
ing an estimate of the CR and IF (µ
l
0,1
,ξ
l
0,1
) of one
chirp at the given time.
4. We advance one step in time and compute the en-
ergy at τ
l
+ h.
5. To avoid spurious maxima, we seek the maximum
through the window estimated in the previous sec-
tion, i.e.
µ ∈ (µ
l
0,1
− hM,µ
l
0,1
+ hM)
and
ξ ∈
ξ
l
0,1
+ hµ
l
0,1
−
1
6
Mh
2
,ξ
l
0,1
+ hµ
l
0,1
+
1
6
Mh
2
This maximum provides us with an estimate for
the CR and IF, (µ
l
1,1
,ξ
l
1,1
).
6. We continue this process until the energy maxi-
mum in the selected window is lower than some
fixed threshold. In this way, we obtain a set of
ridge points corresponding to the same chirp.
7. We iterate steps 2-6 on every point computed at
step 1, until all the chirps of signal f are identified.
We finally notice that this new algorithm narrows the
search area for maxima points in the CR-IF plane, im-
plying a gain in computational time as well as a reduc-
tion in the spurious maxima processing.
4 NUMERICAL EXPERIMENTS
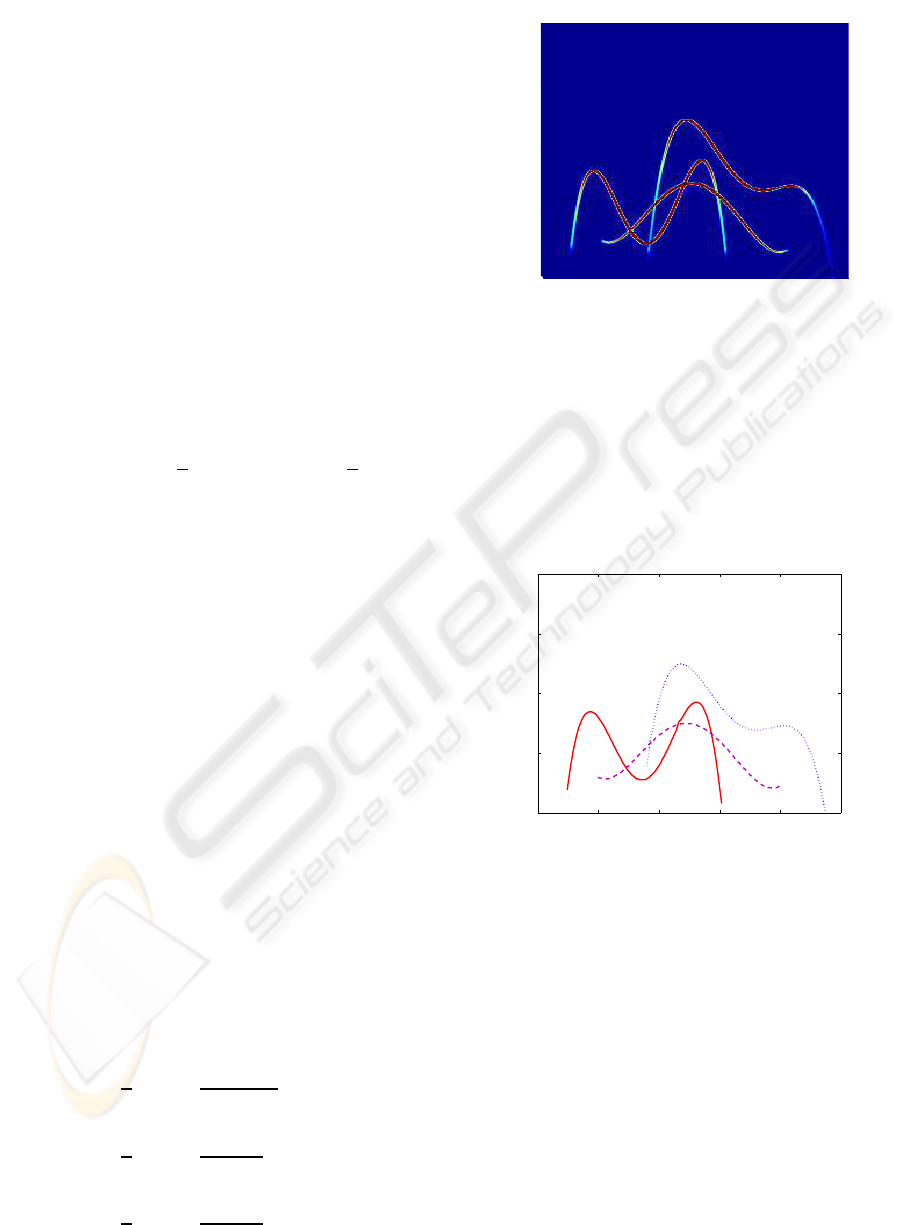
4.1 Experiment 1. A Synthetic Signal
We consider a synthetic signal composed by
the addition of three chirps (see Fig.5) f (t) =
∑
3
i=1
a
i
(t)cos[φ
i
(t)] with t ∈ [0, 10] and with ampli-
tudes given by amplitudes
a
1
(t) =
1
3
exp
−
(t − 3.5)
2
5
!
X
[1,6]
(t),
a
2
(t) =
1
3
exp
−
(t − 5)
2
4
!
X
[2,8]
(t),
a
3
(t) =
1
3
exp
−
(t − 6)
2
4
!
X
[3.5,9.5]
(t),
0 2 4 6 8
0
500
1000
1500
2000
Time
Frequency
Spectrogram
Figure 5: Spectrogram of synthetic signal of Experiment 1.
with X
[a,b]
(t) the characteristic function of the interval
[a,b], and with phases
φ
1
(t) = −13.07t
5
+ 226.2t
4
− 1434t
3
+ 4055t
2
− 4408t,
φ
2
(t) = 1.733t
5
− 42.92t
4
381.1t
3
− 1459t
2
+ 2798t,
φ
3
(t) = −4.973t
5
+ 166.3t
4
− 2172t
3
+ 0.138t
2
+ 0.411t.
0 2 4 6 8 10
0
500
1000
1500
2000
Time
Frequency
Separation
Figure 6: Separation of the three chirps of Experiment 1.
We used a variable time step h ∈ (0.01,0.05) sec.
The initial step is 0.01 sec. and in subsequent it-
erations we use h = 0.01c + 0.05(1 − c) with c =
min(|µ|,1000)/1000, for µ the CR estimation of the
previous step. Finally, we neglect maxima with am-
plitude lower than 0.001. Relative error results for
amplitude, IF and CR are plotted in Figs. 9, 10 and
11. We observe that, specially the IF, is very accu-
rately approximated, allowing the separation of the
three chirps, see Fig. 6. In a further experiment not
shown in this paper, we repeated the previous experi-
ment adding a noise to the signal with SNR=0. In this
case, the amplitude threshold was set to 0.025 and the
relative error results were very similar to those exhib-
ited by Figs. 9-11.
MULTI-CHIRP SIGNAL SEPARATION
219
0 0.5 1 1.5 2
0
500
1000
1500
2000
Time
Frequency
Spectrogram
Figure 7: Signal spectrogram corresponding to Experiment
2.
0 0.5 1 1.5 2
0
500
1000
1500
2000
Time
Frequency
Separation
Chirp 8
Chirp 7
Chirp 4
Chirp 6
Chirp 3
Chirp 1
Chirp 5
Chirp 2
Figure 8: Separation result corresponding to Experiment 2.
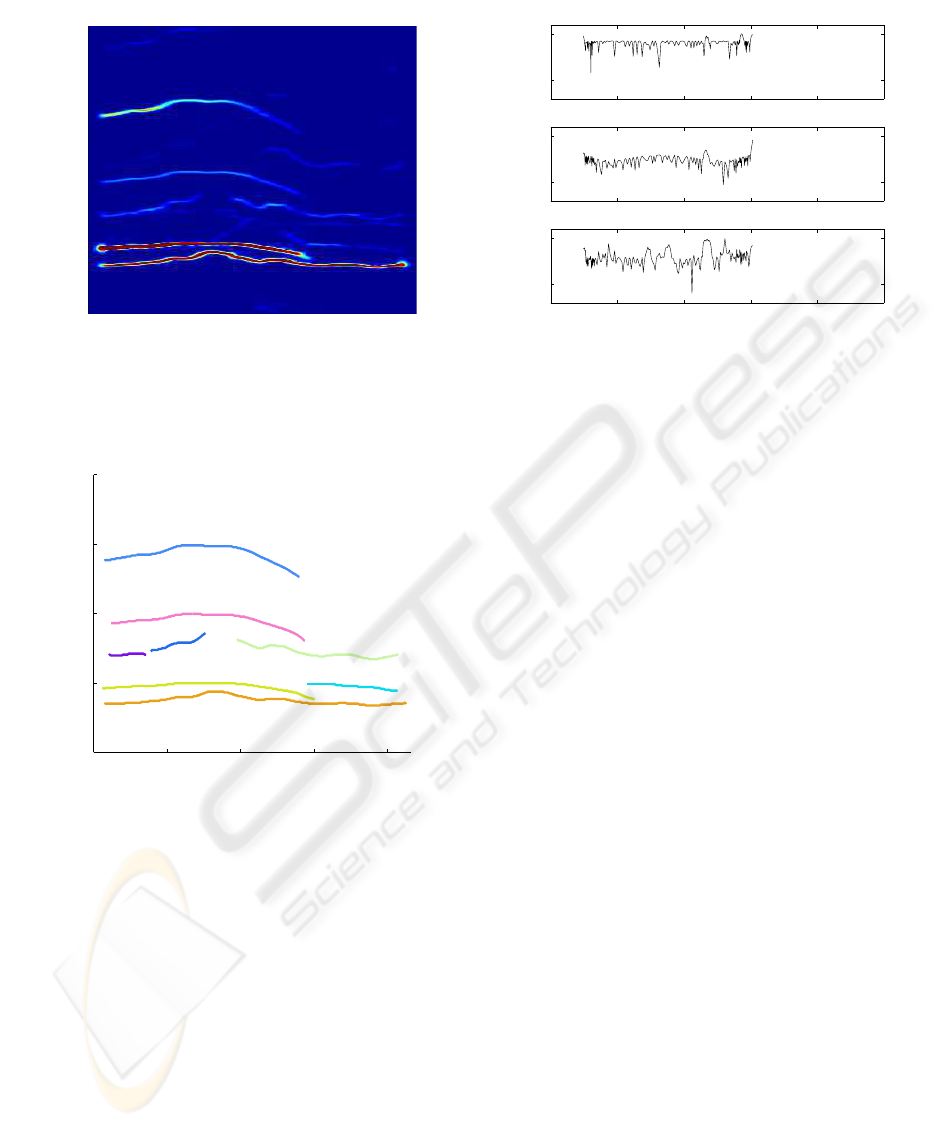
4.2 Experiment 2. A Field Recorded
Wolves Chorus
We use a wolf chorus field recorded signal. Parame-
ters are set as follows: window width, λ = 0.15, time
step h ∈ (0.001,0.005) sec. and the amplitude thresh-
old to 0.006. Fig. 7 shows the signal spectrogram
while Fig. 8 shows the separation result.
In Fig. 8 we observe the detection of eight chirps.
Due to the threshold level election some chirps are
split into several pieces due to the usual variation in
the amplitude of wolf howls, e. g. chirps 4, 5 and 6
in Fig. 8. However, if we consider a lower amplitude
threshold, the noise present in the recording induces
the erroneous identification of some points as ridge
0 2 4 6 8 10
1e−5
1e0
Amp.
Chirp 1
0 2 4 6 8 10
1e−5
1e0
F.I.
0 2 4 6 8 10
1e−5
1e0
Chirp-rate
Figure 9: Relative errors for chirp 1 of Experiment 1.
points. Hence, a suitable threshold level must be set
to balance these effects.
5 CONCLUSIONS
Many biological audio signals may be modelled as an
addition of modulated chirps being a problem of in-
terest the separation or decomposition of the signal in
its fundamental components. For this separation, spe-
cially at chirps crossing points in the time-frequency
plane, some additional information to instantaneous
frequency is needed in order to track correctly the dif-
ferent components. In a previous work, we introduced
an algorithm using the chirp-rate estimation based on
the chirplet transform. Some drawbacks of this al-
gorithm were the difficulties for defining an accurate
matching algorithm for the chirp segments computed
in each time step and the accuracy on the chirp-rate
computation, specially in which respects to the de-
tection of spurious maxima. In this paper we pre-
sented an improved algorithm which avoids the previ-
ous matching algorithm by means of a straight chirp
tracking procedure, based on an improved methodol-
ogy for energy maxima detection and spurious max-
ima identification.
ACKNOWLEDGEMENTS
All authors are supported by Project PC07-12, Gob-
ierno del Principado de Asturias, Spain. Third and
fourth authors are supported by the Spanish DGI
Project MTM2007-65088.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
220

0 2 4 6 8 10
1e−5
1e0
Amp.
Chirp 2
0 2 4 6 8 10
1e−5
1e0
F.I.
0 2 4 6 8 10
1e−5
1e0
Chirp-rate
Figure 10: Relative errors for chirp 2 of Experiment 1.
0 2 4 6 8 10
1e0
1e−5
Amp.
Chirp 3
0 2 4 6 8 10
1e0
1e−5
F.I.
0 2 4 6 8 10
1e0
1e−5
Chirp-rate
Figure 11: Relative errors for chirp 3 of Experiment 1.
REFERENCES
Boashash, B. (1992a). Estimating and interpreting the in-
stantaneous frequency of a signal. i. fundamentals.
Proceedings of the IEEE, 80(4):520–538.
Boashash, B. (1992b). Estimating and interpreting the in-
stantaneous frequency of asignal. ii. algorithms and
applications. Proceedings of the IEEE, 80(4):540–
568.
Dugnol, B., Fern´andez, C., Galiano, G., and Velasco, J.
(2008). On a chirplet transform based method applied
to separating and counting wolf howls. Signal Proc.,
88(7):1817–1826.
et al., N. E. H. (1998). The empirical mode decomposi-
tion and the hilbert spectrum for nonlinear and non-
stationary time series analysis. Proc. R. Soc. London
A, 454(1971):903–995.
Gianfelici, F., Biagetti, G., Crippa, P., and Turchetti, C.
(2007). Multicomponent am-fm representations: An
asymptotically exact approach. IEEE Trans. Audio
Speech Lang. Process., 15(3):823–837.
Kwok, H. and Jones, D. (2000). Improved instanta-
neous frequency estimation using an adaptive short-
time fourier transform. IEEE Trans. Signal Process.,
48(10):2964–2972.
Mann, S. and Haykin, S. (1991). The chirplet transform:
A generalization of gabor’s logon transform. In Proc.
Vision Interface 1991, pages 205–212.
Maragos, P., Kaiser, J. F., and Quatieri, T. F. (1993). Energy
separation in signal modulations with applications to
speech analysis. IEEE Trans. Speech Audio Process.,
41(10):3024–3051.
McAulay, R. J. and Quatieri, T. F. (1986). Speech
analysis/synthesis based on a sinusoidal representa-
tion. IEEE Trans. Acoustics Speech Signal Process.,
34(4):744–754.
Santhanam, B. and Maragos, P. (2000). Multicomponent
am-fm demodulation via periodicity-based algebraic
separation and energy-based demodulation. IEEE
Trans. Commun., 48(3):473–490.
Stankovi´c, L. and Djurovi´c, I. (2003). Instantaneous fre-
quency estimation by using the wigner distribution
and linear interpolation. Signal Process., 83(3):483–
491.
Zhao, Z., Pan, M., and Chen, Y. (2004). Instantaneous fre-
quency estimate for non-stationary signal. In Fifth
World Congress on Intelligent Control and Automa-
tion, 2004. WCICA 2004., volume 4, pages 3641–
3643.
MULTI-CHIRP SIGNAL SEPARATION
221
