
ARRAY-BASED GENOME COMPARISON OF ARABIDOPSIS
ECOTYPES USING HIDDEN MARKOV MODELS
Michael Seifert
1
, Ali Banaei
1
, Jens Keilwagen
1
, Michael Florian Mette
1
, Andreas Houben
1
Franc¸ois Roudier
2
, Vincent Colot
2
, Ivo Grosse
3
and Marc Strickert
1
1
Leibniz Institute of Plant Genetics and Crop Plant Research, Corrensstr. 3, 06466 Gatersleben, Germany
2
Ecole Normale Sup
´
erieure, D
´
epartement de Biologie, CNRS UMR8186, 46 rue d’Ulm, 75230 Paris cedex 05, France
3
Martin Luther University, Institute of Computer Science, Von-Seckendorff-Platz 1, 06120 Halle, Germany
Keywords:
Array-CGH, Comparative Genomics, Arabidopsis Ecotypes, Hidden Markov Model(HMM).
Abstract:
Arabidopsis thaliana is an important model organism in plant biology with a broad geographic distribution
including ecotypes from Africa, America, Asia, and Europe. The natural variation of different ecotypes is
expected to be reflected to a substantial degree in their genome sequences. Array comparative genomic hy-
bridization (Array-CGH) can be used to quantify the natural variation of different ecotypes at the DNA level.
Besides, such Array-CGH data provides the basics to establish a genome-wide map of DNA copy number vari-
ation for different ecotypes. Here, we present a new approach based on Hidden Markov Models (HMMs) to
predict copy number variations in Array-CGH experiments. Using this approach, an improved genome-wide
characterization of DNA segments with decreased or increased copy numbers is obtained in comparison to the
routinely used segMNT algorithm. The software and the data set used in this case study can be downloaded
from http://dig.ipk-gatersleben.de/HMMs/ACGH/ACGH.html.
1 INTRODUCTION
The method of array-based comparative genomic hy-
bridization (Array-CGH) has been widely applied to
several genomes for studying deletions, insertions,
and amplifications of DNA segments (Mantripragada
et al., 2004) including studies on Arabidopsis thaliana
(Borevitz et al., 2003; Martienessen et al., 2005;
Fan et al., 2007) an important model organism in
plant biology. Due to the broad geographic distribu-
tion of Arabidopsis thaliana ecotypes their the natu-
ral variation is expected to be reflected to a substan-
tial degree in their genome sequences. The applica-
tion of Array-CGH to these genomes allows to quan-
tify the natural variation at the DNA level. The ob-
tained Array-CGH data provides basics to establish
a genome-wide map of DNA copy number variations
between different ecotypes. Based on such a map,
future studies of DNA-histone interactions, histone
modifications, or transcript profiling will allow an im-
proved comparison of different ecotypes.
One important bioinformatics tasks is to cre-
ate a genome-wide map characterizing regions of
DNA copy number variations in Array-CGH data
of different ecotypes. In recent years, the pre-
diction of DNA copy number variations in tumor
data has received most attention, leading to the de-
velopment of many different approaches for deter-
mining copy number variations in Array-CGH data.
These approaches include genetic local search algo-
rithms (Jong et al., 2004), adaptive weights smooth-
ing, (Hup
´
e et al., 2004), and Hidden Markov Models
(HMMs) (Fridlyand et al., 2004; Marioni et al., 2006;
Cahan et al., 2008). Contributions to the comparison
of different approaches have been made by two recent
studies (Lai et al., 2005; Willenbrock and Fridlyand,
2005).
The basic concept of applying HMMs to the anal-
ysis of Array-CGH data was initially developed by
(Fridlyand et al., 2004). In this paper, we propose
a new method based on HMMs for the detection
of DNA segments with decreased or increased copy
numbers from Array-CGH data. This approach has
the following features: (i) we use a three-state HMM
partitioning DNA segments into segments of de-
creased, unchanged, or increased copy numbers, (ii)
we incorporate a priori knowledge into the training
of the HMM, and (iii) we use permuted Array-CGH
data to score predicted DNA segments with decreased
or increased copy numbers. We apply this HMM ap-
3
Seifert M., Banaei A., Keilwagen J., Mette M., Houben A., Roudier F., Colot V., Grosse I. and Strickert M. (2009).
ARRAY-BASED GENOME COMPARISON OF ARABIDOPSIS ECOTYPES USING HIDDEN MARKOV MODELS.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 3-11
DOI: 10.5220/0001123700030011
Copyright
c
SciTePress
proach to Array-CGH data of Arabidopsis thaliana
ecotypes from whole-genome NimbleGen tiling ar-
rays. We obtain an improved genome-wide map of
copy number variations compared to the standard
segMNT algorithm (Roche NimbleGen, Inc., 2008)
routinely used for this task.
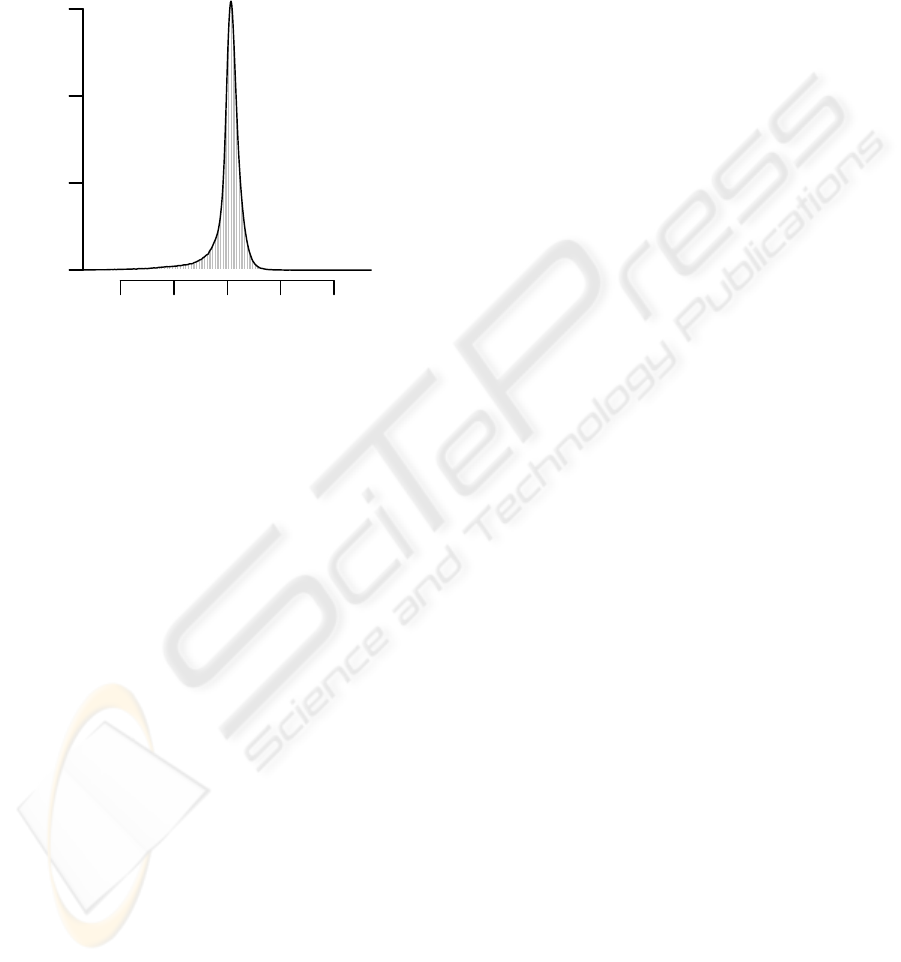
Density
−4 −2 0 2 4
0.0
0.5
1.0
1.5
Log−Ratio
Density
Figure 1: Histogram of log-ratios for Arabidopsis thaliana
ecotype C24 versus ecotype Columbia. The majority of log-
ratios is located at about zero, indicating that the majority
of DNA segments have not changed their copy numbers in
C24 compared to Columbia. Additionally, the proportion
of log-ratios in the negative tail is significantly higher than
the proportion of log-ratios in the positive tail. That is, we
expect to find more DNA segments with decreased copy
numbers in C24 than segments with increased copy num-
bers. The main reason for the asymmetry of the log-ratio
distribution is that DNA segments which are deleted in the
genome of Columbia, but which are present in the genome
of C24 cannot be measured using a tiling array representing
the reference genome of Columbia.
2 METHODS
2.1 Array-CGH Data
For the Array-CGH-based genome comparison of
Arabidopsis thaliana ecotypes C24 and Columbia,
leaf tissue is used to extract the DNA. Then the DNA
is sheared by sonication and resulting DNA segments
are differentially color-labeled for each ecotype. Sub-
sequently, these DNA segments are hybridized to
NimbleGen tiling arrays representing the reference
genome of ecotype Columbia. The arrays are read
out and further processed using the NimbleScan soft-
ware (Roche NimbleGen, Inc.) resulting in normal-
ized log-ratios o
t
= log
2
(I
t
(C24)/I
t
(Columbia)) for
all tiles t of an array, where I
t
(C24) and I
t
(Columbia)
are the intensities of tile t under the corresponding
ecotype. Based on information about the chromo-
somal locations of all tiles of an array, we create an
Array-CGH profile o = o
1
,...,o
T
for each chromo-
some where all log-ratios o
t
are represented in in-
creasing order of their chromosomal positions. Each
Array-CGH experiment consists of two independent
arrays with tiles at slightly different chromosomal lo-
cations. That is, for two adjacent tiles of a chromo-
some spotted on one array there generally exists one
tile on the other array having its chromosomal po-
sition between these first two tiles (interleaved de-
sign). The mean distance of two adjacent tiles on
a chromosome is about 350 bp for one array. The
length of hybridized segments is about 300 to 900
bp. Each array contains about 365,000 tiles that we
separate into K = 7 Array-CGH profiles o
1
,...,o
K
.
The first five profiles represent the chromosomes of
Arabidopsis thaliana and the last two contain the mea-
surements for chloroplastic and mitochondrial DNA.
We treat both arrays of an Array-CGH experiment in-
dependently to validate the reproducibility of our re-
sults. A histogram of log-ratios of the Array-CGH
data used in this case study is shown in Fig. 1.
2.2 HMM-based Data Analysis
2.2.1 HMM Description
We use a three-state HMM λ = (S,π,A,E) with Gaus-
sian emission densities for the genome-wide detection
of regional DNA copy number variations in Arabidop-
sis thaliana ecotypes. The basis of this HMM is the
set of states S = {−,=,+}. These states model the
copy number status of DNA regions in ecotype C24
that is compared to the reference genome of ecotype
Columbia. Thus, state − corresponds to DNA regions
with decreased copy number, state = corresponds to
DNA regions with unchanged copy number, and state
+ corresponds to DNA regions with increased copy
number. The state of tile t is denoted by q
t
∈ S. We
assume that a state sequence q = q
1
,...,q
T
belonging
to an Array-CGH profile o is generated by a homoge-
neous Markov model of order one with (i) start distri-
bution π = (π
−
,π
=
,π
+
), where π
i
denotes the prob-
ability that the first state q
1
is equal to i ∈ S, and (ii)
stochastic transition matrix
A =
a
−−
a
−=
a
−+
a
=−
a
==
a
=+
a
+−
a
+=
a
++
where a
i j
denotes the conditional probability that
state q
t+1
is equal to j ∈S given that state q
t
is equal to
i ∈S. Clearly, the start distribution fulfills
∑
i∈S
π
i
= 1,
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
4
and the transition probabilities of each state i ∈ S ful-
fill
∑
j∈S
a
i j
= 1. The state sequence is assumed to be
non-observable, i.e. hidden, and the log-ratio o
t
of tile
t is assumed to be drawn from a Gaussian emission
density, whose mean and standard deviation depend
on state q
t
. We denote the vector of emission parame-
ters by E = (µ
−
,µ
=
,µ
+
,σ
−
,σ
=
σ
+
) with mean µ
i
∈R
and standard deviation σ
i
∈R
+
for the Gaussian emis-
sion density
b
i
(o
t
) =
1
√
2πσ
i
exp
−
1
2
(o
t
−µ
i
)
2
σ
2
i
of log-ratio o
t
given state q
t
= i ∈ S. An illustra-
tion of the proposed HMM is given in Fig. 2. Since
we have nearly equidistant tiles along a chromosome
with distances about 350 bp for adjacent tiles, we do
not model chromosomal distances between adjacent
tiles. Approaches that explicitly take adjacent dis-
tances into account are e.g. BioHMM (Marioni et al.,
2006) and RJaCGH (Rueda and D
´
ıaz-Uriate, 2007).
2.2.2 HMM Initialization
In general, a good initial HMM should differentiate
DNA regions of decreased or increased copy numbers
from DNA regions of unchanged copy numbers with
respect to their log-ratios in the Array-CGH profile.
Hence, a histogram of log-ratios, like in Fig. 1, helps
to find good initial HMM parameters. The choice
of initial parameters addresses the two realistic pre-
sumptions. The first one is that the proportion of DNA
regions with unchanged copy numbers is much higher
than that of DNA regions of decreased or increased
copy numbers. The second presumption is that the
number of successive tiles with unchanged DNA copy
numbers is also much higher than the number of suc-
cessive tiles with decreased or increased DNA copy
numbers. In this case study, we use π
−
= 0.2, π
=
=
0.75, and π
+
= 0.05 resulting in an initial start dis-
tribution π = (0.2, 0.75, 0.05) where most weight is
given to the state representing tiles with unchanged
copy number. Based on that, we choose an initial tran-
sition matrix A with equilibrium distribution π. That
is, we set the self-transition probability of state i ∈ S
to a
ii
= 1 −s/π
i
with respect to the scale parameter
s = 0.025 to control the state durations, and we use
a
i j
= (1 −a
ii
)/2 for a transition from state i to state
j ∈S\{i}. We characterize the states by proper means
and standard deviations using initial emission param-
eters µ
−
= −2.5, µ
=
= 0, µ
+
= 1.5, σ
−
= 1, σ
=
= 1,
and σ
+
= 0.5. We refer to the initial HMM by λ
1
.
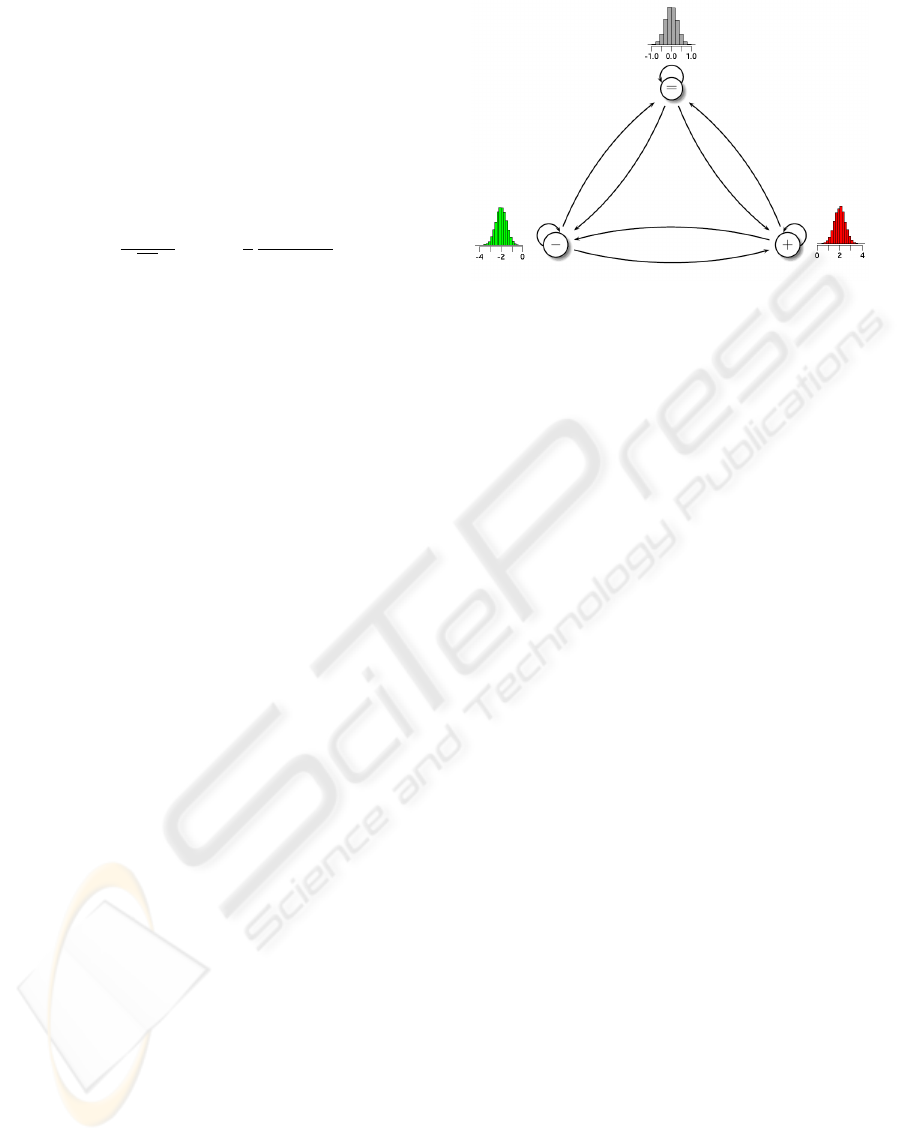
Figure 2: Three-state HMM with Gaussian emission densi-
ties for the analysis of Array-CGH data. States of the HMM
are represented by circles labeled with − (decreased), =
(unchanged), and + (increased) modeling copy numbers
of DNA segments in an ecotype compared to a reference
genome. Transitions between states are represented by ar-
rows modeling all possible transitions in an Array-CGH
profile. Gaussian emission densities characterize the states.
Thus, the emission density of the unchanged state (gray) has
its mean about zero, whereas the emission densities of the
decreased state (green) and the increased state (red) have
means significantly different from zero.
2.2.3 HMM Prior
The incorporation of a priori knowledge is of prime
importance for training an HMM to predict biologi-
cally relevant segments that vary in their copy num-
bers between ecotypes. This can be realized using a
prior distribution. We define the prior P[λ|Φ] of the
HMM λ as a product of independent priors for each
type of HMM parameters by
P[λ|Φ] = P[π|Φ] ·P[A|Φ] ·P[E|Φ].
We use a conjugate Dirichlet prior P[π|Φ] for start dis-
tribution π defined by
P[π|Φ] = c
π
∏
i∈S
π
ϑ
π
−1
i
with positive hyper-parameter ϑ
π
∈Φ and normaliza-
tion constant c
π
. The product of conjugate Dirichlet
priors P[A|Φ] for transition matrix A is given by
P[A|Φ] = c
A
∏
i∈S
∏
j∈S
a
ϑ
a
−1
i j
with positive hyper-parameter ϑ
a
∈Φ and normaliza-
tion constant c
A
. We realize the prior for emission
parameters E using a product of conjugate Normal-
Gamma priors
P[E|Φ] =
∏
i∈S
P[µ
i
|Φ] ·P[σ
i
|Φ]
ARRAY-BASED GENOME COMPARISON OF ARABIDOPSIS ECOTYPES USING HIDDEN MARKOV MODELS
5

consisting of a state specific Gaussian density
P[µ
i
|Φ] =
√
ε
i
√
2πσ
i
exp
−
ε
i
2
(µ
i
−η
i
)
2
σ
2
i
as prior for mean µ
i
with positive hyper-parameters
η
i
∈ Φ (a priori mean) and ε
i
∈ Φ (scale of a priori
mean), and a state-specific Inverted-Gamma prior
P[σ
i
|Φ] =
2α
r
i
i
Γ(r
i
)σ
2r
i
+1
i
exp
−
α
i
σ
2
i
as prior for the standard deviation σ
i
with posi-
tive hyper-parameters α
i
∈ Φ (scale of standard devi-
ation) and r
i
∈ Φ (shape of standard deviation). The
choice of this prior allows to include biological a pri-
ori knowledge into the training of the HMM. As mo-
tivated in Fig. 1, the integration of information about
the emission parameters of the HMM is important.
Additionally, the used prior allows to determine ana-
lytical parameter re-estimators for the HMM training.
Especially, with the choice of the Normal-Gamma
distribution as prior for a Gaussian emission density,
we follow (Richardson and Green, 1997) transform-
ing the proposed Gamma distribution as prior for the
precision σ
−2
i
into an Inverted-Gamma prior for the
standard deviation σ
i
. With respect to the underlying
biological question and motivated by the histogram
of log-ratios in Fig. 1, we set the parameters of the
Normal-Gamma priors to η
−
= −2.5, η
=
= 0, and
η
+
= 1.5 (a priori means). We use ε
−
= 10,000,
ε
=
= 1,000 and ε
+
= 7,500 (scale of a priori means),
r
−
= 20,000, r
=
= 1, and r
+
= 1,000 (shape of stan-
dard deviations), and α
−
= α
=
= α
+
= 10
−4
(scale
of standard deviations), but in general this depends
on the number of tiles in an Array-CGH experiment.
We ensure that the HMM can start in each state and
that all transitions are allowed by setting ϑ
π
= 10/3
and ϑ
a
= 10/9. The choice of these prior parameters
ensures a good characterization of the three HMM
states.
2.2.4 HMM Training
In most cases HMMs are trained by iteratively max-
imizing the likelihood of the observation sequences
under the model using the Baum-Welch algorithm
(Baum, 1972; Rabiner, 1989; Durbin et al., 1998).
This algorithm is part of the class of EM algorithms,
which can be extended to include a priori knowledge
into the iterative training by maximizing the posterior
(Dempster et al., 1977). We train the initial HMM
on all Array-CGH profiles using a maximum a pos-
teriori (MAP) variant of the standard Baum-Welch
algorithm. That is, we iteratively obtain new HMM
parameters
λ
h+1
= argmax
λ
Q(λ|λ
h
) + log (P[λ|Φ])
that maximize the posterior based on given
Array-CGH profiles O = (o
1
,...,o
K
) and cur-
rent HMM parameters λ
h
. Here, Q(λ|λ
h
) represents
Baum’s auxiliary function (Rabiner, 1989; Durbin
et al., 1998)
Q(λ|λ
h
) =
K
∑
k=1
∑
q∈S
T
k
P[q|o
k
,λ
h
]log
P[o
k
,q|λ]
with complete data likelihood
P[o,q|λ] = π
q
t
T −1
∏
t=1
a
q
t
q
t+1
T
∏
t=1
b
q
t
(o
t
)
of Array-CGH profile o and corresponding state
sequence q. The conflation of Q(λ|λ
h
) and P[λ|Φ] en-
ables us to include state-specific a priori knowledge
about the parameters of Gaussian emission densities
into the training. Based on that, we use Lagrange
multipliers to determine the re-estimation formula for
each type of HMM parameters given by
π
h+1
i
=
ϑ
π
−1 +
∑
K
k=1
γ
k
1
(i)
|S|ϑ
π
−|S|+ K
a
h+1
i j
=
ϑ
a
−1 +
∑
K
k=1
∑
T
k
−1
t=1
ε
k
t
(i, j)
|S|ϑ
a
−|S|+
∑
K
k=1
∑
T
k
−1
t=1
γ
k
t
(i)
µ
h+1
i
=
ε
i
η
i
+
∑
K
k=1
∑
T
k
t=1
γ
k
t
(i) ·o
k
t
ε
i
+
∑
K
k=1
∑
T
k
t=1
γ
k
t
(i)
σ
h+1
i
=
v
u
u
t
∆
i
+
∑
K
k=1
∑
T
k
t=1
γ
k
t
(i) ·(o
k
t
−µ
h+1
i
)
2
2r
i
+ 2 +
∑
K
k=1
∑
T
k
t=1
γ
k
t
(i)
with ∆
i
= ε
i
(µ
h+1
i
−η
i
)
2
+ 2α
i
. We calculate the
probabilities γ
k
t
(i) = P[q
t
= i|o
k
,λ
h
] and ε
k
t
(i, j) =
P[q
t
= i, q
t+1
= j|o
k
,λ
h
] using the Forward-Backward
algorithms for HMMs (Rabiner, 1989; Durbin et al.,
1998). Starting with the initial HMM λ
1
(h = 1), we
iteratively determine new HMM parameters λ
h+1
and
stop if the increase of the log-posterior of two succes-
sive training iterations is less than 10
−3
.
2.2.5 Segment Detection and Scoring
After the training of the initial HMM on all
Array-CGH profiles, we apply the Viterbi algorithm
(Rabiner, 1989; Durbin et al., 1998) to determine the
most probable state sequence q for each Array-CGH
profile o. The so-called Viterbi path q partitions
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
6
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
1 2 3 4 5
−7
−5
−3
−1
Segment Length
Mean Log−Ratio
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
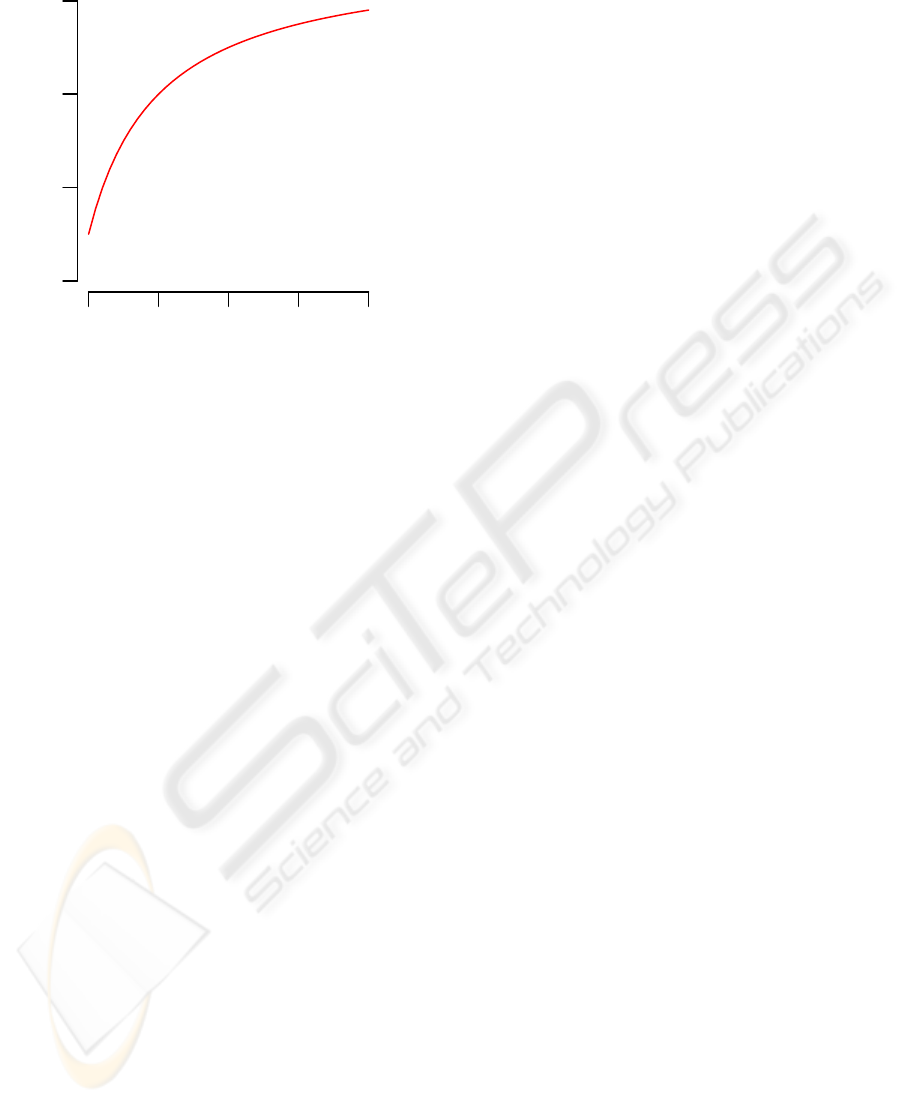
Figure 3: Visualization of the scoring scheme for DNA seg-
ments with decreased copy numbers. The red dot character-
izes a DNA segment with segment length N = 3, mean log-
ratio L = −2, and score S = N ·L = −6, which was predicted
to have a decreased copy number status by the trained HMM
in the original Array-CGH data. The red curve represents
the hyperbola f (n) = S/n of segment length n that divides
the segments with decreased copy number status obtained
from the permuted Array-CGH profiles into segments with
scores greater than −6, represented by black dots, and seg-
ments with scores less or equal than −6, represented by gray
dots. The Score-value of the segment represented by the red
dot is the proportion of gray dots in relation to the total num-
ber of gray and black dots. Here, the Score-value is 0.088.
the corresponding Array-CGH profile into DNA seg-
ments of decreased, unchanged, or increased copy
numbers in relation to the reference genome se-
quence. We refer to such a segment of copy number
status i ∈ S by
q
t
e
t
s
(i) = q
t
s
,...,q
t
e
where the length of this segment is maximal (q
t
s
−1
6=
i and q
t
e
+1
6= i for t
s
≤ t
e
), and all tiles within this
segment have the identical copy number status i (q
t
=
i for each t ∈ [t
s
,t
e
]). We score each segment by the
sum of its log-ratios
S(q
t
e
t
s
(i)|o) = N
t
e
t
s
·L
t
e
t
s
=
t
e
∑
t=t
s
o
t
to incorporate the segment length N
t
e
t
s
= t
e
−
t
s
+ 1 with respect to the mean log-ratio L
t
e
t
s
=
(1/N
t
e
t
s
)
∑
t
e
t=t
s
o
t
within the segment. Next, we deter-
mine the relevance of predicted DNA segments with
decreased or increased copy numbers. That is, we per-
mute the log-ratios of each Array-CGH profile, and
then, we apply the trained HMM to this data to pre-
dict DNA segments with changed copy numbers that
we score by S(q
t
e
t
s
(i)|o). We repeat this step 100 times
resulting in two score distributions: one for DNA seg-
ments with decreased copy numbers and another one
for DNA segments with increased copy numbers. The
Score-value of a predicted segment in the original data
is calculated by determining the proportion of scores
under the corresponding score distribution that are
identical or more extreme than the score of the con-
sidered segment. DNA segments with a Score-value
close to zero are of most interest for our biologists.
Fig. 3 shows an illustration of the scoring scheme.
3 RESULTS AND DISCUSSION
With the aim of predicting DNA copy number vari-
ations between Arabidopsis thaliana ecotype C24
and Columbia, we separately trained one HMM for
each of the two arrays of the Array-CGH experi-
ment. Then, we used each trained HMM to de-
termine DNA segments with decreased or increased
copy numbers that we scored under permuted data
for obtaining segments of decreased or increased copy
numbers at a Score-value level of 0.01. Alternatively,
the standard service of Roche NimbleGen, Inc. in-
cluded the segmentation of Array-CGH profiles us-
ing their segMNT algorithm (Roche NimbleGen, Inc.,
2008) resulting in two genome-wide segmentation
profiles. The first goal of the following study is to
investigate where the predictions of the HMM ap-
proach overlap and where they differ from those of
the segMNT algorithm. The second goal is to char-
acterize the prediction behavior of both methods for
various levels of log-ratio signal intensities.
3.1 Comparison of Segmentations
Based on the SignalMap viewer (Roche NimbleGen,
Inc.), we performed a genome-wide inspection of the
segmentation results obtained by the HMM approach
and by the segMNT algorithm. In practice, this basic
step allows a first direct comparison of both methods,
and it provides a general overview of DNA regions
where copy number variations have occurred. Both
approaches predicted DNA segments with decreased
or increased copy numbers widely spread over the
reference genome of Arabidopsis thaliana ecotype
Columbia. For the HMM approach we could quan-
tify the proportion of these segments directly, because
each of these segments is assigned to one of the three
HMM states modeling the underlying copy number
(Fig. 2). Considering the segMNT algorithm, this
ARRAY-BASED GENOME COMPARISON OF ARABIDOPSIS ECOTYPES USING HIDDEN MARKOV MODELS
7

●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Log−Ratio
−6
−4
−2
0
2
4
Log−Ratio
HMM C24 vs. Col
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Log−Ratio
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
−6
−4
−2
0
2
4
Chromosomal Location
Log−Ratio
segMNT C24 vs. Col
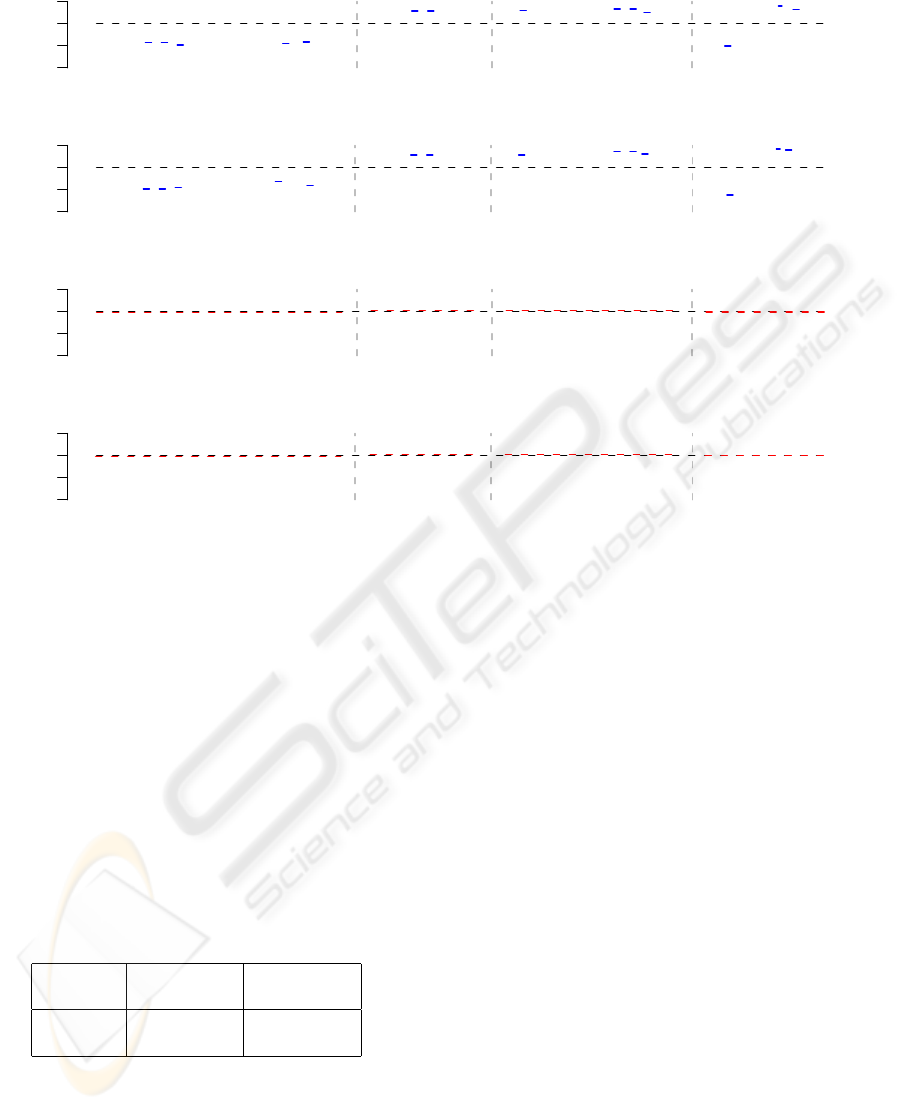
Figure 4: Exemplary comparison of segmentation results for genome-wide selected DNA regions for ecotype C24 compared
to Columbia. From left to right separated by gray dashed lines: Region 1 [Chr1 2,779,800 bp - 2,806,847 bp], Region 2
[Chr2 2,067,828 bp - 2,109,088 bp], Region 3 [Chr4 11,026,348 bp - 11,125,315 bp], and Region 4 [Chr4 13,596,032 bp -
13,665,842 bp]. The top plot represents the segmentation results of the HMM approach. Green dots label tiles predicted by the
HMM to have a decreased copy number. Red dots label tiles predicted by the HMM to have an increased copy number. Blue
dashed lines highlight DNA segments significantly different from permuted data at a Score-value threshold of 0.01. Black
dots label tiles predicted by the HMM to have unchanged copy numbers. The bottom plot represents the segmentation results
of the segMNT algorithm colored like the HMM segmentation. Both approaches provide a nearly identical segmentation of
the displayed DNA regions.
was not directly possible, because the obtained seg-
ments are not grouped by copy number status. That
is, the segMNT algorithm is only performing a seg-
mentation of the Array-CGH profiles, but the pre-
dicted segments are not categorized into segments
with decreased, unchanged, and increased copy num-
bers. Thus, we categorized all segments predicted
by the segMNT algorithm with a mean log-ratio less
or equal than −0.5 as segments with decreased copy
numbers, and in analogy, we labeled all segments
with mean log-ratios greater or equal than 0.5 as
segments with increased copy numbers. For a first
comparison of segments that have been predicted by
both methods, we only count a segment predicted by
the HMM at a Score-value level of 0.01 as a seg-
ment with decreased copy number if its correspond-
ing mean log-ratio is less or equal than −0.5, and oth-
erwise as a segment with increased copy number if
its mean log-ratio is greater or equal than 0.5. The
numbers of predicted segments for each approach are
shown in Tab. 1. DNA segments which are deleted
in Columbia, but which exist in C24 cannot be mea-
sured, because the tiling arrays represent the reference
genome of ecotype Columbia. Thus, it is expected
that the small proportion of DNA segments with in-
creased copy numbers is caused by this kind of ar-
ray design (Fig. 1). The HMM approach identified
significantly more DNA segments with decreased or
increased copy numbers than the segMNT algorithm.
These numbers alone cannot be used to decide which
method should be preferred for the comparison of
Arabidopsis thaliana ecotypes as also the lengths
Table 1: Number of segments with decreased (−) and in-
creased (+) copy numbers in ecotype C24 predicted by
HMM and segMNT.
Array 1 Array 2
Method − + − +
HMM 1352 196 1427 205
segMNT 271 3 247 4
of predicted segments, their chromosomal locations,
and their reproducibility between both arrays should
be considered. To address this, we first analyzed
the overlap of segments predicted for both arrays by
HMM or segMNT. The results are shown in Tab. 2. In
general, both methods showed a good reproducibil-
ity of their predicted segments. The higher num-
ber of predicted segments by the HMM (Tab. 1) did
not lead to a great loss of reproducibility. That is,
the HMM predicted more reproducible segments for
both arrays than the segMNT algorithm. Next, we in-
vestigated how many of the segments that were pre-
dicted by the segMNT algorithm have also been iden-
tified by the HMM. All segMNT segments of Tab. 1
were also predicted by the HMM with respect to
slightly varying segment start and end points. The
general overlap between both approaches is exemplar-
ily shown for selected DNA segments in Fig. 4. Ad-
ditionally, Fig. 5 shows representative DNA regions
where the HMM identified a copy number change
reproducible for both interleaved arrays whereas the
segMNT algorithm failed.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
8
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Log−Ratio
−4
−2
0
2
Log−Ratio
HMM C24 vs. Col Array 1
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Log−Ratio
−4
−2
0
2
Log−Ratio
HMM C24 vs. Col Array 2
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Log−Ratio
−4
−2
0
2
Log−Ratio
segMNT C24 vs. Col Array 1
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
Log−Ratio
−4
−2
0
2
Chromosomal Location
Log−Ratio
segMNT C24 vs. Col Array 2
Figure 5: Exemplary comparison of segmentation results for DNA regions on chromosome 4 for ecotype C24 compared to
Columbia. From left to right separated by gray dashed lines: Region 1 [654,108 bp - 697,518 bp], Region 2 [1,305,320
bp - 1,324,132 bp], Region 3 [3,731,013 bp - 3,761,229 bp], and Region 4 [5,411,025 bp - 5,433,126 bp]. The two top plots
represent segmentation results of the HMM approach for both interleaved arrays. Green dots label tiles predicted by the HMM
to have a decreased copy number. Red dots label tiles predicted by the HMM to have an increased copy number. Blue dashed
lines highlight DNA segments significantly different from permuted data at a Score-value threshold of 0.01. Black dots label
tiles predicted by the HMM to have unchanged copy numbers. The two bottom plots represent segmentation results of the
segMNT algorithm for both arrays. Red dashed lines show that no segmentation was obtained. Both approaches provide a
quite different segmentation of the DNA regions. Here, the segMNT algorithm failed to identify segments with decreased
or increased copy numbers. The HMM approach clearly identifies segments with significantly decreased or increased copy
numbers, and in addition, these biologically interesting results are reproducible for both arrays.
Table 2: Number of reproducible segments between Array 1
and Array 2 for HMM and segMNT based on predicted seg-
ments of Tab. 1. Ai vs. A j: Segments predicted for Array
i that are also predicted for Array j. Differences in counts
result mostly from segments predicted in one array that are
predicted in the other array by several non-overlapping seg-
ments.
A1 vs. A2 A2 vs. A1
Method − + − +
HMM 1114 119 1209 129
segMNT 232 3 224 3
3.2 Genome-wide Performance
The true copy number status of a predicted segment
can be experimentally validated using independent
methods like PCR, sequencing, or insitu hybridiza-
tion in the wet-lab. For thousands of identified seg-
ments with putative copy number variations the usage
of such validation methods is currently not practical.
In order to investigate how the prediction results of
the segMNT algorithm and the HMM approach dif-
fered at various log-ratio levels, we used a biolog-
ically motivated model that defined the copy num-
ber status of each tile with respect to its measured
log-ratio. Based on the measurements of Array-CGH
experiments, segments with decreased copy numbers
consist of tiles with log-ratios much less than zero,
and segments with increased copy number are repre-
sented by tiles with log-ratios much greater than zero
(Fig. 1). For these reasons, we use a variable log-ratio
threshold ∆ ∈ R
+
to define the copy number status
for each tile in an Array-CGH profile. That is, a tile
with log-ratio o
t
is defined to have a decreased copy
number if its log-ratio o
t
is less or equal to the log-
ratio threshold −∆, or conversely this tile is defined
ARRAY-BASED GENOME COMPARISON OF ARABIDOPSIS ECOTYPES USING HIDDEN MARKOV MODELS
9
HMM HMM
segMNT segMNT
0 0.02 0.04 0.06
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
0.0
0.2
0.4
0.6
0.8
1.0
FPR
TPR
∆∆
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
0.00 0.01 0.02 0.03 0.04 0.05
0.0
0.2
0.4
0.6
0.8
1.0
FPR
TPR
●
●
●
●
●
●
●
●
Figure 6: Prediction results obtained by segMNT and HMM at various log-ratio levels ∆ ∈ [0.5,4]. Left: FPR vs. TPR in the
context of the variable log-ratio threshold ∆ defining the copy number of segments as being decreased or increased. Right:
Top view on the left figure neglecting the log-ratio threshold.
to have an increased copy number if its log-ratio o
t
is
greater or equal to the log-ratio threshold ∆. All tiles
that are not defined to have decreased or increased
copy numbers are defined to have an unchanged copy
number. Based on that, we evaluated both segmen-
tations, the one of the HMM at a Score-value level of
0.01 and the other one of the segMNT algorithm from
the previous section, against the segmentations ob-
tained from systematically chosen variable log-ratio
thresholds ∆ ∈ [0.5,4.0]. For each log-ratio thresh-
old ∆ we determined the True-Positive-Rate TPR =
TP/(TP + FP) and the FPR = FP/(FP + TN) of both
approaches. The results are shown in Fig. 6. In gen-
eral, the HMM showed a much higher TPR than the
segMNT algorithm at a moderately higher FPR. This
confirms the previous findings: the HMM approach
identifies much more DNA segments with copy num-
ber variations.
4 CONCLUSIONS
We introduced a three-state HMM approach (Fig. 2)
for comparing the genomes of different ecotypes of
Arabidopsis thaliana. This approach is capable of
(i) incorporating biologically a priori knowledge into
the training of model parameters, and of (ii) scoring
DNA segments of decreased or increased copy num-
bers separately using permuted Array-CGH data. We
observed that our HMM approach identifies signif-
icantly more reproducible DNA segments with de-
creased or increased copy numbers than the rou-
tinely used segMNT algorithm. Using this HMM ap-
proach, we find that about 5% of the genome of eco-
type C24 shows decreased copy numbers and 0.3%
shows increased copy numbers compared to the ref-
erence genome of ecotype Columbia. Thus, we ob-
tained a detailed map characterizing regions of DNA
copy number variations for future studies of eco-
types including the analysis of DNA-histone interac-
tions, histone modifications, and transcript profiling.
Further biological interpretation of such a map can
be obtained using the AtEnsEMBL genome browser
(James et al., 2007) for representing the map in the
context of the genome annotation. In summary, all
results indicate that our HMM approach provides a
good basis for Array-CGH-based genome comparison
of Arabidopsis thaliana ecotypes. One of our future
analyses will focus on an in-depth comparison of the
HMM approach against other available methods for
analyzing Array-CGH data.
ACKNOWLEDGEMENTS
This work was supported by the Ministry of culture
Saxony-Anhalt grant XP3624HP/0606T and by the
DFG grant HO1779/7-2.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
10

REFERENCES
Baum, L. E. (1972). An equality and associated maximiza-
tion technique in statistical estimation for probabilistic
functions of Markov processes. Inequalities, 3:1–8.
Borevitz, J. O., Liang, D., Plouffe, D., Chang, H.-S., Zhu,
T., Weigel, D., Berry, C. C., Winzeler, E., and Chory,
J. (2003). Large-scale identification of single-feature
polymorphisms in complex genomes. Genome Res,
13:513–523.
Cahan, P., Godfrey, L. E., Eis, P. S., Richmond, T. A.,
Selzer, R. R., Brent, M., McLeod, H. L., Ley, T. J.,
and Graubert, T. A. (2008). wuHMM: a robust al-
gorithm to detect DNA copy number variation using
long oligonucleotide microarray data. Nucleic Acids
Research, 36(7):1–11.
Dempster, A., Laird, N., and Rubin, D. (1977). Maxi-
mum likelihood from incomplete data via the EM al-
gorithm. Journal of the Royal Statistical Society, Se-
ries B, 39(1):1–38.
Durbin, R., Eddy, S., Krogh, A., and Mitchision, G. (1998).
Biological sequence analysis - Probabilistic models
of proteins and nucleic acids. Cambridge University
Press.
Fan, C., Vibranovski, M. D., Chen, Y., and Long, M. (2007).
A Microarray Based Genomic Hybridization Method
for Identification of New Genes in Plants: Case Anal-
yses of Arabidopsis and Oryza. J Integr Plant Biol,
49(6):915–926.
Fridlyand, J., Snijders, A. M., Pinkel, D., Albertson, D. G.,
and Jain, A. N. (2004). Hidden Markov models ap-
proach to the analysis of array CGH data. J Multivari-
ate Analysis, 90:132–153.
Hup
´
e, P., Stransky, N., Thiery, J.-P., Radvanyi, F., and Bar-
illot, E. (2004). Analysis of array CGH data: from
signal ratio to gain and loss of DNA regions. Bioin-
formatics, 20(18):3413–3422.
James, N., Graham, N., Celments, D., Schildknecht, B., and
May, S. (2007). AtEnsEMBL: A Post-Genomic Re-
source Browser for Arabidopsis. Methods Mol Biol,
406:213–228.
Jong, K., Marchiori, E., Meijer, G., Vaar, A. v. d., and Yl-
stra, B. (2004). Breakpoint identification and smooth-
ing of array comparative genomic hybridization data.
Bioinformatics, 20(18):3636–3637.
Lai, W. R., Johnson, M. D., Kucherlapati, R., and Park, P. J.
(2005). Comparative analysis of algorithms for identi-
fying amplifications and deletions in array CGH data.
Bioinformatics, 21(19):3763–3770.
Mantripragada, K. K., Buckley, P. G., de Stahl, T. D., and
Dumanski, J. P. (2004). Genomic microarrays in the
spotlight. Trends Genet, 20:87–94.
Marioni, J. C., Thorne, N. P., and Tavar
´
e (2006). BioHMM:
a heterogeneous hidden Markov model for segmenting
array CGH data. Bioinformatics, 22(9):1144–1146.
Martienessen, R. A., Doerge, R. W., and Colot, V. (2005).
Epigenomic mapping in Arabidopsis using tiling mi-
croarrays. Chromosome Research, 13:299–308.
Rabiner, L. (1989). A Tutorial on Hidden Markov Mod-
els and Selected Applications in Speech Recognition.
Proceedings of the IEEE, 77(2):257–286.
Richardson, S. and Green, P. J. (1997). On Bayesian Analy-
sis of Mixtures with an Unknown Number of Compo-
nents. Journal of the Royal Statistical Society, Series
B, 59(4):731–792.
Roche NimbleGen, Inc. (2008). A Performance Com-
parison of Two CGH Segmentation Analysis Algo-
rithms: DNACopy and segMNT. Available online:
http://www.nimblegen.com.
Rueda, O. M. and D
´
ıaz-Uriate, R. (2007). Flexible and
Accurate Dection of Genomic Copy-Number Changes
from aCGH. PLoS Comput Biol, 3(6).
Willenbrock, H. and Fridlyand, J. (2005). A comparison
study: applying segmentation to array CGH data for
downstream analyses. Bioinformatics, 21(22):4084–
4091.
ARRAY-BASED GENOME COMPARISON OF ARABIDOPSIS ECOTYPES USING HIDDEN MARKOV MODELS
11
