
Pearling: Stroke Segmentation with Crusted Pearl
Strings
B. Whited
1
, J. Rossignac
1
, G. Slabaugh
2
, T. Fang
2
and G. Unal
2
1
Georgia Institute of Technology, Graphics, Visualization and Usability Center
Atlanta, GA 30332, USA
2
Siemens Corporate Research, Intelligent Vision and Reasoning Department
Princeton, NJ 08540, USA
Abstract. We introduce a novel segmentation technique, called Pearling, for the
semi-automatic extraction of idealized models of networks of strokes (variable
width curves) in images. These networks may for example represent roads in an
aerial photograph, vessels in a medical scan, or strokes in a drawing. The operator
seeds the process by selecting representative areas of good (stroke interior) and
bad colors. Then, the operator may either provide a rough trace through a particu-
lar path in the stroke graph or simply pick a starting point (seed) on a stroke and a
direction of growth. Pearling computes in realtime the centerlines of the strokes,
the bifurcations, and the thickness function along each stroke, hence producing a
purified medial axis transform of a desired portion of the stroke graph. No prior
segmentation or thresholding is required. Simple gestures may be used to trim
or extend the selection or to add branches. The realtime performance and relia-
bility of Pearling results from a novel disk-sampling approach, which traces the
strokes by optimizing the positions and radii of a discrete series of disks (pearls)
along the stroke. A continuous model is defined through subdivision. By design,
the idealized pearl string model is slightly wider than necessary to ensure that it
contains the stroke boundary. A narrower core model that fits inside the stroke
is computed simultaneously. The difference between the pearl string and its core
contains the boundary of the stroke and may be used to capture, compress, visu-
alize, or analyze the raw image data along the stroke boundary.
1 Introduction
In this paper, we present Pearling, for the extraction and modeling of stroke-like struc-
tures in images. This work is motivated by the need for semi-automatic segmentation
tools, particularly in the analysis of medical images. Indeed, every year millions of
medical images are taken, many of which are used to support clinical applications in-
volving diagnosis (e.g., stenosis, aneurysm, etc.) surgical planning, anatomic modeling
and simulation, and treatment verification. These applications either benefit from, or are
required to have, a geometric model of the important structures (blood vessel, airway,
etc.) being studied. Segmentation of stroke-like structures such as blood vessels is a fun-
damental problem in medical image processing, and arises in other contexts including
industrial applications as well as aerial/satellite image analysis.
Whited B., Rossignac J., Slabaugh G., Fang T. and Unal G. (2008).
Pearling: Stroke Segmentation with Crusted Pearl Strings.
In Image Mining Theory and Applications, pages 103-112
DOI: 10.5220/0002340801030112
Copyright
c
SciTePress

With manual segmentation techniques, it is possible to obtain highly accurate re-
sults. However, these methods typically require an excessive amount of tedious labor to
be practical in a clinical workflow. While fully automatic segmentation methods can be
desirable in these applications, given the poor contrast, noise, and clutter that is com-
mon to medical images, it is often difficult for fully automatic segmentation methods
to yield robust results. Furthermore, often one is interested in extracting only a sub-
set, for example a specific path through a branching network of stroke-like structures.
Therefore, there is a salient need for interactive segmentation methods that are mostly
automatic, but do accept input from the operator to guide the segmentation in a particu-
lar direction, quickly correct for errant segmentations, and add branches to an existing
segmentation result. Crucial to such a semi-automatic segmentation method is computa-
tional efficiency, so that the operator will not have to wait for segmentation results while
interacting with the data. Furthermore, to support further analysis or close-up visualiza-
tion it may be important to identify the portion of the image (crust) that surrounds the
stroke boundary.
1.1 Related Work
Given its clinical importance, the problem of vessel segmentation has received a fair
amount of attention in the literature. Kirbas et al. [1] present a recent survey that pro-
vide a recent survey of techniques for vessel segmentation. They conclude that there is
no single vessel segmentation approach that is robust, automatic, and fast, and that suc-
cessfully extracts the vasculature across all imaging modalities and different anatomic
regions. Following their conclusion, we step away from total automation and instead fo-
cus in interactive segmentation, providing an efficient system for an operator to quickly
extract the region and branches of interest.
Other recent vessel segmentation approaches in the medical imaging literature in-
clude [2], who model vessel segments using superellipsoids, [3], who implement co-
dimension two level set flows, and [4], who apply a Bayesian classifier to feature vec-
tors produced using Gabor wavelets. While elegant, these techniques require significant
computational resources. Fast methods such as [5] perform the segmentation on slices
made in a direction orthogonal to the vessel centerline or intensity maxima [6] and
then extract the vessel geometry by connecting the results. More closely related to our
work is [7], who build tunnels modeled as a union of spheres, placed through protein
molecules using a Voronoi diagram pre-computed on a segmented version of the image.
Unlike this work, our method is image-based and designed for segmentation, placing
the pearls using local pixel intensity inside each pearl.
Several authors proposed to compute skeletons through the advection of mass along
the distance field [8] [9]. The thinning methods [10] and the methods based on distance
transform [11] for extracting a skeleton are not easily applicable to our problem of
rapidly segmenting a subset of the volume because they are global and hence slow
and require the precomputation of a distance field. The distance field pre-computation
may be avoided in methods that use a general scalar field [12]. Minimal paths through
vessels have been computed using fast marching techniques [13] that backtrack along a
distance field [14] computed with a Riemannian metric.
104104

Also related is the computation of the medial axis transform [15]. Once an image is
segmented and pixels have been identified that are in the stroke network, techniques for
selecting the center line and medial axis could be used. Pearling produces directly the
purified result that could be derived by removing automatically small branches from
the MAT and selecting a desired portion of the graph, all without requiring a prior
segmentation.
The application of this technique to tracing 3D networks of vessels has been dis-
cussed [16], but is not the same paradigm as input is more tedious and requires a differ-
ent user interaction.
1.2 Our Contribution
Pearling is a novel method for segmentation of stroke networks in images. Pearling per-
forms a segmentation and idealization simultaneously by computing an ordered series
of pearls, which are disks of possibly different radii. Starting with an initial pearl given
by the operator, as well as an initial direction, pearling iteratively computes the position
and radius of an adjacent pearl based on the image data, so that the newly placed pearl
fits properly along the stroke, slightly building bulging out on both sides. The method
proceeds in this fashion, producing a string or network of strings of pearls that pro-
vide a discrete representation of the stroke geometry. Pearling is robust to fluctuations
in image intensities (due to noise, etc.) as the forces acting on a pearl are integrated
over the region inside the pearl. A final smooth contour representing the stroke net-
work is then obtained by estimating continuous functions that interpolate the discrete
series of pearls. As we will show, pearling is computationally efficient and well suited
to user interactivity. This interactivity affords operator guidance of the segmentation in
a particular direction as well as operator correction of errant segmentation results.
In addition to pearls, we introduce the concepts of core and crust. The core of the
pearling model is computed by reducing the radius of each pearl while keeping its
center in place. The radius is chosen to be as large as possible, while ensuring that
a given majority of pixels inside the core pearl are good. The difference between the
“outer” pearl model and its core is the crust, which may be used to capture, compress,
archive, transmit, visualize, or analyze the original data along the stroke border. We
show in Section 3 that the crust is a narrow band around the stroke border computed
through region growing techniques.
2 Methodology
Pearling allows the operator to extract a higher level idealized parametric representation
of each stroke. This representation is called a string. As shown in Figure 1, it comprises
an ordered series of pearls (or disks), each defined by the location c
i
of its center, by its
radius r
i
, and a time value t
i
, and possibly other attributes a
i
. The continuous model of
the corresponding stroke that is recovered by Pearling is defined as the region W swept
by a pearl whose center c(t) and radius r(t) are both continuous and smooth functions
of the time parameter t. These functions interpolate the centers and radii of the string
of pearls for given values t
i
of time. For a network of strokes, multiple strings will be
defined which meet at bifurcation pearls, which will be defined later.
105105
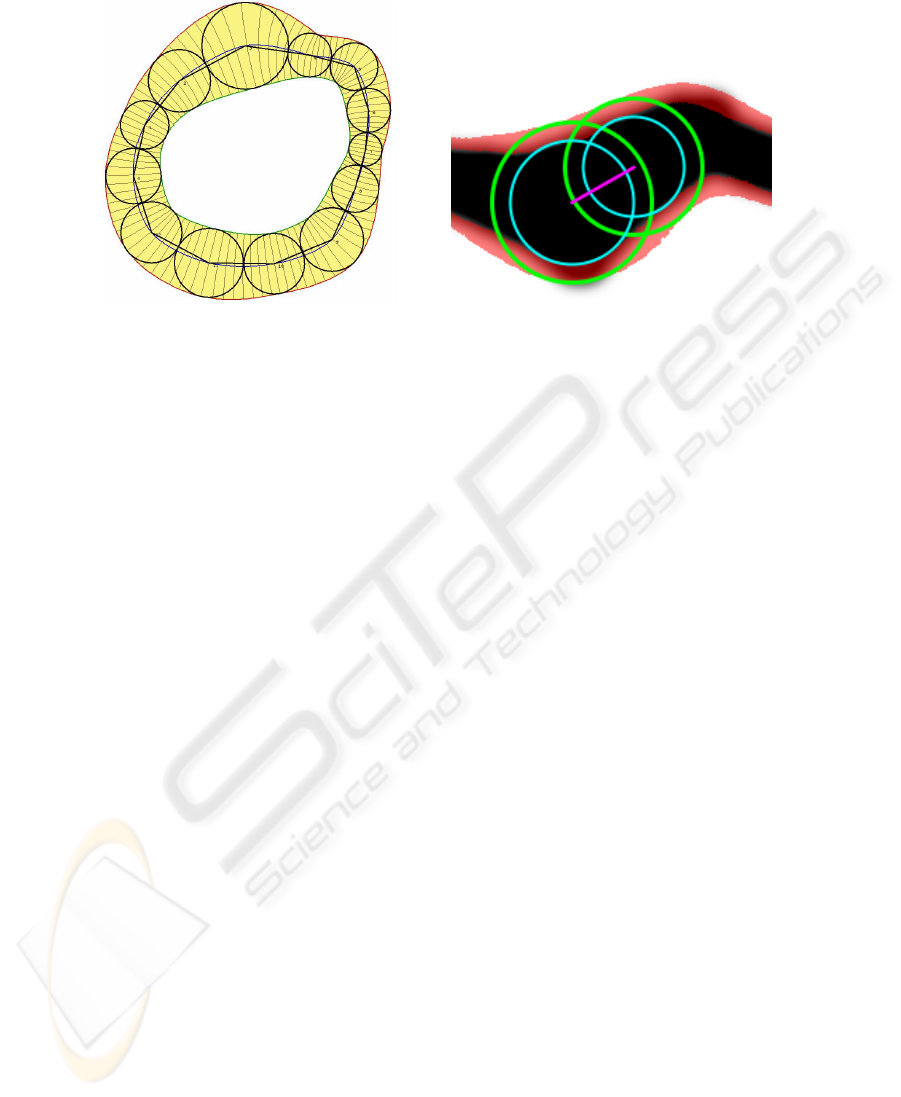
Fig. 1. Representation of Pearling, which con-
sists of an ordered series of pearls. Continu-
ous functions that interpolate the pearls are
also shown: the blue curve interpolates the
pearl centers, and the red and green curves in-
terpolate the outside and inside edges of the
pearls, respectively.
Fig. 2. Two adjacent Pearls (green) and their
cores (cyan) with their centers connected
(magenta) overlaid on top a stroke (black) and
the crust region defined by the continuous set
of pearls minus their cores (red).
2.1 Estimation of Pearls
Pearling starts with an initial seed, c
0
, which is a point either provided by an operator or
by an algorithm. Typically, c
0
should be chosen to lie close to the centerline of a stroke
and possibly at the end of one of the strokes of the desired structure. Pearling then uses
an iterative process to construct an ordered series of pearls, one at a time. During that
process, at each step, the center c
i
and radius r
i
of the current pearl is chosen so as
to maximize r
i
subject to image data, given the constraint that the distance d
i
between
c
i
and the center c
i−1
of the previous pearl is bound by functions d
min
(r
i−1
, r
i
) and
d
max
(r
i−1
, r
i
). We use linear functions d
min,max
(r
i−1
, r
i
) = ar
i−1
+ br
i
, and with
bounds d
min
(r
i−1
, r
i
) = r
i
/2 and d
max
(r
i−1
, r
i
) = r
i−1
+ r
i
. It is important that
d
i
be allowed to fluctuate in order to capture rapid changes in thickness and allow
convergence to local minima.
Let c
i−1
be the center of the previous pearl seed, as shown in Figure 2. Let c
i
be
the center of the next pearl, and let r
i
be its radius. The objective is to find the optimal
values of c
i
and r
i
that place the ith pearl in the stroke. The location of c
i
may be
specified in polar coordinates around c
i−1
. In order to adjust the values of r
i
and c
i
so
that the pearl better fits snugly astride the stroke, we define two functions: f (c
i
, r
i
) and
g(c
i
, r
i
), as described below.
Center Estimation. The function f (c
i
, r
i
) returns a gradient indicating the direction
in which c
i
should be adjusted and the amount of the adjustment. This adjustment can
then be converted to an angle relative to c
i−1
and applied to o
i
. f(c
i
, r
i
) takes the form,
106106

f (c
i
, r
i
) =
15
2πr
2
i
Z
x∈P
i
φ(x)(c
i
− x)
1 −
kc
i
− xk
2
r
2
i
dx (1)
φ(x) =
1, if ˆp
out
(I(x)) > ˆp
in
(I(x))
0, otherwise
(2)
The function f (c
i
, r
i
) sums the vectors (c
i
− x), where x is the vector coordinate of the
the current pixel, across the entire area of pixels for pearl P
i
, using only those pixels
such that φ(x) = 1, i.e., pixels determined to be outside the stroke. Each of these
vectors is weighted by its distance from c
i
such that pixels nearer c
i
have a stronger
influence on the result, as reflected in the
1 −
kc
i
−xk
2
r
2
i
component of Equation 1.
Intuitively, Equation 2 states that each point inside the ith pearl but outside the stroke
imparts a force on the pearl that pushes it away from the stroke boundary. When the
forces are balanced on all sides of the pearl, the pearl is typically centered in the vessel.
The
15
2πr
2
i
is a normalization factor computed by looking at the case where a pearl is cut
into two equal halves by a linear boundary separating good and bad pixels. By assuming
this ideal case, we can compute the factor by calculating the offset needed to move this
pearl half the minimum distance that would move it entirely in the good region.
Determination of whether a pixel lies inside the stroke or outside the stroke is
necessary when computing f (c
i
, r
i
), and is achieved using non-parametric density es-
timation. Before running the algorithm, the operator selects two regions; one inside
the stroke and one outside. For a given region, we estimate the density by applying a
smoothing kernel K to the pixels in the region’s histogram, i.e.,
ˆp =
1
n
n
X
i=1
K
I
i
− m
h
, (3)
where I
i
is the intensity of the ith pixel in the region, m is the mean of intensities of
the n pixels in the region, and h is the bandwidth of the estimator. We use a Gaussian
kernel, K(u) =
1
√
2π
e
−
1
2
u
2
. Performing this estimation on two operator-supplied re-
gions results in two densities, ˆp
in
(I) and ˆp
out
(I). During segmentation, an intensity I
is classified as outside if ˆp
out
(I) > ˆp
in
(I); otherwise it is classified as inside.
Radius Estimation. r
i
is adjusted to better fit the stroke using the function g(c
i
, r
i
),
as shown in Equation 4. For robustness, pearls are designed to have a percentage p of
their pixels inside the tube and the rest outside the tube, as indicated in Figure 2. In our
implementation, g(c
i
, r
i
) is positive when less than p percent of the pearl’s pixels fit in
the tube and negative more than 1 − p of the pixels lie outside of the tube. The portion
of the enlarged pearl that lies outside of the tube is typically computed by sampling the
pearl’s interior, however, alternatively one can sample the pearl’s boundary. The result
of g(c
i
, r
i
) is then used to scale r
i
to better fit in the tube. g(c
i
, r
i
) takes the form,
g(c
i
, r
i
) = p −
R
x∈P
i
(1 − φ(x)) dx
R
x∈P
i
dx
(4)
107107

Interleaving the Estimation and Convergence. We interleave the estimation of c
i
and
r
i
for the ith pearl P
i
. For a given position c
i
and radius r
i
, one can update both param-
eters independently using the results given by f (r
i
, c
i
) and g(r
i
, c
i
). In both cases, the
quality of the fit is measured and the desired adjustment is computed and returned.
The adjustments of c
i
and r
i
are done through several iterations while enforcing
the constraint on d
i
until the adjustment values returned by f (c
i
, r
i
) and g(c
i
, r
i
) fall
below a given threshold. The process then freezes the current pearl and starts fitting the
next one. The growth of a stroke stops when the radius of the next pearl falls outside
of a prescribed range, or when another application-dependent criterion is met, such as
the detection of an operator-supplied endpoint. The result of this Pearling process is a
series of location-radius pairs (c
i
, r
i
), which we call the control pearls.
2.2 Direction Estimation and Bifurcations
Often in the applications targeted, images contain sharp turns and bifurcations where a
stroke will branch into multiple strokes and may even contain loops. We have extended
the above process to support these options.
Fig. 3. A pearl shown at a stroke bifurcation along with its set of good pixels in the region
bounded by r
i
and kr
i
. Each connected component C
j
is uniquely colored. Vectors D
j
(ma-
genta) are shown for the connected components which contain a number of pixels greater than
the set threshold.
Once a pearl P
i
has converged to fit on a stroke, an analysis of the region around P
i
is done in order to decide where to initially position P
i+1
, taking into account that
there could be more than one P
i+1
or none. This analysis is done on the pixels in a
circular band around P
i
with an outer radius kr
i
where k is some constant . For our
results, a value of k = 1.35 is used. Each pixel x in this band is then classified using
Equation 2. The result gives a classification with N > 0 connected components of
good pixels. At minimum, there should be a connected component identifying the path
from the previous pearl, P
i−1
. If N = 1, then the only possible direction is backwards
and pearling stops growing the current branch because its end has been found. If N >
1, then the starting position(s) for any subsequent pearl(s) can be chosen using the
remaining connected components. For each connected component C
j
, an average point
is calculated which defines a direction vector D
j
from the pearl center c
i
. Subsequent
pearls are then initialized to the points on the boundary points of P
i
which intersect
108108
each D
j
. This extension allows pearling to accommodate sharp turns and bifurcations
in the stroke structure.
A loop in the pearling network can also exist. A simple intersection check between
the current pearl and all previous pearls will reveal if such a loop has occurred. In this
case, the current pearl is linked to the intersected pearl and its string is ended. The
intersected pearl could then become a bifurcation pearl, if it already has more than one
adjacent pearl, or it could be the end of another stroke still in in the growing phase. If
the latter is the case, and two growing strokes collide, they are both ended and become
part of the same stroke.
2.3 Building a Continuous Model
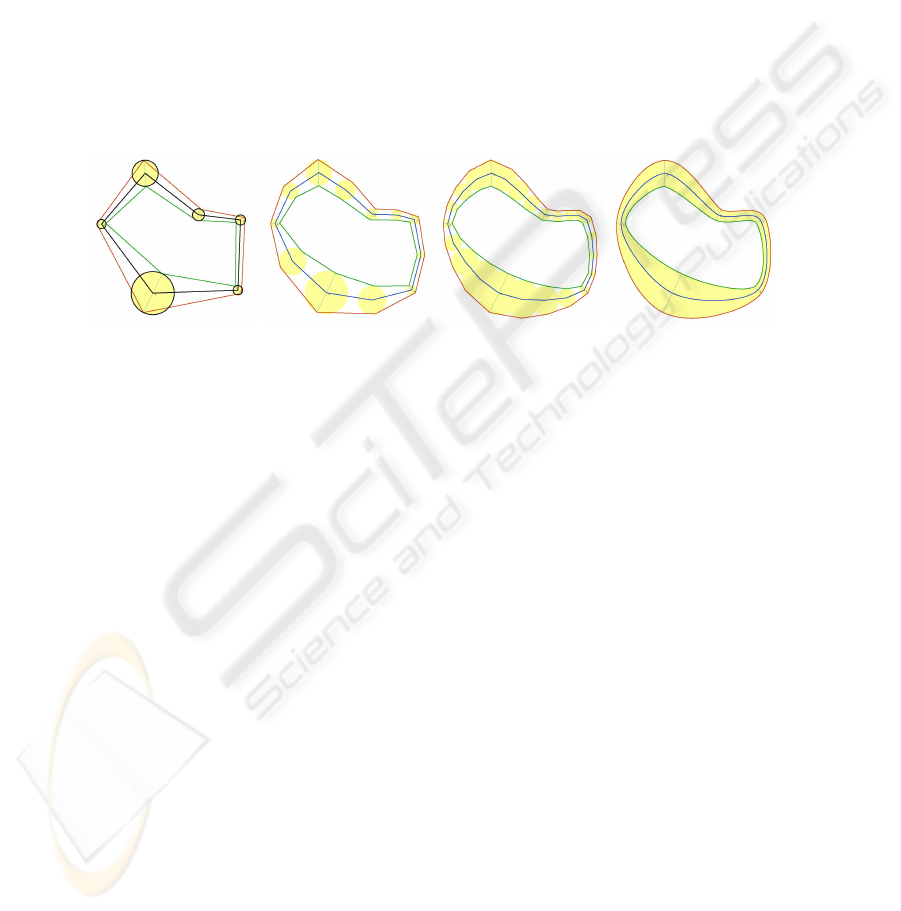
Fig. 4. Subdivision for estimating the continuous canal surface that interpolates the pearls.
A continuous model W of each stroke is obtained by computing continuous functions
c(t) and r(t) that interpolate the discrete set of end, branching and contour pearls. We
model W as the union of an infinite set of disks [17], which is and may be expressed in
parametric form as W = Disk(c(t), r(t)) for t ∈ [0, 1]. If we assume that the pearls are
more or less uniformly spaced along the stroke, we can define the string as the limit of a
four-point subdivision process, which, at each iteration, introduces a new pearl between
each pair of consecutive pearls as shown in Fig 4.
3 Results
We now present segmentation results using Pearling. We begin with the segmentation of
a satellite image of a river. The original image with the initial inputs is shown in Figure 5
(left). As described, the initial inputs include regions of good and bad pixels (shown in
green and red) and an initial point and direction (shown in orange). The algorithm then
proceeds, successively adding pearls until no more can be added, the result of which is
shown in Figure 5 (center). From the collection of discrete pearls and their cores, we
can then extract the continuous model of the crust, as seen red in Figure 5 (right). The
yellow region in the figure is the result of a simple region-growing segmentation using
the same good and bad regions and starting point as pearling. A zoomed-in section
shows almost all boundary pixels are contained within the pearling crust.
109109

Fig. 5. An unedited grayscale image obtained from satellite imagery of a river shown with the
initial inputs(left), the resulting pearling segmentation, computed in 33ms(center), and the crust
(red) overlaid atop a simple region-grown segmentation (yellow), showing that the majority of
boundary details are contained within the crust.
Fig. 6. An MR angiographic image with centerlines(left) and discrete pearls (right) computed by
pearling in 27ms on an image with size 436x168.
Fig. 7. A Chinese character with centerlines(left) and discrete pearls (right) computed by pearling
in 37ms on an image with size 236x201.
Figures 6 and 7, present more segmentation results, of an MR angiographic image, and
a variable width Chinese character. For each figure, we show the original image with the
pearling-computed centerlines (left) and the pearl disks (right). Note that all examples
completed in tens of milliseconds.
3.1 User Interactivity
As Pearling is computationally efficient, it affords the user interaction with data without
delays. In Figure 8 (left) we show an example where an operator can select a string by
simply moving the mouse over any pearl in the string. Once selected, the branch can
110110

Fig. 8. An initial incomplete pearling, with one string selected (yellow) by the operator (left). The
result of the deleting the selected string and also the initial input for a new string (orange) by the
operator (center), and the result (right).
then be deleted with the press of a key, as shown in Figure 8 (center). The operator can
also add strings to an incomplete segmentation by simply selecting a pearl and drawing
a new direction vector from it, as shown in orange in Figure 8 (center). The result of the
new string being grown is shown in Figure 8 (right).
For more control, the operator may provide a rough trace of the centerline of a
desired stroke. As the operator is manually tracing, pearls are placed at samples along
the curve and converge in real-time thus forming the stroke as the operator is tracing
it with a stylus. In this mode, the operator uses a stylus to quickly trace a rough curve
through the desired stroke structure and then as desired, adds branches. A preset mode
or the stylus speed when the stylus is released indicate how far past the release point will
pearling grow the stroke structure. As the operator is still tracing the curves, pearling
computes the idealized strokes (centerline and radius) and displays them. Each new
trace either adds or removes a branch.
4 Conclusions
In this paper we presented Pearling, a new method for semi-automatic segmentation
and geometric modeling of stroke-like structures. Pearling performs a segmentation by
computing an ordered series of pearls that discretely model the stroke structure geom-
etry. Smoothing is used to define a continuous model. The computational efficiency of
Pearling affords efficient user interaction with the segmentation, allowing the opera-
tor to correct for errant segmentation results or guide the segmentation in a particular
direction through the data.
Sometimes the idealized pearling result doesn’t contain enough information to per-
form a more precise analysis, so we presented the concept of a crust around the border
region. Important image information, such as the inner wall of an artery, is identified in
the crust region and can be used to support a more detailed analysis.
While more comprehensive validation of the algorithm is required, from our ex-
perimental results we conclude that Pearling results in highly efficient segmentation of
strokes, and holds much promise for semi-automatic image segmentation.
111111

References
1. C. Kirbas, F. Quek, A Review of Vessel Extraction Techniques and Algorithms, ACM Com-
puting Surveys 36 (2) (2004) 81–121.
2. J. A. Tyrrell, E. di Tomaso, D. Fuja, R. Tong, K. Kozak, R. Jain, B. Roysam, Robust 3-D
Modeling of Vasculature Imagery Using Superellipsoids, IEEE Trans. on Medical Imaging
26 (2) (2007) 223–237.
3. L. M. Lorigo, O. D. Faugeras, W. E. L. Grimson, R. Keriven, R. Kikinis, A. Nabavi, C.-
F. Westin, CURVES: Curve Evolution for Vessel Segmentation, Medical Image Analysis 5
(2001) 195–206.
4. J. Soares, J. Leandro, R. Cesar, H. Jelinek, M. Cree, Retinal Vessel Segmentation Using the
2-D Gabor Wavelet and Supervised Classification, IEEE Trans. on Med. Img. 25 (9) (2006)
1214–1222.
5. O. Wink, W. Niessen, M. A. Viergever, Fast delineation and visualization of vessels in 3-d
angiographic images, IEEE Trans. on Medical Imaging 19 (4) (2000) 337–346.
6. A. Szymczak, A. Tannenbaum, K. Mischaikow, Coronary vessel cores from 3D imagery:
a topological approach, in: Medical Imaging 2005: Image Processing. Proceedings of the
SPIE, Vol. 5747, 2005, pp. 505–513.
7. P. Medek, P. Benes, J. Sochor, Computation of tunnels in protein molecules using Delaunay
triangulation, in: Journal of WSCG, 2007, p. 8.
8. L. Costa, R. Cesar, Shape Analysis and Classification, CRC Press, 2001.
9. A. Telea, J. J. van Wijk, An augmented fast marching method for computing skeletons and
centerlines, in: Symposium on Data Visualisation, 2002, pp. 251–259.
10. C. Pudney, Distance-ordered homotopic thinning: A skeletonization algoritm for 3D digital
images, IEEE. Trans. on Biomedical Engineering 72 (3) (1998) 404–413.
11. M. Van Dortmont, H. van de Wetering, A. Telea, Skeletonization and distance transforms of
3d volumes using graphics hardware, in: DGCI, 2006, pp. 617–629.
12. N. Cornea, D. Silver, X. Yuan, R. Balasubramanian, Computing hierarchical curve-skeletons
of 3d objects, The Visual Computer 21 (11) (2005) 945–955.
13. H. Li, A. Yezzi, Vessels as 4D Curves: Global Minimal 4D Paths to 3D Tubular Structure
Extraction, in: Workshop on Mathematical Methods in Biomedical Image Analysis, 2006.
14. L. D. Cohen, R. Kimmel, Global minimum for active contours models: A minimal path
approach, IJCV 24 (1) (1997) 57–78.
15. H. Blum, A Transformation for Extracting New Descriptors of Shape, in: W. Wathen-Dunn
(Ed.), Models for the Perception of Speech and Visual Form, MIT Press, Cambridge, 1967,
pp. 362–380.
16. B. Whited, J. Rossignac, G. Slabaugh, T. Fang, G. Unal, Pearling: 3d interactive extraction
of tubular structures from volumetric images, in: MICCAI Workshop: Interaction in Medical
Image Analysis and Visualization, 2007.
17. G. Monge, Applications de l’analyse
`
a la g
´
eom
´
etrie, 5th Edition, Bachelier, Paris, 1894.
112112
