
AN IMPROVED STEGANOGRAPHIC METHOD
Hyoung Joong Kim and Amiruzzaman Md
Graduate School of Information Management and Security, Korea University, Anam-Dong, Seoul 136-701, Korea
Keywords:
Steganography, Steganalysis, JPEG Coefficient, Image Histogram.
Abstract:
An improved steganographic method is proposed in this paper. Two distinct methods are combined here with
optimized way with possibly high data hiding capability. The proposed method shifts the last nonzero AC
coefficients in each JPEG block, and, changes the magnitude value of the first nonzero AC coefficients.
1 INTRODUCTION
Steganography and Steganalysis are advancing at
the same time. The history of steganography and
steganalysis is a history of rat races. Whenever
a steganographic method has been proposed, the
method is about to be broken soon by new steganal-
ysis methods. Therefore, steganographers try to de-
velop new methods fully or partially secure from the
existing steganalysis methods. However, it is not pos-
sible all the time to be able to take all security issues
into account and solve in one method. It is known
that steganography is one of the oldest arts or tech-
niques for hiding data to establish a secure covert
communication channels. However, it is not so long
since the ground of digital steganography techniques
has been formed. Many innovative steganographic
algorithms are available now ((Provos 2001), (Sallee
2004), (Sallee 2005), (Solanki et al. 2007), (Westfeld
and Pfitzmann 2000)).
The most important goal of steganography is to
conceal the existence of a secret message. How-
ever, researchers are also having interest to break
steganographic schemes. There are many available at-
tacks (Fridrich, 2004) invented by several researchers.
Among them statistical attack (Westfeld 2001) is one
of the most popular and effective at-tacks in stegano-
graphic world. Another famous at-tack is the cali-
brated statistics attack (Fridrich et al. 2002), (Fridrich
et al. 2003). Data hiding methods have to be designed
to make them secure from statistical attack because
this attack is relatively easy to combat. Simple solu-
tion against this attack is keeping the same or similar
histogram to the original histogram. However, keep-
ing the same shape of a magnitude histogram is not
easy to achieve as long as the coefficient magnitudes
are modified. Note that one branch of steganography
methods is inventing schemes to preserve the origi-
nal histogram perfectly. Least significant bit over-
writing methods including OutGuess (Provos 2001)
can preserve the original histogram almost perfect,
but not absolutely perfect. This method modifies half
of the nonzero coefficients and corrects the distorted
histogram by adjusting with the rest of unused coeffi-
cients. In general, perfect preservation is not possible
because data pattern is not ideal.
F5 (Westfeld 2001) also try to narrow the gap
be-tween original and modified histograms by decre-
menting nonzero JPEG coefficients towards 0 and ap-
plying matrix embedding and permutative straddling.
Sallee models the marginal distribution of DCT coef-
ficients in JPEG-compressed images by the general-
ized Cauchy distribution (Sallee 2004). Thus, the em-
bedded message is adapted to the generalized Cauchy
distribution using arithmetic coding. Arithmetic cod-
ing transforms unevenly distributed bit streams into
shorter, uniform ones. This procedure is known as
MB1. One weak point of the MB1 is that block arti-
fact increases with growing size of the payload. MB2
has presented a method to overcome this weakness
(Sallee 2005). The MB2 embeds message in the same
way as MB1 does, but its embedding capacity is only
half of that of MB1. The other half of the nonzero
DCT coefficients is reserved for de-blocking purpose.
Preserving the perfect shape of histogram of stego
image is a primary target in the field of steganogra-
phy. For the first time one method (Amiruzzaman and
Kim, 2008) claims that their method can preserve ex-
actly the same shape of histogram in the stego image.
The main drawback of their method is low embed-
ding capacity. In this paper, a combined approach is
introduced to overcome the limitation of embedding
capacity and manage the secret data size.
The rest of this paper is organized as follows:
145
Joong Kim H. and Md A. (2008).
AN IMPROVED STEGANOGRAPHIC METHOD.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 145-150
DOI: 10.5220/0001938901450150
Copyright
c
SciTePress

In Section 2, coefficient magnitude and position his-
tograms are defined. Data hiding method based on
the position histogram is presented. Section 3 sum-
marizes experimental results. Section 4 concludes the
paper.
2 OUR APPROACH
As the proposed method works with a combination of
two different approaches, this method has to be dis-
cussed one by one: each method to hide data into ei-
ther non-sensitive or sensitive JPEG blocks. The sen-
sitive and non-sensitive blocks are separated on the
basis of the number of nonzero AC coefficients. To
select the sensitive and non-sensitive blocks, a thresh-
old value is used. Before further discussion, it is
necessary to define sensitive and non-sensitive JPEG
blocks.
2.1 Sensitive and Non-sensitive JPEG
Blocks
An image can be divided into 8×8 non-overlapping
blocks and processed in the frequency domain block
by block, where the leftmost and topmost value is a
DC coefficient value, and the other 63 coefficients
are AC coefficient values. The DC coefficient plays
an important role: it maintains an average luminance
value of the block. Hence, the DC coefficient is not
used for embedding data due to serious possibility
of blocking effects between neighboring blocks. The
sensitive and non-sensitive blocks are determined by
the number of nonzero AC coefficients. The leftmost
and topmost AC coefficients close to the DC coeffi-
cient are considered to be more important than the
rightmost and bottommost AC coefficients far from
the DC coefficient. Importance of the coefficients
can be measured by the magnitudes of the associated
quantization coefficients. In addition, in general, it
is believed that low-frequency components are more
important than high-frequency components. The pro-
posed method uses a threshold value to determine sen-
sitive and non-sensitive JPEG blocks. If a JPEG block
has less or equal to T
v
number of nonzero AC coeffi-
cients, then that block is treated as a sensitive block.
Similarly, if the numbers of nonzero AC coefficients
are more than threshold value T
v
, then that block is a
non-sensitive JPEG block.
Let the DC coefficient be denoted as DC
i
(where,
i = 0), the AC coefficients as AC
i
, (where, i =
1, 2, · · · , n − 2, n − 1, n), and the threshold value T
v
. If
a JPEG block has AC coefficients (i.e., both nonzero
and zero) as follows [16 1 0 0 0 -2 1 0 0 -1 2 EOB],
Figure 1: Block diagram of the encoding phase.
we denote them as DC
0
= 16, AC
1
= 1, AC
2
= 0, AC
3
=
0, AC
4
= 0, AC
5
= -2, AC
6
= 1, AC
7
= 0, AC
8
= 0, AC
9
= -1, AC
1
0 = 2, and the end-of-block (EOB) marker
follows. The nonzero AC coefficients are easily iden-
tified, where there are 5: AC
1
= 1, AC
5
= -2, AC
6
= 1,
AC
9
= -1, and AC
10
= 2. If the value T
v
is 3, then the
number of nonzero AC coefficients in this example is
more than T
v
, which means that this JPEG block is a
non-sensitive block (see Figure 2). Again, in another
example with zigzag-scanned JPEG coefficients [32 5
0 0 0 2 EOB], we can denote them as DC
0
= 32, AC
1
= 5, AC
2
= 0, AC
3
= 0, AC
4
= 0, AC
5
=2, and EOB. The
number of nonzero AC coefficients is 2: AC
1
= 5 and
AC
5
= 2. Note that this block is sensitive when T
v
is 3
(see Figure 3) by the definition of sensitive and non-
sensitive blocks. The zero coefficients can be shifted
in the non-sensitive blocks to hide data. In addition,
magnitude of the nonzero coefficients of the sensitive
blocks can be modified. For the modification of coef-
ficients, another threshold value T
c
is used. Threshold
values T
v
and T
c
are set according to the embedding
capacity and image quality required.
2.2 Shifting Nonzero AC Coefficients
On basis of the T
v
value, the proposed method shifts
T
c
number of nonzero AC coefficients to make either
even or odd number of zeros in between two nonzero
coefficients in order to hide data into the non-sensitive
JPEG block. This shifting operation results in the
number of zero AC coefficients while nonzero coef-
ficients are unchanged. If the number of AC coeffi-
cients in between nonzero AC coefficients is odd and
the message to hide is ”1”, this method does not need
to make any change. But if the number of zero co-
efficients is odd but the message to hide is ”0”, this
method has to make the number of zero coefficients
even by either removing or inserting one zero so that
the next nonzero AC coefficient shifts from its orig-
inal position either to the left or right, respectively.
There are two more cases to make four possible cases.
The other two cases are similar to the previous two
cases in nature.
The overall four cases are summarized in Subsec-
tion 2.3. For the decoder, odd or even number of ze-
ros indicated the hidden message information. The
following block [16 1 0 0 0 -2 1 0 0 -1 2 EOB] is
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
146

Figure 2: A non-sensitive original JPEG block (a), the
zigzag scanned array of the non-sensitive block (b), and the
changed array after embedding binary data ”01” (c).
a non-sensitive block. Embedding of the secret mes-
sage ”01” into this non-sensitive block changes like
[16 1 0 0 0 -2 1 0 0 -1 0 2 EOB] (see Figure 2). Note
that one zero is forcefully inserted in between AC
9
and
AC
10
. Therefore, the position of the last nonzero AC
coefficient (i.e., 2) has to be shifted to right and will
have new position AC
11
.
2.3 Modifying Magnitude Nonzero AC
Coefficients
Magnitude modification is applied to the sensitive
blocks. The magnitude of the first T
c
nonzero coef-
ficients is modified by a very simple rule. While the
hidden bit is 0 and the magnitude value of nonzero
AC coefficient is odd, then the method reduces or in-
creases the magnitude value by 1 in order to make it
even. Similarly, when the method has to hide 1 and
the magnitude is even, this method increases or re-
duces the magnitude by 1 to make it odd. Always the
magnitude value 0 was skipped for modification.
The following block [32 5 0 0 0 2 EOB] is a sen-
sitive block. There are two nonzero AC coefficients:
AC
1
= 5 and AC
5
= 2. After embedding the block be-
comes either like [32 4 0 0 0 1 EOB] or [32 6 0 0 0 3
EOB].
2.4 Embedding Algorithm
Embedding algorithm of this paper is summarized as
follows:
Encoder
(1) Separate the sensitive blocks by T
v
.
(2) If the block has less AC coefficients than or equal
to T
v
, this block is sensitive, and otherwise, non-
sensitive.
Figure 3: A sensitive JPEG block (a), the zigzag scanned
array of the sensitive block (b), and the changed array after
embedding binary data ”01” (c).
(3) Change the magnitude values in the sensitive
block (maximum number of changes is not more
than T
c
).
(a) If the message to hide is 0 and the nonzero
coefficient magnitude is odd, make it even by ei-
ther increasing or reducing the magnitude value
by 1.
(b)If the hidden message is 1 and the number
of zeros between two nonzero AC coefficients is
even then to make it odd either one exist-ing zero
was deleted or one extra zero was added.
(4) Change the number of zeros in between the
nonzero AC coefficients (maximum changes not
more than T
c
).
(a) If the hidden message is 0 and the number
of zeros between two nonzero AC coefficients is
odd then to make it even either one extra zero was
added or one existing zero was deleted.
(b) If the message to hide is 1 and the
nonzero coefficient magnitude is even, make it
odd by either increasing or reducing the magni-
tude value by 1.
Decoder The decoding algorithm is given bellow.
(1) Separate sensitive blocks from non-sensitive
blocks by T
v
.
(2) In sensitive block, the magnitude values of T
c
nonzero coefficients are checked to see if they are
odd or even. The odd magnitude values are repre-
sented by 1 and even numbers are represented by
0.
(3) In non-sensitive blocks, the number of zeros in be-
tween last T
c
nonzero coefficients are counted. If
the number is either odd or even, then the hidden
message is either 1 or 0, respectively.
AN IMPROVED STEGANOGRAPHIC METHOD
147
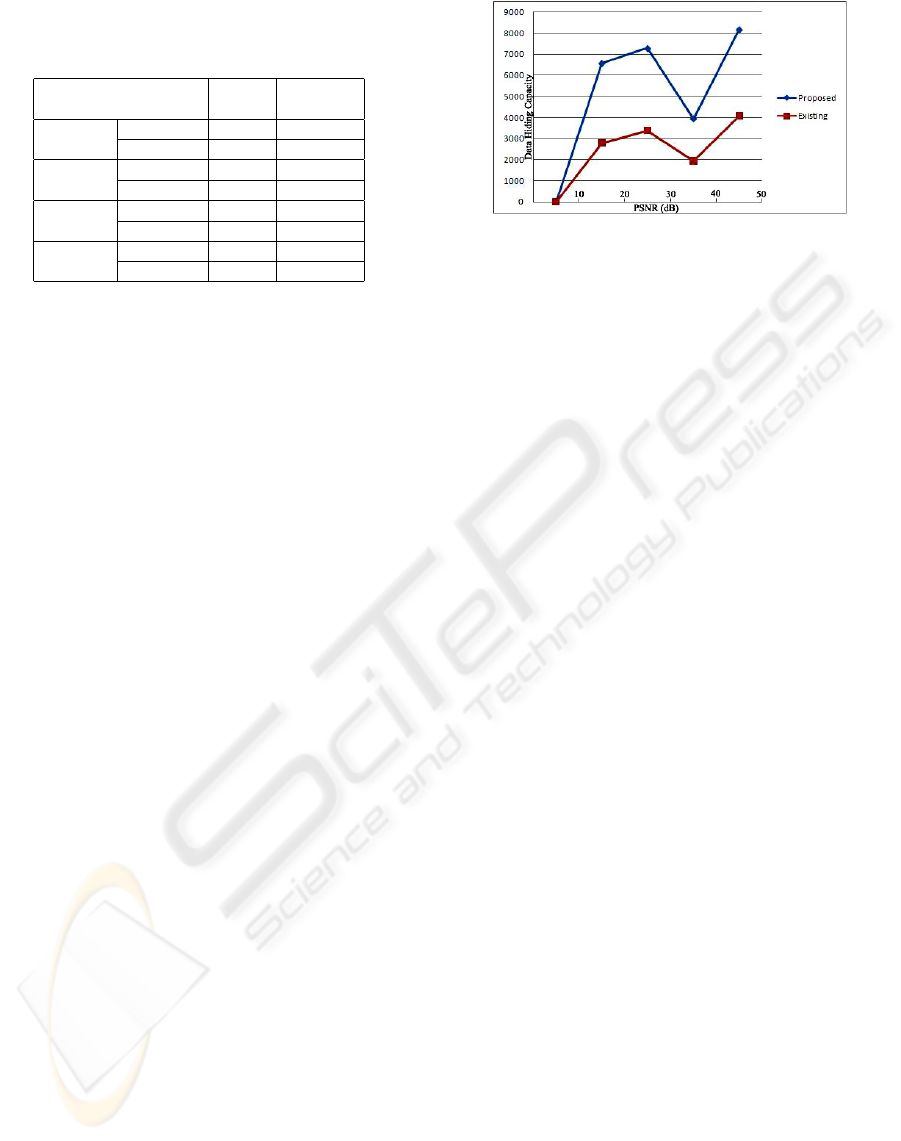
Table 1: Performance over Hiding Capacity, Comparison
between [1]:(Amiruzzaman and Kim, 2008) and the pro-
posed method.
PSNR Capacity
[dB] [bits]
Lena Proposed 38.46 6,558
[1] 39.99 2,798
Barbara Proposed 32.59 7,277
[1] 33.19 3,372
Goldhill Proposed 34.73 3,936
[1] 36.38 1,932
Baboon Proposed 30.61 8,161
[1] 30.19 4,064
3 EXPERIMENT AND
DISCUSSION
3.1 Results
Implementing the proposed method is simple and
easy. For the encoder and decoder, the proposed
method was tested on four images. Performance of
the data hiding methods is compared with different
threshold values. The sample images are 512x512
in size and have 4,096 8×8 DCT blocks. With dif-
ferent threshold values, various numbers of sensitive
and non-sensitive blocks are obtained to hide data.
The threshold values are used to control the capac-
ity as well as image quality (i.e., PSNR). In best
case of Lena image, while T
v
=3 and T
c
= 3, 6,558
bits of data can be hidden with 38.46 dB of PSNR
value (see Table 1). Due to change of both zero co-
efficients and nonzero coefficients, image quality is
slightly worse than the other method (Amiruzzaman
and Kim, 2008), while embedding capacity is more
than twice.
Since Baboon image has many nonzero AC coeffi-
cients due to its rich high-frequency components, the
hiding capacity is significantly higher than other im-
ages. Note that the embedding capacity of Baboon
image is 8,161 bits with 30.60 dB. Barbara image can
hide 7,277 bits of data with 32.58 dB; In any case, im-
age quality is slightly worse, but embedding capacity
is more than twice. Change in number of zero coeffi-
cients does not affect the histogram. However, mag-
nitude change of nonzero coefficients produces un-
noticeable change in the histogram (see Appendix).
By mixing two different methods, the effect of F3-
like method which modifies the nonzero coefficients
in sensitive blocks is attenuated much.
Figure 4: Comparison with an existing method (Amiruzza-
man and Kim 2008) and the proposed method.
3.2 Discussion
The reason of shifting nonzero coefficients from the
last places to forward positions is very simple. The
leftmost coefficient values are more important than
the rightmost in the zigzag scanned array. As a re-
sult, shifting direction from the last to the first makes
less distortion in JPEG-compressed images. It is ob-
vious that Inserting or removing at least one zero co-
efficient affects image quality much more. It causes
the change of at least two coefficients: one zero co-
efficient and another nonzero coefficient. In Figure 2,
after data hiding, AC
10
is changed from 2 to 0, and,
AC11 from nothing to 2. Thus, image quality has to
be much worse than just changing magnitude. Mag-
nitude change produces worst case magnitude differ-
ence by 1. On the other hand, difference before and
after data hiding is 2 for AC
10
, and 2 for AC
11
.
Similarly, the reason of modifying the magnitude
values from the first places is that they are close to
the DC value and have rich low-frequency compo-
nents. Quantization coefficients closer to the DC co-
efficient are smaller than those opposite to it. Thus,
the same difference in nonzero coefficients produces
much larger error if they are far from the DC coef-
ficient. It is obvious that two data hiding methods
used in this paper compensate each other by making
up the weakness each method has. One of cons of the
changes in number of zero coefficients is relatively se-
riously downgraded image quality. On the other hand,
its advantage is that this method does not change his-
togram at all after data hiding. Change in nonzero
coefficients leaves a trace of data hiding in the his-
togram. However, this method slightly degrades the
image quality. Pros and cons of two techniques are
fully exploited in this paper to achieve high embed-
ding capacity with low image degradation. Figure 4
shows that the proposed method is always better than
an existing method (Amiruzzaman and Kim, 2008) in
terms of embedding capacity. As is mentioned above,
however, image quality is slightly worse that the ex-
isting method.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
148
4 CONCLUSIONS
The proposed method provides significantly higher
embedding capacity with slightly worse image quality
in comparison with a method of Amiruzzaman et al.
(Amiruzzaman and Kim, 2008). In terms of security
issue, this method is a little weaker but still can pro-
duce almost the same histogram and distortion is not
significant. For the future work, optimization can be
used to develop this method to improve performance
and security issue. Many variations are possible in
combination of two methods. New combination can
improve performance much
ACKNOWLEDGEMENTS
This work was in part supported by Information Tech-
nology Research Center (ITRC), by the Ministry of
Information and Communication, Korea.
REFERENCES
Amiruzzaman Md. and Kim H. J. (2008). Selective block
steganography. In Proceedings of the 3rd Interna-
tional Joint Workshop on Information Security and
Applications, pp. 123-133.
Fridrich J., Goljan M., and Hogea H. (2002). Attacking the
Out-Guess. In Proceedings of the ACM Workshop on
Multimedia and Security, pp. 967-982.
Fridrich J., Goljan M., and Hogea H. (2003). Steganalysis of
JPEG image: Breaking the F5 algorithm. In Lecture
Notes in Computer Science, vol. 2578, pp. 310-323.
Fridrich J. (2004). Feature-based steganalysis for JPEG im-
ages and its implications for future design of stegano-
graphic schemes. In Lecture Notes in Computer Sci-
ence, vol. 3200, pp. 67-81.
Provos N. (2001). Defending against statistical steganal-
ysis. In Proceedings of the 10th USENIX Security
Symposium, pp. 323-335.
Sallee P. (2004). Model-based steganography. In Lecture
Notes in Computer Science, vol. 2939, pp. 154-167.
Sallee P. (2005). Model-based methods for steganography
and steganalysis. In International Journal of Image
and Graphics, vol. 5, no. 1, pp. 167-190.
Solanki K., Sarkar A., and Manjunath B. S. (2007). YASS:
Yet another steganographic scheme that resists blind
steganalysis. In Proceedings of the 9th International
Workshop on Information Hiding, Saint Malo, Brit-
tany, France, pp.16-31.
Westfeld A. and Pfitzmann A. (2000). Attacks on stegano-
graphic systems In Lecture Notes in Computer Sci-
ence, vol. 1768, pp. 61-75.
Westfeld A. (2001) F5: A steganographic algorithm: High
capacity despite better steganalysis. In Lecture Notes
in Computer Science, vol. 2137, pp. 289-302.
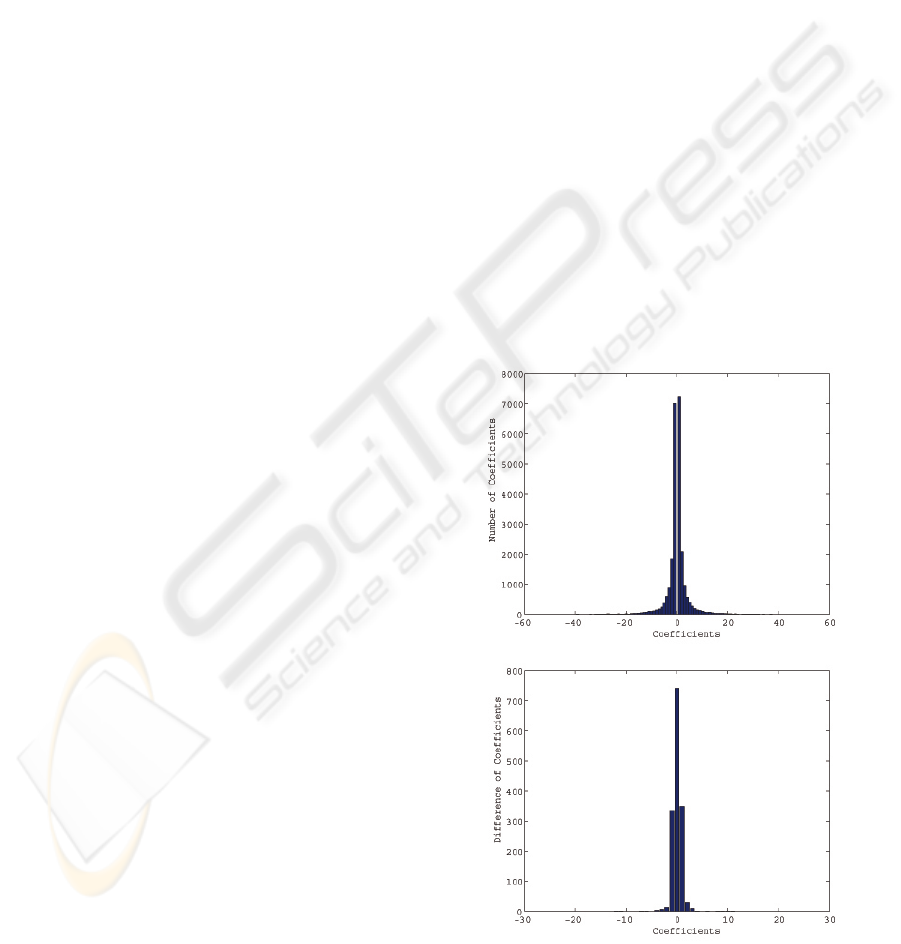
APPENDIX
After hiding data by the proposed method, small
changes are observed in the histogram of the stego im-
age compared with original image. Two graphs of his-
togram for original image and the difference be-tween
original and stego images. It is observed that the dif-
ference is almost negligible, and, hence, the stego im-
age is relatively secure due to its capability to keep
almost the same histogram. Histogram of the original
image compressed by JPEG has a Cauchy-like distri-
bution as shown in Figures 5 and 6. Difference in the
histogram is almost equal to the number of total non-
zero coefficients changed in the sensitive blocks. By
adjusting the threshold values T
v
and T
c
, histogram of
the difference can be controlled. Note that the differ-
ences between histograms depend on images: Baboon
image produces very little differences while Lena rel-
atively significant differences.
Figure 5: Histogram of the original Lena image (top) and
that of the difference between original and stego images
(bottom).
AN IMPROVED STEGANOGRAPHIC METHOD
149
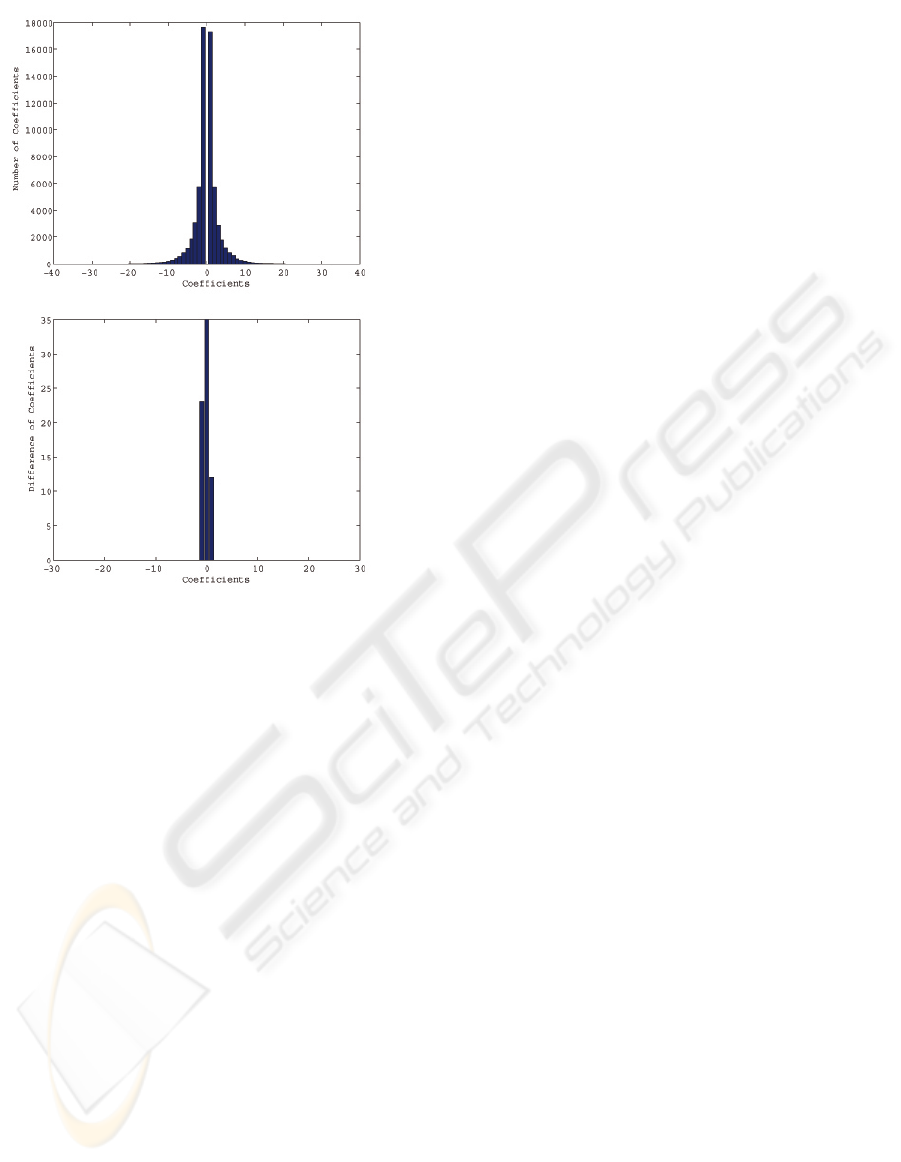
Figure 6: Histogram of the original Baboon image (top)
and that of the difference between original and stego im-
ages (bottom).
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
150
