REBEL

Reconﬁgurable Block Encryption Logic

Mahadevan Gomathisankaran

Department of Electrical Engineering, Princeton University, Princeton, New Jersey, U.S.A.

Ka-Ming Keung, Akhilesh Tyagi

Department of Electrical and Computer Engineering, Iowa State University, Ames, Iowa, U.S.A.

Keywords:

Block Cipher Function.

Abstract:

REBEL is a ﬁestel network based block encryption function which uses reconﬁgurable gates instead of substi-

tuition boxes. This novel design approach has many advantages such as the key size can be much greater than

the block size, security can be reduced to boolean square root problem (Kutz, 2004) and resitant to known

cryptanalytic attacks. The implementation results show that our proposed design can better AES in every

design parameter at the same time providing much higher security.

1 INTRODUCTION

Block cipher function is the fundemental building

block of the encryption systems. The security of

block cipher functions is directly related to its key

size. This is one of the primary reasons for the NIST’s

AES proposal to replace DES. The key size of DES

(56 bits) was becoming too weak compared the con-

temperorary computing power. The trend of increase

in the computing power is not going to change. The

transistor size reduction together with multi-core ap-

proach will keep the rate of this increase approxi-

mately constant. Thus in the near future we can ex-

pect that 128 (or even 256) bits of keys becoming in-

sufﬁcient. Thus we need to research on new block

cipher functions which can provide much larger key

sizes (for example: 512, 1024 bits). The block size of

these algorithms determine the latency of the encryp-

tion systems and hence it would be advantageous if

the block size can be small (64 bits) compared to the

key size.

Conventional block ciphers (National Bureau of

Standards, 1999; National Bureau of Standards, 2001;

Anderson et al., 2000) derive their security from an

embedded secret, more commonly referred to as a

key. One of the inputs, key, in each round is secret

whereas the round functions themselves are public.

The secret, however, is combined with the state in a

limited way, as an xor, during a round. We propose

a simple yet novel approach wherein the round func-

tions themselves become the secret, while the func-

tion schema is a publicly published algorithm. The

intuition is to use reconﬁgurable gates as round func-

tions and deﬁne their conﬁgurations as the secret (or

key). Hence the complexity of such a cryptographic

function is derived from the fact that almost all of the

round processing is driven by the secret (truth tables).

In a traditional block cipher, the secret is combined

with the state with an xor as one of the steps in the

round. This xor step is susceptible to linear model-

ing of the secret and input/output relationship. When

the secret is used as a Boolean gate truth table, it is

inherently non-linear.

The key advantages of our design approach are:

1. Key size is much greater than the block length.

This allows to higher security guarantees without

having to increase latency of cipher operation.

2. Smaller block lengths suite well for instruction

level encryption when placed in-line into a pro-

cessor pipeline (Lie et al., 2000; Suh et al., 2003).

3. Area and time efﬁcient hardware implementation

reduces the security processing overhead drasti-

cally.

Reconﬁgurable S-boxes have been proposed and

used in GOST (GOS, 970 ) and TREYFER (TRE,

1997) encryption algorithms. GOST 28147-89 is a

Soviet and Russian government standard symmetric

312

Gomathisankaran M., Keung K. and Tyagi A. (2008).

REBEL - Reconﬁgurable Block Encryption Logic.

In Proceedings of the International Conference on Security and Cryptography, pages 312-318

DOI: 10.5220/0001922003120318

 SciTePress

key block cipher. GOST deﬁnes the S-Boxes to be

secret but does not use the key bits to choose the S-

Boxes. The GOST philosophy is to pre-determine S-

Boxes between communicating parties. TREYFER

is a block cipher/MAC designed in 1997 by Gideon

Yuval. TREYFER has single 8x8 S-Box which is

deﬁned by the secret key. Due to the simplicity of

its key schedule, using the same 8 key bytes in each

round, Treyfer was one of the ﬁrst ciphers shown to

be susceptible to a slide attack (Biryukov and Wag-

ner, 1999). This cryptanalysis is independent of the

number of rounds and the choice of S-box.

Results. Following are the key contributions of this

paper.

• A novel block encryption algorithm whose secu-

rity is reducible to Boolean Matrix Square root

problem

• Performance characterization of the algorithm in

Software, ASIC and FPGA

2 INTUITIVE DESIGN

Pseudorandom functions form the fundamental build-

ing block of a ﬁestel network based encryption func-

tion. Pseudorandom function (PRF) should exhibit

two fundamental properties namely efﬁcient evalua-

tion and effective similarity. Efﬁcient evaluation re-

quires that the PRF be realizable with a poly sized

circuit (both time and size) and effective similarity

requires that the PRF should exhibit similar charac-

teristics as a truly random function for any poly sized

(both time and space) observerd. So the ﬁrst step is to

design a PRF.

Efﬁcient Evaluation. Let N be the block size of the

PRF. Let S

be the set of all N × N functions (gates),

then |S

| = 2

. In order to satisfy the efﬁcient eval-

uation criteria we need to form a subset G

such that

every gate g ∈ G

is realizable in poly-time and poly-

space of N. Let m be such that n = O(logN) and

q =

. Then any gate g ∈ S

, the set of all n× n gates,

is representable with n2

bits. If we design the set G

with q gates chosen from S

then every gate g ∈ G

representable with N2

= O(N) bits.

Effective Similarity. Effective similarity require-

ment can be further broken down into symmetry and

similarity.

• Symmetry requires that every output bit is inﬂu-

enced by every input bit uniformly.

i →

q−1

j →

q−1

q−2

q−1

q−3

q−2

q−1

Figure 1: Construction of

• Similarity requires that any differential input

causes output differential effectively similar to the

universalset. In other words the output bits should

switch with a probability very close to

Let

f represent the N × N gate realized by the q,

n× n gates. Let γ

represent the i

n× n gate where

0 ≤ i ≤ q − 1. There are q gates and each of these

gates are chosen independently (remember key bits

are chosen uniformly at random and key bits form the

conﬁguration bits for these q gates). Let X and Y be

the input and output to

f. Let x

and y

be the i

group

of n bits of X and Y respectively, i.e., x

= bits i∗ n to

i∗ n+ n− 1 of X and y

= bits i∗ n to i∗ n+ n− 1 of

The ﬁrst design goal is to achieve symmetry. The

simplest way to achieve this goal is by passing every

input group through every one of the q gates. So we

deﬁne y

as follows,

j=1

(i+ j)%q

)

Figure 1 shows this construction diagramatically. In

this ﬁgure every circle represents the n 7→ n gate. All

the gates in the j

row are fed with the input X

. The

outputs of all the gates in the i

column are XORed

to produce the output Y

This structure ensures the symmetry property with

respect to both input and the key bits. Also the use of

XOR gate ensures that the inﬂuence of every γ

and x

on the output is equal. Such a gate

f has some nice

properties. It can produce all N bit symbols with equal

probability. The collision probability, that is two dif-

ferent inputs producing the same output symbol, is

equal to that of the universal set. In other words,

f(x) =

f(x

′

)|x 6= x

′

] =

Security. We want to base the security of our design

on a hard problem. The problem that is of interest to

REBEL - Reconfigurable Block Encryption Logic

313

us is the Boolean Matrix Square Root problem which

is proven to be NP-Complete by Martin Kutz (Kutz,

2004). Kutz (Kutz, 2004) refers to this problem as

digraph root problem for the kth root for k ≥ 2. Given

a graph G, the problem is to ﬁnd its factors such that

G(X) = F(F(X)) or to determine that such a factor F

(square root) exists. Kutz shows that this problem is

NP-complete (Theorem 1, (Kutz, 2004)).

We can model the function

f as a 2

×2

boolean

matrix where a bit in the i

row and j

column (b

i, j

)

is set to 1 if

f(i) = j. If we compose

f twice and

use this composition

as the round function in LR-

network then any security question related to con-

struction could be answered only if a solution to the

Boolean Matrix Square Root of

can be found.

3 THEORY

3.1 Notations

In the following deﬁnitions x and y are binary strings

of arbitrary but equal lengths, i and j are non-negative

integers.

• % represents the modulus operator

• Let I

be the set of all n bit binary strings i.e., I

= {0,1}

• Let BIT(x, i) be the i

bit of x counting from left

(wlog)

• Let BITS(x, i, j) = (BIT(x, i),BIT(x,i + 1),

...,BIT(x, j)) where j ≥ i

• Let GRP(x, i, n) = BITS(x,i·n,i·n+n−1) i.e., the

group (from left end) of n bits of x (wlog)

• Let γ

k,l

be the I

7→ I

reconﬁgurable gate

• Let γ

k,l

[tt] be the truth table bits of γ

k,l

and |tt| =

l · 2

3.2 Function

Construction 1.

f : X × κ 7→ Y where X,Y ∈ I

and

κ ∈ I

(N+n)2

f is constructed from

+1, γ

n,n

component gates,

where n = O(logN). Let q =

. Let γ

n,n

be the

reconﬁgurable gate, where 0 ≤ i ≤ q and the

truth table is assigned as γ

n,n

[t] = GRP(κ, i,n2

). Let

= GRP(X,i,n) and Y

= GRP(Y,i,n). Let

repre-

sent the function realized by conﬁguring the reconﬁg-

urable gates with the key bits κ. Then the output Y is

deﬁned as follows.

Then,

q−1

j=0

n,n

(i+ j)%(q+1)

)

Note that the construction of

f deﬁned above dif-

fers from the intuitive construction given in Section 2.

In Section 2 we had used only q, γ

n,n

gates, whereas

in Construction 1 we have used q+ 1 gates. This en-

sures that every Y

differs from every other Y

(i 6= j)

by at least one gate γ

n,n

, thereby making Y

and Y

independent.

In the following discussions the properties of the

function

f refers to the properties of the set of all the

gates realized over the universe of conﬁguration bits

κ.

3.2.1 Properties of

Two important relevant properties of any Boolean

function including

f are controllability and observ-

ability. These are similar to the notion of controlla-

bility & observability in VLSI testing. In plain terms,

given the ability to control the input to

f what proper-

ties of the output can be controlled. Similarly, given

the ability to observe the output what properties of the

input can be inferred. These two properties are essen-

tial building blocks of any cipher function. The dis-

tinction between controllability and observability ex-

ists only when the internal nodes of a function block

are considered. In the context of

f, we assume that the

adversary can directly access only the primary input

X and primary output Y. In such a case, both notions

become identical.

Deﬁnition 3.1 (Controllability/Observability). Con-

trollability/Observability refers to the maximum

probability with which any output bit can be con-

trolled by controlling the inputs to a gate. Formally,

Controllability/Observability(

f) =

max

0≤i, j<N



δY

δX



. The Boolean derivative

δY

δX

is deﬁned in the standard way as (Y

)

⊕ (Y

)

where (Y

)

and (Y

)

denote the Shannon cofactors

of Y

with respect to X

and it’s complement.

Symmetry.

f exhibits the followingsymmetry. Every

output bit is equally probable to switch for any differ-

ential input pair. This property is easy to observe as

every input bit has the same level of inﬂuence on ev-

ery output bit. More formally, the controllability of

each input/output bit pair is the same averaged over

the entire gate space: Σ

κ∈ I

(N+n)2



δY

δX



is the same

for all 0 ≤ i, j < N.

Strength of

. In

, let X be the input, Y be

the output, and Z be the intermediate output, i.e.,

SECRYPT 2008 - International Conference on Security and Cryptography

314

Figure 2: Construction of R

Z =

f(X), Y =

(X) =

f(Z). Due to symmetry

property (Property 3.2.1), no static bias model can

be developed. Biases, however, do exist in speciﬁc

instantiated keys κ, which an adversary can attempt

to model through multiple differential input experi-

ments and their effects on the output. Construction

takes away that opportunity. The observable output Y

does not provide any information about the switch-

ing (or differential state) of any particular bit of Z

(since from the static model, all of them are equally

probable). The only means to extract the information

about the secret conﬁgurations of the gates seems to

be the brute force search. Alternately, if the adver-

sary could factor

into

f, then a differential con-

trollability/observability attack becomes more feasi-

ble. Martin Kutz (Kutz, 2004) shows that such factor-

ing is NP-Complete. NP-Completeness of

problem

does not guarantee that every instance of the problem

is hard or even that an average instance of the problem

is hard. But we do believe that this problem is a hard

problem on the average. This intuition is based on the

prevalent belief that prime factoring of an integer is

difﬁcult on average.

3.3 REBEL Cipher Function

Construction 2. R : X × κ 7→ Y where X,Y ∈ I

and κ ∈ I

(N+n)2

R is a LR-network with four levels as shown in

Figure 2. Let R

represent the REBEL cipher func-

tion whose key is κ. R

has four levels. The pseudo-

random function associated with ﬁrst and last levels

. The middle level pseudorandom function is

This design choice ensures that every internal node is

neither observable nor controllable by the adversary.

In REBEL encryption and decryption algorithms are

the same.

3.3.1 Key Space

The key κ of R is nothing but q + 1 n 7→ n gates cho-

sen at random from the universal set. Each n 7→ n

gate can be further considered as n n 7→ 1 gates thus

making the key comprising of N + n n 7→ 1 gates.

In order to strengthen the key space we remove lin-

ear and the constant gates from the universal set.

Let K

be the set of valid n 7→ 1 gates then |K

| =

− 2

n+1

− 2. Let K be the set of valid keys for R

then K = {K

}

N+n

4 CRYPTANALYSIS

In this section we investigate the resilience of REBEL

toward the well known cryptanalysis methods. First

we will show the class of attacks which use the invari-

ance property of system, i.e., the idea of these attacks

is to ﬁnd the properties of the system which are not

dependent or least dependent either on the secret or

the input.

4.1 Linear Cryptanalysis

Linear cryptanalysis is a general form of cryptanal-

ysis based on ﬁnding afﬁne approximations to the

cipher function. The technique (Matsui, 1993) has

been applied to attack ciphers like FEAL (Miyaguchi,

1990) and DES (National Bureau of Standards, 1999).

Linear cryptanalysis exploits the high probability of

occurrences of linear expressions involving plaintext,

ciphertext, and sub-key bits. This attack becomes pos-

sible on the conventional cipher function design as

the key bits are primarily XOR’ed with round inputs.

The linear approximations of known components (S-

boxes) in the system further aid the analysis. In the

case of REBEL none of these required conditions are

present. Every γ

n,n

gate is chosen randomly from the

set of nonlinear gates.

4.2 Differential Cryptanalysis

Differential cryptanalysis (Biham and Shamir, 1991)

exploits the property of difference being propagated

from input to the output of the cipher function. This

attack again requires the properties of the known com-

ponents in the system (S-boxes) in order to estimate

the difference propagation probabilities. In REBEL

such an analysis is not possible as there are no known

components in the system. A variant to this attack

is impossible difference attack (Biham et al., 2005)

which again uses the principle of identifying differ-

ences that do not propagate from input to output.

4.3 Boomerang Attack

This attack (Wagner, 1999) relies on the difference

analysis of round function properties and existence of

some block in the system which is independent of the

REBEL - Reconfigurable Block Encryption Logic

315

input to cipher function. This can be thought of as

meet-in-the middle version of differential cryptanaly-

sis. Again REBEL is resistant as there are no blocks

(gates) in the system that is either independent of key

or the input.

4.4 Sliding Attack

This attack (Biryukov and Wagner, 1999) exploits the

weakness of the round functions. It assumes that

given two pairs P,C and P

′

such that P

′

= f(P) and

′

= f(C), the round function can be deciphered or at

least a signiﬁcant fraction of key bits can be extracted.

These attacks once again use the property of round

functions being built using some known components

(S-boxes) and key bits being used only in XOR oper-

ations.

In REBEL ﬁrst and last round functions are f

Section 3.2.1 argues why such round function can-

not be deciphered given a polynomially many input

output pairs. Hence sliding attack is also ineffective

against REBEL.

5 IMPLEMENTATION

In this section we discuss the REBEL cipher function

R implementation for N = 32 bits. The major ad-

vantage of REBEL is that the block size can be much

smaller than the key size. We choose n = 4 as it sat-

isﬁes the requirement that n ≤ logN. Also, reconﬁg-

urable gates of n > 4 are impractical. Thus we get

576(|κ| = (N +n)2

) key bits or conﬁguration bits for

the function

f. We implemented the REBEL cipher

function R with a block size of 64 bits and key size

of 576 bits both in software and hardware.

5.1 Software

We implemented the software version in C language.

Our optimization goal was performance. Hence we

traded area or in software memory space to increase

the performance. In

f every 4 bits of input is oper-

ated on by 8 4x4 LUTs. So we created 64 such LUTs

so that each input group can be operated on indepen-

dently. Thus we require a memory space of 512 bytes.

This is less than 0.025% of a L2 cache of 2MB which

is very common in contemporary processors.

The conﬁguration table in memory is laid out as

a two dimensional array of 16 rows and 8 columns of

32 bits. The column signiﬁes the input group (input to

f). The action of choosing i

row in a j

column is

equivalent to the operation of passing the X

through

eight 4x4 LUTs. Thus the function

f is implemented

with 8 memory lookups and 7 XOR operations of 32

bits. In total R takes 94 operations to produce the

result of 8 bytes. Thus we can achieve a rate of 11.75

cycles per byte assuming one operation per cycle.

We simulated the algorithm in a x86-64 Intel Pen-

tium D CPU 3.20GHz machine with a 2MB L2 cache.

The program was compiled with gcc-4.1.0 with opti-

mization level 3. We did 1 Billion encryptions (or

decryptions) to estimate the performance. On the av-

erage it took 36.08 seconds to perform 1 Billion en-

cryptions. Thus REBEL can achieve a rate of 1.77

Gbps or 14.432 cycles per byte. This is very close the

theoretical minimum of 11.75 cycles per byte. The

fastest known implementation of AES takes 15 cy-

cles per byte. The eStream (eStream, a) project lists

AES performance as an random number generator in

counter mode. The Pentium 4 ﬁgures (eStream, b) of

AES show that it takes 17.81 cycles per byte. REBEL

outperforms AES-128 even though the key size is 4.5

times that of AES.

5.1.1 Heuristic Testing

Table 1: Test Suites Tested on REBEL Counter Mode.

Test Suite Parameters # Statistics Results

Small Crush Standard 15 PASS

Crush Standard 144 PASS

Big Crush Standard 160 PASS

Alphabit 2

bits 17 PASS

Rabbit 2

bits 40 PASS

FIPS-140-2 20000 bits PASS

Any Encryption function can be used as a Ran-

dom Number generator in counter mode. We can

heuristically test the encryption algorithm by test-

ing for randomness in the output stream. We used

the TestU01 (L’Ecuyer and Simard, 2007) to test the

randomness of the bit-stream generated by REBEL

in counter mode. We tested for p-values within the

boundary [10

−4

,1 − 10

−4

]. We considered any p-

value lying outside this boundary as a failure. Table 1

lists the test suites and the results. Standard param-

eters in Table 1 refers to inbuilt test parameters of

test suites. In all, 376 statistical tests were performed

and REBEL counter mode passed all of them. We re-

peated all these tests 10 times (except for Big Crush)

to increase the conﬁdence level of the test results and

all of them passed. This heuristically proves the fact

that the

f is a pseudo-random function and R is a

pseudo-random permutation function.

SECRYPT 2008 - International Conference on Security and Cryptography

316

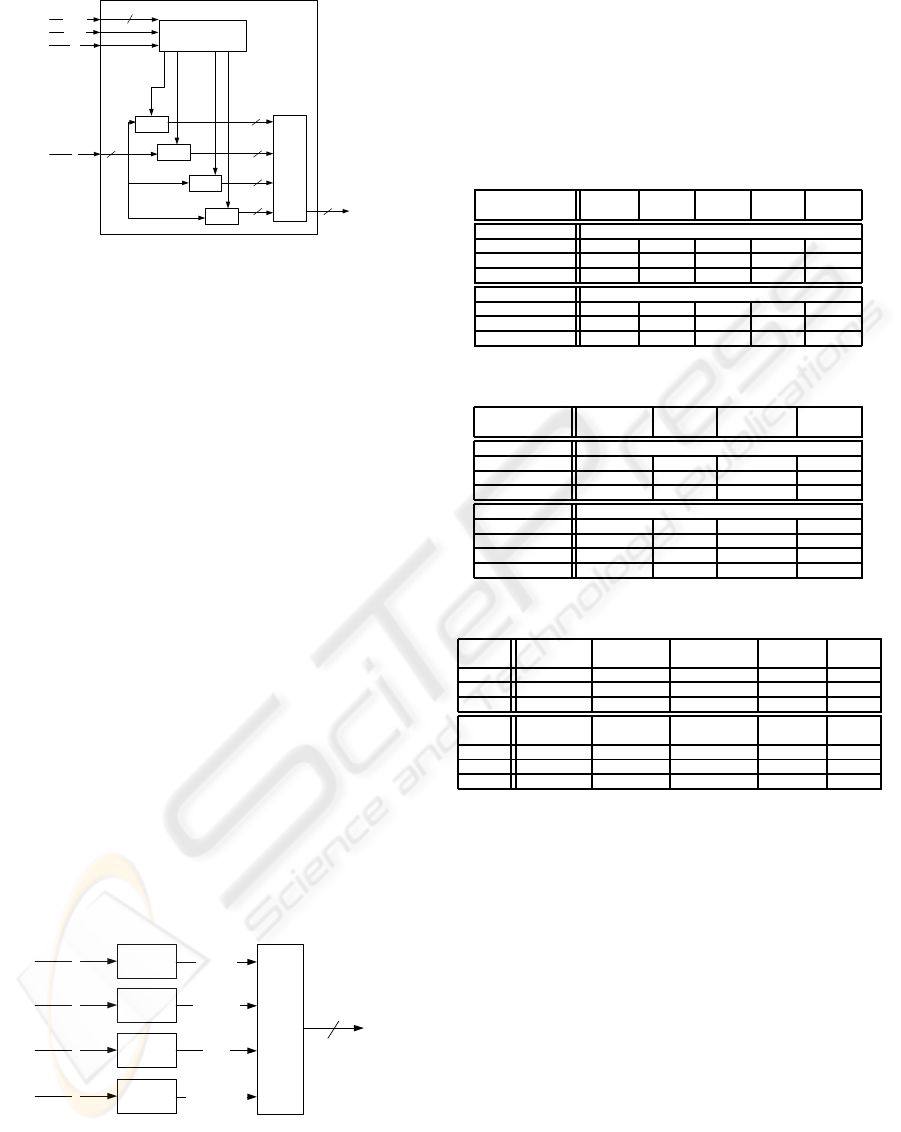
Rebel

clk

config

datain

Config Bits

...

XOR

CB[511:0]

[575:64]

CB[575:448,383,]

Figure 3: ASIC implementation of

f (Register)).

5.2 Hardware Implementation and

Result

We implement REBEL in ASIC and FPGA to mea-

sure its area, power and throughput. There are two

ASIC REBEL designs. REBEL(reg) uses registers

to store the key while REBEL(sram) uses SRAM to

store the key. The REBEL is implemented in VHDL,

synthesized by Cadence Physically Knowledgeable

Synthesis and placed and routed by Cadence En-

counter with TSMC 130nm and 65nm technologies.

The design of

f(N=32, n=4) is shown in Fig-

ure 3. The 576-bit conﬁguration bit memory stores

the REBEL’s key. REBEL takes 18 cycles to store

a new key. The memory provides 512 conﬁguration

bits for each function F. Function F implements 8,

64-to-4 multiplexers signifying 8 4 7→ 4 LUTs. Thus

64 bits of conﬁguration signiﬁes a 4x4 LUT. The con-

ﬁguration bits are rotated by 64 bits and fed to the

multiple instances of F. The XOR unit XORs the out-

puts from all function F units and produces output Y.

The SRAM version is pretty similar to the software

version. The SRAM has 8 blocks. Each block has 16

rows and 32 bits. All these blocks are accessed paral-

lely. We used CACTI to estimate the delay, area and

energy parameters of the SRAM.

LUT

GROUP0

XOR

R(31:0)

LUT

GROUP1

R(63:32)

LUT

GROUP..

R(...)

LUT

GROUP7

R(255:224)

Figure 4: FPGA Implementation of

The FPGA REBEL is shown in Figure 4. The con-

ﬁguration bits are stored in the LUT group. The 32-bit

input X selects a 32-bit wide output R from the eight

LUT groups. Each LUT group contains 32 LUTs.

The 32-bit wide X is divided into 8 groups(X[3 :

0],X[7 : 4]...). Each group is used to select 4 out-

put bit R from 4, 4-LUTs respectively. Finally an

XOR unit XORs all 32-bit LUT groups’ output and

produces output Y.

Table 2: Data Table A.

ns Gbit/s mW Cycles

Type Area Period Tput Power Cycles

130nm

Rebel(reg) 98300 2.4 4.44 56.4 6

Rebel(sram) 89468 1.72 6.20 76.92 6

AES(Opencore) 158290 4 3.2 90.61 10

65nm

Rebel(reg) 26200 1.4 7.61 26.99 6

Rebel(sram) 22474 1.03 10.37 30.77 6

AES(Opencore) 43049 2 6.4 45.56 10

Table 3: Data Table B.

J/bit um

∗ us kbit/um

/s nJ ∗ um

Type Energy/Bit A*Time Tput/A PAT

130nm

Rebel(reg) 12.69 236 45.2 13310

Rebel(sram) 12.39 153.71 69.4 11823

AES(opencore) 28.32 633.16 20.22 57373

65nm

Rebel(reg) 3.54 36.72 290.5 991.01

Rebel(sram) 2.97 23.1 461.69 710.9

AES(opencore) 7.12 86.1 148.67 3922.84

Better lower lower higher lower

Table 4: FPGA Results.

ns Mbit/s mW

Type Slices LUTs Period Tput Power

Rebel 202 352 3.29 3238.21 1022

AES 2208 3471 5.50 2312.97 1136

Better lower lower lower higher lower

J/bit LUT ∗us Mbit/LUT/s nJ ∗ LUT

Type Energy/Bit LUT*Time Tput/LUT PLT

Rebel 315.63 1159.49 9.2 1185.09

AES 491.29 19208.51 0.67 21827.21

Better lower lower higher lower

We compare REBEL with the AES-128 IP from

OpenCores (OpenCores, ). Tables 2 shows that when

REBEL uses SRAM as key storage, the area de-

creases and the throughput increases. Compared with

AES, REBEL is more compact. REBEL consumes

lower power and chip area and has higher throughput.

As hardware implementation is a multi-dimensional

design which considers power,area and frequency, we

derived the measurements in Table 2 into four data

which are commonly used in cryptography hardware

comparison. The derived data are energy consumed

per bit, area time product, throughput per area and

triple product of power/area/time(PAT). These data

can show the efﬁciency of the cryptography imple-

mentation. The data is shown in Table 3. We can see

that REBEL has lower PAT, AT, energy/bit and higher

throughput/area compared with AES.

The FPGA implementation result (Table 4) agrees

with the ASIC implementation. REBEL occu-

REBEL - Reconfigurable Block Encryption Logic

317

Table 5: FPGA Throughput/Area Comparison.

Type LUTs Gbps Gbps/LUT

REBEL 352 3.24 9.2

AES(Opencore) 3417 2.31 0.68

AES (Chodowiec, 2001) 2507 0.41 0.17

AES (Hodjat, 2004) 9446 21.64 2.29

AES (Zambreno, 2004) 16938 23.57 1.39

AES (Zhang, 2004) 11022 21.56 1.96

pies lesser slices and LUTs compared with AES.

REBEL has higher frequency, throughput and lower

power consumption compared with AES. In addition

REBEL has higher Throughtput per LUT compared

with other AES implementations (Feldhofer et al.,

2005) as shown in Table 5.

6 CONCLUSIONS

Two of the desirable characteristics of a symmetric

block cipher are larger key size to avoid key collision

attacks, and high throughputs. We have presented a

new block encryption algorithm - REBEL, with these

two attributes. It is able to support signiﬁcantly larger

key space for the same block size (576 key bits for

32-bit block size for instance). Moreover, the in-

creased key space can be supported with the through-

puts slightly higher than that of AES-128 both in soft-

ware and hardware implementations.

The REBEL function uses the gate truth-tables as

the secret keys directly. These gates naturally have

the desirable attribute of nonlinearity. Linear crypt-

analysis is less likely to succeed due to this. We use

the square of a Boolean function as the underlying 1-

way function within an LR-network. This takes away

differential controllability and observability making

differential cryptanalysis impractical. This also lends

some provable security to the REBEL construction.

REFERENCES

(1970-). GOST 28147-89. Wikipedia Article.

(1997). TREYFER. Wikipedia Article.

Anderson, R. J., Biham, E., and Knudsen, L. R. (2000). The

case for serpent. In AES Candidate Conference, pages

349–354.

Biham, E., Biryukov, A., and Shamir, A. (2005). Cryptanal-

ysis of Skipjack Reduced to 31 Rounds Using Impos-

sible Differentials. J. Cryptology, 18(4):291–311.

Biham, E. and Shamir, A. (1991). Differential Cryptanaly-

sis of DES-like Cryptosystems. J. Cryptology, 4(1):3–

72.

Biryukov, A. and Wagner, D. (1999). Slide attacks. In Fast

Software Encryption, pages 245–259.

Chodowiec, P., Khuon, P., and Gaj, K. (2001). Fast im-

plementations of secret-key block ciphers using mixed

inner- and outer-round pipelining. In FPGA ’01: Pro-

ceedings of the 2001 ACM/SIGDA ninth international

symposium on Field programmable gate arrays, pages

94–102, New York, NY, USA. ACM.

eStream. The estream project.

http://www.ecrypt.eu.org/stream/.

eStream. Performance comparison of vari-

ous stream ciphers by estream project.

http://www.ecrypt.eu.org/stream/phase3perf/2007a/

pentium-4-a/.

Feldhofer, M., Lemke, K., Oswald, E., Standaert, F.-X.,

Wollinger, T., and Wolkerstorfer, J. (2005). State

of the art in hardware architectures. Technical Re-

port D.VAM.2, ECRYPT, European Network of Ex-

cellence in Cryptology.

Hodjat, A. and Verbauwhede, I. (2004). A 21.54

gbits/s fully pipelined aes processor on fpga. Field-

Programmable Custom Computing Machines, 2004.

FCCM 2004. 12th Annual IEEE Symposium on, pages

308–309.

Kutz, M. (2004). The complexity of boolean matrix root

computation. Theor. Comput. Sci., 325(3):373–390.

L’Ecuyer, P. and Simard, R. J. (2007). Testu01: A c li-

brary for empirical testing of random number genera-

tors. ACM Trans. Math. Softw., 33(4).

Lie, D., Thekkath, C. A., Mitchell, M., Lincoln, P., Boneh,

D., Mitchell, J. C., and Horowitz, M. (2000). Ar-

chitectural support for copy and tamper resistant soft-

ware. In Architectural Support for Programming Lan-

guages and Operating Systems, pages 168–177.

Matsui, M. (1993). Linear Cryptoanalysis Method for DES

Cipher. In EUROCRYPT, pages 386–397.

Miyaguchi, S. (1990). The FEAL Cipher Family. In

CRYPTO, pages 627–638.

National Bureau of Standards (1999). FIPS PUB 46-3: Data

Encryption Standard (DES). Federal Information Pro-

cessing Standard.

National Bureau of Standards (2001). FIPS PUB 197: Ad-

vanced Encryption Standard (AES). Federal Informa-

tion Processing Standard.

OpenCores. Opencores project. http://www.opencores.org.

Suh, G., Clarke, D., Gassend, B., van Dijk, M., and De-

vadas, S. (2003). aegis: Architecture for tamper-

evident and tamper-resistant processing. In Proceed-

ings of the 17 Int’l Conference on Supercomputing,

pages 160–171.

Wagner, D. (1999). The boomerang attack. In Fast Software

Encryption, pages 156–170.

Zambreno, J., Nguyen, D., and Choudhary, A. N. (2004).

Exploring area/delay tradeoffs in an aes fpga imple-

mentation. In FPL, pages 575–585.

Zhang, X. and Parhi, K. K. (2004). High-speed vlsi archi-

tectures for the aes algorithm. IEEE Trans. Very Large

Scale Integr. Syst., 12(9):957–967.

SECRYPT 2008 - International Conference on Security and Cryptography

318