MULTI-COLLISIONS ATTACK IN RING HASH STRUCTURE

Nasour Bagheri

, Babak Sadeghiyan

Electrical Engineering Department, Iran University of Science and Technology (IUST)

Computer Engineering Department, Amirkabir University of Technology Tehran, Iran

Majid Naderi

Electrical Engineering Department, Iran University of Science and Technology (IUST), Iran

Keywords: Ring Hash Structure, Single Feedback Ring Hash, Multi Feedback Ring Hash, Hash function, Multi-

collision Attack, Joux Attack, Preimage Attack, r-way collision.

Abstract: Ring hash structure is a new hash structure which has been introduced by Joux to strengthen the current

hash structures against multi-collision attacks. In this paper, we present a cryptanalysis on Ring hash

structure. We show that finding multi-collisions, i.e. 2

-way collision, for a Ring hash structure is not much

harder than finding such multi-collisions for ordinary MD hash structure. The complexity of our attack is

approximately

(

)

log n times harder than the complexity of attacks against MD structures. We employ these

multi-collisions to find a D-way pre-image for this structure. We show the complexity of finding 2

-way

multi-collision and 2

-way preimage are

()()

(

)

1/22

Ok n+× ×

and

(

)

/2 2 2 2

Ok n××+×

respectively. We

also show that Ring structure should not be used to create a hash function of 2n-bit length, by concatenating

this structure to any other hash structure of n-bit output length. We show that the time complexity of finding

a collision for this concatenated structure is

()()

(

)

1/22

Ok n+× ×

that is much smaller than

(

)

Ω ,

which is expected for a generic-birthday attack.

1 INTRODUCTION

Hash functions are used widely as a cryptographic

primitive for generating digital signatures and

message authentication codes. Each cryptographic

hash functions should satisfy some security criteria.

The main security requirement for a hash function is

its collision freeness. Informally, it means that no

attacker should be able to find a pair of different

messages M and M’ leading to equal hash values.

Moreover, hash functions with output block length

smaller than 160 bits are nowadays considered as

insecure, due to general birthday attack.

In practice, building a cryptographic function

with an input of variable size is not a simple task.

Most hash functions are based on an iterated

construction that makes use of a compression

function, whose inputs have fixed sizes. A well-

known family of such a construction are MDx hash

function family, including MD4 (Rivest, 1992),

MD5 (Rivest, 1995), and SHA (FIPS 180–1, 1995).

The principle behind this structure is that if there is

a computationally collision-free function

from m

bits to n bits, where n < m (Damgard, 1990) then

there is a collision-free hash function h mapping a

message of arbitrary polynomial length to a k-bit

string. Due to Merkle-Damg°ard theorem, it is

claimed that if IV is fixed and if the padding

procedure includes the length of the input into the

padding bits, then h is collision-resistant if

collision-resistant (Damgard, 1990, Merkle, 1990).

Hence, it has been generally thought that the

problem of designing a collision-resistant hash

function has been reduced to the problem of

designing a collision-resistant compression

function. However, the multi-collision attack (Joux,

2004) and the multi-block differential collision

attack on MD5, SHA-0 and SHA-1 (Biham, 2005,

Wang, Yin, 2005, Wang, Yu, 2005) indicates that a

collision-resistant compression function is not a

sufficient condition of a collision- resistant hash

function, but only a necessary condition. It means

that a secure and collision- resistant hash function

will be based not only on a collision-resistant

compression function, but also on a collision-

resistant structure.

278

Bagheri N., Sadeghiyan B. and Naderi M. (2008).

MULTI-COLLISIONS ATTACK IN RING HASH STRUCTURE.

In Proceedings of the International Conference on Security and Cryptography, pages 278-284

DOI: 10.5220/0001917102780284

 SciTePress

Attacks to Hash function can divide in two

groups. First group, e.g. Wang Attack (Wang, Yin,

2005, Wang, Yu, 200), includes attacks that use

weaknesses of compression function. Second group

of attacks, e.g. Joux (Joux, 2004) attack, includes

attacks that use weaknesses of iterative structures,

which are generic attacks to iterative structures such

as MD structure. Actually, in this attack, increasing

the security of compression function does not lead to

strengthen the structure against multi-collision

attack. This attack was shown that there is a

-way

collision attack for the classical iterated hash

function based on a compression

function,

{} {}

:0,1 0,1

mn n

→

where the time

complexity of the attack is

(

)

Ok×

. This

complexity is much less than the complexity for the

generalized birthday attacks which is

()

n −

⎛⎞

⎜⎟

⎝⎠

. This

is the basic idea of Joux’s attack. The main strategy

of Joux’s attack is to the first find k successive

collisions by performing k successive birthday

attacks. The attack works as follows:

– Let

h be equal to the initial value IV of H.

– For i from 1 to k do:

• Call C and find

and

′

such that

(

)

(

)

ii ii i i

h M f h M and M M

−−

′′

=≠

• Let

()

iii

hfhM

−

– Pad and output the

messages of the form

(

)

, ,..., ,

m m m Padding

(where

m is one of the two

blocks

′

Clearly, the 2

different messages built as above,

all reach the same final value. A schematic

representation of these 2

messages together with

their common intermediate hash values is drawn in

Figure 1.

After introducing this attack, many structure

have been proposed to strength iterated structure

against this type of attach such Ring hash (Su, 2006)

3C and 3C+ (Gauravaram, 2006), Zipper hash

(Liskov, 2006), WPH and DPH (Lucks, 2005), L-

pipe(Speirs, 2007), etc. All this structure tries to

strength against multi-collision or multi-block

attack. Among this new hash structure, in our

investigation, we analysis strengthen of Ring hash

(Su, 2006) against multi-collision attack.

This paper is organized as following. Section 2

is a brief description of Ring hash function. Section

3 describes our attack for finding multi-collision for

this structure. In section 4, we present a preimage

attack for this structure. Section 5 present the

security of 2n-bit Ring based hash function.

Conclusions will be presented in section 6.

2 RING HASH STRUCTURE

There is two different variant of ring hash structure,

called Single-feedback ring hash (SFRH) and multi-

feedback ring hash (MFRH). The Ring hash

structure can be considered as a general hash

function construction. To build an n-bit hash

function, it needs a compression functions

and

an IV as initial chaining value. The function

can

be seen as

{} {}

0,1 0,1

nm n+

→ mapping with nm

≤

where m is single message block length and n is

hash value out put length. Surprisingly, for his

structure if original message length is division of

padding will be neglected (Su, 2006) , but if we

consider a standard way of padding, it will not

affect proposed attack. In standard padding

schemas with function P(x), for input x it is

guaranteed to return a padded value such that P(x)

is a string that can be broken down into m-bit length

blocks, and for all

()

(

)

',' '

MM PM MPM≠≠

SFRH works as follow:

1. Let

,...,

M be m-bit strings such

that

(

)

,...,

MMPM= .

2. Fix

hIV=

,...,

hh are computed iteratively as

(

)

iii

hfMh

−

= .

4. Set the

112

lll

MM M

= , and

the

(

)

lll

hfM h

=↔ .

5. The message digest is

(

)

(

)

221

lll

HM h fM h

+++

== .

where sign

↔

denotes reversal operation, that is,

the bits of a variable are arranged in reverse order.

For example the reverse code of ‘100110’ is

‘011001’. In Figure 2, SFRH hash construction has

been illustrated.

MFRH works as follow:

1. Let

,...,

M be m-bit strings such

that

(

)

,...,

MMPM= .

2. Let

,...,

M be m-bit strings such

that

(

)

,...,

MMPM= .

MULTI-COLLISIONS ATTACK IN RING HASH STRUCTURE

279

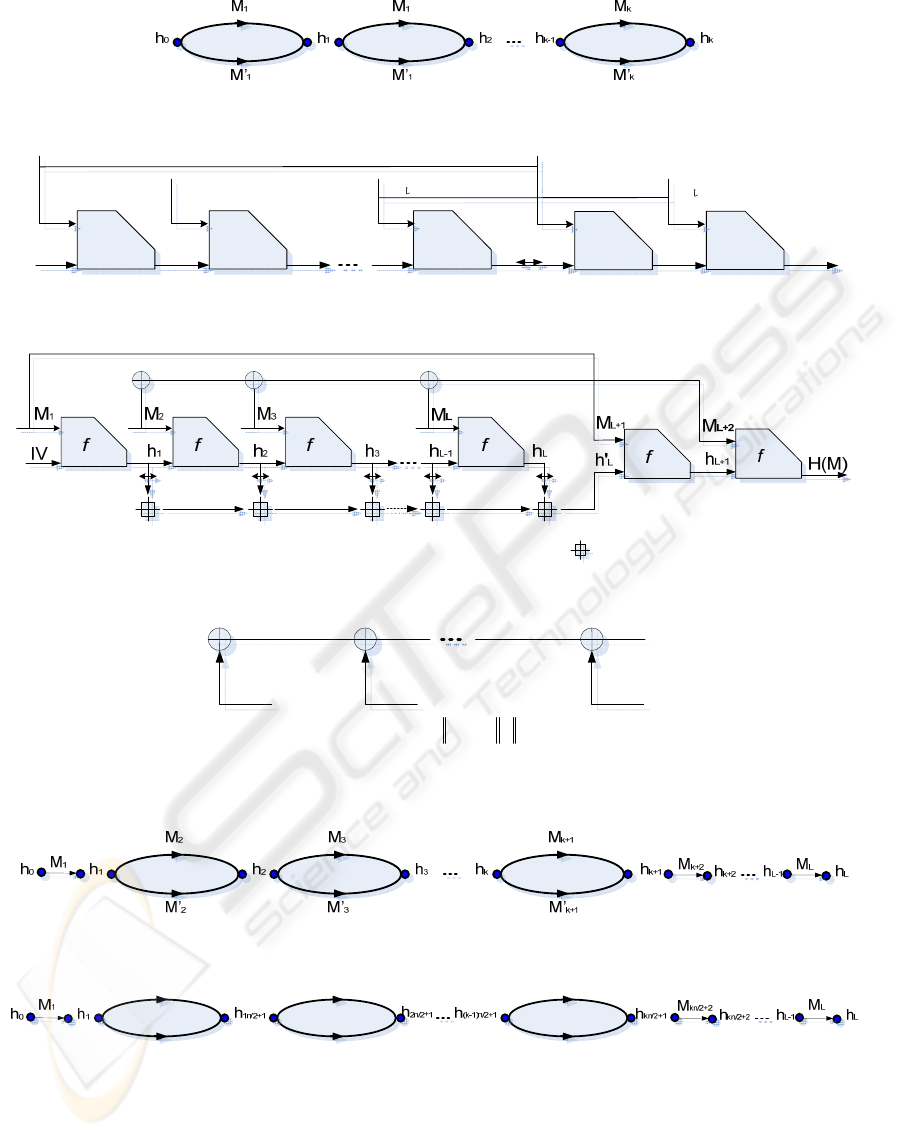
Figure 1: Schematic representation of Joux multi-collision construction.

1 M2

H(M)

h1 h2 hL-1 hL

h'L

hL+1

Figure 2: The Single Feedback Ring Hash (SFRH) structure, sign

↔

denotes reversal operation.

Figure 3: The Multi Feedback Ring Hash (MFRH) structure, sign

↔

⊕

, and denote reversal operation, binary XOR

and modular addition respectively.

(

)

()

2/1 nj

()

2/122/12/

...

njjnjnj

mmm

+++

=Ψ

Figure 4: The

(

)

function structure.

Figure 5: Schematic representation of multi-collision attack on SFRH.

′

Figure 6: Schematic representation of multi-collision attack on SFRH.

SECRYPT 2008 - International Conference on Security and Cryptography

280

3. Let

,...,

be m-bit strings such

that

(

)

,...,

MMPM= .

4. Fix

hIV= .

hh ,...,

are computed iteratively as

()

−

iii

hMfh

6. Set

112

lli

MM M

⊕

()

′

=↔

∑

and

()

lll

hfMh

′

7. Set

112

lli

MM M

⊕

()

′

=↔

∑

and

()

lll

hfMh

′

8. The message digest

() ( )

221

lll

HM h fM h

+++

== .

Where, notations

↔ ,

⊕

, and are denote

reversal operation, binary XOR and modular

addition respectively. Figure 2 illustrated MFRH

hash construction.

3 MULTI-COLLISION ATTACK

ON RING HASH

Ring hash structure has developed as a structure that

could strength multi-collision attack. In this section,

we show that constructing multi-collisions in Ring

hash function can be done in an efficient way. If we

consider collisions between messages of the same

length, in this case the blocks of padding are

identical and the padding process can be ignored.

Moreover, if the intermediate hash chaining values

collide at some point in the hash computation of

two messages, the following values remain equal as

while as the reminder of the messages are identical.

Thus, on messages of the same length, collisions

without the padding clearly lead to collisions with

the padding.

Although this attack could be apply for any

length of message block and chaining value, but for

simplicity of prove, we assume that the size of the

message blocks is bigger than the size of the

chaining values. However, the attack can be easily

generalized to the other case. We also assume that

we can access two collision finding machines

C and 'C . C is a machine that given as input a

chaining value

h outputs two different blocks

and

such that

()( )

,,'

hM f hM= . This collision

finding machine may use the generic birthday attack

or any specific attack based on a weakness of

The most relevant property is that

C should work

properly for all chaining values. It’s clear that most

of these assumed conditions for our scenario are

similar to what considered in (Joux, 2004), for

generating multi-collision attack on ordinary MD.

On the other hand,

'C is a collision finding

machine that given

different single block

message pairs

m and

′

and finds to multi-blocks

and '

so that

() ( )

'FFΨ= Ψ where

()

Ψ=

⊕

is ordinary XOR of all /2n blocks of

multi-block

where illustrated in Figure 4. 'C is a

machine that can find collision with solving

following equations:

0 0,0 0 0,0 1 1,0

1 1,0 ,0 ,0

00,0 0,011,0

1 1,0 ,0 ,0

0 0,1 0 0,1 1 1,1

1 1,1 ,1 ,1

00,1 0,111,1

...

kkkk

kk kk

aM aM aM

aM a M aM

bM bM bM

bM b M bM

aM a M aM

a M aM aM

bM bM bM

′′

×⊕×⊕×⊕

′

′′ ′′

×⊕⊕× ⊕×

′′

×⊕×⊕×⊕

′′ ′′

×⊕⊕×⊕×

′′

×⊕× ⊕×⊕

′

′′ ′′

×⊕⊕×⊕×

′′

×⊕×⊕×⊕

′

1 1,1 ,1 ,1

00, 00, 11,

11, , ,

00, 00, 11,

11, , ,

...

kk kk

nnn

nkknkkn

nnn

nkknkkn

bM bM bM

aM a M aM

a M aM aM

bM b M bM

bM b M b M

⎧

⎪

⎨

⎪

′′′

×⊕⊕×⊕×

⎪

⎪′′

×⊕× ⊕×⊕

⎪

′

′′ ′′

×⊕⊕×⊕×

⎪

′′

×⊕× ⊕×⊕

⎪

′′ ′′

×⊕⊕× ⊕×

⎪

⎩

00 11

1, 1 , ... , 1

aa aa aa

bb bb bb

′′ ′

⊕=⊕ =⊕

⎧

⎪

⎨

⎪

′′ ′

=⊕ =⊕ =⊕

⎩

(1)

Here,

,ij

is the j

bit of the i

message block.

But, how many messages do we need to solve this

equation with non negligible probability? Actually,

this linear equation would find some value

for

,,,, 0

iiii

aaba for i k

′

≤

≤ . If adversary wants to

insure that there is any solution for these equations,

he must increase the number of messages pair. If he

selects two distinct messages, the probability that

they satisfy the condition is equal to

n−

2 . If he

wants to find any solution for given linear

equations, he need to determine k in such a way:

MULTI-COLLISIONS ATTACK IN RING HASH STRUCTURE

281

1/2

⎛⎞

⎜⎟

⎝⎠

≥

(2)

Therefore, if he selects

/2kn= , this probability

will be equal to

1/ 2 . Because of the second part of

the equation, he can reduce the number of variables

from

2 nton× variables, so the time complexity of

solving this linear equation is

()

On .

3.1 Multi-Collision Attack on SFRH

In this section, we prove that constructing 2

collisions on SFRH approximately cost

k times as

much as building multi-collisions in the ordinary

MD structure. In particular, we claim that we can

generate

equal collision on SFRH by only

(

)

calls to the C oracle machine which is much less

than what we expected from birthday

paradox

()

(

)

/2 /2

212

×−

⎛⎞

⎜⎟

⎝⎠

. Assume that l , number of

message blocks, satisfies

2lk≥+. The attack works

as follows:

1. Let

h be equal to the initial value IV of

Ring Hash.

2. Set

()

101

,hfhM=

3. For i from 2 to

1k + do:

a. Call

C and find

and

′

in such a way

that

()()

ii ii

hM fhM

−−

′

b. Set

()

iii

hfhM

−

= .

4. Output the

2 messages of form

()

12 1

, ,..., , ,...,

kk l

mmM M

where

m is on of the two

multi blocks

and '

Obviously, since

have been fixed

and

21ik≤≤ +→

()()

ii ii

hM fhM

−−

′

, for all 2

different messages

′

, and

are equal

and

different messages generated in this way are

result the same value of hash.

Time complexity of attack is equal to all attempt

that adversary do. It is equal to

k × for finding

2-way collision. Figure 5 is a schematic illustration

of these

multi-blocks messages together with

their common intermediate hash values.

3.2 Multi-Collision Attack on MFRH

In this section we show that how the adversary can

generate

equal collision by only

()

/2Ok n×

calls to the C oracle and

()

Ok calls to C

′

oracle

machine, which is much less than what we expected

from birthday paradox

()

(

)

/2 2 1 2

×−

⎛⎞

⎜⎟

⎝⎠

. Assume

that

, number of message blocks,

satisfies

22lkn≥× +. The attack works as follows:

1. Let

h be equal to the initial value IV of

Ring Hash.

2. Set

(

)

101

,hfhM=

3. For i from 2 to

21kn×+ do:

a. Call

C and find

and

′

in such a way

that

(

)

(

)

ii ii

hM fhM

−−

′

= .

b. Set

(

)

iii

hfhM

−

4. For j from 1 to k do:

a. Give the

/2n different single block message

pairs of

(

)

MM through

()

/2 1

1/22

×+

−+

'C machine to find

and '

Ψ so

that

(

)

(

)

′

=Ψ.

5. Output the

messages of form

(

)

11 /22

, ,..., , ,...,

kkn l

ψψ

×+

where

is on of the

two multi blocks

and '

Obviously, since

have been fixed and

for

21ik

≤

≤+→

(

)( )

ii ii

hM fhM

−−

′

, for all

these

different messages

and

are equal

and all the

different messages generated in this

way are result the same value of hash.

Third step of this algorithm finds

()

kn×

different multi-collision for forward part of MFRH

which uses

as compress function and fourth step

find

different multi-collision for feed-forward

part of MFRH hash which produces

⊕

. Time

complexity of attack is equal to all attempt that

adversary doing. It is equal to

()

kn×× for

finding 2-way collision in forward path of attack

and

()

/2kn× for finding 2-way collision in feed-

forward path, related to time complexity of

′

machine. Figure 6 is a schematic illustration of

SECRYPT 2008 - International Conference on Security and Cryptography

282

these

multi-blocks messages together with their

common intermediate hash values.

4 FINDING K-WAY

SECOND-PREIMAGE ATTACK

ON RING HASH

In reference (Joux, 2004) Joux puts forward an attack

method called k-way second-preimage which is

applicable for finding the second preimage of an

output of a hash function based on the MD

structure. For a given hash target

value

(){}

0,1 ,

YHM=∈ the attackers first find

collisions on r-block messages

, ,...,

where

() ()

()

...

HHM HM HM==== . Then, he

finds the block

such that

(

)

HM Y

. In

this way, the attackers succeed in finding

second

preimages to the message M. Obviously, the time

complexity of this attack is

(

)

Or +

4.1 Finding k-Way Second-Preimage

Attack on SFRH

For a hash function based on the SFRH structure,

we show that adversary can find

-way preimage

and second preimage in cost of

(

)

Or + . The

attack works as follows:

1. Fixed

with some random value.

2. Set

(

)

,hfIVM=

3. For i from 2 to

1r +

do:

a. Call

C and find

and

′

so that

(

)

(

)

ii ii

hM fhM

−−

′

b. Set

(

)

iii

hfhM

−

4. Find

in such a way

()

(

)

(

)

121 2

,,,

rr r

ffhMMM Y

++ +

↔=.

5. Output the

messages of form

(

)

12 1

, ,..., ,

Mm mM

where

m is on of the two multi

blocks

and '

Obviously, all

different messages generated

in this way are led to value

Y as hash result. This

procedure can divide in two parts. Fist part of attack

is finding

-way collision which cost

r × and

second part which contain in step 4, related to

finding a preimage to guaranteed the successes of

attack which cost

. Therefore, all time complexity

of the attack is equal to what has been clamed.

By Appling a similar procedure, adversary can

find

-way second preimage with identical cost of

time complexity which is far from ideal value,

which is

(

)

Ω×

4.2 Finding k-way Second-Preimage

Attack on SFRH

For a hash function based on the SFRH structure,

we show that adversary can find

-way preimage

and second preimage in cost of

()

/2 2 2

Or n×+.

The attack works as follows:

1. Fixed

with some random value.

2. Set

(

)

,hfIVM=

3. For i from 2 to

1r +

do:

a. Call

C and find

and

′

in such a

way

(

)

(

)

ii ii

hM fhM

−−

′

= .

b. Set

(

)

iii

hfhM

−

= .

4. for j from 1 to r do:

a. Call

'C to find

and '

Ψ among

different messages of

2n blocks length in such a

way that

(

)

(

)

′

Ψ= Ψ.

5. Find

/2 2rn

so that

()

12 1

,,,

rr i

ffhM hMMiY

⎧⎫

⎡⎤

⎛⎞

⎪⎪

↔

+↔ =

⎨⎬

⎢⎥

⎜⎟

⎝⎠

⎪⎪

⎣⎦

⎩⎭

∑

⊕

6. Output the

messages of

form

(

)

11 1 2

, ,..., ,

ψψ

where

is on of the two

multi blocks

and '

Obviously, all

different messages generated

in this way are led to the value

Y , as hash result.

This procedure can divide in two parts. The first

part of the attack, steps 3 and 4, is finding

-way

collision in MFRH which cost

()

/2 2

Or n×× and

second part which contain in step 5, related to

finding a preimage to guaranteed the successes of

attack which cost

(

)

O . Therefore, all time

complexity of attack is equal what has been clamed.

By Appling a similar procedure, adversary can

find

-way second preimage with identical cost of

time complexity which is far from ideal value,

which is

(

)

Ω× .

MULTI-COLLISIONS ATTACK IN RING HASH STRUCTURE

283

5 RING HASH IN 2N-BITE

CONCATENATED STRUCTURE

A natural construction to build large hash values is

to concatenate several smaller hashes. For example,

given two hash functions F and G, it seems

reasonable given a message M to form the large

hash value

()()

()

FM GM . In this construction, F

and G can either be two completely different hash

functions or two slightly different instances of the

same hash function. In (

Joux, 2004) Joux has shown

that if at least one of these hash function be a MD

iterated hash function, complexity of finding a

collision for this structure is slightly more than

finding collision for one branch and equal to

()

/2 2

On × .

The basic idea in this attack is finding

-way

collision for MD structure and find a collision

among this

different message for the second

hash function. Clearly this collision is applicable to

booth branches. Whit similar task, adversary could

seek a collision for Ring hash structure. These

attacks are difference in the first part complexity

and complexity of the first par for SFRH and

MFRH are

()

(

)

/2 2

On ×

and

()( )

(

)

/2 /2 1 2

On n×+×

respectively.

6 CONCLUSIONS

In this paper, we showed that finding multi-

collisions in Ring hash structure are not much

harder to find than finding multi-collisions in MD

hash structure. Actually, we proved that finding

multi-collisions in SFRH is as difficult as finding it

on ordinary MD, and for MFRH, it is a little harder

than what for MD is. Also, we have shown that

finding

-way preimages and second preimages on

these structures are not really harder to find than

ordinary preimages and second preimages.

Moreover, we shown that ring hash structures can

not be used as a building block for creating 2n-bite

concatenated hash structure because of its strength

against collision attack, which is much less than

ideal one. Our study have shown that although this

structure is slightly more secure than MD iterated

hash structure, but is really far from perfect hash

function.

REFERENCES

Biham, E., Chen, R, and Joux, A., etc, 2005. Collisions of

SHA-0 and Reduced SHA-1, Advances in

Cryptology-EUROCRYPT’05, pp.36–57, Springer-

Verlag.

Damgard, I., 1990. A design principle for hash functions,

in Advances in Cryptology – Crypto’89 (G. Brassard,

ed.), no. 435 in Lecture Notes in Computer Science,

pp. 416–427, Springer-Verlag.

FIPS, 180–1, 1995. Secure hash standard. FIPS

publication.

Gauravaram, P., Millan, W., Dawson, E. and

Viswanathan, K., 2006. Constructing Secure Hash

Functions by Enhancing Merkle-Damgard

Construction., Information Security and Privacy,

(Batten, L., Safavi-Naini, R., ed.) volume 4058 of

Lecture Notes in Computer Science, pp. 407–420,

Springer.

Joux, A., 2004. Multi-collisions in Iterated Hash

Functions. Application to Cascaded Constructions

Advances in Cryptology-CRYPTO’04, pp. 306–316,

Springer-Verlag.

Lucks,S. , 2005. A failure-friendly design principle for

hash functions. In Bimal Roy, editor, Advances in

Cryptology-ASIACRYPT’05, volume 3788 of Lecture

Notes in Computer Science, pp. 474-494, Springer-

Verlag.

Merkle, R., C., 1990. One-way hash functions and DES in

Advances in Cryptology – Crypto’89 (G. Brassard,

ed.), no. 435 in Lecture Notes in Computer Science,

pp. 428–446, Springer-Verlag.

Rivest, R., L., 1992. The MD4 Message – Digest

Algorithm. Network MIT laboratory for Computer

Science and RSA Data Security , Inc RFC 1320.

Rivest, R., L., 1992. The MD5 message-digest algorithm,

Request for Comments (RFC1320), Internet Activities

Board, Internet Privacy Task Force.

Speirs, W., R. and Molly, J., 2007. Making large Hash

Functions from small compression function.

available:http://eprint.iacr.org/2007/239.ps.

Su, S., Yang, Y., Yang, B. and Zhang, S., 2006. The

Design and Analysis of a Hash Ring-iterative

Structure, available: http://eprint.iacr.org/2006/384.pdf

Wang, X., Yin, Y., L., and Yu, H., 2005. Finding

collisions in the full SHA-1, Advances in Cryptology-

CRYPTO’05, pp. 17–36, Springer-Verlag.

Wang, X. and Yu, H., 2005. How to Break MD5 and

Other Hash Functions, Advances in Cryptology -

EUROCRYPT’05, pp. 19–35, Springer-Verlag.

SECRYPT 2008 - International Conference on Security and Cryptography

284