SCHEMA MAPPING FOR RDBMS
Calin-Adrian Comes, Ioan Ovidiu Spatacean, Daniel Stefan, Beatrice Stefan
Petru Maior University, Department of Financial&Accounting
Nicolae Iorga 1, 540088 Tg-Mures, Romania
Lucian-Dorel Savu
Dimitrie Cantemir University, Department of Financial&Accounting
Bodoni Sandor 3-5, 540055 Tg-Mures, Romania
Vasile Paul Bresfelean, Nicolae Ghisoiu
Babes-Bolyai University, Department of IT Applied to Economics
Teodor Mihali 58-60, 400691, Cluj-Napoca, Romania
Keywords:
Schema mapping, Stored procedures, Triggers.
Abstract:
Schema mapping is a specification that describes how data structured from one schema S the source schema is
to be transformed into data structured under schema T, the target schema. Schemata S and T without triggers
and/or stored procedures(functions and procedures) are statical. In this article, we propose a Schema Mapping
Model specification that describes the conversion of a Schema Model from one Platform-Specific Model to
other Platform-Specific Model according to Meta-Object Facility-Query/Verify/Transform in dynamical mode.
1 INTRODUCTION
Applications as database warehousing, global infor-
mation systems and eletronic commerce need to take
the existing schema with particular source S and use
it in diferent form, but they need to start with under-
standing how will be the target schema T. Data ex-
change are used in many tasks in theoretical stud-
ies research and practical in software products. In
early stage 1977, in (Shu et al., 1977) with their EX-
PRESS, data exchange system with main functional-
ity conversion data between hierarchical schemata the
data exchange was in the top research topics. In (Fa-
gin et al., 2003) Ronald Fagin et al. underline that
the data exchange problem meet the foundation and
algorithmic issues; their theoretical work has been
motivated by the development of Clio (Miller et al.,
2000; Popa et al., 2002), a prototype for data ex-
change and schema mapping from source schema S
to target schema T, the precursor of changes in SQL
Assist from IBM DB2 family.
2 RELATED WORK
According to (Fagin et al., 2003) we have
the source schema S =hS
1
, S
2
, . . . , S
n
i, where
S
i
’s are the source relation symbols, the tar-
get schema T =hT
1
, T
2
, . . . , T
m
i, where T
i
’s are
the target relation symbols and the schema
hS, Ti = hS
1
, S
2
, . . . , S
n
, T
1
, T
2
, . . . , T
m
i. All in-
stances over the S represent source instances I,
while instances over T J are target instances. If I
is a named source instance in S and J is a named
target instance the K = hI , J i is the named instance
over the schema hS, Ti. A dependency named
source-to-target dependencies over hS, Ti of the form
(∀x)(φ
S
(x) → χ
T
(x))
where φ
S
(x) is an expression(formula), with free vari-
able x = (x
1
, x
2
, . . . , x
k
) of logical formalism over S
and χ
T
(x) is an expression(formula) with free vari-
able x = (x
1
, x
2
, . . . , x
l
) of logical formalism over T. A
dependency named target dependencies over the tar-
get schema T (the target dependencies are different
from those use for the source-to-target dependencies)
541
Comes C., Ovidiu Spatacean I., Stefan D., Stefan B., Savu L., Paul Bresfelean V. and Ghisoiu N. (2008).
SCHEMA MAPPING FOR RDBMS.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - DISI, pages 541-544
DOI: 10.5220/0001727505410544
Copyright
c
 SciTePress

CREATE TRIGGER NEWHIRED
AFTER INSERT ON EMPLOYEE
BEGIN
UPDATE DEPT
SET EmpN = EmpN +1
WHERE
EmployeeID=:New.EmployeeID
END;
CREATE TRIGGER "NEWHIRED"
AFTER INSERT OF EmployeeID
ON EMPLOYEE
REFERENCING OLD AS EO
NEW AS EN
FOR EACH ROW
BEGIN
UPDATE DEPT
SET DEPT.EmpN=DEPT.EmpN +1
WHERE
EMPLOYEE.EmployeeID=EN
END;
TRANSLATOR
SOURCE
TARGET
ERROR
MESSAGES
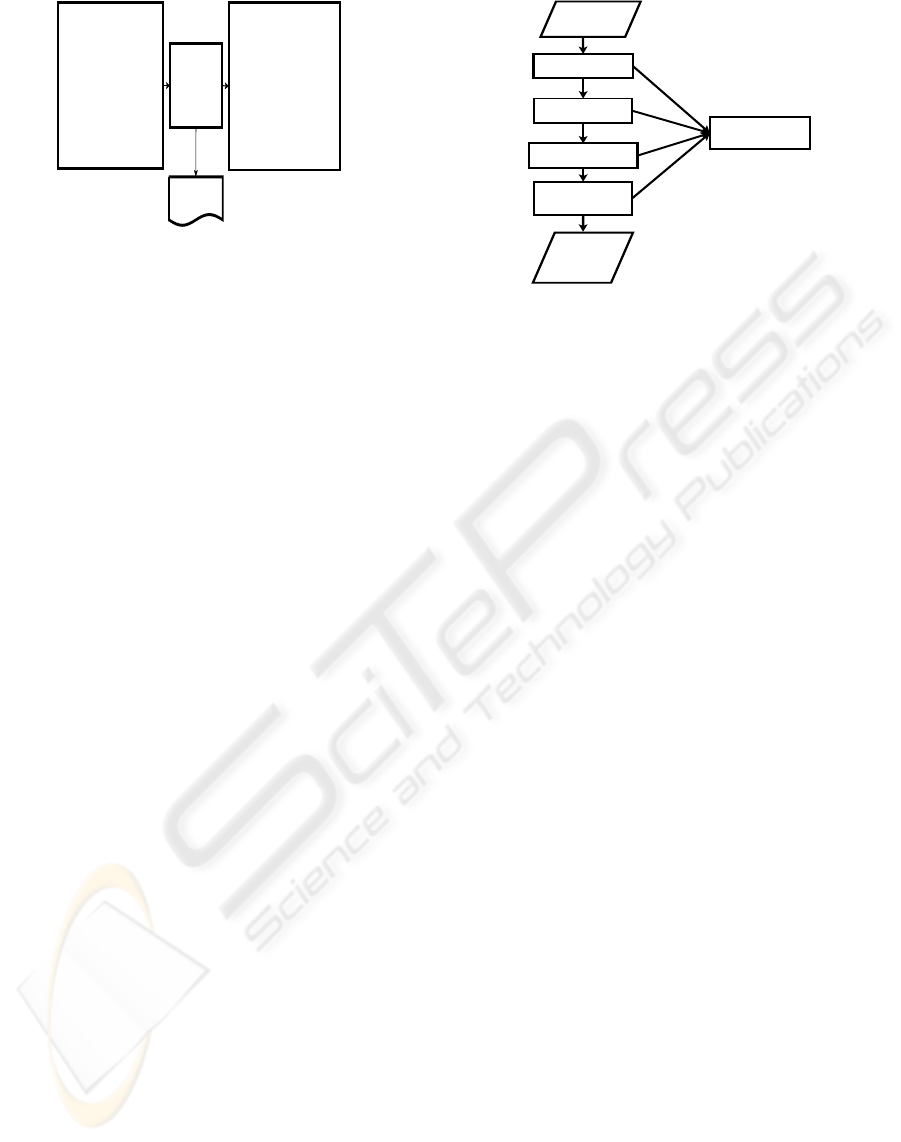
Figure 1: A translator.
Definition 2.1. A data exchange represent a 4-tuple
DE = (S, T,
∑
st
,
∑
t
) with a source schema S, a target
schema T, a set
∑
st
of source-to-target dependencies
and set
∑
t
of target dependencies.
In (Berri and Vardi, 1984) Berri et al., proved that for
practical purposes eachsource-to-target dependency
∑
st
represents a tuple-generating-dependency(tgd) of
the form
(∀x)(φ
S
(x) → χ
T
(x,y))
where φ
S(x)
represents a conjunction of atomic ex-
pression(formulas) over S and χ
T
(x,y) represents a
conjunction of atomic expression(formulas) over T.In
(Fagin et al., 2005b) Fagin et al. identified a particu-
lar universal solution for data exchange and schema
mappings, and argued that this is the best universal
solution.
Definition 2.2. A translator represents a program
that reads on input in one language the source lan-
guage - source code program - and translate it into
output in an equivalent program in other language the
target language - source code - see Figure 1
A translator operates in the following phases: lex-
ical analyzer, syntax analyzer, semantic analyzer, tar-
get code generator. In early stage 1950’s Naom
Chomsky (Chomsky, 1956) proposed the formal
definition for context-free grammar, see Figure 2.
Context-free are used in the design and description of
programming languages, compilers and translators.
A context-free grammar is 4-tuple:
G = (V,
∑
, R, S)
where V - represents a finite set of non-terminal char-
acters or variables;
∑
- represents set of terminals, dis-
joint with V; R - represents a finite set of rules; S -
represents the start variable, used to represent the or
program.
Definition 2.3. Let
∑
1
and
∑
2
be two alphabets,
named source alphabet respective target alphabet and
two languages L
1
⊂
∑
∗
1
, L
2
⊂
∑
∗
2
. A translator from
the language L
1
to the language L
2
is a relation T from
∑
∗
1
to
∑
∗
2
when the domain of T is L
1
and the image
of T is L
2
.
SEMANTIC ANALIZER
SYNTAX ANALIZER
TARGET CODE
GENERATOR
LEXICAL ANALIZER
SOURCE
CODE
TARGET
SOURCE
CODE
ERROR
HANDLER
Figure 2: Phases of a translator.
T :
∑
∗
1
→
∑
∗
2
where dom(T)= L
1
and img(T)=L
2
In (Pranevicius, 2001) Pranevicius H. present an ap-
proach in idea to use Z specification language for de-
velopment aggregate formal specifications, because
the use of Z schemata in aggregate model permits
mathematically strictly define data structures used
in system description.
The formal specification approach using both ag-
gregate approach an Z specification language are use-
ful for specification the dynamichal behaviour of dis-
tributed information system and the large and global
relational database systems.
In (Andreica et al., 2005) Andreica et al. they pro-
posed a model who aims at proving the consistency
of such transformations, which are often used in soft-
ware applications that process databases; a symbolic
model for the transformations between the relational
database form and its XML representation.
3 OUR APPROACH
Our algebrical approach to data exchange and schema
mapping is to include the stored procedures in schema
mappings and to snapshot the dynamical of the
schemata content in time extending (Fagin et al.,
2003; Fagin et al., 2005b; Fagin et al., 2005a; Fa-
gin, 2007; Fagin and Nash, ings), because they
parse the statical schema mapping not a dynami-
cal schema mapping. We propose the source
schema S(t) =hS
1
(t), S
2
(t), . . . , S
n
(t)i, where S
i
(t)’s
are the source relation symbols, the target schema
T(t) =hT
1
(t), T
2
(t), . . . , T
m
(t)i, where T
i
(t)’s are the
target relation symbols and the schema hS(t), T(t)i =
hS
1
(t), S
2
(t), . . . , S
n
(t), T
1
(t), T
2
(t), . . . , T
m
(t)i. All in-
stances over the S(t) represent source instances I(t),
while instances over T(t) J(t) are target instances. If
I (t) is a named source instance in S(t) and J (t) is a
ICEIS 2008 - International Conference on Enterprise Information Systems
542

named target instance the K = hI , J i is the named
instance over the schema hS(t), T(t)i. A de-
pendency named source-to-target dependencies over
hS(t), T(t)i of the form
(∀x(t))(φ
S(t)
(x(t)) → χ
T(t)
(x(t)))
where φ
S(t)
(x(t)) is an expression(formula),
with free variable x(t) = (x
1
(t), x
2
(t), . . . , x
k
(t))
of logical formalism over S(t) and χ
T(t)
(x(t))
is an expression(formula) with free variable
x(t) = (x
1
(t), x
2
(t), . . . , x
l
(t)) of logical formalism
over T(t). A dependency named target dependencies
over the target schema T(t) (the target dependencies
are different from those use for the source-to-target
dependencies).
Definition 3.1. A data exchange represent a 4-
tuple DE(t) = (S(t), T(t),
∑
st(t)
,
∑
t(t)
) with a source
schema S(t), a target schema T(t), a set
∑
st(t)
of
source-to-target dependencies and set
∑
t(t)
of target
dependencies.
For practical purposes each source-to-target de-
pendency
∑
st(t)
represents a tuple-generating-
dependency(tgd) of the form
(∀x(t))(φ
S(t)
(x(t)) → χ
T(t)
(x(t),y(t)))
where φ
S(t)(x(t))
represents a conjunction of atomic ex-
pression(formulas) over S(t) and χ
T(t)
(x(t),y(t)) rep-
resents a conjunction of atomic expression(formulas)
over T(t). A stored procedure named stored-
procedure-s over S(t), of the form
(∀x(t))(α
S(t)
(x(t)) → α
S(t)
(x(t)))
where α
S(t)
(x(t)) is a stored procedure over S(t) and a
stored procedure named stored-procedure-t over T(t),
of the form
(∀x(t))(β
S(t)
(x(t)) → β
S(t)
(x(t)))
where β
S(t)
(x(t)) is a stored procedure over T(t).
Definition 3.2. A schema mapping model represent a
6-tuple DE(t) = (S(t),
∑
α
S(t)
, T(t),
∑
β
T(t)
,
∑
st(t)
,
∑
t(t)
)
with a source schema S(t), all stored procedures over
S(t)
∑
α
S(t)
, a target schema T(t), all stored procedures
over T(t)
∑
β
T(t)
, a set
∑
st(t)
of source-to-target
dependencies and set
∑
t(t)
of target dependencies.
Our approach on symbolic modeling of data exchange
and schema mapping are:
Definition 3.3.
DB(t) :=
[
{db(t)|is− database(db(t))}
where db(t) is a database
Given a set of attributes Attr(t) and a set containing
sets of attribute values D(t), we define a column as a
function mapping an attribute into the set containing
its corresponding values:
ValColumn(t) : Attr(t) → D(t),
ValColumn(a(t)) :=
{d(t)|d(t) ∈ D(t)}
where d is a value for attribute ’a(t)’
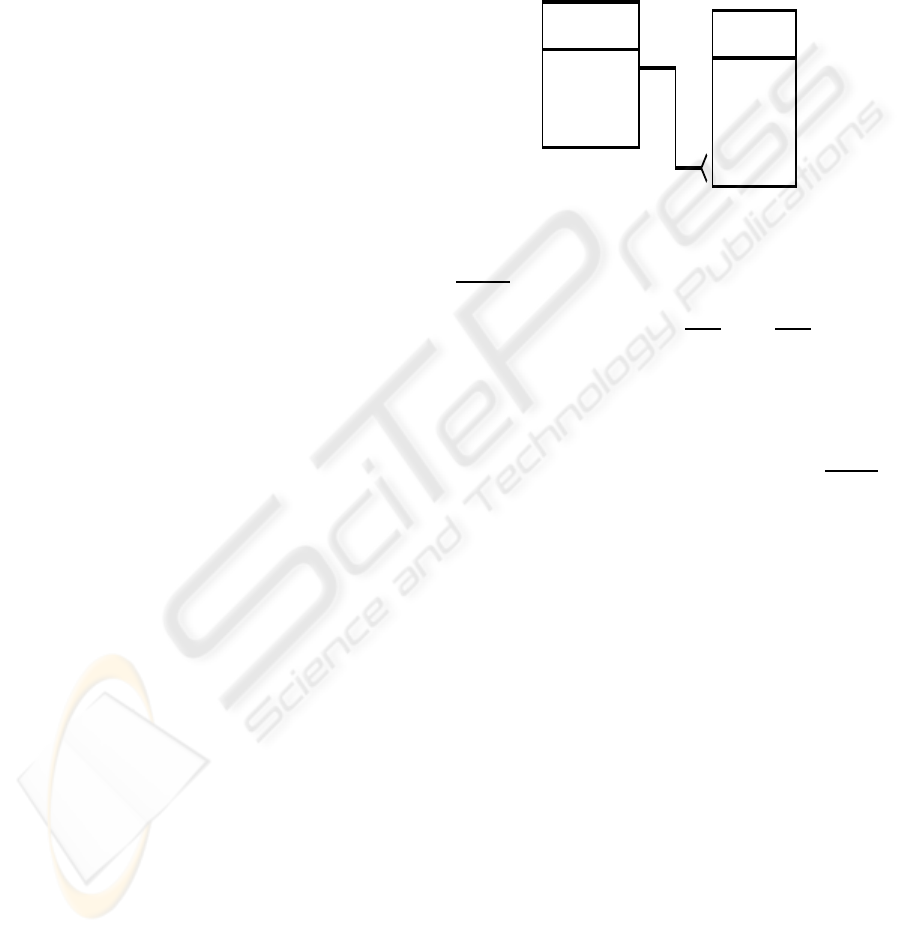
EMPLOYEE
#EmployeeID
Fname
LName
DeptID
DEPARTMENT
#DeptID
EmpN
Location
1
n
Figure 3: Database diagram for schema S.
Definition 3.4. Given a set of attributes Attr
i
(t), i =
1, ..., n the table T(t) from database is defined by:
is− Table(T
n(t),Attr
i
(t),i=1,...,n,D
i
(t),i=1,...,n
) ⇔
T(t) ∈
n
[
i=1
hAttr(t), ValColumn(Attr
i
(t))i
where Card(ValColumn(Attr
i
(t))) = nrw(t) =
NoRows(T(t))
the number of lines in table T(t), i = 1, ..., n,
n(t) = NoColT(t) the number of columns in the ta-
ble T(t).
In practice is posible to have S=T but S(t) 6= T(t)
that case is named by us data exchange for copy
schema mapping because all stored procedures over
S(t)
∑
α
S(t)
, and all stored procedures over T(t)
∑
β
T(t)
have the same semantic but diferent syntax in SQL
and Procedural Languages / SQL flavors on different
RDBMS.
We consider the folowing subdiagram with
schema S=(EMPLOYEE, DEPARTMENT) with EM-
PLOYEE (#EmlpoyeeID, FName, LName, Compa-
nyID), DEPT (#DeptID, EmpN, Location) see the
Database Diagram for schema S 3. In our case
S=T=(EMPLOYEE, DEPARTMENT). A trigger that
increments the number of employees each time a new
person is hired, that is, eachtime a new row is inserted
into the table EMPLOYEE has the same semantic in
S and T but different syntax in different Procedural
Language over different SQL flavors.
SCHEMA MAPPING FOR RDBMS
543

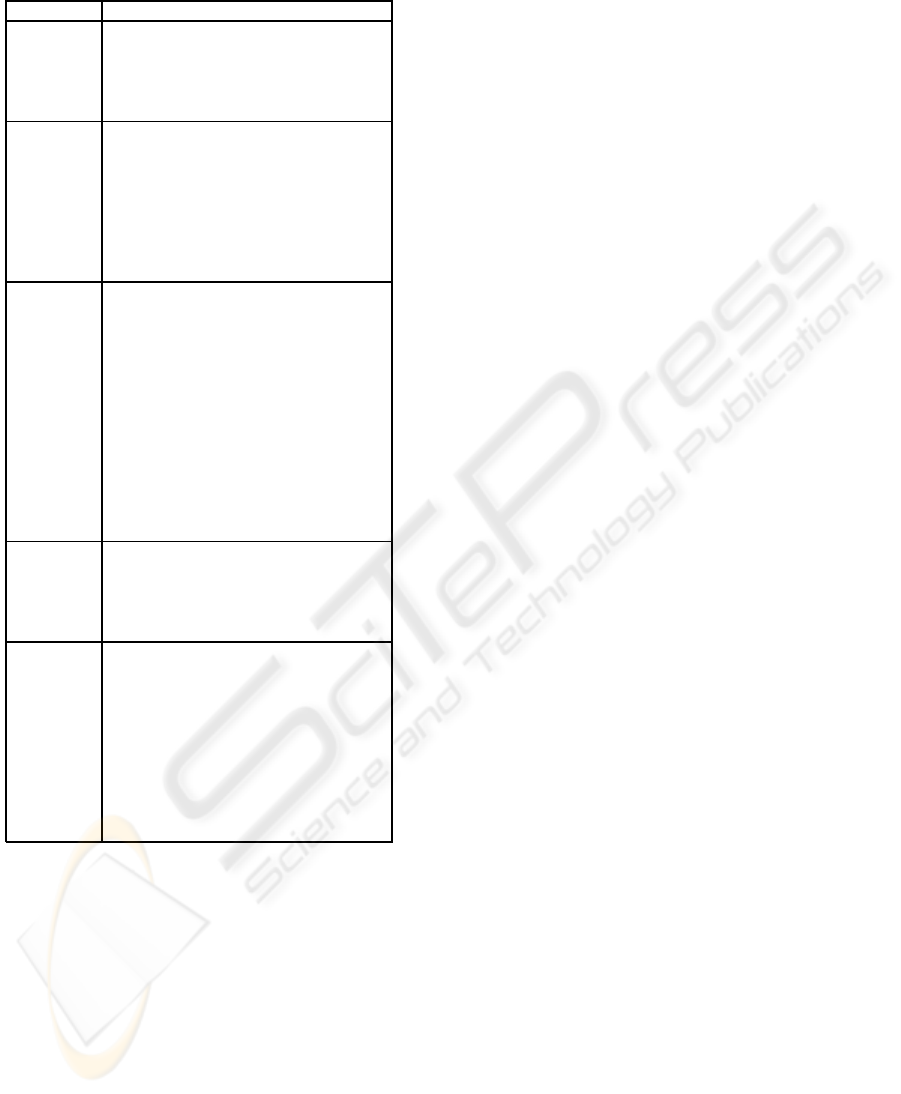
Table 1: The triggers when a new person is hired.
RDBMS STORED PROCEDURES
IBM DB2 CREATE TRIGGER NEWHIRED
AFTER INSERT ON EMPLOYEE
FOR EACH ROW MODE DB2SQL
UPDATE DEPT
SET EmpN = EmpN + 1
Oracle CREATE TRIGGER NEWHIRED
AFTER INSERT ON EMPLOYEE
BEGIN
UPDATE DEPT
SET EmpN = EmpN + 1
WHERE
EmlpoyeeID=:New.EmlpoyeeID
END;
Sybase CREATE TRIGGER ”NEWHIRED”
AFTER INSERT OF EmlpoyeeID
ON EMPLOYEE
REFERENCING OLD AS EO
NEW AS EN
FOR EACH ROW
BEGIN
UPDATE DEPT
SET
DEPT.EmpN = DEPT.EmpN + 1
WHERE
EMPLOYEE.EmlpoyeeID=EN
END
MySQL CREATE TRIGGER NEWHIRED
AFTER INSERT ON EMPLOYEE
FOR EACH ROW
UPDATE DEPT
SET EmpN = EmpN + 1
Postgres CREATE FUNCTION EmpA()
BEGIN
UPDATE FIRMA SET
EmpN = EmpN + 1;
END;
LANGUAGE ’plpgsql’ VOLATILE
CREATE TRIGGER NEWHIRED
AFTER INSERT ON EMPLOYEE
FOR EACH ROW
EXECUTE PROCEDURE EmpA();
4 CONCLUSIONS
In this paper we proposed data exchange metamodel
for copy schema mappings that describes the conver-
sion of Schema Model from one Platform-Specific
Model to other Platform-Specific Model according
to Meta-Object Facility-Query/Verify/Transform in
dynamical mode. A prototype application, named
ANCUTZA (ANalytiCal User Tool ZAmolxys)-
universal SQL and Procedural Language/SQL trans-
lator-for data exchange metamodel is in project phase
in idea to support a part of SQL flavors on different
RDMBS.
ACKNOWLEDGEMENTS
The authors would like to thank for the support to
PhD. Zsuzsanna-Katalin Szabo, Dean at Faculty of
Economics, Law, and Administrative Science from
Petru Maior Univerisity of Tg-Mures¸.
REFERENCES
Andreica, A., Stuparu, D., and Mantu, I. (2005). Symbolic
modelling of database representations. In 7
th
Inter-
national Symposium on Symbolic and Numeric Algo-
rithms for Scientific Computing. IEEE Computer So-
ciety Press, pp. 59-62.
Berri, C. and Vardi, M. (1984). A proof procedure for data
dependencies. In Journal of Assoc. Comput. Mach.
pp. 718-741.
Chomsky, N. (1956). Three models for the description of
language. In IRE Transactions on Information Theory.
pp. 113-123.
Fagin, R. (2007). Inverting schema mapping. In Transac-
tions on Databases Systems. ACM, 30, pp. 1-53.
Fagin, R., Kolaitis, P., Miller, R., and Popa, L. (2003). Data
exchange: semantics and query answering. In TEM-
PLATE’06, 1st International Conference on Template
Production. ELSEVIER, 336, 1, pp. 89-124.
Fagin, R., Kolaitis, P., and Popa, L. (2005a). Data exchange:
Getting to the core. In Transactions on Databases Sys-
tems. ACM, 30, pp. 994-1055.
Fagin, R., Kolaitis, P., and Popa, L. (2005b). Schema map-
pings: Second-order dependencies to the rescue. In
Transactions on Databases Systems. ACM, 30, pp.
994-1055.
Fagin, R. and Nash, A. (TheStructure of Inverses in Schema
Mappings). Inverting schema mapping. In Transac-
tions on Databases Systems. IBM Research Report,
RJ10425(A0712-004) 1-9.
Miller, R., Haas, L., and Hernandez, M. (2000). Schema
mapping as query discovery. In Proceedings of
the International Conference on Very large Data
Bases(VLDB). SPRINGER VERLAG, pp. 77-88.
Popa, L., Velegrakis, Y., Miller, R., Hernandez, M., and Fa-
gin, R. (2002). Translating web data. In Proceedings
of the International Conference on Very Large Data
Bases (VLDB). SPRINGER VERLAG, pp. 598-609.
Pranevicius, H. (2001). Translating web data. In The Use
of Aggregate and Z Formal Methods for Specification
and Analysis of Distributed Systems. Lecture Notes
in Computer Science (LNCS), SPRINGER VERLAG,
2151, pp. 253-266.
Shu, N., Housel, B., Taylor, R., Ghosh, S., and Lum, V.
(1977). Express: A data extraction, processing, and
restructuring system. In TEMPLATE’06, 1st Inter-
national Conference on Template Production. ACM
Transaction on Database System, pp. 134-174.
ICEIS 2008 - International Conference on Enterprise Information Systems
544