NURSE SCHEDULING BY COOPERATIVE GA WITH

VARIABLE MUTATION OPERATOR

Shin-ya Uneme, Hikaru Kawano and Makoto Ohki

Department of Information and Electronics, Graduate School of Engineering, Tottori University, Japan

Keywords: Cooperative Genetic Algorithm, Variable Mutation Operator, Nurse Scheduling.

Abstract: This paper proposes an effective mutation operator for the cooperative genetic algorithm (CGA) to solve a

nurse scheduling problem. The nurse scheduling is very complex task for a clinical director in a general

hospital. Even veteran director requires one or two weeks to create the schedule. Besides, we extend the

nurse schedule to permit the change of the schedule. This permission has explosively increased computation

time for the nurse scheduling. We propose the new mutation operator to solve the problem. The CGA with

the new mutation operator has brought surprising effective results.

1 INTRODUCTION

A general hospital consists of several sections such

as the internal medicin department or the pediatrics

department. About fifteen to thirty nurses are

working in each section. A clinical director of the

section arranges a shift schedule of all the nurses in

the section every month. Constituting the nurse

schedule (Ikegami 2001), or the nurse scheduling, is

very complex task for the clinical director. In our

investigation, even a veteran director needs one or

two weeks for the nurse scheduling. Then, computer

software for the nurse scheduling has recently come

to be used in the hospital.

In conventional ways (Kawanaka 2002, Itoga,

2003) using the cooperative genetic algorithm

(CGA), a crossover operator is only employed for

the optimization, because it does not lose

consistency between chromosomes. A mutation

operator is considered to lose the consistency. In

contrast, we have proposed an effective mutation

operator for the CGA which does not lose

consistency of the schedule (Ohki, 2007). The CGA

with the mutation operator has brought surprising

effective results which has never been brought by

the conventional algorithm. On the other hand,

Burke performs a lot of interesting studies about the

nurse roster at the large hospital in the Europe

(Burke 2004).

In this paper, we rearrange the nurse scheduling

problem to permit the change of the schedule. This

permission has complicated a problem and

explosively increased computation time for the nurse

scheduling. Now, we need a new technique to make

the nurse scheduling speed up. We propose a new

mutation operator to solve this problem.

2 OVERVIEW OF NURSE

SCHEDULING

On the nurse scheduling, we have to consider many

requirements (Ohki, 2007), such as duty load of each

nurse, fairness of assignment of day time and night

duty, intensiveness of night duty. We have arranged

these many requirements for twelve penalty

functions. These twelve penalty functions are

summarized in one penalty function, E(g), for

performing a population.

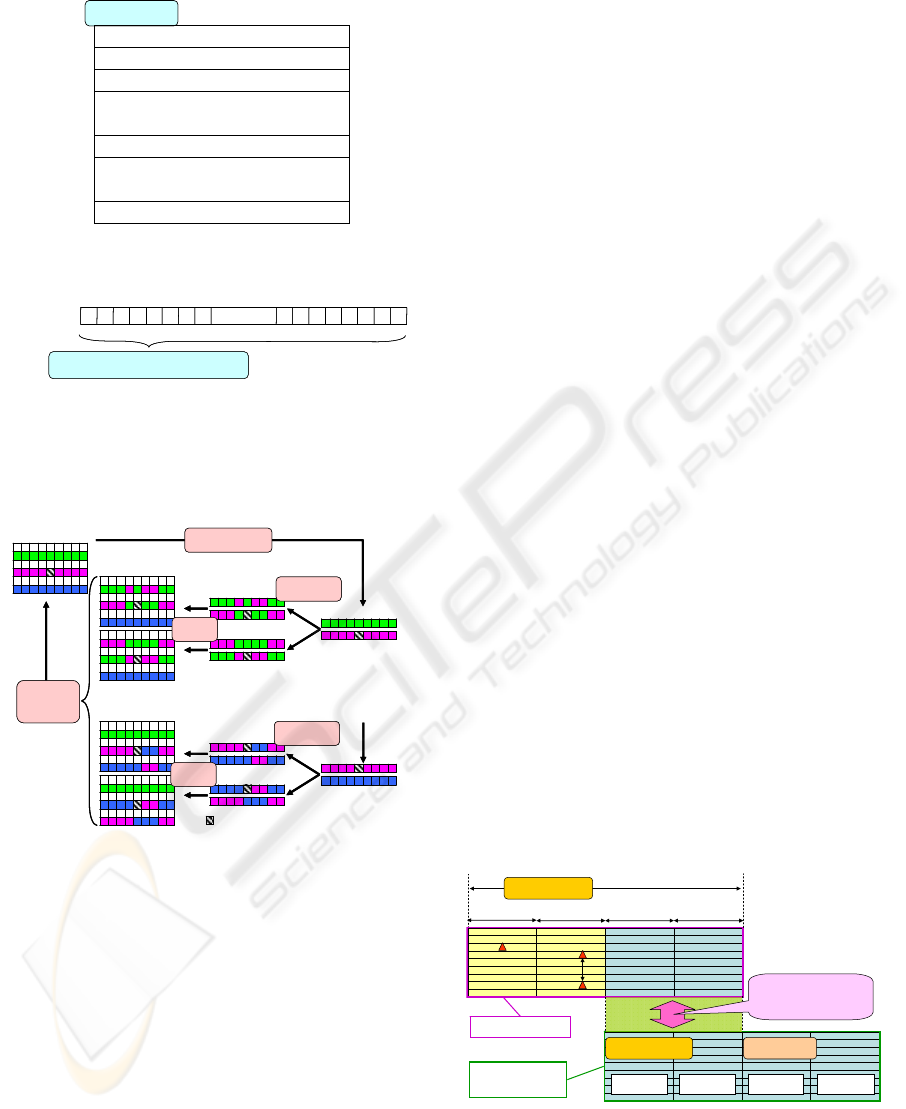
In the CGA, the population represents the whole

nurse schedule of one month as shown in Fig.1

(Ohki, 2007). Each individual is defined in a

chromosome code which shows one-month schedule

of a nurse. The individual consists of the duty

symbols as shown in Fig.2. The duty sequence

consists of thirty symbols, since one month includes

thirty days in this practical example.

Initially, the population is randomly generated as

satisfying the necessary number of nurses at every

duty time slot. In this paper, the necessary number of

nurses is specified as ten, six and five for the day

time duty on a week day, Saturday and Sunday

respectively, three for the semi night duty and three

249

Uneme S., Kawano H. and Ohki M. (2008).

NURSE SCHEDULING BY COOPERATIVE GA WITH VARIABLE MUTATION OPERATOR.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 249-252

DOI: 10.5220/0001694802490252

 SciTePress

for the mid night duty respectively.

・

individual set

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

・

individual set

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

duty schedule of nurse n

for one month

・

Figure 1: Population is composed of one-month schedules

of each nurse.

duty schedule for one month

・・・・・

MRTSHHH HMRS

nurse n

DD DDD

duty schedule for one month

・・・・・

MRTSHHH HMRS

nurse n

DD DDD

Figure 2: An individual coded in chromosome. The

symbols, D, S, M, H, T, R denote daytime duty, semi-

night duty, mid-night duty, given holiday, training and

requested holiday respectively.

select parents

crossover

・

※

denotes fixed duty, for example,

meetin

dut

and re

uested holida

crossover

・

individual set

pareto

selection

return

select parents

crossover

・

※

denotes fixed duty, for example,

meetin

dut

and re

uested holida

crossover

・

individual set

pareto

selection

return

Figure 3: Basic optimization cycle of the CGA only

employs with the crossover operator.

An overview of the optimization only with the

crossover operator is shown by Fig.3. First, two

hundreds pairs of the individual are selected as

parents for the crossover. One of the pair is selected

from the population under the roulette selection

manner. The roulette selection gives an individual

with higher penalty. This manner tends to select the

worse individual. Another one of the parent pair is

randomly selected from the population. Exchanging

parts of the individuals divided at two points of the

chromosome, two new pairs of individual are

generated as children. This exchanging process does

not exchange the fixed duties, such as the meeting,

the training and the requested holiday. These child

pairs are temporally returned to the original nurse

position respectively. The temporal population with

the children is performed by the penalty function.

After all the temporal populations have been

performed, one pair giving the smallest penalty is

selected for the next generation.

3 EXTENSION OF NURSE

SCHEDULING

In this research, we extend the nurse schedule

problem to permit the change of the schedule. In fact,

one or two changes appear in the past duty days of

the current month. We consider the following cases:

(1) A certain nurse took a holiday on a duty date,

(2) A certain nurse worked in a holiday fixed day,

(3) Two nurse’s shift were changed,

(4) Acertain nurse resigned from his/her job,

(5) A certain nurse increased newly.

When these rose in the past date, the number of day

time, semi-night and mid-night duties of some

nurses must be changed. Although these duty days

must be fair for all nurses in the section, nursing

level must be kept at each duty time slot. Then the

director has to consider the change of the schedule.

In this paper, we asume that a change has been

occurred in the past two weeks and handle the

optimization of coming four weeks as shown in

Fig.4. In the optimization of the four weeks, a new

penalty function is defined as F

. This penalty

counts the differences between duty symbols on the

and 4

weeks of the original schedule and them

of the newly optimizaed schedule. Therefor, the total

penalty function, E(g), is defined as the summation

of thirteen penalty functions.

week

week 3

week 4

week

original schedule

week 4

week

next month

current month

newly optimized

schedule

new penalty about

defference F

current month

Figure 4: Permission of the change of the schedule in the

past two weeks. The red triangle denotes the schedule

change.

ICEIS 2008 - International Conference on Enterprise Information Systems

250

4 VARIABLE MUTATION

OPERATOR

We have proposed the CGA with the mutation

operator for the nurse scheduling in the manuscript

(Ohki, 2007). When the conventional nurse

scheduling is handled, the technique has given

results good enough. On the other hand, the

extension of the nurse scheduling to permit its

change complicates the problem and explosively

increases computation time. The conventional

technique is not effective enough for the extended

problem. Then we propose a new mutation operator.

We have examined the extended nurse

scheduling using the conventional mutation. The

conventional mutation operator whose mutation

interval is defined as 150 generations works most

effective. Since the mutation interval is fixed, the

mutation is executed at the same frequency anytime.

When the optimization stagnates long time, the

mutation should be executed. In contrast, when the

optimization goes steadily, the mutation should not

be executed. An optimization speed is defined as

follows to explain progress of the optimization,

∑

−

−=

)(

igE

, (1)

)()1()( gAgAgV −

−

, (2)

100

200

300

400

500

600

10200 10700 11200 11700 12200 12700 13200

generation g

penalty E & average

0.5

1.5

optimization speed

(a)10200-13200

100

200

300

400

500

600

384000 384500 385000 385500 386000 386500 387000

generation g

penalty E & average

0.5

1.5

optimization speed

(b)384000-387000

100

200

300

400

500

600

993600 994100 994600 995100 995600 996100 996600

generation g

penalty E & average

0.5

1.5

optimization speed

Figure 5: The total penalty function, E(g), the average,

A(g), and the optimization speed, V(g) in the beginning (a),

the middle (b) and the end (c) of the optimization using

the conventional mutation operator respectively.

where N

denotes the number of generations for

average. Examples of the value of the total penalty

function, E(g), the average, A(g), and the

optimization speed, V(g), are shown in Fig.5.

Though the optimization goes well, the mutation is

executed too early in some cases. In some other

cases, though the optimization has already stagnated,

the mutation is executed too late.

We propose the variable mutation operator to

improve such an obstruction. The new operator

mutates the schedule when the optimization speed

satisfies the following condition,

)(gV

where

denotes a threshold value. This condition

means that the optimization has stagnated.

In some cases, the optimization does not advance

for several generations after the mutation, as shown

in Fig.5. The mutation does not work during G

generations after the mutation is executed once. We

call such generations the guard interval. The

mutation is executed in the appropriate generation

by means of such a technique.

5 PRACTICAL EXPERIMENTS

Here, we set a problem as follows. Let the number

of nurses and the number of duty days be twenty-

three and twenty-eight respectively. We handle a

case when one change has been occurred in the past

two weeks. This situation is one of typical and

practical case in Japanese hospital which we have

investigated.

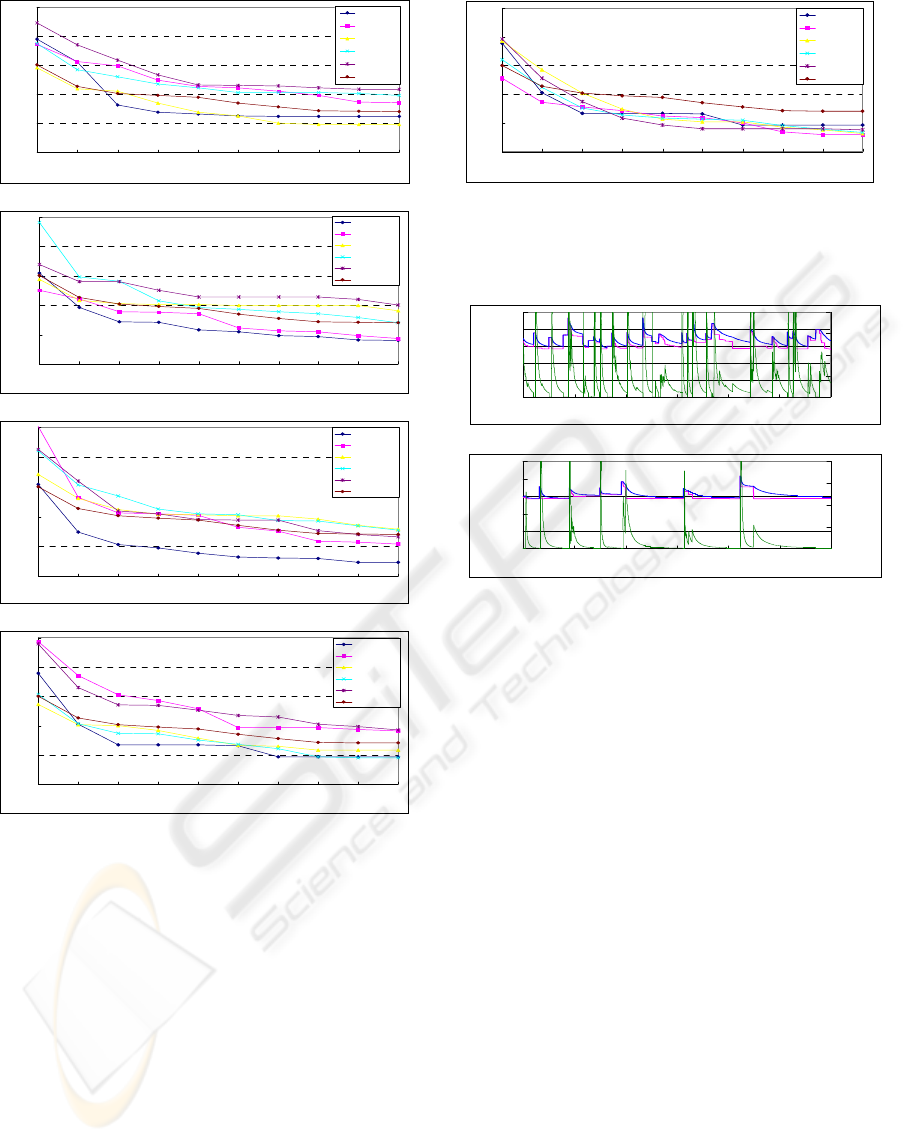
First, we have considered about the guard

interval. We tried the extended nurse scheduling by

using the variable mutation operator under several

conditions as shown in Fig.6. This result shows that

the guard interval can be easily decided in wide

range. Here, we decide it as fifty.

Next, we have considered about the threshold,

The variable mutation operator with the guard

interval, 50, and the threshold, 0.1, has given the

best result as shown in Fig.6, (d). We have tried

several thresholds less than 0.1 as shown in Fig.7.

This result shows that the threshold can be easily

decided in wide range less than 0.1. The variable

mutation operator with any values of threshold has

given better results than the conventional one.

Finally, we have examined the extended nurse

scheduling using the variable mutation operator.

The mutation is executed in appropriate generations

as shown in Fig.8. This means that the variable

mutation operator works effectively.

NURSE SCHEDULING BY COOPERATIVE GA WITH VARIABLE MUTATION OPERATOR

251

380

385

390

395

400

405

100 200 300 400 500 600 700 800 900 1000

generation g [10^3]

penalt

ε=0.1

ε=0.25

ε=0.3

ε=0.4

ε=0.5

co nventiona l

(a) G

=10

380

385

390

395

400

405

100 200 300 400 500 600 700 800 900 1000

generation g [10^ 3]

penalt

ε =0.1

ε =0.25

ε =0.3

ε =0.4

ε =0.5

conventional

(b)

=20

380

385

390

395

400

405

100 200 300 400 500 600 700 800 900 1000

generation g [10^ 3 ]

penalt

ε =0.1

ε =0.25

ε =0.3

ε =0.4

ε =0.5

conventional

=30

380

385

390

395

400

405

100 200 300 400 500 600 700 800 900 1000

generation g [10^3]

penalt

ε =0.1

ε =0.25

ε =0.3

ε =0.4

ε =0.5

co nventional

(d)

=50

Figure 6: Comparison among optimization results with

several values of the guard interval. We have tried the

optimization under each condition ten times. We took

average of each ten trials.

6 CONCLUSION

In this paper, we have extended the nurse scheduling

problem to permit the change of the schedule. This

extension complicates the problem and explosively

increases computation time. To improve this

difficulty, the new mutation operator with variable

interval is proposed. The variable mutation operator

has several parameters which can be defined in wide

range. This means that the new technique possesses

high versatility.

380

385

390

395

400

405

100 200 300 400 500 600 700 800 900 1000

generation g [10^3]

penalt

ε=0.1

ε=0.08

ε=0.06

ε=0.04

ε=0.02

conventional

Figure 7: Results of the variable mutation operator with

the threshold less than 0.1. We have tried the optimization

under each condition ten times. We took average of each

ten trials.

100

200

300

400

500

600

506000 506500 507000 507500 508000 508500 509000

gen eratio n g

penalty E & average

0.5

1.5

optimization speed

(a)

07.0],509000,506000[ =

∈

100

200

300

400

500

600

603000 603500 604000 604500 605000 605500 606000

gen eratio n g

penalty E & average

0.5

1.5

optimization speed

(b)

01.0],606000,603000[ =

∈

Figure 8: The total penalty function, E(g), the average,

A(g), and the optimization speed, V(g), of the optimization

using the variable mutation operator respectively.

REFERENCES

Ikegami, A. 2001, Algorithms for Nurse Scheduling, Proc.

of 11th Intelligent System Symposium.

Kawanaka, S., Yamamoto Y., Yoshikawa D., Shinogi T.

and Tsuruoka N., 2002, Automatic Generation of

Nurse Scheduling Table Using Genetic Algorithm,

Trans. on IEE Japan, Vol.122-C.

Itoga, T., Taniguchi N., Hoshino Y. and Kamei K., 2003,

An Improvement on Search Efficiency of Cooperative

GA and Application on Nurse Scheduling Problem,

Proc. of 12th Intelligent System Symposium.

Ohki, M., Uneme, S., Hayashi, S. and Ohkita, M., 2007,

Effective Genetic Operators of Cooperative Genetic

Algorithm for Nurse Scheduling, Proc. of 4

International Conference on Informatics in Control,

Automation and Robotics.

Burke E.K., De Causmaecker P., Berghe G. V., 2004,

Novel Meta-heuristic Approaches to Nurse Rostering

Problems in Belgian Hospitals, Models and

Performance Analysis, CRC Press.

ICEIS 2008 - International Conference on Enterprise Information Systems

252