A NEW APPROXIMATE REASONING BASED ON SPMF
Dae-Young Choi
Dept. of MIS, YUHAN College, Koean-Dong, Sosa-Ku, Puchon City
Kyungki-Do, South Korea
Keywords: Approximate reasoning, Linear time complexity.
Abstract: A new approximate reasoning based on standardized parametric membership functions (SPMF) is proposed.
It provides an efficient mechanism for approximate reasoning within linear time complexity.
1 INTRODUCTION
Approximate reasoning is generally expressed in the
form of the following syllogism :
Rule : IF X is A THEN Y is B
Observation : X is A′ (1)
Conclusion : Y is B′
where X and Y are linguistic variables, and A, B and
A′ are fuzzy subsets defined in the universe of
discourse U, V and U, respectively. Generally, in
order to obtain the deduction of conclusions from
observations and rules in a knowledge base, there
are three alternative ways of doing this in fuzzy sets
framework: truth value restriction (Zadeh, 1975),
compositional rule of inference (CRI) (Zadeh, 1973)
and an approximate analogical reasoning schema
(AARS) (Turksen and Zhong, 1988). The CRI has
been more widely accepted and applied in
development studies. The CRI is essentially based
on matrix operation. The effect of such matrix
operations on membership function value
propagation is not conceptually clear. Some of its
undesirable consequences were pointed out in
(Mizumoto, 1985, Turksen and Zhong, 1988). It has
major flaws that it does not satisfy the modus ponens.
That is, when A′=A, the deduced B′ is obtained as
follows : μ
B′
= (1+μ
B
)/2 ≠ μ
B
. This inference result
indicates that the CRI does not satisfy the modus
ponens, i.e., (A∧(A→B))→B, which is quite
reasonable demand in the approximate reasoning. In
addition, ‘indetermination’ part of the consequence
occurs because of the incompatibility between the
membership functions of A in the premise of rule
and A′ from observation. This incompatibility
happens when the insignificant part (i.e., the zero
membership range) of A includes that of A′ (Chang
et al., 1991). In the meantime, the AARS uses the
term similarity to express the semantics of inference.
Here, the similarity of two fuzzy sets is expressed by
the following equation: SM=(1+DM)
-1
where
SM∈[0,1]. That is, the similarity measure (SM) is
obtained by using the distance measure (DM).
However, it did not define clearly how to obtain the
DM. In addition, it did not define clearly the
modification function (MF) that plays an important
role in the approximate reasoning. To handle these
problems, a new approximate reasoning based on
SPMF is proposed.
2 SPMF
Let A be a fuzzy set for a linguistic term and be a
subset of the universal set X, then, for x∈X, a
triangular-type membership function can be
represented by using 3 points μ
A
(x
L
, x
M
, x
H
), where
x
L
<x
M
<x
H
, and if the result of this membership
function is normalized to [0, 1] then μ
A
(x
L
, x
M
, x
H
) =
0 for every x∈[-∞, x
L
]∪[x
H
, ∞] and μ
A
(x
L
, x
M
, x
H
) = 1
at x
M
. A trapezoidal-type can be represented by using
4 points μ
A
(x
L
, x
I
1
, x
I
2
, x
H
), where x
L
<x
I
1
<x
I
2
<x
H
, and if
the result of this membership function is normalized
to [0, 1] then μ
A
(x
L
, x
I
1
, x
I
2
, x
H
) = 0 for every x∈[-∞,
x
L
]∪[x
H
, ∞] and μ
A
(x
L
, x
I
1
, x
I
2
, x
H
) = 1 at [x
I
1
, x
I
2
]. A
more comprehensive study of SPMF can be found in
(Chang et al., 1991).
383
Choi D. (2008).
A NEW APPROXIMATE REASONING BASED ON SPMF.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 383-386
DOI: 10.5220/0001669703830386
Copyright
c
 SciTePress

3 THE PROPOSED METHOD
A new approximate reasoning based on SPMF
makes the DM to compare two fuzzy sets in the
pattern matching phase, and then the DM is used
to construct the MF. The MF will adjust the right
side of the rule in the consequent deducing phase.
We first consider a simple rule case where only
one observation A′ and one simple rule as in Eq.
(1).
3.1 Distance Measure (DM)
Based on their behavioral experiment (Zwick et al.,
1987), they recommended the five good DM
between fuzzy subset A and B of a universe of
discourse U. We note that the five good DM
concentrate their attention on a single value rather
than performing some sort of averaging or
integration. We know that the reduction of
complicated membership functions to a single ‘slice’
may be the intuitively natural way for human beings
to combine and process fuzzy concepts. Moreover,
we know that the DM between two fuzzy subsets can
be efficiently represented by a limited number of
features. From these ideas, we define the DM based
on the structure of the SPMF.
(1) Triangular-type Membership Functions
If the antecedent A of a rule is represented by A =
(x
L
, x
M
, x
H
) and an observation A′ is represented by A′
= (x
L
′, x
M
′, x
H
′), then each DM is obtained regarding
its corresponding 3 points, respectively.
DM
L
= x
L
′ - x
L
DM
M
= x
M
′-x
M
(2)
DM
H
= x
H
′ - x
H
(2) Trapezoidal-type Membership Functions
If the antecedent A of a rule is represented by A =
(x
L
, x
I
1
, x
I
2
, x
H
) and an observation A′ is represented
by A′ = (x
L
′, x
I
1
′, x
I
2
′, x
H
′), then each DM is obtained
regarding its corresponding 4 points, respectively.
DM
L
= x
L
′ - x
L
DM
I
1
= x
I
1
′ - x
I
1
(3)
DM
I
2
= x
I
2
′ - x
I
2
DM
H
= x
H
′ - x
H
3.2 Pattern Matching
The pattern matching is achieved through the use of
the least distance measure (LDM) between the
observed fact and the antecedent of a rule.
(1) Triangular-type Membership Functions
LDM
p
= min {DM
L
+DM
M
+DM
H
} for all rules in a
rule base. (4)
(2) Trapezoidal-type Membership Functions
LDM
I
= min {DM
L
+ DM
I
1
+ DM
I
2
+ DM
H
} for
all rules in a rule base. (5)
Thus, the rule with LDM
p
or LDM
I
is selected in a
rule base.
3.3 Modification Functions (MF)
In the proposed method, a rule R
i
: A
i
→ B
i
is to be
fired with each MF that modifies the consequent B
i
of the rule R
i
. We construct each MF based on its
corresponding DM in Eqs. (2), (3). When deducing a
consequent, the MF enables us to bypass the matrix
operations of CRI. Each MF is achieved by using the
following formulas :
(1) Triangular-type Membership Functions
Let the maximum support interval (MSI) of two
fuzzy subsets (i.e., A, A′) represented by using the
triangular-type membership functions be [x
LL
, x
MH
],
where x
LL
is derived from min {x
L
, x
L
′} and x
MH
is
derived from max {x
H
, x
H
′}, and let the distance of
MSI of two fuzzy subsets (DMSI) be |x
MH
-x
LL
|, then
each MF is obtained regarding its corresponding 3
points, respectively.
MF
L
= (1+ (DM
L
/DMSI))
MF
M
= (1+ (DM
M
/DMSI)) (6)
MF
H
= (1+ (DM
H
/DMSI)) where each DM
is derived from Eq. (2).
(2) Trapezoidal-type Membership Functions
Let the MSI of two fuzzy subsets (i.e., A, A′)
represented by using the trapezoidal-type
membership functions be [x
LL
, x
MH
], where x
LL
is
derived from min {x
L
, x
L
′}, and x
MH
is derived from
max {x
H
, x
H
′}, and let the DMSI of two fuzzy subsets
be |x
MH
-x
LL
|, then each MF is obtained regarding its
corresponding 4 points, respectively.
MF
L
= (1+ (DM
L
/DMSI))
MF
I
1
= (1+ (DM
I
1
/DMSI)) (7)
MF
I
2
= (1+ (DM
I
2
/DMSI))
MF
H
= (1+ (DM
H
/DMSI)) where each DM is
derived from Eq. (3).
We can determine the overall MF(OMF) by
averaging all MF in Eqs. (6) or (7), respectively.
OMF = avg{all MF(A, A′)} where the all MF(A, A′)
ICEIS 2008 - International Conference on Enterprise Information Systems
384

are derived from Eqs.(6) or (7), respectively. (8)
In Eq. (8), we consider a simple rule case where only
one observation A′ and one simple rule in the form
‘IF X is A THEN Y is B’. The construction of MF is
subjective in (Turksen and Zhong, 1988). To handle
this problem we suggest the efficient OMF based on
the structure of the SPMF.
3.4 Deducing a Consequent
It is assumed that we consider a simple rule case
where only one observation A′ and one simple rule
in the form ‘IF X is A THEN Y is B’. Let B be a
fuzzy subset of the linguistic variable ‘Y’ and be
represented by the SPMF then, for
∀
y∈Y, the
linguistic value B can be represented by (y
L
, y
M
, y
H
)
or (y
L
, y
I
1
, y
I
2
, y
H
) in the triangular-type and
trapezoidal-type membership functions, respectively.
In the proposed method, we construct the deduced
consequent B′ by applying the OMF to B.
(1) Triangular-type Membership Functions
y
L
′ = OMF × y
L
y
M
′ = OMF × y
M
(9)
y
H
′ = OMF × y
H
where the OMF is
derived from Eq. (8).
(2) Trapezoidal-type Membership Functions
y
L
′ = OMF × y
L
y
I
1
′ = OMF × y
I
1
(10)
y
I
2
′ = OMF × y
I
2
y
H
′ = OMF × y
H
where the OMF is
derived from Eq. (8).
The OMF obtained in the pattern matching phase is
applied to the points such as y
L
, y
H
, etc, in the
consequent deducing phase as in Eqs. (9), (10).
Definition 1. According to Eqs. (2), (3), (6)-(8), in
case of a positive dependency (e.g., ‘good → big’,
see Example 1) between A and B in a rule, the
directionality of modification in the consequent
deducing phase is determined.
Case 1 : If OMF < 1, then the left shift with OMF
occurs regarding all points such as y
L
, y
H
, etc.
Case 2 : If OMF = 1, then no shift occurs. As a
special case, for a pair (A, A′), if all DM in Eqs. (2)
or (3) is zero, then the exact matching occurs
between the observed fact A′ and the antecedent A
of a rule.
Case 3 : If OMF > 1, then the right shift with OMF
occurs regarding all points such as y
L
, y
H
, etc.
On the contrary, in case of a negative dependency
(e.g., ‘high weight → low speed’) between A and B
in a rule, the directionality of modification in the
consequent deducing phase is determined reversely.
We note that when the special case of Case 2 of the
Definition 1 occurs (i.e., A = A′), the reasoning
result of the proposed method becomes B′ = B. This
is one of the advantages of the proposed method
over CRI. In other words, the proposed method
satisfies the modus ponens but the CRI does not
satisfy the modus ponens.
Example 1. We consider a simple rule case where
only one observation A′ and one simple rule in the
form ‘IF X is A THEN Y is B’. It is assumed that the
selected rule is ‘IF economic conditions were good
THEN the earning was big’, and one observation is
‘economic conditions are good′’. We assume that the
stockholder defines fuzzy subsets regarding the
goodness of the linguistic variable economic
conditions in the interval [0, 100] by using the
trapezoidal-type.
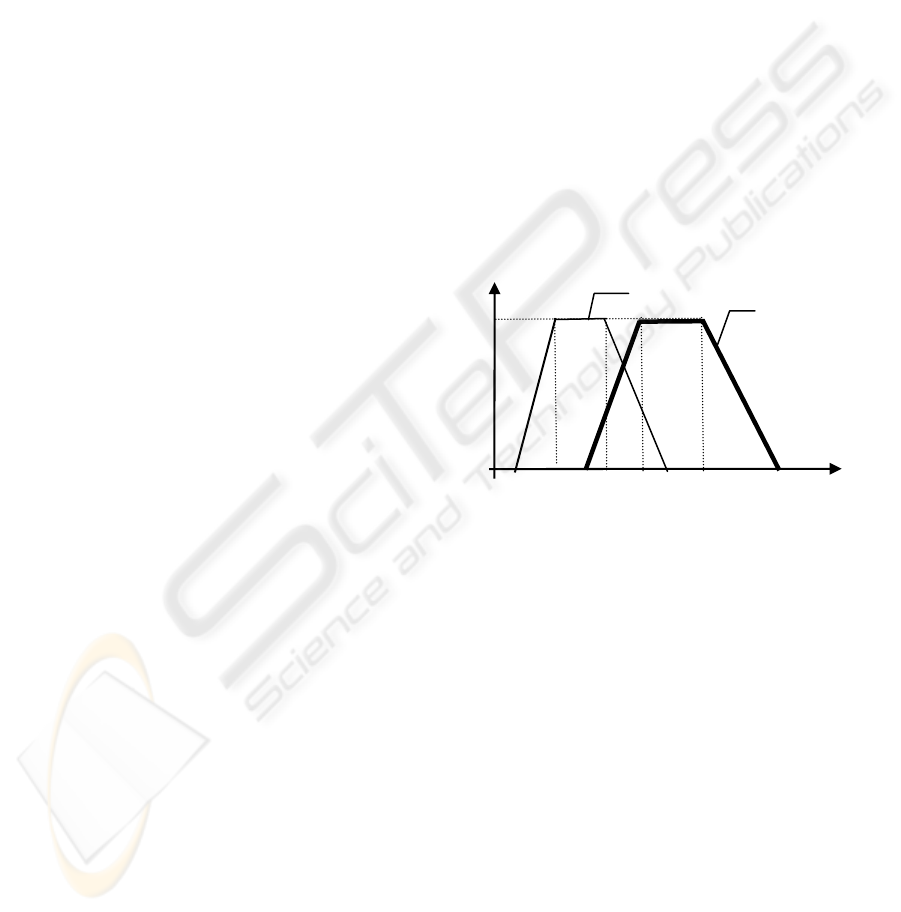
μ
1
80 85 88 90 92 95 96 100 X
Figure 1: An example of fuzzy subsets regarding the
goodness of economic conditions (X).
In Figure 1, the antecedent A of the selected rule is
assumed to be ‘good’, whereas the observation A′ is
assumed to be ‘good′’. In this case, each MF is
computed by using Eq. (7).
MF
L
= (1+ ((88-80)/(100-80)) = (1 + (8/20)) = 1.4.
MF
I
1
= (1+ ((92-85)/(100-80)) = (1 + (7/20)) = 1.35.
MF
I
2
= (1+ ((96-90)/(100-80)) = (1 + (6/20)) = 1.3.
MF
H
= (1+ ((100-95)/(100-80)) = (1 + (5/20)) = 1.25.
Thus, we obtain the OMF = (1.4+1.35+1.3+1.25)/4 =
1.33 by using Eq. (8). In the meantime, we assume
that the stockholder defines the fuzzy subset ‘big
earning’ as in Figure 2. Using Eq. (10), we construct
the deduced consequent B′ by applying the OMF to
B as in Figure 2.
y
L
′ = OMF × y
L
= 1.33 × $10 = $13.3.
y
I
1
′ = OMF × y
I
1
= 1.33 × $12 = $15.96.
y
I
2
′ = OMF × y
I
2
= 1.33 × $13 = $17.29.
y
H
′ = OMF × y
H
= 1.33 × $15 = $19.95.
Thus, we obtain the deduced consequent B′, i.e., the
Good
Goo
d
′
A NEW APPROXIMATE REASONING BASED ON SPMF
385

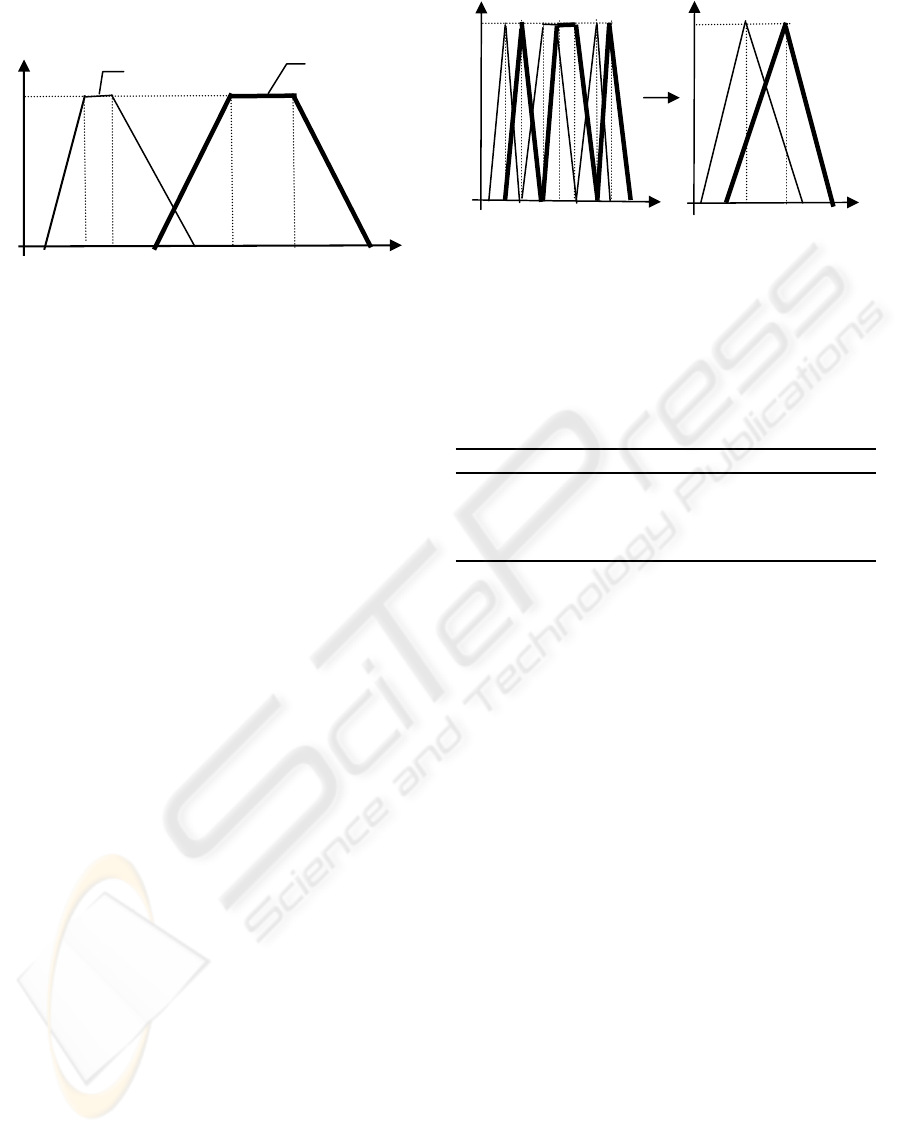
deduced earning = (y
L
′, y
I
1
′, y
I
2
′, y
H
′) = (13.3, 15.96,
17.29, 19.95).
μ
1
10 12 13 13.3 15 15.96 17.29 19.95 Y
Figure 2: An example of fuzzy subsets.
Now, we consider the composite rules with ‘OR’ and
‘AND’ connectives.
(1) ‘OR’ Composition
Given a rule with the following format : [A
i
1
OR A
i
2
OR …OR A
i
K
] → B
i
, it can be decomposed into
simple rules as A
i
1
→ B
i
, A
i
2
→ B
i
, … , A
i
K
→ B
i
,
and can be treated as individual simple rules,
respectively (Turksen and Zhong, 1988).
(2) ‘AND’ Composition
Given a rule with the following format : [A
i
1
AND
A
i
2
AND … AND A
i
K
] → B
i
, we can determine the
overall MF(OMF
i
) based on Eqs. (6) or (7) by
averaging MF
ij
regarding all corresponding pairs of
(A
ij,
A
ij
′), where i denotes the i
th
rule and j = 1,2,…,k.
In this case, Eq. (8) is changed into as follows :
OMF
i
=avg {avg MF
ij
(A
ij,
A
ij
′)} where each MF
ij
(A
ij,
A
ij
′) is derived from Eq.(6) or (7), respectively, and a
group of observations has the same form [A
i
1
′ AND
A
i
2
′ AND… AND A
i
K
′]. (11)
Example 2. We consider the i
th
rule with ‘AND’
connectives in the form ‘IF X
1
is A
i
1
AND X
2
is A
i2
AND X
3
is A
i3
THEN Y is B’. For simplicity, let A
i
1
=(1,2,3), A
i
2
=(3,4,5,6), A
i
3
=(6,7,8), and A
i
1
′=(2,3,4),
A
i
2
′=(4,5,6,7), A
i
3
′=(7,8,9), respectively, (i.e., k = 3)
then the OMF
i
is obtained by using Eqs.(6),(7), (11).
OMF
i
= (
∑
=
3
1j
avg (MF
ij
))/3
={[(1+((2-1)/(4-1)))+(1+((3-2)/(4-1)))+(1+((4-3)/(4-
1)))]/3+[(1+((4-3)/(7-3)))+(1+((5-4)/(7-3)))+(1+((6-
5)/(7-3)))+(1+((7-6)/(7-3)))]/4+[(1+((7-6)/(9-
6)))+(1+((8-7)/(9-6)))+(1+((9-8)/(9-6)))]/3}/3
= {(1+(1/3))+(1+(1/4))+(1+(1/3))}/3 = 1.3.
The OMF
i
(i.e., 1.3) will be used in the consequent
deducing phase as follows :
μ A
i1
A
i1
′A
i2
A
i2
′A
i3
A
i3
′ μ B
i
B
i
′
1 1
1 2 3 4 5 6 7 8 9
X 1 1.3 2 2.6 3 3.9 Y
Figure 3: An example of ‘AND’ connectives.
4 COMPARISONS
Some comparisons are in Table 1.
Table 1: Comparisons.
Attributes Existing methods Proposed method
Mem. fn. Ad-hoc SPMF
Method Genreally, CRI Based on SPMF
Formula Complex Simple
Operation Generally, matrix Linear
5 CONCLUSIONS
The proposed method provides an efficient
mechanism for approximate reasoning within linear
time complexity.
REFERENCES
Chang, T. C., Hasegawa, K., Ibbs, C. W., 1991. The
Effects of Membership Function on Fuzzy Reasoning,
Fuzzy Sets and Systems 44, 169-186
Mizumoto, M., 1985. Extended Fuzzy Reasoning, In :
Gupta et al. (Eds.), Approximate Reasoning in Expert
Systems (North-Holland) 71-85
Turksen, I. B., Zhong, Z., 1988. An Approximate
Analogical Reasoning Approach Based on Similarity
Measures, IEEE trans. on SMC 18(6), 1049-1056
Zadeh, L.A., 1973. Outline of a New Approach to the
Analysis of Complex Systems and Decision Processes,
IEEE Trans. on SMC 3, 28-44
Zadeh, L.A.,
1975. The Concept of a Linguistic Variables
and Its Application to Approximate Reasoning I, II, III,
Part I: Inf. Sci. 8, 199-249, Part II: Inf. Sci. 8, 301-357,
Part III: Inf. Sci. 9, 43-80.
Zwick, R. et al. 1987, Measures of Similarity among
Fuzzy Concepts : A Comparative Analysis, Int. J. of
Approximate Reasoning 1, 221-242
Big earning (B)
Deduced
earning
(B′)
ICEIS 2008 - International Conference on Enterprise Information Systems
386