AN OPTIMIZATION PROCEDURE TO RECONSTRUCT THE

AUTOMOBILE INGRESS MOVEMENT

Ait El Menceur M. O., P. Pudlo, F.-X. Lepoutre

LAMIH UMR CNRS 8530, University of Valenciennes, Valenciennes, France

P. Gorce

HANDIBIO-LESP EA 31-62, University of Sud Toulon-Var, La Garde, France

Keywords: Multi objective optimization, Modelling and simulation, Automobile ingress movement reconstruction.

Abstract: To simulate the automobile ingress movement, joint angles are needed. The joint angles are computed from

the experimental data issued from an optoelectronic motion capture system. As these systems are often

corrupted by problems related either to the system or to the experimentation, the computed angles are

biased. Lempereur et al. (2003) proposed an optimization procedure to remedy to this problem. However,

their method gives good results only on the end effectors’ trajectories, while the other bodies’ trajectories

are not considered by their method. That degrades the positions of these parts and causes their eventual

collisions with the vehicle’s parts. On the other hand the corrected angles present some vibrations causing

unrealistic simulation. In this paper we present a multi objective optimization based procedure to correct the

joint articulation angles in automobile ingress movement. Our method minimizes the distance between all

reconstructed trajectories with the real ones at each step of time. Our method follows a compromise between

all trajectories of the model. Our method gives better global results. Correction of the joint angles allows a

realistic simulation.

1 INTRODUCTION

Automobile accessibility is a serious problem for

elderly and/or disabled people that can lead them to

stop driving definitely (Cappelaere et al., 1991). To

avoid losing these customers, who are in a

continuous increasing in the industrialized countries

(Brutel, 2002), car manufactures show their interest

in this population and in its behaviour during the

accessibility movement. The new vehicles tend to be

adapted so that to give less discomfort for drivers.

However, vehicles can not be modified without

considering the driver. Traditionally car

manufactures use physical mock ups to test new

vehicle prototypes. However, this procedure is very

expensive and less reliable (Verriest, 2000). To

remedy to its disadvantages, car manufactures had

the recourse to the using of numerical simulation

(Porter et al., 1993), (Tessier, 2000). HANDIMAN

project goes in this direction and aims to integrate

the accessibility discomfort evaluation in the first

stage of the new vehicle conception for elderly

and/or disabled people (Ait El Menceur et al., 2007).

This evaluation is done on the basis of the

accessibility movement simulation. Simulation

requires modelling of the system to simulate. In our

case the system is the human being.

Modelling requires knowledge of the system.

The knowledge is acquired from the experimentation

on the human being. In HANDIMAN project we

used an optoelectronic motion capture system to

capture the ingress/egress movements of elderly

and/or disabled people (Ait El Menceur et al., 2007).

Even though they are among the most reliable

movement studying systems, the use of

optoelectronic systems encounters some problems

(Cappozzo et al., 1996). These problems are due

either to the system itself or to the experimental

protocol. One of the problems met in the

reconstruction, and caused by the experimental

protocol, is the computation of joint articulation

angles from non rigid bodies (human body) and the

integration of these angles in a rigid body structure

(humanoid model). The resulted angles are biased

and their using in the movement reconstruction

induces false trajectories of the humanoid. These

165

El Menceur M. O. A., Pudlo P., Lepoutre F. and Gorce P. (2008).

AN OPTIMIZATION PROCEDURE TO RECONSTRUCT THE AUTOMOBILE INGRESS MOVEMENT.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 165-168

DOI: 10.5220/0001498001650168

 SciTePress

trajectories can provoke the humanoid’s collision

with the different vehicle’s parts (collision of the

head with the roof, knee with the steering wheel,

penetration of the humanoid inside the seat…).

Lempereur et al. (2003) proposed an

optimization based approach to remedy to this

problem. This procedure minimizes at each step of

time the distance between the measured trajectory

(desired trajectory) of the end effector and the

trajectory of the humanoid reconstructed from the

computation of the joint angles. This procedure

gives good results on the end effortor’s trajectories.

However, as it does not consider other body parts’

trajectories (like knees, ankles) these lasts can have

erroneous trajectories as they can enter in collision

with the vehicle’s parts.

In our study we propose an optimization method

based on a multi objective function that considers

the trajectories of many body parts. Our method

aims to minimize at each step of time the distance

between the measured trajectories and the

trajectories of some body parts (feet, ankles, knees,

hips, trunk, neck and head).

Our paper is organized as follows: Section 2

presents the method. Section 3 will detail our

optimization procedure. The results will be shown in

section 4. The paper is concluded in section 5.

2 METHOD

2.1 Experimentation

The experiments were conducted as part of the

French HANDIMAN (RNTS 2004) project. This

project aims at integrating the ingress/egress

discomfort for elderly and/or disabled persons in

first stages of new vehicle conception for these

populations. This project considers several trials of

ingress and egress movement of 41 test subjects on

four vehicles representative of a large part of

vehicles present in the trade (Ait El Menceur et al.,

2007). In the present study only the ingress trial of

one subject on one vehicle is considered, the other

trials of other subjects are similar. The trial is

performed on a minivan vehicle (see figure 1).

An optoelectronic motion capture system

Vicon® 612 at sampling rate of 60 Hz is used. The

system is equipped with 8 CCD cameras.

Fifty three anatomical markers are set on the

different body segments of the subject to capture the

movements during the different acquisitions (Ait El

Menceur et al., 2007).

The joint angles are computed for each joint. The

ISB recommendation is adopted (Wu et al., 2002).

Figure 1: The stripped vehicle used in the study.

2.2 Humanoid Model

To reconstruct the ingress movement, we propose a

three dimensional model of 20 DOF considering the

two lower limbs and the trunk with the head.

The 20 DOF of the Humanoid model are

partitioned as follows: 3 DOF for each hip, 3 DOF

for the joint linking the two bodies of the trunk (T10

vertebra according to (Lempereur et al., 2005)), 3

DOF for the joint linking the head to the upper

trunk, 2 DOF for each knee and ankle. The

humanoid’s articulations are rotoid. The convention

of Denavit and Hartenberg (Denavit and Hartenberg,

1955) was adopted in the humanoid modeling

process. The humanoid model is represented in

figure 2.

Figure 2: Humanoid model.

3 OPTIMIZATION PROCEDURE

Our method uses a multi objective optimization

procedure. It minimizes the sum of the distances

between all reconstructed trajectories of different

body parts of our humanoid with the measured ones.

The mathematical formulation of our optimization

problem is given by the following expression.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

166

∑∑

−=−

jidi

idi

)q(fXminXXmin (1)

With N is the number of the body parts whose the

positions are to be corrected.

. : is the Euclidian

distance (norm)

with j=1…7 (for the lower limbs

chain) and j=1…6 (for the trunk chain) are the

calculated joint angles.

are parts of the forward

geometric function giving the positions of each body

part.

The final expression of our optimization procedure

is given as follows:

⎪

⎩

⎪

⎨

⎧

<−

ε<−

∑

−

i1ii

iicali

maxiimini

jidi

Vqq.SC

qq.SC

qqq.SC

)q(fXmin

(2)

The first constraint concerns the physiological

angles limitation (Kapandji, 1974).

The second constraint imposes to the optimized

angles to not diverge too much from the calculated

angles.

ε are found after several trial and error tests.

For the lower limbs chains we kept same values of

ε proposed by Lempereur et al. (2003). For the

trunk chain we identified the corresponding

Table 1: Values of

for the trunk chain.

Joints

Joint linking the two parts of the trunk

- Flexion/Extension 19°

- Abduction/Adduction 17°

-Lateral/Medial rotation 13°

Joint linking the head to the upper

trunk

- Flexion/Extension 23°

- Abduction/Adduction 17°

-Lateral/Medial rotation 13°

The third constraint is the constraint of

continuity.

V is the maximum variation allowed

between two successive optimized angles.

The maximum variations of the different joints

depend on the movement and on the population.

Like in (Lempereur et al., 2003) our optimization

procedure is achieved by using the Matlab®

Optimization toolbox which uses the sequential

quadratic program.

4 RESULTS

We have applied the method of Lempereur et al.

(2003) and our method on different kinematic chains

of our model. In general the method of Lempereur et

al. (2003) gives good results on the end effectors

trajectories. However it degrades the positions of

other parts. On the other hand, the angles corrected

by the method of Lempereur et al. (2003) show

many vibrations and these lasts influence negatively

on the reconstruction and rendering it “unrealistic”.

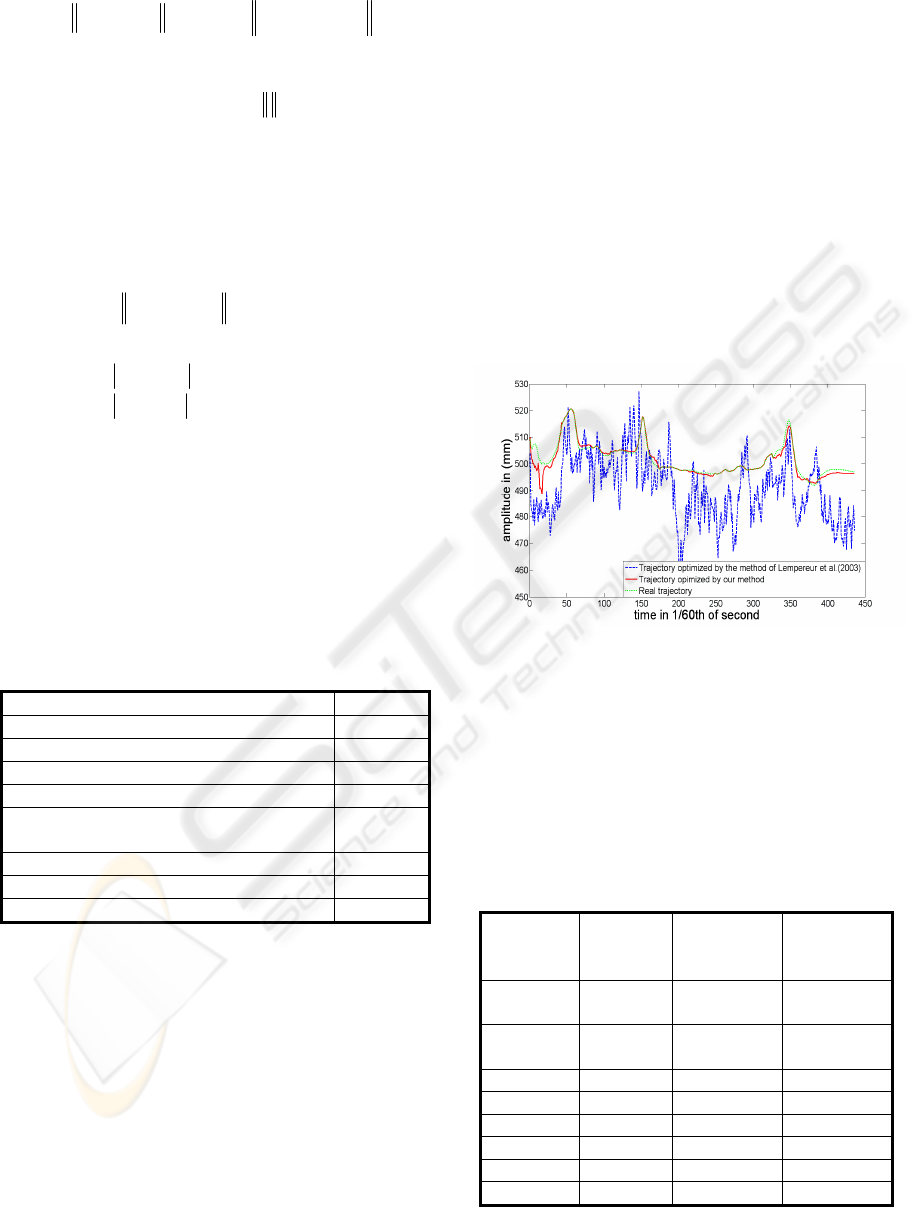
For an illustration purpose we present the

optimization results of the method of Lempereur et

al. (2003) and our method on a bit of the right ankle

trajectory. Our method allows good correction of the

right ankle trajectory. On the other hand this last is

smoothed.

Figure 3: Right ankle different trajectories.

The three dimensional RMS between, respectively,

reconstructed trajectories, trajectories optimized by

Lempereur et al. (2003) method, our method and the

real trajectories are represented in table 2

Table 2: RMS (in mm) between, respectively,

reconstructed trajectories, trajectories optimized by

Lempereur et al. (2003) method, our method and the real

trajectories.

Model

Method of

Lempereur

et al. (2003)

Our method

Right

knee

19.0 19.4 18.5

Right

ankle

19.3

6.4

3.7

Right foot 20.1 0.0 3.3

Left knee 23.5 32.6 25.4

Left ankle 23.3 13.0 5.6

Left foot 24.4 0.3 5.0

C7 4.3 56.8 34.6

Head 69.6 5.7 16.6

AN OPTIMIZATION PROCEDURE TO RECONSTRUCT THE AUTOMOBILE INGRESS MOVEMENT

167

The method of Lempereur et al. (2003) gives good

results on the end effectors’ trajectories which can

even lead to their superposition with the measured

trajectories.

However we can see some degradations on other

body parts trajectories (like knees and ankles) and

that induces to eventual collisions of these parts with

the vehicle’s parts, like collision of the knee with the

steering wheel or penetration of the legs inside the

seat.

5 CONCLUSIONS

We have proposed another optimization method

based on a multi objective function to correct the

joint articulation angles in automobile ingress

movement. Our method minimizes at each step of

time the distances between all humanoid body parts’

trajectories and their real trajectories. We kept same

constraints defined by Lempereur et al. (2003) for

the lower limbs.

Unlike the method of Lempereur et al. (2003),

our method gives good global results on all

trajectories. This is due to the fact that it follows a

good compromise between all trajectories and at

every step of time.

The correction of the joint angles will allow a

realistic simulation.

Our method presents slight degradations of some

body parts’ trajectories. That can be enhanced by

integrating some weighting factors on some

trajectories.

ACKNOWLEDGEMENTS

This research was supported financially by the

European Community, the Délégation Régionale à la

Recherche et à la Technologie, the Ministère de

l'Education Nationale, de la Recherche et de la

Technologie, the Région Nord Pas de Calais and the

Centre National de la Recherche Scientifique. The

authors gratefully acknowledge the support of these

institutions.

The authors would like to thank those at SMPR,

INRETS, and Renault who participated in the

HANDIMAN project.

REFERENCES

Ait El Menceur, M-O., Pudlo, P., Découfour, N.,

Bassement, M., Gillet, C., Chateauroux, E., Gorce, P.,

Lepoutre, F-X., 2007. Towards dynamic studying of

the car ingress/egress movement for elderly and

disabled population. in proceeding with IEEE

HUMAN'07, Human Machine iNteraction Conference,

Timimoun, Algeria, march 12-14

. pp. 350-355.

Brutel C., 2002. La population de la France métropolitaine

en 2050 : un vieillissement inéluctable. Economie et

Statistique, N°355-356, pp 57-71.

Cappelaere, A., Thévenon, A., Delcambre, B., 1991.

Polyarthrite rhumaoïde et conduite automobile. Essais

contrôlés d’un véhicule de série. Ann. Réadaptation

Méd. Phys, 34, pp 239-244.

Cappozzo, A., Catani, F., Leardini, A., Benedetti, M. G.,

Croce, U. D., 1996. Position and orientation in space

of bones during movement : experimental artifacts,

Clinical Biomechanics, Vol. 11, No. 2, pp. 90-100.

Denavit, J., and Hartenberg, R. S., 1955. A kinematic

notation for lower pair mechanism based on matrices,

Journal of Applied Mechanics, Vol. 22, pp. 215-221.

Kapandji, I. A., 1974. Physiologie articulaire, Fascicule II,

Membre inférieur, Librairie Maloine S. A., Paris.

Lempereur, M., Pudlo, P., Gorce, P., Lepoutre, F-X.,

2003b. Optimization approach for the simulation of

car accessibility movement. Proc. of the IEEE

International Conference on Systems Man and

Cybernetics, october 5-8, Washington DC, USA,

octobre, ISBN 0-7803-7953-5.

Lempereur, M., Pudlo, P., Gorce, P., Lepoutre, F-X.,

2005. Mannequin virtuel adapté à la simulation du

mouvement d'entrée-sortie au véhicule automobile.

Journal Européen des Systèmes Automatisés, 38 (7-8),

pp. 959-976.

Porter, J. M., Case, K., Freer, M.T., Bonney, M.,

1993.Computer-Aided Ergonomics Design of

Automobiles. In Automotive Ergonomics, Eds.

Peacock and Karwonski, Taylor & Francis, 43- 78.

ISBN: 0748400052, 1993.

Tessier, Y., 2000. Vers des mannequins numériques

integrés dans la conception de produits . Les modèles

numériques de l'homme pour la conception de

produits, Lyon-Bron.

Verriest, J. P., 2000. Les mannequins numériques dans la

conception de produits. Les modèles numériques de

l'homme pour la conception de produits , Mars 2000,

Institut National de Recherche sur les Transports et

leur Sécurité.

Wu G., Siegler S., Allard P., Kirtley C., Leardini A.,

Rosenbaum D., Whittle M., D'Lima D. D.,

Cristofolini L., Witte H., 2002. ISB recommendation on

definitions of joint coordinate system of various joints

for the reporting of human joint motion--part I: ankle,

hip, and spine. Journal of Biomechanics, 35(4), 543-54.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

168