
IDENTIFICATION OF MULTI-DIMENSIONAL SYSTEM BASED ON
A NOVEL CRITERION
Yue Zhao, Kueiming Lo
School of Software, Tsinghua University, Key Lab for ISS, MOE China, Tsinghua University, Beijing 100084, P. R. China
Wook-Hyun Kwon
School of Electrical Engineering, Seoul National University, Seoul 151-742, Korea
Keywords:
Multi-dimensional system, identification criterion, ARMAX model, recursive algorithm.
Abstract:
Most system recursive identification algorithms are based on the prediction error (PE) criterion. Such a re-
cursive algorithm only considers the present estimation residual error instead of all estimation residuals. It
would result in large estimation error when the signal noise disturbs strongly. In this paper, a new iden-
tification criterion is proposed. It considers both the errors between the actual outputs and the estimation
result and the difference of each estimation error. Under this criterion, a new recursive algorithm MSDCN
(Multi-dimensional System Disturbed by Color Noise) is proposed. For multi-dimensional systems, weight-
ing different values on the estimation errors and the difference of each error, MSDCN could both decrease the
estimation errors and got smooth prediction curves. Several simulation examples are given to illustrate the
method’s anti-disturbance performance.
1 INTRODUCTION
There already have many recursive algorithms for
modeling systems disturbed by white noises (Ander-
sson and Broman 1998, Ljung 1999, Griffith Jr 1999,
Mershed 2000, etc.). The most characteristic fea-
ture of disturbance, however, is that its value is not
known beforehand. A physical system is affected by
many factors such as color noise disturbance and an
un-modeled structure. These types of algorithms en-
counter difficulties when the measurements are dis-
turbed (Kuo 2000, Trump 2001). For multi-discrete
systems disturbed by color noise, current identifica-
tion algorithms cannot give precise estimate results
either (Schoukens 1991, Ljung 1985).
Efficiency modeling depends on the choice
of identification criterion. Combining frequency-
domain method and time-domain method the GPE
criterion was proposed for interference systems (Lo
and Kwon 2002, 2003). Some extended recursive al-
gorithms (ERA) were put forward based on the GPE
criterion. (Lo and Kimura 2003, Lo et al. 2006, and
Lo and Huang 2006) Usually, a GPE criterion con-
tains a weighting matrix, in which there are many pa-
rameters for free choice. When the weighting matrix
is the identity, the ERA becomes the recursive least
squares algorithm (Lo and Kimura 2003). In addition,
the standard Yule-Walker method uses identity ma-
trix as weighting matrix. It may have poor accuracy,
and increasing the dimension of the weighting ma-
trix may well degrade the accuracy (Stoica, Friedlan-
der and Soderstrom 1987). Stoica and Jansson (2001)
proposed another method which derived the optimal
weight in a simple way and guaranteed the optimal
weighting matrix to be consistent and non-negative
definite, while still the choice of weighing matrix is
hard. Furthermore, for all the above raised implemen-
tations, a positive definite weighting matrix must be
weighted out in order to get a reliable estimate. The
optimal weight in general depends on unknown quan-
tities and hence must be itself estimated before its use
become possible.
Considering both the prediction errors and the dif-
ference of each error, performancecriterion in this pa-
per applies different weights. One part is the errors
between the actual outputs and the other is the esti-
mation result and the difference of each estimation er-
ror. Further, this paper develops a recursive weighting
matrix for fast calculation in recursive algorithms. In
this matrix, the values of each element depends on the
143
Zhao Y., Lo K. and Kwon W. (2008).
IDENTIFICATION OF MULTI-DIMENSIONAL SYSTEM BASED ON A NOVEL CRITERION.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 143-148
DOI: 10.5220/0001492001430148
Copyright
c
SciTePress

weights of the performance function. Based on this
new performance function, a new recursive algorithm
for multi-system identification, MSDCN, is proposed.
MSDCN algorithm is new not only because it is
based on a new performance function, but also be-
cause it is based on a new concept of estimating the
noise part separately. Its two-step estimation feature
also make it a novel method. The MSDCN algorithm
has good anti-disturbance. For multi-dimensional
system, using the novel criterion to do the complex
estimation in each dimension of parameters, MSDCN
can give more precise results than current algorithms
do.
In the second part of this paper, the extended re-
cursivealgorithm for multi-dimensionalsystems is in-
troduced; The third part proposes a novel identifica-
tion criterion; In the fourth part a recursive algorithm
for multi-dimensional system, MSDCN, is proposed;
An analysis of the performance of new criterion and
new algorithm is given in the fifth section, and then
its simulation results are compared with other algo-
rithms.
2 EXTENDED RECURSIVE
ALGORITHM FOR
MULTI-DIMENSIONAL
SYSTEM
Consider system:
A(q)y(t) = B(q)u(t) + w(t) (1)
where, y(t) and w(t) are p-dimensional vectors, u(t)
is m-dimensional vector. y(t), u(t), and w(t) are sys-
tem output, input, and noise respectively. A(q), B(q)
are the backward operator q
−1
polynomial expression
A(q) = I +
n
a
∑
k=1
A
k
q
−k
, B(q) =
n
b
∑
k=1
B
k
q
−k
.
Denote:
θ = (A
1
, A
2
, ·· · , A
n
a
, B
1
, B
2
, ·· · , B
n
b
)
T
ϕ
t
= (−y
T
(t − 1), ··· , −y
T
(t − n
a
),
u
T
(t − 1), ·· · , u
T
(t − n
b
))
T
where θ ∈ R
(n
a
·p+n
b
·m)×p
is a matrix formed by the
system part parameters. ϕ
t
∈ R
n
a
·p+n
b
·m
is a regres-
sion vector. Then (1) is rewritten as
y(t) = θ
T
ϕ
t
+ w(t) (2)
Denote ε
t
be the prediction error of system output
y(t):
ε
t
= y(t) − θ
T
ϕ
t
, (3)
Then the identification criterion can be expressed
as:
J(N) = tr([ε
1
, ε
2
, ··· , ε
N
]
T
Q(N)[ε
1
, ε
2
, ··· , ε
N
]) (4)
where trA represents the trace of matrix A. The
weighting matrix Q(N) ∈ R
N×N
is a symmetrical pos-
itive definite matrix and expressed as:
Q(N) =
Q(N − 1) α(N)
α(N)
T
q
N
, t = 1, 2, ··· , N
where α(N) ∈ R
N−1
. Denote:
Φ(N) = (ϕ
1
, ϕ
2
, ··· , ϕ
N
)
T
Y(N) = (y
1
, y
2
, ··· , y
N
)
T
Then the identification criterion (4) can be expressed
as:
J(N) = tr([Y(N) − Φ(N)θ]
T
Q(N)[Y(N) − Φ(N)θ]
(5)
Since
J(N) = tr(Y
T
(N)Q(N)Y(N)) −tr(θ
T
Φ
T
(N)Q(N)Y(N))
−tr(Y
T
(N)Q(N)Φ(N)θ) + tr(θ
T
Φ
T
(N)Q(N)Φ(N)θ)
The gradient of J(N) is:
∂J(N)
∂θ
=
∂
∂θ
[tr(Y
T
(N)Q(N)Y(N))
−tr(θ
T
Φ
T
(N)Q(N)Y(N))
−tr(Y
T
(N)Q(N)Φ(N)θ)
+tr(θ
T
Φ
T
(N)Q(N)Φ(N)θ(N))]
=
∂
∂θ
[tr(Y
T
(N)Q(N)Y(N))]−
∂
∂θ
[tr(θ
T
Φ
T
(N)Q(N)Y(N))]
−
∂
∂θ
[tr(Y
T
(N)Q(N)Φ(N)θ)]
+
∂
∂θ
[tr(θ
T
Φ
T
(N)Q(N)Φ(N)θ(N))]
= −(Y
T
(N)Q(N)Φ(N))
T
− Φ
T
(N)Q(N)Y(N)+
(Φ
T
(N)Q(N)Φ(N) + Φ
T
(N)Q(N)
T
Φ(N))θ(N)
and
∂J
2
(N)
∂θ
2
= Φ
T
(N)Q(N)
T
Φ(N)
where Q(N) = Q
T
(N) and
∂J
2
(N)
∂θ
2
is positive and def-
inite. Let
∂J(N)
∂θ
= 0
which minimizes J(N) and yields:
θ(N) = [Φ(N)
T
Q(N)Φ(N)]
−1
Φ(N)
T
Q(N)Y(N)
(6)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
144

t = 1, 2, · ·· Then at time t, denote:
P
t
= Φ
T
t
Q
t
Φ
t
a
t
= 1+ ϕ
T
t
P
−1
t−1
Φ
T
t−1
α
t
σ
t
= q
t
− α
T
t
Φ
t−1
P
−1
t−1
Φ
T
t−1
α
t
b
t
= a
t
+ a
−1
t
σ
t
ϕ
T
t
P
−1
t−1
ϕ
t
Then we can get:
Theorem 1
P
−1
t
= P
−1
t−1
− b
t
P
−1
t−1
(ϕ
t
β
T
t
Φ
t−1
+ Φ
T
t−1
β
t
ϕ
T
t
)P
−1
t−1
+
1
a
t
b
t
P
−1
t−1
(ϕ
T
t
P
−1
t−1
ϕ
t
Φ
T
t−1
β
t
β
T
t
Φ
t−1
− σ
t
ϕ
t
ϕ
T
t
)P
−1
t−1
θ
t
= θ
t−1
+
1
a
t
b
t
P
−1
t
(β
t
Φ
T
t
β
t
+ σ
t
ϕ
t
)(y
t
− θ
T
t−1
ϕ
t
)
+
1
a
t
b
t
P
−1
t−1
(β
t
ϕ
t
− ϕ
T
t
P
−1
t−1
ϕ
T
t−1
β
t
)β
T
t
(Y
t−1
− Φ
t−1
θ
t−1
)
As Extended Recursive Algorithm for multi-
dimensional system.
3 IDENTIFICATION CRITERION
New identification criterion is:
J(N) = λ
N
∑
t=1
k ε
t
k
2
+µ
N−1
∑
t=1
k ε
t+1
− ε
t
k
2
(7)
where ε
t
represents the estimation errors at time t, in
multi-dimensional system, ε
t
is p-dimensional vector,
which dimension is the same as the output y(t).
λ represents the weight on the estimation errors
µ represents the weight on the difference between
each estimation error.
Transforming equation (7), we can get
J(N) =
N
∑
t=1
(λε
T
t
ε
t
) +
N−1
∑
t=1
µ(ε
t+1
− ε
t
)
T
(ε
t+1
− ε
t
))
=
N
∑
t=1
tr(λε
t
ε
T
t
) +
N−1
∑
t=1
µtr(ε
t+1
− ε
t
)(ε
t+1
− ε
t
)
T
= tr
(λ+ 2µ)
N
∑
t=1
ε
t
ε
T
t
− µ
N−1
∑
t=1
ε
t+1
ε
T
t
− µ
N−1
∑
t=1
ε
t
ε
T
t+1
)
Assume E(N) = (ε
1
, ε
2
, ··· , ε
N
)
T
∈ N × p
and
Q(N) =
q
11
q
12
··· q
1N
q
21
q
22
··· q
2N
.
.
.
.
.
.
.
.
.
.
.
.
q
t1
q
t2
··· q
NN
∈ N × N,
in which,
q
i,i
= λ+ 2µ
q
i+1,i
= −µ i = 1, 2, ··· , N.
q
i,i+1
= −µ
Then equivalent with equation (3), we can get
J(N) = trE(N)
T
Q(N)E(N) (8)
as the new expression for the performance criterion.
Thus at time t, the weighting matrix Q
t
can be ex-
pressed in this recursive form:
Q
t
=
Q
t−1
β
t
β
T
t
p
t
, t = 1, 2, · ·· , N
in which, β
t
= [0, 0, · ·· , −µ] ∈ R
t−1
and p
t
= λ+ 2µ.
4 RECURSIVE ALGORITHM
FOR MULTI-DIMENSIONAL
SYSTEM
Consider the ARMAX model
A(q)y(t) = B(q)u(t) +C(q)w(t) (9)
where, y(t) and w(t) are p-dimensional vectors, u(t)
is m-dimensional vector. y(t), u(t), and w(t) are sys-
tem output, input, and color noise respectively. A(q),
B(q), C(q)is the backward operator q
−1
polynomial
expression
A(q) = I +
n
a
∑
k=1
A
k
q
−k
, B(q) =
n
b
∑
k=1
B
k
q
−k
,
C(q) = I +
n
c
∑
k=1
C
k
q
−k
.
where A
k
, C
k
∈ p × p, and B
k
∈ p× m. Denote:
θ = (A
1
, A
2
, ··· , A
n
a
, B
1
, B
2
, ··· , B
n
b
)
T
,
ϕ
t
= (−y
T
(t − 1), · ·· , −y
T
(t − n
a
), u
T
(t − 1), · ·· , u
T
(t − n
b
))
T
,
ρ = (C
1
, C
2
, ··· , C
n
c
)
T
,
φ
t
= (w(t − 1), w(t − 2), ··· , w(t − n
c
))
T
.
in which θ ∈ R
[n
a
·p+n
b
·m]×p
is the matrix formed by
the system part parameters; and ρ ∈ R
[n
c
·p]×p
is the
matrix formed by the system’s noise part parameters.
Here we introduce a two-step algorithm to do the
estimation for system (9).
Step 1: Transform (9) into:
y(t) − ρ
T
t−1
φ
t
= θ
T
t
ϕ
t
+ w(t) (10)
IDENTIFICATION OF MULTI-DIMENSIONAL SYSTEM BASED ON A NOVEL CRITERION
145

Estimate the system parameters θfor system (10). For
the identification of the parameters of system θ, use
the following measurements:
J(t) = tr(λ
N
∑
t=1
k ε
t
k
2
+µ
N−1
∑
t=1
k ε
t+1
− ε
t
k
2
). (11)
Step 2: Transform (10) into:
y(t) − θ
T
t
ϕ
t
= ρ
T
t
φ
t
+ w(t). (12)
Estimate the parameter ρ of filter C(q) of system (9).
Denote
Φ
t
= (ϕ
1
, ϕ
2
, ··· , ϕ
t
)
T
, Y
t
= (y
1
, y
2
, ··· , y
t
)
T
,
g
t
= y
t
− ρ
T
t−1
φ
t
, G
t
= (g
1
, g
2
, ··· , g
t
)
T
And according to equation (8), the novel criterion J(t)
can be expressed as:
J(t) = trE(t)
T
Q
t
E(t)
= tr[ε
1
, ε
2
, ··· , ε
t
]
T
Q
t
[ε
1
, ε
2
, ··· , ε
t
]
= tr[G
t
− Φ
t
θ]
T
Q
t
[G
t
− Φ
t
θ]
If Φ
T
t
Q
t
Φ
t
is not singularthen minimize J
t
to get the
system’s parameter vector θ
t
’s optimal solution:
θ
t
= [Φ
T
t
Q
t
Φ
t
]
−1
Φ
T
t
Q
t
G
t
, t = 1, 2, ··· , N. (13)
Similar with Extended Recursive Algorithm, we
can get MSDCN algorithm for ARMAX model (9):
θ
M
(t) = θ
M
(t − 1)
+
1
a
t
b
t
P
−1
t
(β
t
Φ
T
t
β
t
+ σ
t
ϕ
t
)(y
t
− ρ
M
(t − 1)
T
φ
t
− θ
M
(t − 1)
T
ϕ
t
)
+
1
a
t
b
t
P
−1
t−1
(β
t
ϕ
t
− ϕ
T
t
P
−1
t−1
ϕ
T
t−1
β
t
)β
T
t
(G
t−1
− Φ
t−1
θ
M
(t − 1))
P
−1
t
= P
−1
t−1
− b
t
P
−1
t−1
(ϕ
t
β
T
t
Φ
t−1
+ Φ
T
t−1
β
t
ϕ
T
t
)P
−1
t−1
+
1
a
t
b
t
P
−1
t−1
(ϕ
T
t
P
−1
t−1
ϕ
t
Φ
T
t−1
β
t
β
T
t
Φ
t−1
− σ
t
ϕ
t
ϕ
T
t
)P
−1
t−1
ρ
M
(t) = ρ
M
(t − 1) +
R
−1
t−1
φ
t
1+ φ
T
t
R
t−1
φ
t
(y
t
− θ
M
(t)
T
ϕ
t
− ρ
M
(t − 1)
T
φ
t
)
R
t
= R
t−1
+ φ
t
φ
T
t
bw(t) = y(t) − ρ
M
(t)
T
φ
t
− θ
M
(t)
T
ϕ
t
(14)
in which,
(
p
t
= λ+ 2µ
β
t
= [0, 0, · ·· , −µ] ∈ R
t−1
Initially, θ and ρ can be zero matrix; R
0
, P
0
to-
gether constitute the identity matrix.
5 SIMULATIONS
All the simulations were conducted in the same
computation environment. The main criterions of the
computer were: CPU 1.66GHz, RAM 1G bytes and
with Windows XP OS.
Experiment. A Black-box model is as follows:
y(t) =
B
1
q
−1
I + A
1
q
−1
u(t) +
I +C
1
q
−1
I + A
1
q
−1
w(t)
The real parameters of the system were:
A
1
=
0.325 −1
0.5 −1.1
,
B
1
=
1.9 3.7
−0.4 −0.8
,
C
1
=
−0.7 −0.1
0.8 0.9
.
The color noise sequence {w(t)}
N
1
was a two di-
mensional vector, of which each dimension was com-
posed of different sawtooth wave and random num-
ber generator with variance 2 and the input signal
u(t) = [1 2], each dimension of which was gener-
ated by a square generator. The experiment was con-
ducted using the LS method and the algorithm MS-
DCN method with the sample number N = 1000. The
results are shown in Figures 1,2,3,4,5,6 and the statis-
tics are as follows:
(1)Least-Squares method
The system statistics results are:
θ =
0.2889 0.0361
−0.9823 −0.0177
0.3855 0.1145
−1.2366 0.1366
1.7990 0.1010
3.5981 0.1019
−0.1692 −0.2308
−0.3384 −0.4616
−0.7499 0.0499
0.0907 −0.1907
0.9270 −0.1270
0.8506 0.0494
.
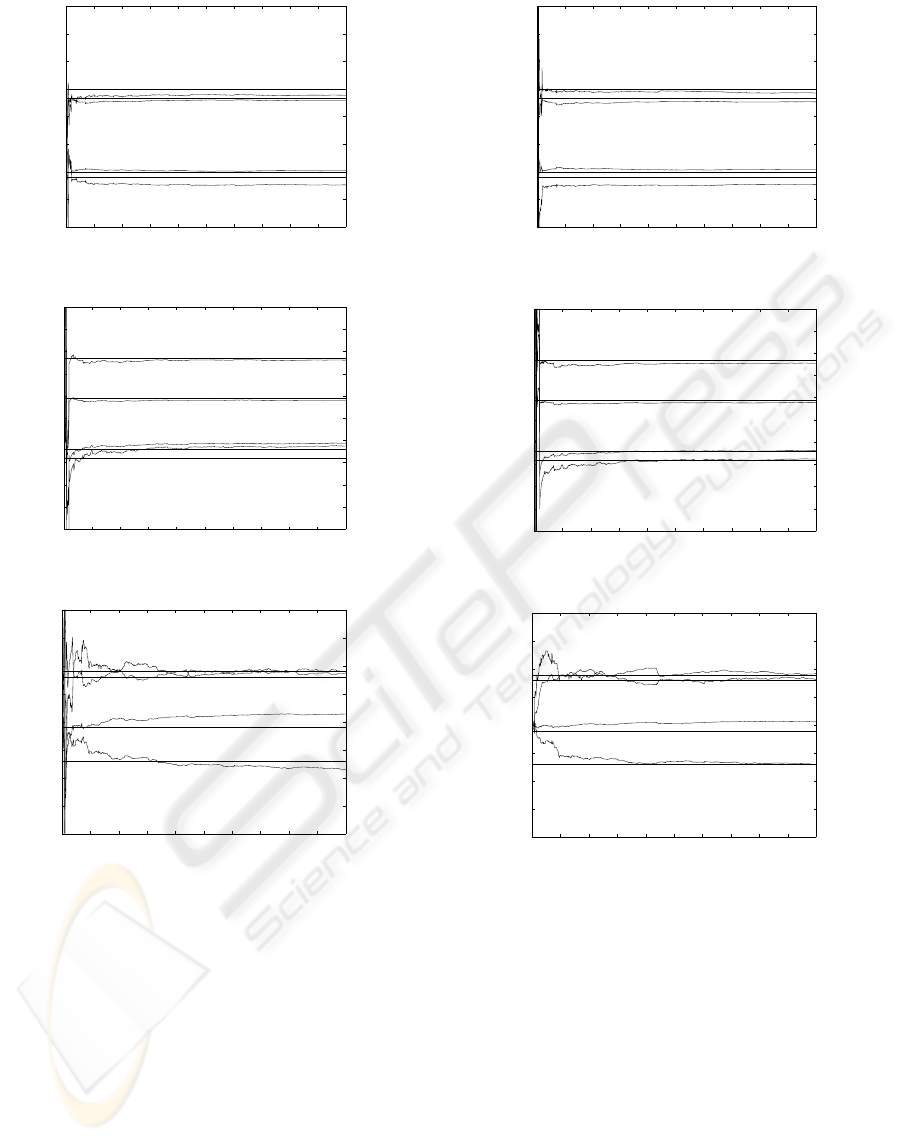
The simulation results are shown in Figure 1, 2
and 3.
(2)MSDCN method
if we choose λ = 0.8andµ = 0.2,
then according to (7), β
t
= [0, ··· , −0.2, −0.2] and
p
t
= 1.2.
Then the system statistics results are:
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
146
0 100 200 300 400 500 600 700 800 900 1000
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
0.325
−1.1
Figure 1: Estimation results of parameter A under ELS.
0 100 200 300 400 500 600 700 800 900 1000
−4
−3
−2
−1
0
1
2
3
4
5
6
3.7
1.9
−0.4
−0.8
Figure 2: Estimation results of parameter B under ELS.
0 100 200 300 400 500 600 700 800 900 1000
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
−0.1
−0.7
0.8
0.9
Figure 3: Estimation results of parameter C under ELS.
θ =
0.2620 0.0630
−0.9602 −0.0398
0.4448 0.0552
−1.2425 0.1425
1.7595 0.1405
3.5189 0.1811
−0.4267 0.0267
−0.8534 0.0534
−0.6499 −0.0501
0.0409 −0.1409
0.8232 −0.0232
0.9362 −0.0362
The simulation results are shown in Figure 4, 5
and 6.
0 100 200 300 400 500 600 700 800 900 1000
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
0.325
−1.1
Figure 4: Estimation results of parameter A under MSDCN.
0 100 200 300 400 500 600 700 800 900 1000
−4
−3
−2
−1
0
1
2
3
4
5
6
3.7
1.9
−0.4
−0.8
Figure 5: Estimation results of parameter B under MSDCN.
0 100 200 300 400 500 600 700 800 900 1000
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
0.9
0.8
−0.1
−0.7
Figure 6: Estimation results of parameter C under MSDCN.
Through a comparison of the estimation results
of ELS and MSDCN, we can see that the new
performance function has proved to be efficient for
the multi-dimensional systems. For the example
given above, we weight 0.8 on the estimation errors
and 0.2 on the difference between each estimation
error, which means we want the estimation curves
close to the actual values more than make the curves
smooth. The weighting matrix is definite after β
t
and
p
t
are fixed by λ and µ. Weighting different on λ and
µ will result in different estimation results. Those
figures show that MSDCN has both decreased the
estimation errors and got smooth prediction curves.
IDENTIFICATION OF MULTI-DIMENSIONAL SYSTEM BASED ON A NOVEL CRITERION
147

6 CONCLUSIONS
This paper proposes a new identification criterion for
multi-dimensional system disturbed by color noise,
and further develops a recursive algorithm, MSDCN,
based on it. Weighting both on the prediction er-
rors and the difference of each prediction error, the
identification criterion makes the weighting matrix
definite in calculation. Based on this performance
criterion, MSDCN is developed using a two-step
method to estimate both the system parameters and
the noise part. The MSDCN algorithm has high anti-
disturbance performance in the prediction of multi-
dimensional systems disturbed by color noise. It both
decreased the estimation errors and got smooth pre-
diction curves. The performance of the MSDCN al-
gorithm was demonstrated by simulations.
ACKNOWLEDGEMENTS
This work is supported by the Funds NSFC60672110,
NSFC60474026,and the JSPS Foundation.
REFERENCES
Andersson, A. and Broman, H. (1998), A second-order re-
cursive algorithm with applications to adaptive filter-
ing and subspace tracking. IEEE Trans. Signal Pro-
cessing, vol. 46, pp. 1720C1725, June.
Griffith Jr, D. W. and Arce, G. R. (1999), A partially decou-
pled RLS algorithm for volterra filters. IEEE Trans.
Signal Processing, vol. 47, pp. 579C582, Feb.
Kuo, C. J. , Jr, R. D. , Lin, C. Y. and Tsai, Y. C. (2000), Set-
theoretic estimation based on a priori knowledge of
the noise distribution. IEEE Trans. Signal Processing,
vol. 48, pp. 2150C2156, July.
Lo, K. M. , et al. (2006), Empirical frequency-domain
optimal parameter estimate for Black-box processes.
IEEE Transactions on Circuits and Systems-I: Regu-
lar Papers, vol.53, No.2, 419-430.
Lo, K. M. , Kwon, W. H. (2003), New identification ap-
proaches for disturbed models. Automatica.vol.39,
No.9, 1627-1634.
Lo, K. M. , Kimura, H. (2003), Recursive Estimation Meth-
ods for Discrete Systems. IEEE Trans. On Circruits
and Systems.vol.49, NO.6, No.6, 439-446.
Ljung, L. (1985), On the estimation of transfer function.
Automaticavol. 21, 677-696.
Ljung, L. (1999), System Identification: Theory for the
User. Upper Saddle River,NJ: Prentice-Hall, 1999.
Mershed, R. and Sayed, A. J. (2000), Order-recursive RLS
Laguerre adaptive filtering. IEEE Trans. Signal Pro-
cessing, vol. 48, pp. 3000C3010, July.
Stoica, P., Friedlander, B.and Soderstrom, T.(1987) Op-
timal Intrumental Variable Multistep Algorithms for
Estimation of the AR Parameters of an ARMA Pro-
cess, Int. J. Control 45(1987), 2083-2107.
Stoica, P. and Jansson, M.(2001) Estimating Optimal
Weights for Instrumental Variable Methods. Digital
Signal Processing - A Review Journal vol. 11, no. 3,
pp. 252-268, Jul. 2001.
Trump, T. (2001), Maximum likelihood trend estimation
in exponential noise. IEEE Trans. Signal Processing,
vol. 49, pp. 2087C2095, Sept.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
148
