
LOCALIZATION IN AN INTERACTIVE SYSTEM
Juan J. Jiménez, Francisco R. Feito and Rafael J. Segura
University of Jaen, Campus Las Lagunillas s/n, Jaen, Spain
Keywords: Interaction, localization, collision detection, virtual reality, real time, tetra-tree.
Abstract: The localization of the nearest parts of an object to a device is usually solved by means of a proximity
measurement of each one of the features that form this object to the device. In order to perform this
efficiently, hierarchical decompositions of the space or of the object are used, so that the features of objects
are classified into several types of cells, usually rectangular. In this paper we propose a solution based on
the classification of a set of points located on the device in a spatial decomposition named tetra-tree. Using
this type of spatial decomposition gives us several qualitative properties that allow us a more realistic and
intuitive visual interaction. In order to show these properties we have compared an interaction system based
on tetra-trees to one based on octrees.
1 INTRODUCTION
In several virtual reality systems (Burdea and
Coiffet, 2003) it is usual for the user to move a
device through the scene, so that the user tries to
interact with the different objects that form the
virtual world. In order to do this precisely, the
system must provide the user with feedback in the
form of visual information (Sherman and Craig,
2003). This usually consists of such parts of the
object that are interacting or are going to interact.
This information could consist of the parts nearest to
the device, so that the system gives information to
the user about the interactive object features, even
before touching them. In this case the interaction
does not produce undesired effects, such as collision
response (deformation, etc.) without previous
knowledge of the area of interest.
In order to solve this problem, image-based
techniques could be used (Schneider and Klein,
2007), but these tend to be less precise. In addition,
interaction possibilities are limited due to the type of
feedback obtained.
In the case of object-based techniques, it is
habitual to use a proximity measurement from the
device to the objects, aided by a spatial
decomposition or by a bounding volume hierarchy
(Ericson, 2005), in order to classify the triangles of
the object and thereby reduce the number of features
to consider. Grids (Samet, 1990) and octrees (Ayala
et. al, 1985) are usually used for this aim, as well as
AABB-Trees (van den Bergen, 2004), OBB-Trees
(Gottschalk et. al, 1996) and Sphere-Trees
(Hubbard, 1996), among others.
Using these types of decompositions and
bounding volume hierarchies, although they are
appropriate when the device is near the object, do
not give suitable information when the device is at a
greater distance. In addition they present problems
of amplitude and continuity in relation to the
triangles displayed when the device moves.
Due to the aforementioned discussion, we will
use a spatial decomposition based on tetra-cones,
called tetra-tree (Jimenez et. al, 2006). This data
structure is constructed for each object of the scene
in pre-processing time. Simultaneously, the triangles
of the objects are classified in the tetra-cones that
from the tetra-tree of each object.
In interaction time, a set of selected and
significant points from the device are classified in
the tetra-trees of the objects, allowing us in this way
to display the triangles classified in the tetra-cones
in which these points are located. This system will
allow us to perform some operations requested by
the user, i.e. to change the amplitude (triangles to
display) by modifying the depth in the tetra-tree.
In addition this system provides us with a smooth
transition of the displayed triangles when the device
moves, in order to display (or not) the nearest
triangles. All these properties allow us to obtain a
more intuitive system and with better qualitative
properties with regard to other systems.
435
J. Jiménez J., R. Feito F. and J. Segura R. (2008).
LOCALIZATION IN AN INTERACTIVE SYSTEM.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 435-438
DOI: 10.5220/0001093604350438
Copyright
c
SciTePress

This paper is organized in the following way: In
the next section the use of the interaction system is
described. After that, a study of some qualitative
properties is carried out, compared with the use of a
octree. Afterwards, the time obtained by the system
is studied for different types of objects. Finally, the
main contributions of this method and the future
work to be undertaken are summarized.
2 INTERACTION SYSTEM
The virtual environment we are dealing with is
composed of objects modelled by means of triangle
meshes. The device can be a hand or a pointing
device (Figure 1). In these cases, several points have
been distributed strategically by the device, so that
they will allow us to determine the triangles of the
objects that are in relative proximity to the device.
Figure 1: Devices used and control points.
Points have been placed mainly in parts of the
device in which presumably the first contact in case
of collision will take place. We have named these
control points. For example, in the hand device
control points are necessary on the endpoint of the
fingers, on the joints and on the palm. In the
pointing device these are necessary on the part
where presumably the interaction will take place, as
well as points uniformly distributed by the device. In
the case of the pencil, only one control point has
been used on its end.
In this system we will consider two possible
situations in which we wish to obtain the triangles
related to the interaction., drawing the triangles
referred to in each case:
Expected triangles: Triangles of the object in
relative proximity to the device in movement,
without collision with the object (Figure 2.a).
Collision triangles: Triangles of the object that
the device interacts with (Figure 2.b). In this case it
is necessary to call the collision detection module in
case a suitable response is needed.
Figure 2: a) Expected triangles for interaction. b) Collision
triangles.
The collision detection module first checks the
collision of the control points with the object. In
order to do this it verifies the inclusion of these
points in each one of the triangles classified in the
tetra-cone in which the control point is included,
using the inclusion algorithm developed by (Feito et.
al, 1997), and optimized for this case, considering
the temporal and geometric coherence. Only if none
of the control points are inside the object is an
intersection test between triangles of the object and
the device required.
This system takes advantage of the temporal and
geometric coherence of the environment when the
device moves through the scene, first verifying the
inclusion of the control points in the tetra-cones in
which they were located in the previous frame, in
order not to classify these points through the
different levels of the tetra-tree. Thanks to the
coherence, most of the time the control points are in
the same tetra-cone as in the previous frame.
3 PROPERTIES OF THE
INTERACTIVE SYSTEM
The use of tetra-trees (Jimenez et. al, 2006) provides
a set of advantages with regard to other types of
spatial decompositions based on rectangular cells,
like octrees and grids, or bounding volume
hierarchies, like AABB-Trees and OBB-Trees.
These advantages are given mainly by an interactive
visualization of the triangles that take part or are
close to taking part in an interaction or manipulation
of the objects, this visualization being more intuitive
and offering a better sensation to the user with
regard to other types of decompositions.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
436
3.1 Obtaining the Triangles Related to
the Interaction
The use of tetra-trees allows us to obtain the
triangles related to an interaction, independently of
the distance of the device from the object. When the
distance increases, the number of expected triangles
diminishes, because the set of tetra-cones in which
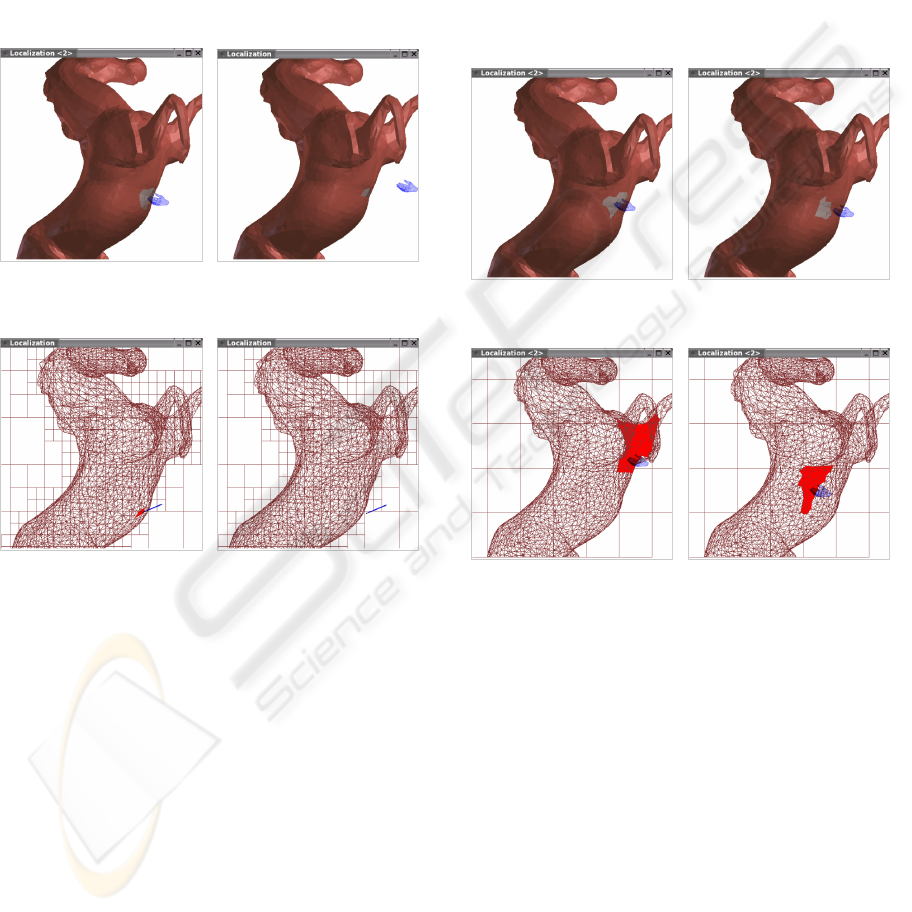
the control points are is smaller (Figure 3).
However, the closer the device approaches, the more
related the triangles are to the future interaction.
Figure 3: When the distance increases, the number of
expected triangles diminishes.
Figure 4: In an octree there are situations in which we do
not obtain a set of triangles related to the interaction.
Nevertheless, in an octree there are cases in
which the control points are not classified (because
they are outside the bounding box) or are classified
in empty cells (without triangles, Figure 4), the
reason why this classification does not obtain a
satisfactory set of triangles related to the interaction.
This set has worse distribution in an octree, because
the cells fits deficiently to the geometry of the
object, presenting worse visual appearance.
3.2 Smooth Transition between Cells
When the device moves a change in the set of cells
in which this object has been classified takes place.
In order to obtain a more agreeable visual sensation
a smooth transition is necessary between the
triangles classified in both sets of cells, that is to say
that the set of triangles shown between two frames
has certain overlapping triangles, and that they
contain a similar number of triangles.
When using tetra-trees the transition between
cells (tetra-cones) is smooth, and discontinuity in the
set of triangles between consecutive frames is not
noticed (Figure 5). However, when using rectangular
cells as in the case of octrees, we noticed an abrupt
transition in the set of triangles between two
consecutive frames (Figure 6), either because of the
difference in the size of the cells, or because the cell
is empty (it does not contain triangles).
Figure 5: Smooth transition between cells in a tetra-tree.
Figure 6: Transition between cells in an octree.
3.3 Smooth Transition between Levels
In any given moment, the user may be interested in
modifying the level of detail for the interaction, and
displaying a greater or lesser number of triangles. In
order to do this it is necessary to increase or
diminish the level reached in the tree.
A tetra-tree has a greater set of levels than an
octree for an equal number of space subdivisions;
therefore it provides a smoother transition between
detail levels. On the other hand, in an octree this
change in the level of detail is more abrupt, and due
to the fact that the cells' form is worse adapted to the
geometry of the object, the set of triangles obtained
may be quite far from the device.
LOCALIZATION IN AN INTERACTIVE SYSTEM
437

4 TIMES STUDY
The system was implemented in C++ using gcc and
OpenGL for visualization. We used an Intel Pentium
IV-1.6 GHz processor with 1 MB in a Linux O.S..
We measured the number of frames per second
in the worst case (when collision with the objects
takes place) obtained by the interaction system for
each one of the objects of Figure 7 and the devices
of Figure 1. In this study we have included the time
consumed in obtaining the related triangles and the
collision detection time. The time needed for
visualization has not been included.
In this system the user moves both, the device
and objects freely throughout the scene. In Figure 8
we can see these times providing a real time
interaction system.
Figure 7: Objects used (f=faces): cylinder (60 f), cat (760
f), teapot (993 f), horse (7,172 f), venus (11,241 f), golf-
ball (16,205 f), dragon (201,031 f).
1
10
100
1.000
10.000
100.000
1.000.000
10.000.000
frames/sec.
hand ball-pen pen
hand
256.004 28.273 18.700 6.515 4.251 1.517 748
ball-pen
682.667 90.474 69.456 29.967 18.219 12.135 7.278
pen
1.600.036 904.737 801.411 449.498 404.875 384.285 309.049
cylinder cat teapot horse venus golfball dragon
Figure 8: Interaction times (frames/sec. in the worst case,
with logarithmic scale).
5 CONCLUSIONS
In this paper we have used a data structure for space
decomposition, especially appropriate for the
location of the parts of an object for interaction. This
data structure presents several advantages with
regard to other space decompositions and hierarchies
of bounding volumes based on rectangular cells,
mainly regarding the obtaining of the related
triangles, the accurate level of detail, and with a
better visual appearance and comfort in the
interaction.
The system obtained is able to perform an object
interaction in real time, including collision detection
with devices, by using certain control points on the
device in order to obtain the triangles related to the
interaction.
ACKNOWLEDGEMENTS
This work has been partially funded by the Ministry
of Science and Technology of Spain and the
European Union by means of the ERDF funds, under
the research projects TIN2004-06326-C03-03 and
TIN2007-67474-C03-03, and by the Consejería de
Innovacion, Ciencia y Empresa of the Junta de
Andalucía under the research project P06-TIC-
01403.
REFERENCES
Ayala, D., Brunet, P., Juan, R., Navazo, I., 1985. Object
representation by means of nonminimal division
quadtrees and octrees. ACM Trans. on Graphics 4, 1.
Burdea, G.C., Coiffet, P., 2003. Virtual Reality
Technology. Wiley-IEEE.
Ericson, C., 2005. Real-Time Collision Detection. Morgan
Kaufmann publishers, Elsevier.
Feito, F.R., Torres, J.C., 1997. Inclusion test for general
polyhedra. Computers & Graphics 22, 1, 23–30.
Gottcshalk, S., Lin, M.C., Manocha, D., 1996. OBB-Tree:
A hierarchical structure for rapid interference
detection. Proc. of the ACM SIGGRAPH 96, 171–180.
Hubbard, P.M., 1996. Approximating polyhedra with
spheres for time-critical collision detection. ACM
Transactions on Graphics 15, 3, 179 – 210.
Jiménez, J.J., Feito, F.R., Segura, R.J., Ogáyar, C.J., 2006.
Particle Oriented Collision Detection using Simplicial
Coverings and Tetra-Trees. Computer Graphics
Forum 25, 1, 53 – 68.
Samet, H., 1990. The Design and Analysis of Spatial Data
Structures. Addison-Wesley.
Schneider, M., Klein, R., 2007. Efficient and accurate
rendering of vector data on virtual landscapes. Journal
of WSCG 15, 1, 59 – 65.
Sherman, W.R., Craig, A.B., 2003. Understanding Virtual
Reality: interface, application and design. Morgan
Kaufmann.
Van den Bergen, G., 2004. Collision Detection in
interactive 3D Environments. Morgan Kaufmann
publishers, Elsevier.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
438
