MULTIREGION GRAPH CUT IMAGE SEGMENTATION

Mohamed Ben Salah

, Ismail Ben Ayed

and Amar Mitiche

1,3

Institut National de la Recherche Scientiﬁque, INRS-EMT, 800 De La Gauchetire Ouest , Montral, QC, H5A 1K6, Canada

GE healthcare, 268 Grosvenor, E5-137, London, ON, N6A 4V2, Canada

Keywords:

Combinatorial optimization, graph cuts, parametric modeling, image segmentation.

Abstract:

The purpose of our study is two-fold: (1) investigate an image segmentation method which combines paramet-

ric modeling of the image data and graph cut combinatorial optimization and, (2) use a prior which allows the

number of labels/regions to decrease when the number of regions is not known and the algorithm initialized

with a larger number. Experimental veriﬁcation shows that the method results in good segmentations and runs

faster than conventional graph cut methods.

1 INTRODUCTION

Image segmentation occurs in many important ap-

plications. It consists of partitioning an image into

regions homogeneous with respect to a given de-

scription. Energy minimization formulations have

led to ﬂexible, transparent, and effective algorithms.

These formulations can be divided into two broad

categories: continuous and discrete (Zhu and Yuille,

1996) (Ayed et al., 2006) (Chan and Vese, 2001)

(Boykov et al., 2006). Continuous formulations,

which seek a partition of the image domain by active

curves via a level set representation, have segmented

accurately a variety of difﬁcult images.

Discrete formulations use objective functions

which contain terms similar to those in continuous

formulations, generally a data term which measures

the conformity of a segmentation to the image data,

and a regularization term. A graph cut formulation

states segmentation as a labeling problem. The graph

cut algorithm assigns each pixel a grey level label

in the set of all possible labels. Thus, the optimiza-

tion of the objective function results in a segmenta-

tion described by a subset of the set of possible labels.

Since no explicit number of regions guides the algo-

rithm, the solution is generally an implicit overseg-

mentation. Also, the use of a set of all possible labels

lengthens the execution time unnecessarily. When the

number of regions is known, one can reduce the num-

ber of labels to equal the number of regions. Regions

can then be described by positive parametric func-

tions, in which case, the data term of the objective

function measures the conformity of the image data

to a parametric model in each region. This formula-

tion was used to state the problem of concurrent seg-

mentation and estimation of image motion (Schoen-

emann and Cremers, 2006). This formulation leads

to an optimization which iterates two steps: contin-

uous optimization with respect to the region parame-

ters and segmentation by discrete graph cut optimiza-

tion. However, the regularization term in (Schoene-

mann and Cremers, 2006), which estimates the length

of the segmentation boundaries assumes the number

of regions known. When the number of regions is not

known beforehand, one sensible formulation would

be to use a larger number initially, to be decreased by

the graph cut optimization algorithm (Boykov et al.,

2001). However, and contrary to the priors used in

(Boykov et al., 2001), the length prior does not allow

this, in general, because merging two disjoint regions

does not change the value of the prior.

The purpose of our study is two-fold: (1) investi-

gate image segmentation which combines parametric

modeling of the image data and graph cut combinato-

rial optimization and (2) use a prior which allows the

number of labels/regions to decrease when the num-

ber of regions is not known and the algorithm initial-

ized with a larger number. As in (Schoenemann and

535

Ben Salah M., Ben Ayed I. and Mitiche A. (2008).

MULTIREGION GRAPH CUT IMAGE SEGMENTATION.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 535-538

DOI: 10.5220/0001081605350538

 SciTePress

Cremers, 2006), the method iterates two steps: closed

form region parameters update and segmentation by

graph cut combinatorial optimization but our regular-

ization term allows region merging.

2 OBJECTIVE FUNCTION

As in (Boykov et al., 2001), and other studies as well

(Chan and Vese, 2001), the objective function con-

tains two terms: a data term to measure the confor-

mity of the segmentation to a parametric model, a

piecewise constant model in this case, and a regular-

ization term to bias the segmentation toward partitions

of the image domain with fewer boundary edges. The

goal is to segment the image into a ﬁxed but arbitrary

number of regions using graph cut optimization of the

objective function. To do so, we use a labeling func-

tion λ : Ω −→ L so that each pixel p ∈ Ω is assigned

the label λ(p) in a ﬁnite set of labels L of cardinal-

ity N

reg

equal to the number of regions. Let R

be the

region of pixels with label l. The solution of the min-

imization, or the ﬁnal labeling, can be represented ei-

ther by the function λ or the partition P = {R

| l ∈ L },

where R

= {p ∈ Ω | λ(p) = l}. The energy functional

to minimize, is formulated using the labeling function

λ, a data term and the regularization term, R :

F (λ) =

∑

p∈Ω

(λ(p)) + α R (λ) (1)

where α is a positive weight. Typically, D

(λ(p)) is

(µ

− I

)

, where I

is the intensity at pixel p and µ

is the value of the label assigned to region R

for 1 ≤

l ≤ N

reg

. We use the following regularization term:

R (λ) =

∑

{p,q}∈N

{p,q}

(λ(p),λ(q)) (2)

where N is the neighborhood set. Function

{p,q}

(λ(p),λ(q)) is a smoothness regularization

function. We consider a regularization function

which is piecewise smooth. More precisely, we

consider the truncated squared absolute difference

model r(λ(p),λ(q)) = min(const,|µ

λ(p)

− µ

λ(q)

)

where const is, in all experimentations, the same used

in (Boykov et al., 2001). The objective function can

be written, for 1 ≤ l ≤ N

reg

, as follows:

F ({µ

},λ) =

∑

l∈L

∑

p∈R

(µ

− I

)

+ α

∑

{p,q}∈N

{p,q}

(λ(p),λ(q))

(3)

3 MINIMIZATION

Minimization of functional (1) is done by alternating

graph cut optimization for segmentation and updating

of labels via continuous optimisation. Given the seg-

mentation, regions parameters are estimated accord-

ing to a closed-form solution. Given the parameters,

the segmentation is updated by graph cut optimiza-

tion.

3.1 Labels Updating

Given a segmentation, a labeling λ is an assignment

of a label λ(p) to each pixel p of the image domain

Ω. Equivalently, it is a partition of Ω into disjoint re-

gions R

where l is the label assigned to pixels of the

region R

. The process of updating labels consists in

estimating these parameters in a way to optimize the

functional when the segmentation is given.

To optimize the functional (3) for a given segmenta-

tion, we proceed by derivation towards the value of a

label µ

∂F ({µ

},λ)

∂µ

= 2

∑

p∈R

(µ

− I

) +

2α

∑

{p,q}∈N ,λ(p)=l

|µ

λ(p)

−µ

λ(q)

|<const

(µ

λ(p)

− µ

λ(q)

) (4)

We choose a neighborhood system, N , of size 4 and

let N

be the set of pixels q neighbors of p which

are assigned a label λ(q) different from, λ(p), the la-

bel assigned to p and verifying |µ

λ(p)

−µ

λ(q)

| < const.

Consequently, equation (4) can be written as

∂F

∂µ

= 2

∑

p∈R

(µ

− I

) + 2α

∑

p∈C

∑

q∈N

(µ

− µ

λ(q)

) (5)

where C

is the boundary of the region R

. The la-

bel value optimizing the functional, given a segmenta-

tion, is deduced from the last equation and expressed

in a closed-form as follows

∑

p∈R

+ α

∑

p∈C

∑

q∈N

λ(q)

♯R

+ α

∑

p∈C

♯N

(6)

where ♯ designates set cardinality.

3.2 Graph Cuts Segmentation Updating

Graph cut optimization was introduced by Greig et

al. (Greig et al., 1989) for image restoration. We

use the algorithm of (Boykov et al., 2001) which has

been used successfully in several vision applications.

The algorithm functions as follows. Let G = hV , E i

be a weighted graph where V is the set of vertices

(nodes) and E the set of edges. V contains a node

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

536

for each pixel and two additional nodes called termi-

nals. There is an edge {p,q} between any two distinct

nodes p and q. A cut C ⊂ E is a set of edges verify-

ing:

• Terminals are separated in the graph G (C ) =

hV ,E \ C i

• No subset of C separates terminals in G (C )

The minimum cut problem consists in ﬁnding the cut

C in a given graph with the lowest cost. The cost of a

cut, |C |, is the sum of its edges weights.

In (Boykov et al., 2001), Boykov et al. present two

algorithms based on graph cuts which ﬁnd a local

minimum of the objective function (3) with respect to

two kinds of large moves: expansion moves and swap

moves. Large moves proceed by changing labels of a

large set of pixels simultaneously to decrease the ob-

jective function. In this work, we use the algorithm

based on swap moves because it handles more gen-

eral energy functionsand deals with the regularization

function that we have chosen.

4 EXPERIMENTATION

To validate the advantages of the method, we present

ﬁrst experiments with synthetic data for noisy piece-

wise constant images. Then we experiment with real

images. The initialization starts with an arbitrary par-

tition of the desired number of regions to which arbi-

trary labels are assigned. the unique free parameter is

the regularization term penalty α.

4.1 Synthetic Data

Figure 1 shows synthetic images representing geo-

metric shapes in the ﬁrst row, the segmentations ob-

tained using the method of (Boykovet al., 2001) in the

second row and the results of the segmentations with

our method in the third row. Contrary to the method

of (Boykov et al., 2001) which uses a set of labels

corresponding to all the possible grey levels, we have

the possibility to initialize the process of segmenta-

tion with the right number of regions, which is known

here, and with an arbitrary set of regions parameters.

The method of (Boykov et al., 2001) allows the num-

ber of labels to decrease due to the regularization term

but it initializes with the set of labels correspondingto

all possible grey levels, i.e., 256 grey levels. The ﬁnal

segmentation is described by a subset of the initial set

of labels and is an implicit oversegmentation since no

explicit number of regions guides the segmentation.

As shown in ﬁgures 1(e)-(h), the segmentation is de-

scribed, in all cases, by a number of regions which is

much larger than the right number of regions: ﬁgure

1(e) is segmented into 98 regions, 1(f) is segmented

into 51 regions, 1(g) is segmented into 58 regions and

1(h) is segmented into 53 regions. On the other hand,

our method allows regions parameters to vary jointly

with the segmentation; thus, the initial set of labels is

arbitrarily chosen and the number of regions is ﬁxed

equal to the right number.

In addition to that, our method realizes a big improve-

ment in term of running time since we deal with a

small number of regions compared to the method of

(Boykov et al., 2001). We show in Table 1 the running

times of the method of (Boykov et al., 2001) and our

method in the case of ﬁgures 1(a)-(d) and the corre-

sponding energies at convergence. In all these exam-

ples, the region merging process allows segmentation

of the images into the right number of regions and we

obtain exactly the same energy and regions parame-

ters at convergence in much less running time.

4.2 Real Data

Though the number of regions is not known, in gen-

eral, for real data, and consequently cannot be ﬁxed in

advance, in most applications a maximum number of

regions is known, i.e., we know that the actual num-

ber of regions is less than some maximum number.

This maximum number is in all cases much smaller

than the number of all possible grey levels as used

in (Boykov et al., 2001). In this section, we deal with

real images and, depending on the application, we ini-

tialize with a number of regions that we consider large

enough to segment the image into an acceptable num-

ber of regions.

The method of (Boykov et al., 2001) is unable to seg-

ment these images into the desired number of regions

and it gives, in all cases, an oversegmentation, in ad-

dition to the much larger time that it takes to converge.

An image such as Figure 2(a) presents smooth varia-

tion of intensity inside the region of interest. Meth-

ods without control on the number of regions frag-

ment that region into multiple segments. The image

in ﬁgure 2(c) presents the biggest running time and

takes 2.90 seconds which is very small compared to

the method of (Boykov et al., 2001) that takes, for the

same image, more than 220 seconds because it deals

with all the possible grey levels and segments it into

200 segments.

MULTIREGION GRAPH CUT IMAGE SEGMENTATION

537

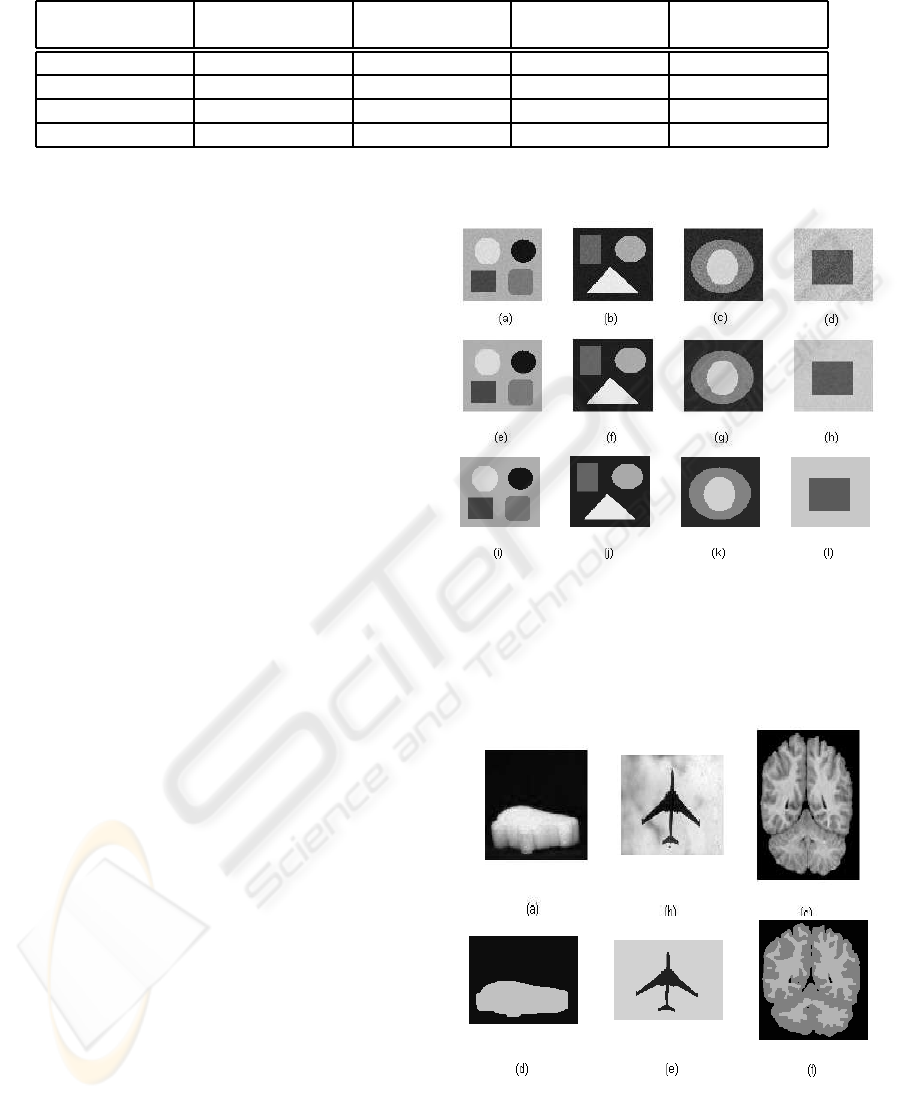
Table 1: Running time and energies of the two methods for synthetic images.

Number of re-

gions

CPU(s): Boykov

et al.

CPU(s): our

method

Energy: Boykov

et al.

Energy: our

method

5 136.12 2.36 15.738 17.640

4 110.01 0.31 14.210 15.701

3 132.40 0.28 27.295 32.784

2 124.90 0.12 32.396 40.650

5 CONCLUSIONS

We presented an image segmentation method which

combines the continuous optimization methods efﬁ-

ciency in describing the segmentation with the com-

putational efﬁciency of graph cuts methods. It al-

lows initializing with just the needed number of re-

gions when it is known or with a larger number oth-

erwise. Parameters vary jointly with the optimization

and convergence is relatively rapid.

REFERENCES

Ayed, I. B., Hennane, I., and Mitiche, A. (2006). Unsu-

pervised variational image segmentation/classiﬁcation

using a weibull observation model. IEEE Trans. on

Image Proc., 15(11):3431–3439.

Boykov, Y., Kolmogorov, V., Cremers, D., and Delong, A.

(2006). An integral solution to surface evolution pdes

via geo-cuts. In ECCV (3), volume 3953, pages 409–

422. Springer.

Boykov, Y., Veksler, O., and Zabih, R. (2001). Fast approxi-

mate energy minimization via graph cuts. IEEE Trans.

on PAMI, 23(11):1222–1239.

Chan, T. F. and Vese, L. A. (2001). Active contours without

edges. IEEE Trans. on Image Proc., 10(2):266–277.

Greig, D. M., Porteous, B. T., and Seheult, A. (1989). Exact

maximum a posteriori estimation for binary images.

Jour. of the Roy. Stat. Soc., 51(2):271–279.

Schoenemann, T. and Cremers, D. (2006). Near real-time

motion segmentation using graph cuts. In Pattern

Recognition (Proc. DAGM), volume 4174 of LNCS,

pages 455–464, Berlin, Germany. Springer.

Zhu, S. C. and Yuille, A. (1996). Region competetion:

Unifying snakes, region growing, and bayes/mdl for

multiband image segmentation. IEEE Trans. on PAMI,

18(9):884–900.

Figure 1: Synthetic images with gaussian noise: (a) 5 re-

gions; (b) 4 regions; (c) 3 regions; (d) 2 regions; (e)-(h):

segmentations with Boykov et al. method; (i)-(l): segmen-

tations with our method. Images size: 128× 128. α = 1.2.

Figure 2: Real data: (a) 2 regions; (b) 2 regions; (c) 3

regions; (d)-(f): segmentations with our method. Images

sizes: (a)154× 115, (b)288× 193, (c)142× 144. α = 2.2.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

538