
A
MULTI-SCALE LAYOUT DESCRIPTOR BASED ON DELAUNAY
TRIANGULATION FOR IMAGE RETRIEVAL
Agn
´
es Borr
`
as Angosto and Josep Llad
´
os Canet
Computer Vision Center - Dept. Ci
`
encies de la Computaci
´
o, UAB Bellaterra 08193, Spain
Keywords:
Layout Descriptor, Scale-Space Representation, Delaunay Triangulation, Content-Based Image Retrieval,
Video Browsing.
Abstract:
Working with large collections of videos and images has need of effective and flexible techniques of retrieval
and browsing. Beyond the classical color histogram approaches, the layout information has proven to be a very
descriptive cue for image description. We have developed a descriptor that encodes the layout of an image
using a histogram-based representation. The descriptor uses a multi-layer representation that captures the
saliency of the image parts. Furthermore it encodes their relative positions using the properties of a Delaunay
triangulation. The descriptor is a compact feature vector which content is normalized. Their properties make it
suitable for image retrieval and indexing applications. Finally, have applied it to a video browsing application
that detects characteristic scenes of a news program.
1 INTRODUCTION
In recent times, the availability of image and video re-
sources on the World-WideWeb has increased tremen-
dously. This has created a demand for effective and
flexible techniques for automatic image retrieval and
video browsing. The early content-based image im-
age retrieval (CBIR) systems used techniques such as
color histograms because they were easy to compute,
robust, and fairly effective (Swain and Ballard, 1991).
Nevertheless, the lack of spatial information makes
color histograms susceptible to introduce false posi-
tives for image retrieval purposes. Then, a wide vari-
ety of techniques have been developed to encode the
spatial layout of the image content.
Some of these techniques consist in refinements
of the color histograms by the spatial coherence of
pixels. Two examples are the color coherence vec-
tor (CCV) (Pass and Zabih, 1996) and the color cor-
relograms (Huang et al., 1997). CCV compute the
color histogram of those coherent pixels of the im-
age, defining coherent as belonging to some sizable
region of the image. In a more precis way, color cor-
relograms express how the spatial correlation of color
changes with distance. Even thought this kind of tech-
niques are compact, simple and easy to compute, they
hardly relay on the image quantization.
Another approach consists in segment the image
into regions and include shape information of the re-
gions. A union of heuristic shape features (bound-
ing box, area, circularity, eccentricity, etc.) are com-
puted for content-based image retrieval (Veltkamp
and Tanase, 2000). Once more, the high dependency
on a good segmentation leads the researchers to avoid
this kind of approaches when dealing with general
purpose systems.
To overcome the segmentation problems, other
approaches such as (Lipson et al., 1997) use pred-
ifined partitions of the image. Then, image classes
are specified by means of photometric and geometric
constraints (e.g. a beach scene is sketched as three
partitions: sky, sea and sand). This approach deals
with a fixed set of pattern configurations, thus is re-
stricted to images of concrete scopes.
Our work consists in the development of a layout
descriptor that try to overcome the weakness of the
previous approaches and accomplishes this set of de-
sirable characteristics:
• Capture the relevance of the parts that conform the
image structure giving more weight to the exten-
139
Borràs Angosto A. and Lladós Canet J. (2008).
A MULTI-SCALE LAYOUT DESCRIPTOR BASED ON DELAUNAY TRIANGULATION FOR IMAGE RETRIEVAL.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 139-144
DOI: 10.5220/0001077501390144
Copyright
c
SciTePress
sive zones of the image than the details.
• Be easy to compute and do not relay to a rigid
and computational intensive image segmentation
procedure.
• Be applicable to any image without classification
restrictions according to predefined layout tem-
plates.
• Be compact and indexable for retrieval proposes.
This paper is organized as follows: in the next sec-
tion we expose the procedure to construct our layout
descriptor and its related work; then, in section 3, we
present some examples and results, and finally, in sec-
tion 4, we resume the main conclusions of our work.
2 LAYOUT DESCRIPTOR
The layout information is a very descriptive cue for
image description. Our work is focused in the con-
struction of a a layout descriptor that encodes the po-
sition and relevance of the image zones. The algo-
rithm follows three main steps:
First we construct a multi-layer representation that
orders the regions by their saliency in relation to the
whole image.
Then, the image zones are identified without re-
quiring high quality segmentation by the means of the
distance function on the edge information.
Finally, in every level of resolution, the relative
positions of the zones are encoded using a triangu-
lation process. The image layout is constructed as a
histogram-based descriptor by joining the information
of all analysis levels.
Next we describe the stages of the descriptor con-
struction while we illustrate the process with an ex-
ample. In Figure 4 we present all the intermediate
images of the descriptor encoding steps.
2.1 Multi-resolution Image
Representation
Linderberg (Lindeberg, 1996) observed that objects in
the world appear in different ways depending on the
scale of observation. He gives as a simple example
the concept of a branch of tree which makes sense
only at a scale from a few centimeters to at most a
few meters, while it is meaningless to discuss the tree
concept at the nanometer or kilometer level.
Besides this multi-scale properties of real-world
objects, image retrieval systems need to cope with the
complexity of unknown scenes and noise. This brings
us to the conclusion that for a deep understanding of
the image structure, multi-resolution image represen-
tation is necessary.
Witkin (Witkin, 1987) and Koenderink (Koen-
derink, 1984) introduced the idea of of generating
coarser resolution images by convolving the original
image with the Gaussian kernel. Thus, the result-
ing structure is known as linear, or Gaussian scale-
space. For a given image f (x,y), its linear (Gaussian)
scale-space representation is a family of derived sig-
nals L(x,y;t) defined by convolution of f (x,y) with
the Gaussian kernel
g(x,y;t) =
1
2πt
e
−(x
2
+y
2
)/2t
(1)
such that
L(x,y;t) = g(x, y;t) ∗ f (x,y) (2)
where t = σ
2
is the variance of the Gaussian.
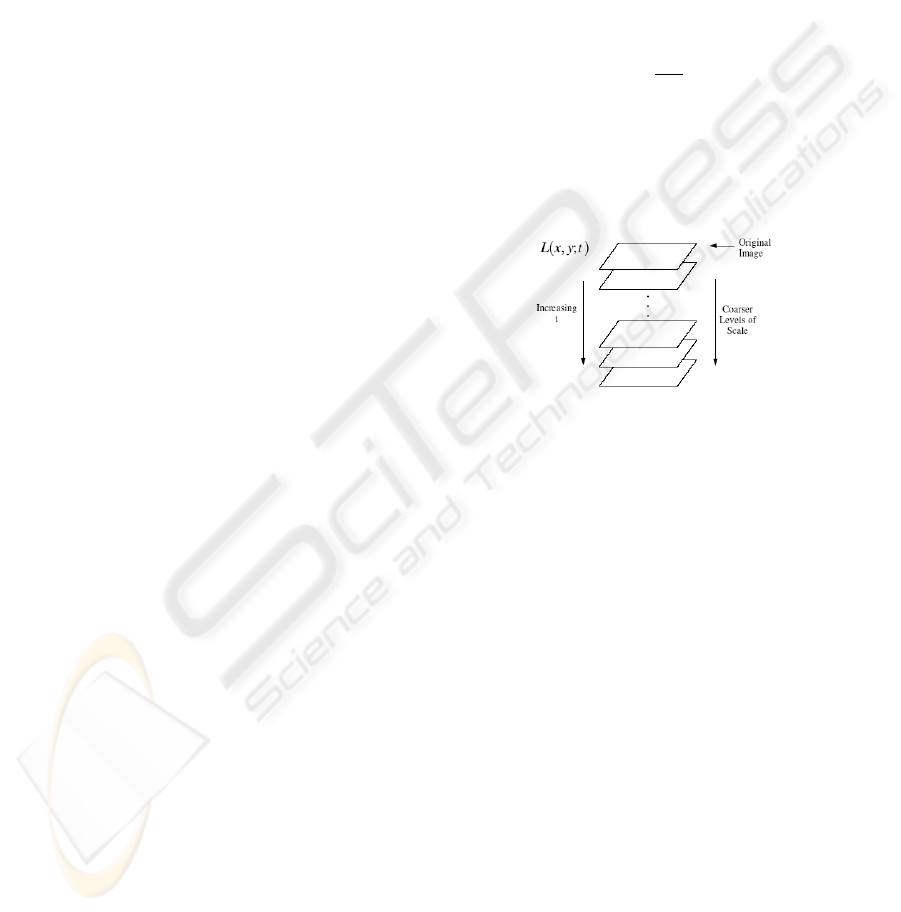
Figure 1: Scale-space image stack.
Such a representation is composed by the stack of
successive versions of the original data set at coarser
scales. It is assumed that, the bigger the scale, the less
information referred to local characteristics of the in-
put data will appear. We use this representation to
analyze the image structures from low resolution to
general information.
2.2 Image Zones Identification
In every resolution level we identify the zones that
compose the image content according the contour
information. Given an image L(x,y;t), we apply
the Canny operator to extract the edge information
E(L;t). We use the image edges as a binary repre-
sentation from which we apply a distance transform
function. The result is a map D(E;t) that supplies
each pixel of the image with the distance to the nearest
edge pixel (Rosenfeld and Pfaltz, 1968). We under-
stand the distance map as a topological surface where
the valleys denote the limits of the image zones. To
identify their positions we take as reference points the
peaks of the ridges P(D;t). Figure 2 shows and exam-
ple of this process.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
140

L(x,y;t) E(L;t)
D(E;t) P(D;t)
Figure 2: Image zone identification.
The image zone identification benefits from a proce-
dure that does not require and intensive image seg-
mentation. The image information can be easily ex-
tracted from the edges and it is not necessary that they
conform closed regions.
2.3 Encoding of the Image Zone Spatial
Arrangement
One we have identified the reference positions of the
image zones we encode their spatial arrangement us-
ing a Delaunay triangulation. The Delaunay triangu-
lation of a point set is a collection of edges satisfy-
ing an ”empty circle” property: for each edge we can
find a circle containing the edge’s endpoints but not
containing any other points. Delaunay triangulations
maximize the minimum angle of all the angles of the
triangles in the triangulation (Delaunay, 1934). These
diagrams and their duals (Voronoi diagrams and me-
dial axes) have been deeply studied and used in many
common methods for function interpolation and mesh
generation. Moreover, there are also many other ways
in which this structure has been applied.
Gagaudakis (Gagaudakis and Rosin, 2003) made
a set of experiments that identified the potential of
measuring indirect shape using the Delaunay trian-
gulation. He measured the performance of the im-
age retrieval adding shape measures to the classical
color histogram descriptors. They considered four-
teen shape methods and test all their possible combi-
nations, giving a total of over 16000 tests. The exper-
iments where focused as a CBIR process applied on
the frames of a video sequence. The tests conclude
that the methods using the triangulation were involved
in the most successful combinations of image feature
descriptors.
Specifically, Tao (Tao and Grosky, 1999) de-
scribed the shape of isolated objects using the spatial
arrangement of the corner points. He applied a Delau-
nay triangulation on these feature points and analyzed
the angular properties of the resulting triangles. The
work introduced a novel method for image indexing
although it failed to be very sensitive on the noise and
the image variations.
In our work we encode the spatial arrangement of
the image zones following a strategy similar to (Tao
and Grosky, 1999) but taking as a feature points the
reference positions of the image zones. Furthermore,
the use of a multi-scale representation allow us to ana-
lyze the image from fine to coarse resolution and over-
come the main drawback of the previous work.
For every image layer we construct a Delaunay tri-
angulation T (P;t) of the coordinate set P(D;t). Then,
a histogram is obtained by discretizing the angles pro-
duced by this triangulation and counting the num-
ber of times each discrete angle occurs in the image.
Given the property that the three angles of a triangle
sum 180 degrees, the histogram is built by counting
the two largest angles of each individual Delaunay tri-
angle. Figure 3 shows an example of the histogram
construction h(T ;t).
P(L;t) T (P;t) h(T ;t)
Figure 3: Layout encoding of a resolution level.
At this point, the layout information of an image is
conformed by the set of the layout histograms h(T ;t)
of each resolution level. Then, we combine all this in-
formation to construct the final image descriptor that
we denote H({h}). With this combination we want
to reach two main objectives: obtain a compact de-
scriptor and accentuate the multi-scale representation
of the image zones. The steps we follow are the next:
first we assemble the set of histograms h(T ;t) as the
rows of a matrix. Then we compute the vertical and
horizontal projections of this matrix and concatenate
both projections in a single histogram. Finally, we
normalize its content to one unit. The vertical projec-
tion enforces the layout of the dominant regions by
adding repetitiveness of their spatial characteristics.
Then the horizontal projection measures the amount
of regions present in each resolution levels. This com-
bination provides a considerably reduction of the in-
formation dimensions. Obtaining a compact descrip-
tor is interesting for indexing applications and stor-
age restrictions. The normalization process allows to
define a closed range of dissimilarity measures. This
fact is useful to study the similarity measure of the im-
ages in retrieval applications. Figure 5 shows graphi-
cally the computation of H({h}).
A MULTI-SCALE LAYOUT DESCRIPTOR BASED ON DELAUNAY TRIANGULATION FOR IMAGE RETRIEVAL
141

L(x,y) E(L) D(E) P(D) T (P) h(T )
t = 1.0
2
t = 1.5
2
t = 2.0
2
t = 2.5
2
t = 3.0
2
Figure 4: Example of the descriptor construction.
Figure 5: Computation steps of the layout descriptor
H({h}) from the histograms of every resolution level
h(T ; t).
3 EXPERIMENTS AND RESULTS
To test our work we have performed some initial ex-
periments on images extracted form a video clip. We
have captured the TV signal from a 24h news station
called 3/24. The signal was captured two frames-per-
second on a total of 5 minutes obtaining a total of 600
images.
First, for each test image we have computed our
layout descriptor. Then, given a query image, the
same feature vector is computed and compared to the
feature vectors in the feature base.
For each test image we have computed our lay-
out descriptor. We have experimentally set to 5 the
number of scale-space layers codified by our repre-
sentation approach, with σ parameter varying from
1.0 to 3.0. Nevertheless, for the rest of parameters
we have based our work in the validation test of (Tao
and Grosky, 1999). Thus, the number of histogram
bins is set to 18 and the Euclidean distance is chosen
as the similarity measure between two descriptors.
The similarity distance allows us to make a voting
process along the time dimension of the video-clip
and find out the appearance of certain characteristic
scenes. Given a query image we observe the similar-
ity of the video-frames. Knowing that H({h}) has 23
bins and normalized content, the dissimilarity mea-
sures are in the range of [0,
√
2]. In the experiments,
we observe that a group of consecutive images with
dissimilarity distance minor than 0.0175 conform a
retrieved scene. Setting an absolute threshold for sim-
ilarity applications is always a hard task. Neverthe-
less, in this video browsing scheme we can benefit
from the time consistence to reject and include ex-
ceptional false positives and negatives.
Figure 6 shows an example of detecting three
characteristic scenes of a news program: the presen-
ter, the program logo and the weather section. Fig-
ure 7 presents two examples of the retrieved scenes
where we can observe the tolerance of the algorithm
to slightly differences on the image content.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
142

a) b)
Figure 6: Detection of the scenes in a video. a)Query image b)X axis represent the image of the video along the time. Y
axes represent the dissimilarity value of the query image. A group of consecutive images which distance is minor than 0.0175
conform the retrieved scene. The first example retrieves three scenes, the second and third examples retrieve one scene.
a) b) c)
Figure 7: Two examples for the same image scenes. We can observe some differences as a) facial expressions, slightly
different viewpoint b) reflection effects c) the image subheading and the dynamic weather symbols.
A MULTI-SCALE LAYOUT DESCRIPTOR BASED ON DELAUNAY TRIANGULATION FOR IMAGE RETRIEVAL
143

4 CONCLUSIONS
We have developed a descriptor that encodes the lay-
out of an image using a histogram-based representa-
tion. The descriptor analyzes the image parts from
a bottom-up direction using a multi-layer represen-
tation. These analysis enforce the representation of
the image parts according to their saliency. Then we
encode their relative positions using the properties of
a Delaunay triangulation. The descriptor is easy to
compute and can be extracted for general purpose in
any image. The descriptor is compact, consist in a
vector of 23 bins, and its content is normalized. These
two properties make it suitable for image retrieval and
indexing applications. Still in a very early evalua-
tion stage, we have applied the descriptor in a video
browsing application. Analyzing the similarity val-
ues of a given image we are able to detect the scenes
along the clip that contain this kind of image. This
work points out to promising results, so our immedi-
ate work is centered in a deeper validation.
REFERENCES
Delaunay, B. (1934). Sur la sph
`
ere vide. Bulletin of
Academy of Sciences of the USSR, (7):793–800.
Gagaudakis, G. and Rosin, P. L. (2003). Shape mea-
sures for image retrieval. Pattern Recogn. Letters,
24(15):2711–2721.
Huang, J., Kumar, S., Mitra, M., Zhu, W., and Zabih, R.
(1997). Image indexing using color correlograms. In
Proc. IEEE Comp. Soc. Conf. Comp. Vis. and Patt.
Rec., pages 762–768.
Koenderink, J. (1984). The structure of images. In Biologi-
cal Cybernetics, volume 50, pages 363–370, Egmond
aan Zee, The Netherlands.
Lindeberg, T. (1996). Scale-space: A framework for han-
dling image structures at multiple scales. In Pro-
ceedings of CERN School of Computing, pages 8–21,
Egmond aan Zee, The Netherlands.
Lipson, P., Grimson, E., and Sinha, P. (1997). Configuration
based scene classification and image indexing. Pro-
ceedings of the 1997 Conference on Computer Vision
and Pattern Recognition (CVPR ’97), pages 1007–
1013.
Pass, G. and Zabih, R. (1996). Histogram refinement for
content based image retrieval. IEEE Workshop on Ap-
plications of Computer Vision, pages 96–102.
Rosenfeld, A. and Pfaltz, J. (1968). Distance functions in
digital pictures. Pattern Recognition, 1:33–61.
Swain, M. and Ballard, D. (1991). Color indexing. Interna-
tional Journal of Computer Vision, 7(1):11–32.
Tao, Y. and Grosky, W. (1999). Delaunay triangulation
for image object indexing: A novel method for shape
representation. In IST SPIE’s Symposium on Storage
and Retrieval for Image and Video Databases VII, San
Jose, California.
Veltkamp, R. and Tanase, M. (2000). Content-based image
retrieval systems: A survey. Technical report, Depart-
ment of Computer Science, Utrecht University.
Witkin, A. P. (1987). Scale-space filtering. In Fis-
chler, M. A. and Firschein, O., editors, Readings in
Computer Vision: Issues, Problems, Principles, and
Paradigms. Kaufmann.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
144
