
ST
ATISTICAL SIGNIFICANCE IN OMIC DATA ANALYSES
Alternative/Complementary Method for Efficient Automatic Identification of
Statistically Significant Tests in High Throughput Biological Studies
Christine Nardini, Luca Benini
DEIS, University of Bologna, Viale Risorgimento 2, Bologna, Italy
Michael D. Kuo
UCSD Medical Center HillCrest, 200 West Arbor Drive, San diego, CA, USA
Keywords:
Statistical testing, statistical significance, multiple hypothesis testing, false discovery rate, statistical resam-
pling methods, statistical meta-analysis, omic data.
Abstract:
The post-Genomic Era is characterized by the proliferation of high-throughput platforms that allow the par-
allel study of a complete body of molecules in one single run of experiments (omic approach). Analysis and
integration of omic data represent one of the most challenging frontiers for all the disciplines related to Sys-
tems Biology. From the computational perspective this requires, among others, the massive use of automated
approaches in several steps of the complex analysis pipeline, often consisting of cascades of statistical tests.
In this frame, the identification of statistical significance has been one of the early challenges in the handling
of omic data and remains a critical step due to the multiple hypotheses testing issue, given the large number
of hypotheses examined at one time. Two main approaches are currently used: p-values based on random
permutation approaches and the False Discovery Rate. Both give meaningful and important results, however
they suffer respectively from being computationally heavy -due to the large number of data that has to be
generated-, or extremely flexible with respect to the definition of the significance threshold, leading to diffi-
culties in standardization. We present here a complementary/alternative approach to these current ones and
discuss performances and limitations.
1 INTRODUCTION
In recent times high-throughput devices for genome-
wide analyses have greatly increased in size, scope
and type. In the post-Genomic Era, several solutions
have been devised to extend the successful approach
adopted for gene expression analyses with microar-
ray technology to other bodies of data such as pro-
teomes, DNA copy number, single nucleotide poly-
morphisms, promoter sites and many more (Nardini
et al., 2006). These data supports, and notably their
integration, represent the future of molecular biology;
for this reason the elucidation and definition of tools
and methods suited to handle the data produced by
these high-throughput devices is of great importance.
Early methods for such analyses were mainly
dealing with gene expression data, their goal being
to extract items that appear to have coherent trends
among themselves (in this context commonly called
unsupervised methods) or with respect to external fea-
tures, such as clinical markers (supervised methods).
Both types of approaches have been used for example
for the classification of subtypes of poorly understood
diseases with unpredictable outcomes (Ramaswamy
et al., 2003; Lapointe et al., 2004). Currently, other
approaches, that take advantage of larger and diverse
sources of information are being devised to address
questions of varying complexity in different areas of
research rooted in molecular biology. These methods
cover a broad variety of applications, from the study
of complex hereditary diseases (Rossi et al., 2006)
to the identification of radiological traits’ surrogate
markers (the molecular origin of a clinical trait) for
enabling non-invasive personalized medicine (Segal
et al., 2007). Overall, besides the variety and com-
plexity of the analyses and methods adopted, some in-
variants can be identified. The most common atomic
step is the identification on the large scale of similari-
ties or associations among molecular behaviors. Such
association measures consist for example of scores
that evaluate similarities across several samples of
genes’ expression profiles, or genetic coherence in
genes copy number or deletion, and more. Coher-
ence among expression profiles and other association
56
Nardini C., Benini L. and D. Kuo M. (2008).
STATISTICAL SIGNIFICANCE IN OMIC DATA ANALYSES - Alternative/Complementary Method for Efficient Automatic Identification of Statistically
Significant Tests in High Throughput Biological Studies.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 56-63
DOI: 10.5220/0001059900560063
Copyright
c
SciTePress

measures can be assessed by means of statistical tech-
niques, namely, by computing a measure of trend sim-
ilarity (test score, θ) and evaluating the likelihood of
this measure to occur by chance (α-level or p-value).
The test score is then assumed to be either a measure
of actual similarity or only a random effect, based on
the value of the associated p-value. The p-value rep-
resents the probability of being wrong when assuming
that the score represents an actual similarity. This er-
ror (type I error) can happen for non-extreme values
of the test θ that are difficult to classify as good or
bad and results in erroneously refuting the null hy-
pothesis (H
0
: θ = 0) which assumes that there is no
relationship, when actual facts show that the items are
tightly related. The scientific community typically
assumes to be meaningful (i.e. statistically signifi-
cant) test scores that are coupled to p-values lower
or equal to one of the following nominal p-values:
0.05,0.01,0.001. These values represent the proba-
bility of committing typeI errors. Given these defini-
tions, the highly dimensional nature of genome-wide
data has posed problems and challenges to conven-
tional biostatistical approaches. Indeed, when per-
forming in parallel such a large number of tests, typeI
errors inherently rise in number, since over a large
number of items, the possibility of faults increases.
For this reason, p-values need to be readjusted in a
more conservative way, accounting for the so called
multiple hypothesis testing issue. The most classical
technique to account for this problem is the Bonfer-
roni correction (R.R.Sokal and F.J.Rohlf, 2003) that
simply multiplies the actual p-value of every single
test by the total number of tests observed. However,
this approach is not considered viable in omic studies,
as in fact it often leads to the rejection of too many
tests, since none of the corrected p-value are smaller
than any of the nominal p-values. An alternative and
less conservative approach to this problem is the gen-
eration of a random distribution, based on random re-
sampling or on the generation of scores obtained from
the randomization of the data. Such approaches allow
to build a distribution that represents the population’s
behavior, and can thus be used to test the hypothesis
of interest. When operating with omic data, another
statistic, the False Discovery Rate (FDR) has been in-
troduced (Benjamini and Hochberg, 1995; Storey and
Tibshirani, 2003; Tusher et al., 2001). Like the p-
value, the FDR measures the false positives, however
while the p-value controls the number of false posi-
tive over the number of truly null tests, the FDR con-
trols the number of false positive over the fraction of
significant tests. The utility of this statistic is unde-
niable, however, its interpretation is far less standard-
ized than the better known
p
-value, and thus, very of-
ten, the value of acceptance of a test based on FDR is
much more flexible and dependent on the investigator
experience. Globally, these characteristics make the
results assessed by FDR highly dependent on the re-
jection level the investigator chooses. This makes it
difficult to automate with high parallelism the iden-
tification of statistically significant hypotheses. This
problem can becomes relevant due to the increasingly
common necessity to merge different sources of in-
formation to assess the validity of a given biologi-
cal hypothesis. Examples of such circumstances arise
whenever, for example, the analysis aims at refining,
by means of cascades of statistical tests, a set of genes
candidate to explain a biological assumption. The
hypothesis in fact is refined collecting information
across various databases or other forms of a priori
knowledge, that progressively filter out the spurious
data -only as an example see various tools presented
in (Tiffin et al., 2006; Rossi et al., 2006). To be ef-
ficient, the analysis requires the result of each filter-
ing step to be automatically sent to the following one.
Thus the possibility to assess significance by mean of
universally accepted values of significance becomes
relevant. This latter observation was one of the stim-
uli motivating the search for an alternative/integrative
approach to the multiple hypotheses problem encoun-
tered when dealing with genomic datasets. We also
wanted this method to be reasonably efficient to be
computed. We thus approached the problem based
on techniques that allow the intrinsic correction of
p-values in case of multiple tests (meta analyses ap-
proaches) used for the combination of various statis-
tical tests. Among them, we turned our attention to
the category of the omnibus tests (L.B.Hedges and
I.Olkin, 1985). These approaches are non-parametric,
meaning that they do not depend on the distribution
of the underlying data, as long as the test statistic is
continuous. In fact, p-values derived from such tests
have a uniform distribution under the null hypothe-
sis, regardless of the test statistic or the distribution
they have been derived from. However, omnibus tests
suffer from a strong limitation: they can be used to as-
sess whether there is a superior outcome in any of the
studies performed. This means that the combined sig-
nificance is not a measure of the average significance
of the studies performed. An omnibus test therefore
cannot be used as is, to assess the global statistical
validity of the number of tests considered simultane-
ously. Thus, we manipulated this approach to make it
applicable to the definition of a significance threshold.
The main advantage of our solution is twofold. On
one side the p-values can be computed in very reason-
able times and can thus help managing the computa-
tional issues related to permutations techniques; on
STATISTICAL SIGNIFICANCE IN OMIC DATA ANALYSES - Alternative/Complementary Method for Efficient
Automatic Identification of Statistically Significant Tests in High Throughput Biological Studies
57

the other side they represent p-values for which nom-
inal threshold of significance (e.g. 0.05, 0.01, 0.001)
can be applied, and can overcome the threshold selec-
tion issue faced when using FDR approaches. Addi-
tionally, this method appears to perform slightly bet-
ter than other methods in avoiding the selection of
false positives. However, this is coupled to a partially
diminished ability in identifying correctly true posi-
tives in complex patterns of association. These con-
sideration support the findings of several authors that
strongly suggest to validate the results obtained from
omic studies through the use of different techniques
and threshold of significance, given the highly noisy
nature of the data (Pan et al., 2005).
2 RELATED WORK
Two main methodologies are currently being used to
approach the multiple hypothesis testing issue. The
first is based on the principles that define the resam-
pling statistical approaches (R.R.Sokal and F.J.Rohlf,
2003). In particular we adopted the permutation
method that requires the construction of a null dis-
tribution to which to compare the actual data. This
distribution must be built from the generation of a
large number of random data. When the distribu-
tion is built using the randomized data generated by
all the tests, the corresponding p-value is corrected
for these same multiple hypotheses. This represents
a structurally simple, robust, but computationally in-
tensive approach, given the large numbers involved
in the analysis of omic data. The computational ef-
ficiency issue can become extremely relevant, since
most of the interpreted languages commonly used for
their large libraries of bioinformatics related functions
(notably R and the Bioconductor Project (Gentleman
et al., 2005), and Matlab), cannot reasonably han-
dle such approaches. Even with the recent improve-
ments for (implicit) parallelization of the computa-
tion, time lags for the evaluation of the results re-
main large. Moreover, for large datasets, compiled
languages such as C also require intensive and long
lasting computational efforts, unless specific archi-
tectures are adopted to enhance efficiency. The sec-
ond approach consists of novel methods purposely
introduced to handle omic data that defines the con-
cept of False Discovery Rate. This statistic comes
in a number of flavors, and relies on complex sta-
tistical assumption. A full description is beyond the
scope of this paper, here we briefly describe three of
the most used approaches: (i) the pioneering work
of Benjamini (Benjamini and Hochberg, 1995); (ii)
the definition of the q-value (Storey and Tibshirani,
2003); (iii) the FDR adopted in the tool Significance
Analysis of Microarray -SAM, (Tusher et al., 2001)- a
widespread software used for the analysis of microar-
ray data.
Benjamini FDR: This approach controls the FDR
by modifying the p-values obtained on a single test,
rescaling it in the following way: FDR
BEN
=
K p
i
i
∑
K
i=1
i
−1
,
where p
i
represents the i-th of the K single p-values.
q-value: The q-value is the minimum false discov-
ery rate. This measure can be approximated by the
ratio of the number of false positives over the num-
ber of significant tests, the implementation of the q-
value provides several options to evaluate this esti-
mate and to compare it to the corresponding p-values.
q ≈ min(#false positives/#significant tests).
SAM FDR: SAM is a tool that allows the ex-
traction of significant genes that help differentiate 2
or more sample classes by means of various scores
suited to answer different questions (i.e. depending
on the number of sample classes observed and on
the meaning of the scores defining the classes, such
as survival times, experimental points in time course
experiments etc.). Statistical validation of the score
value produced by SAM is performed by the genera-
tion of a distribution of random score values. These
scores are evaluated by means of random permuta-
tions of the class labels. These new values, along with
the ones from the original classification are used to
evaluate the FDR as the average of falsely significant
items: FDR
SAM
=
#signi f. permuted scores
#permutations
#signi f . actual scores
i.e. the number
of items with permuted test scores called significant
divided by the number of permutations over the num-
ber of items called significant in actual data.
The q-value approach is one of the most
widespread, both because of its quality and because of
the various and user-friendly implementations the au-
thors have made available. For this reason we choose
this method for comparison to ours. In general, FDR
scores represent an extremely valuable information
while dealing with omic data, however, the main is-
sue to the fully automated use of these techniques lies
in the flexible acceptance of the threshold values for
significance. In other words the investigator can set
his threshold for the acceptance of the False Discov-
ery Rate, but no universally accepted thresholds have
been recognized. This issue has been pointed out for
example in (Cheng et al., 2004). In this work the au-
thors designed three other statistical scores to help in
the choice of the threshold for significance. Among
these scores, two are designed to assess general sig-
nificance threshold criteria for large-scale multiple
tests and one is based on existing biological knowl-
edge. Our method does not represent a novel way to
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
58

evaluate FDR, but it defines a p-value, for this reason
universally accepted thresholds for significance can
be adopted.
More recently and independently from our ap-
proach (Yang and Yang, 2006) have designed a
method based on omnibus tests to improve the identi-
fication of the FDR. Again, one of our goals is to pro-
vide an efficient way to evaluate a p-value that takes
into account the multiple hypotheses tested, in order
to be able to adopt the thresholds of significance ac-
cepted by the scientific community (0.05,0.01,0.001),
easier to automate in long pipelines of tests. In this
paper we show that the p-value obtained with manip-
ulation of the inverse χ
2
method (one of the omnibus
tests) can also be used directly as a measure of sig-
nificance for the identification of statistically signifi-
cantly tests.
3 METHOD
We chose as the base for our approach the inverse
χ
2
method (L.B.Hedges and I.Olkin, 1985), an om-
nibus statistical test used to ascertain if at least one
among several tests is significant, by evaluation of
the following statistics: S(k) = −2
∑
k
i=1
ln(p
i
) and
s(k) = χ
2
(S,2k) where k = 1...K are the tests per-
formed and p
i
the p-value of the i-th test. S has a
χ
2
(s,2k)
distribution, where s is the p-value of the χ
2
distribution with 2k degrees of freedom, and repre-
sents the significance of the combined tests, meaning
that it can assess if any of the tests can be consid-
ered significant, accounting for the total number of K
tests performed. Thus, in the following, s will indi-
cate the p-value we can use for assessing the statis-
tical significance of the tests taking into account the
multiple hypothesis issue, while p will indicate the
significance of the single test. The score θ is the value
resulting from the statistical test. Making use of the
χ
2
inverse method means testing the null hypothesis
H
0
: H
0,1
= ... = H
0,K
= 0. Values of s > 0.05 indi-
cate that H
0
cannot be rejected and thus that it holds
for all the subhypotheses H
0,i
= 0, i ∈ [1, K]. Con-
versely, more than one combination of rejection and
non rejection of single hypotheses H
0,i
is possible to
justify the rejection of the global null hypothesis H
0
.
For example all but one of the subhypotheses could
be null, or only one could be null etc. Evaluating s
on all the tests performed would be of no interest in
terms of defining a global threshold for significance.
In fact, while a non significant value of s would indi-
cate that none of the items has a score value that al-
lows the rejection of the null hypothesis, a low value
of s (< 0.05) would only mean that at least one item’s
score is relevant to the rejection of the null hypothesis,
with no indication on which one(s) are the relevant
items. To overcome this limitation we ranked the tests
scores θ in ascending order (assuming that significant
values of the test are represented by high values of
the score), and ordered the p-values consistently. We
then evaluated s for sets of p-values of increasing size,
starting from a set made of only the p-value corre-
sponding to the worse test score, then adding at each
iteration of this algorithm another p-value coupled to
the immediately higher or equal (better) score (θ), and
closing the last iteration with all the p-values. By in-
duction (Equation 1) we can show that whenever the
value of s drops below any of the standard values of
significance (0.05,0.01,0.001) the score correspond-
ing to the last p-value added is the threshold for sig-
nificance, since it represents the specific test that ac-
counts for the impossibility to reject the global null
hypothesis H
0
. By construction, at each iteration, the
p-value added is always smaller, and correspondingly,
due to the logarithm properties, S shows a fast growth
(S(k) = −2
∑
k
i=1
ln(p
i
)). At the same time the param-
eter of the χ
2
function k, grows linearly (2 · k). Be-
cause of the shape of the χ
2
function and because of
the logarithm properties, if there are enough small p-
values, S becomes quickly and abruptly very large,
and moves to behaviors typical of the ones on the right
hand side of Figure 1(c), χ
2
k
(S) →
k→inf,S→inf
0. This
gives s its typical shape (shown in Figure 1(b)), with a
very abrupt drop from values very close to 1 to values
very close to 0.
For i = 1 s(i) > 0.05 ⇒
H
0
not re j. H
0,1
not re j.
Let i = n s(i) > 0.05 ⇒
H
0
not re j. H
0,i
not re j., ∀i ∈ [1,n]
T hen i = n + 1 s(i) > 0.05 ⇒
H
0
not re j. H
0,i
not re j., ∀i ∈ [1,n + 1]
s(i) ≤ 0.05 ⇒
H
0
re j. H
0,i
not re j., ∀i ∈ [1,n],
H
0,n+1
re j.
(1)
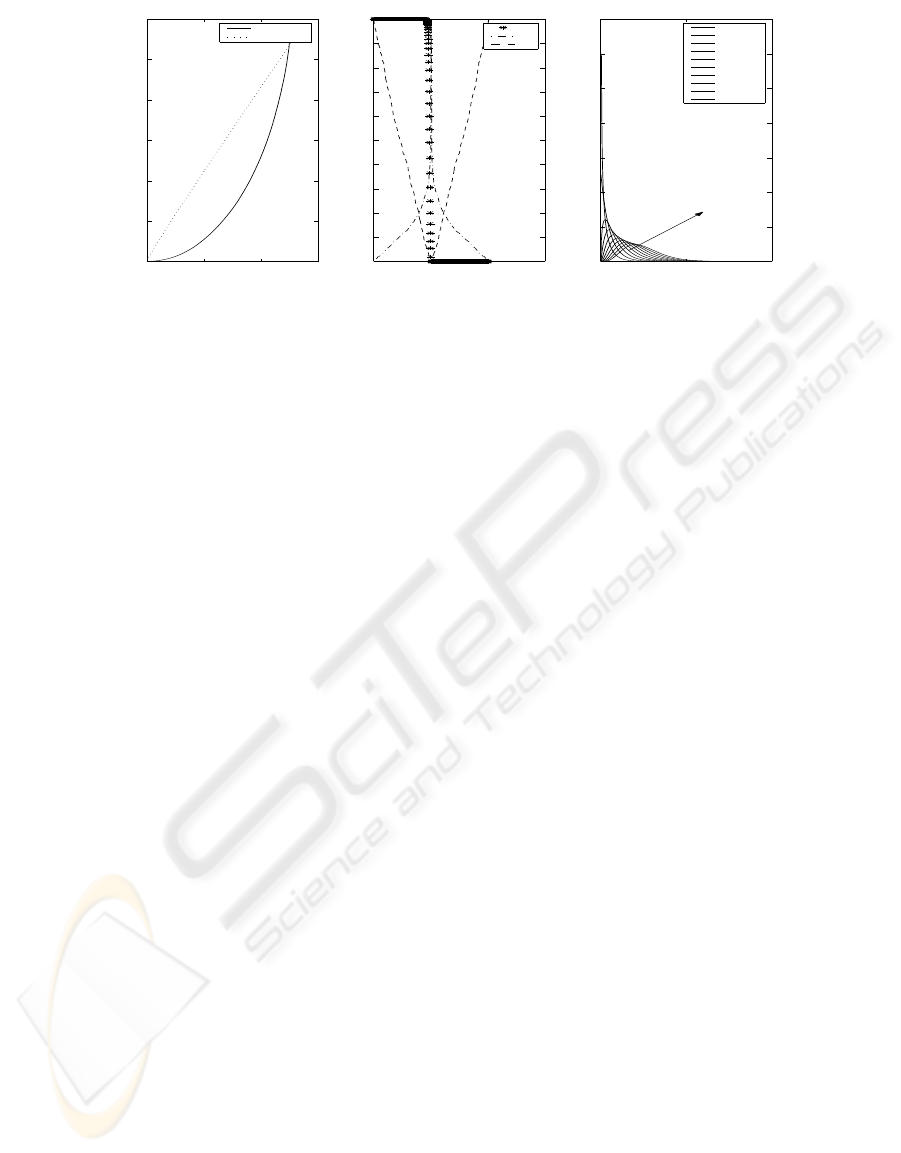
Figure 1 shows an example of the trends of the
variables involved in the evaluation of global signifi-
cance: the statistics S and s that define the global sig-
nificance, the test score θ and the corresponding sin-
gle p-value that are the basic units of the analysis. The
statistic S represents the argument of the χ
2
function
and is associated to a given degree of freedom (k). For
any given degree of freedom it is possible to identify
the minimum value (here called S
idα
) for which the
inverse χ
2
function returns the suited probability α.
Since S
id
is the minimum value, the p-value that rep-
resents the threshold for significance is associated to
k
signα
and can be conveniently visualized as the point
STATISTICAL SIGNIFICANCE IN OMIC DATA ANALYSES - Alternative/Complementary Method for Efficient
Automatic Identification of Statistically Significant Tests in High Throughput Biological Studies
59
0 200 400 600
0
200
400
600
800
1000
1200
Iterations
S (capital)
(b)
S
S
id
0.05
0 500 1000 1500
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Iterations
s(script)
(a)
s
θ
p
0 200 400
0
0.2
0.4
0.6
0.8
1
1.2
1.4
S (capital)
s (script)
(c)
k =1
k =2
k =3
k =4
k =5
k =6
k =7
k =8
k =9
k =10
k
Figure 1: Graphical representation of the different scores involved in the analysis. Figure(a) deals with the statistic S and S
id
.
Figure(b) plots the corrected p-value s, the absolute value of the correlation score θ and the single p-value p. Figure(c) shows
the χ
2
probability density function..
in which k
signα
= k|S
idα
(k) = S(k). Equivalently for s
the threshold for significance at a given nominal level
α can be defined as k
sign
= min
k∈[1,K]
|s(k) ≤ α. In
our experiments θ is the Spearman correlation score
(R.R.Sokal and F.J.Rohlf, 2003). Before processing
the test values we separated positive from negative
scores, and then performed the previously described
operations on the absolute values. This sign segre-
gation of the data has a two-fold objective. On one
side this fulfills the requirement for the applicabil-
ity of the test since one tailed p-values are required.
On the other side it satisfies the biological necessity
to discern between significantly over and under ex-
pressed genes, based on positive and negative values
of the test scores. As far as the permutation approach
is involved we generated 1000 random permutations
of each trait values as it was done in other applica-
tions with this same goal (Liang et al., 2005). We
then re-evaluate the θ scores for all 1000 randomized
instance of each trait, these constitute the null distri-
bution. For the FDR approach, we used the q-value
R package with default settings. For the identification
of significant items, we adopted as threshold the same
values we used for the p-value. The method was im-
plemented in Matlab, scripts for the method are avail-
able upon request.
3.1 Data
To test our method, we simulated the typical set up of
a common genomic experiment. Namely, we gener-
ated a random expression matrix 1000x100 (i.e. 1000
genes and 100 samples) and we defined 5 external
traits for which we search the surrogate markers. In
other words, these external traits mimic any clini-
cal trait or molecular marker. The goal of the ex-
periment is to identify the genes associated to the
external traits, to define the traits’ surrogate mark-
ers. This approach is then used to investigate the
molecular etiology of commonly used clinical mark-
ers. Several examples of such approaches can be
found in literature, only as a sample see (Lapointe
et al., 2004; Liang et al., 2005). At first, we tested
the method’s ability to recognize surrogate markers
of variable size. The surrogate markers were obtained
either by simple copy of expression profiles (in vary-
ing number of copies, namely 0,1,5), or by sum of
varying numbers of profiles (namely 5, 30). The first
group of external traits (#1,#2,#3) provides both the
negative control (0 copies, obtained by elimination of
a randomly chosen expression profile, and exported
as external trait) and helps measuring the compara-
tive ability of the 3 different approaches (FDR, per-
mutations and our method) in extracting small clus-
ter of correlated profiles (1, 5 copies). The second set
of traits (#4,#5) tests the approach with more chal-
lenging data (sums of 5,30 copies). To each ex-
pression value we added varying levels of gaussian
noise (0%,50%,100%) proportional to the expression
value, to better mimic real data (Bansal et al., 2007).
To avoid specific case results, we replicated our ap-
proach 3 times per each noise level and averaged the
results of specificity, sensitivity, positive and negative
predictive value. We observed the approach for the
3 levels of significance 0.05,0.01, 0.001. Finally, we
tested our method to assess its reliability with variable
numbers of genes.
3.2 Multiclass Statistical Scores
To compare our results we evaluated the specificity,
sensitivity, negative and positive predictive value of
the 3 methods: permutations, FDR and ours. These
statistics are used in combination to quantify different
aspects of the accuracy of a binary test, evaluating dif-
ferent proportions of correctly and incorrectly classi-
fied items, when compared to a known classification,
considered the gold standard. In this context the test is
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
60

the ensemble of all the operations performed to clas-
sify each items; positive and negatives label the items
according to the two classes c = N, P = 0,1 they be-
long to; true (T) and false (F) represent the ability of
the test to classify coherently or not a given item in
the test classification with respect to the gold stan-
dard classification. Thus, for example, in classical
definitions TN (true negative) labels items belonging
to class 0 (N) correctly classified by the test, and FP
(false positive) labels items incorrectly classified as 1
(P) by the test. Given these definitions, positive and
negative predictive value (PPV, NPV), sensitivity (Se)
and specificity (Sp) are usually formalized with the
relationships in the first part of Equations 2.
Table 1: Classical definition and generalization to 3 classes
for true, false, negatives, positives.
(a) Classical Definition
Gold Standard
T F
Test
P TP FP → P
t
N FN TN → N
t
↓ ↓
P
gs
N
gs
(b) 3-Classes Definition
Gold Standard
2 1 0
Test
2 T
2
x
12
x
13
→ C
2,t
1 x
21
T
1
x
23
→ C
1,t
0 x
31
x
32
T
0
→ C
0,t
↓ ↓ ↓
C
2,gs
C
1,gs
C
0,gs
When the test classifies n > 2 categories, these
definitions become more complex to apply. However,
it still remains important to be able to characterize the
performances of the test in terms of its ability to dis-
tinguish between items that belong and do not belong
to any category (in our case between genes that con-
stitute and do not constitute any molecular surrogate).
To reach this goal and preserve the meaning of the 4
scores (PPV, NPV, Se, Sp) some caution must be used.
In fact the meaning of positive and negative is not rel-
evant anymore, since there are now positives. Then,
while the definition of true remains straightforward,
as it indicates coherence between the classification of
the test and the gold standard, the definition of false
can be cumbersome, since there are n−1 ways to mis-
classify an item. Additionally, the possibly intuitive
definition of false positives (or negatives as items that
are non-zero in the test (or in the gold standard) clas-
sification leads to ambiguity, since items happen to
be contemporary false positives and false negatives.
To avoid confusion and ambiguities the actual values
of all false can be identified by rewriting the prob-
lem in terms of a system of equation based on the
relationships indicated in Table 1. Here P
t
,N
t
repre-
sent the total number of positive and negative items
that can be found in the test (t) categorization, and
P
gs
,Ngs in the gold standard (gs) classification. The
definitions can be generalized to n > 2 classes chang-
ing the term negative and positive with the indices of
the corresponding classes c = 0,1,...,n, and having
C
c
that designs the total number of positives for each
given class. The system of equations obtained from
the relationships in the rows and columns of Table 1
contains 2 · n equations (i.e. T P + FP = P
t
) and 2 · n
unknown (x
i j
), thus it is completely specified. It is
worth noticing, that with these general definitions, in
case of 2-classes test, Se and Sp appear to be dual
scores. Thus, when generalizing to n-classes it is pos-
sible to define the predictive ability of the test for each
given class c ∈ 0,1,..,n as PV
c
= T
c
/C
t
and the Sensi-
tivity/Specificity (now called Sep) for the same class
c as Sep
c
= T
c
/C
gs
. To clarify the situation it is ex-
tremely useful to rewrite the definitions as they are
written on the left hand side of Equation 2, namely:
PPV = T P/T P + FP) = T P/P
t
PPN = TN/(T N + FN) = TN/N
t
Se = T P/(T P + FN) = T P/P
gs
Sp = T N/(T N +FP) = T N/N
gs
(2)
For n classes this gives:
PPV =
∑
c
T
c
/
∑
c
C
c,t
,c = 1, ..,n
PPN = T
0
/N
t
= T
0
/C
0,t
Se =
∑
c
T
c
/
∑
c
C
c,gs
,c = 1, ..,n
Sp = T
0
/N
gs
= T
0
/C
0,gs
(3)
4 RESULTS AND DISCUSSION
All the results obtained with our method were ob-
tained in much more efficient times compared to the
permutation method, since the computational com-
plexity of our algorithm is O(g·t) while the bootstrap-
ping one is O(g ·t · p), with g indicating the number of
genes, t the number of external traits, and p the num-
ber of permutations. The comparison with FDR in
these terms is not relevant, since this method is com-
putationally efficient. We performed 3 main experi-
ments: the first for comparison among the 3 methods
across all the types of traits (global comparison, Ta-
ble 2); then more specifically, trait by trait (Table 3);
finally we explored the stability of the method across
varying numbers of tests performed.
As far as the first comparison is involved, all meth-
ods performed with varying good degrees of speci-
ficity (Sp > 0.95), but none had satisfactory sensitiv-
ity (Se < 0.5 to Se << 0.5) except the permutation
method for only the threshold 0.05, Se
perm,α=0.05
=
.67. In particular, our method has intermediate sen-
sitivity (better than FDR) and specificity (better than
STATISTICAL SIGNIFICANCE IN OMIC DATA ANALYSES - Alternative/Complementary Method for Efficient
Automatic Identification of Statistically Significant Tests in High Throughput Biological Studies
61
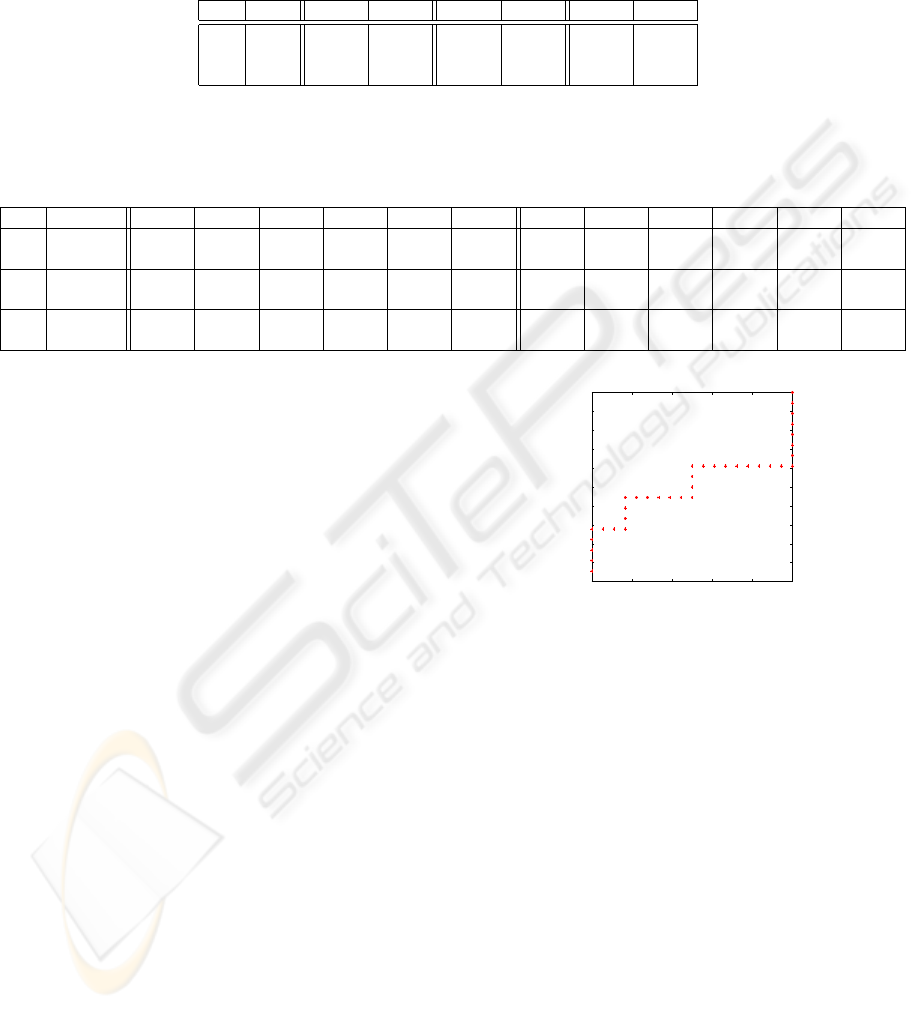
Table 2: Statistics of the performances of the 3 methods compared: our method, permuted p-values and FDR. The comparison
is done on expression matrices 1000x100 and 5 traits as they are described in Section 3.1. Results are averaged over 3
instances of the random data generated with the same specifics. Standard deviations of these averages are below 10
−2
. The
first column indicates the noise level (n), the second the threshold of significance chosen (α) and then all the scores for the 3
methods. Because of space constraints only values for noise 0.5 are shown.
Our Method Permutations FDR - q-value
n α Se Sp Se Sp Se Sp
.05 .1905 .9998 .6746 .9512 .1667 .9948
0.5 .01 .1667 .9999 .4603 .9898 .1667 .9948
.001 .1667 1.000 .3175 .9981 .1667 .9948
Table 3: Class by class comparison of the algorithms performances. Our method performs better in terms of avoiding false
positive ans worse with false negatives. Data are shown as averages across the random replicates and across the 3 different
levels of significance, for 3 different levels of noise (n). Figures in italic were inferred from NANs.
PV (classes) Sep (classes)
n Method 0 1 2 3 4 5 0 1 2 3 4 5
Ours .9998 1.000 1.000 1.000 .3111 .0556 .9936 1.000 1.000 1.000 0.000 0.000
0 Perm. .9797 1.000 1.000 1.000 .9556 .2852 .9956 .2510 0.000 .3846 .4325 .3494
Ours .9999 1.000 1.000 1.000 .0444 .0037 .9931 1.000 1.000 1.000 0.000 0.000
0.5 Perm. .9797 1.000 1.000 1.000 .9556 .2852 .9956 .2510 0.000 .3846 .4325 .3494
Ours .9999 .3333 1.000 .7333 .0000 .0037 .9925 0.000 1.000 .9506 0.000 0.000
1 Perm. .9797 1.000 1.000 1.000 .9556 .2852 .9956 .2510 0.000 .3846 .4325 .3494
permutations). Since the FDR method at the chosen
thresholds for significance appears to behave in ex-
treme ways, i.e. with better specificity and worse sen-
sitivity with respect to both methods, we focused our
attention to a more refined comparison between the
bootstrapping method and ours, and did not pursue
the goal, out of our scope here, to evaluate results with
other thresholds for significance.
Namely, we performed the second experiment, on a
trait by trait basis, with two goals: to investigate the
reasons of the improved performances of our method
in terms of specificity; to assess the reasons for the
poor global performances in terms of sensitivity. For
this we evaluated PV and Sep for each one of the 6
classes (c = 0,1,..,n). In general our method seems
to have more problems with false negatives, while the
bootstrapping method collects a much larger number
of false positives (Table 3). These characteristics de-
pend on the intrinsic properties of s as they have been
described in Section 3. The abrupt drop in value of
s is responsible for an almost binary behavior of this
score. This leaves very little gray areas for spurious
classification, thus ambiguous θ values are quickly
coupled to high s values and discarded from the sig-
nificant tests set. Overall, trait #5 defines a too com-
plex pattern (sum of 30 profiles), and none of the
method can treat it correctly, conversely, trait #4 (sum
of 5 profiles) can be superiorly handled by the permu-
tation method and trait #1, #2 and #3 (1,0,5 corre-
lated profiles) are better recognized with our method.
It is difficult to speculate on whether surrogate mark-
ers of type #3 are more or less common than the ones
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
False Positive Fraction
True Positive Fraction
Figure 2: ROC curve for PV, AUC ≈ 0.6.
of type #4 in actual biology, we can state however that
our method is able to identify the surrogate markers
of trait #3 with profiles that have as little correlation
as 0.33 (100% noise addedd). To summarize these
results we evaluated ROC curves to assess if any of
the methods was strikingly outperforming the other
(ROC curves in this case are not used to evaluate the
relationship between sensitivity and specificity, but to
compare two populations of data, that happen to be
PV and Sep scores). We compared: (i) PV and Sep
for each method, (ii) Sep only, (iii) PV only. Namely,
sensitivity and specificity combined, as well as sensi-
tivity alone lead to AUC ≈ 0.5, while the specificity
test leads to AUC ≈ 0.6, slightly better, but not statis-
tically significant (Figure 2, AUC = 0.5 indicates tests
with comparable performances).
Finally, we tested our method for the same hy-
potheses for varying numbers of genes, from 100 to
2000 (steps of 100 genes). Across 20 samples we ob-
tained median values that reproduce the findings of
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
62

the two previous experiments (global and trait by trait
performances) with very small variances across the 20
samples (≈ 10
−2
for sensitivity and ≈ 10
−3
for speci-
ficity). Thus, the method appears to be stable with
respect to the number of items tested.
5 CONCLUSIONS
We presented a method for the identification of p-
values in omic studies. This approach is based on a
meta-analysis and has two main advantages. On one
side it is computationally efficient, and can thus be
used in interpreted languages such as R and Matlab
that offer rich libraries of functions for omic analyses.
On the other side it is based on the identification of
a p-value rather than FDR, and can thus take advan-
tage of nominal threshold for significance, allowing
for an easier automation of filtering steps in analyses
based on statistical tests. Conversely to the permuta-
tion technique, that remains a computationally inten-
sive but very robust reference method, our approach,
globally, appears to be more specific but less sensi-
tive. This improved specificity can be extremely ad-
vantageous in the practice of Systems Biology, since
novel compact functional subunits can emerge or re-
main uncovered and require longer and costly exper-
imental investigations to be extracted, depending on
the noise they appear to be identified with. Applica-
tion to real data needs to be provided and this repre-
sents our current research activity. For these reasons
we believe the definition of alternative and comple-
mentary method is appropriate.
ACKNOWLEDGEMENTS
The authors would like to thank Diego di Bernardo
and Mukesh Bansal for constructive discussion.
REFERENCES
Bansal, M., Belcastro, V., Ambesi-Impiombato, A., and
di Bernardo, D. (2007). How to infer gene networks
from expression profiles. Mol Syst Biol, 3.
Benjamini, Y. and Hochberg, Y. (1995). Controlling the
false discovery rate: a practical and powerful ap-
proach to multiple testing. J.R. Stat. Soc. B, 57:289–
300.
Cheng, C., Pounds, S., Boyett, J., Pei, D., Kuo, M., and
Roussel, M. F. (2004). Statistical significance thresh-
old criteria for analysis of microarray gene expression
data. Stat Appl Genet Mol Biol, 3:Article36.
Gentleman, R., Carey, V., Huber, W., Irizarry, R., and Du-
doit, S. (2005). Bioinformatics and Computational Bi-
ology Solutions Using R and Bioconductor. Springer.
Lapointe, J., Li, C., Higgins, J. P., van de Rijn, M., Bair,
E., Montgomery, K., Ferrari, M., Egevad, L., Rayford,
W., Bergerheim, U., Ekman, P., DeMarzo, A. M., Tib-
shirani, R., Botstein, D., Brown, P. O., Brooks, J. D.,
and Pollack, J. R. (2004). Gene expression profiling
identifies clinically relevant subtypes of prostate can-
cer. Proc. Natl. Acad. Sci., 101(3):811–816.
L.B.Hedges and I.Olkin ((1985)). Statistical Methods in
Meta-Analysis. Academic Press, New York.
Liang, Y., Diehn, M., Watson, N., Bollen, A. W., Aldape,
K. D., Nicholas, M. K., Lamborn, K. R., Berger,
M. S., Botstein, D., Brown, P. O., and Israel, M. A.
(2005). Gene expression profiling reveals molecularly
and clinically distinct subtypes of glioblastoma multi-
forme. Proc. Natl. Acad. Sci., 102(16):5814–5819.
Nardini, C., Benini, L., and Micheli, G. D. (2006). Circuits
and systems for high-throughput biology. Circuits and
Systems Magazine, IEEE, 6(3):10–20.
Pan, K.-H., Lih, C.-J., and Cohen, S. N. (2005). Effects
of threshold choice on biological conclusions reached
during analysis of gene expression by DNA microar-
rays. Proc. Natl. Acad. Sci., 102(25):8961–8965.
Ramaswamy, S., Ross, K. N., Lander, E. S., and Golub,
T. R. (2003). A molecular signature of metastasis in
primary solid tumors. Nat. Genet., 33(1):49–54.
Rossi, S., Masotti, D., Nardini, C., Bonora, E., Romeo, G.,
Macii, E., Benini, L., and Volinia, S. (2006). TOM:
a web-based integrated approach for efficient identifi-
cation of candidate disease genes. Nucleic Acids Res.,
34(doi:10.1093/nar/gkl340):W285–W292.
R.R.Sokal and F.J.Rohlf (2003). Biometry. Freeman, New
York.
Segal, E., Sirlin, C. B., Ooi, C., Adler, A. S., Gollub,
J., Chen, X., Chan, B. K., Matcuk, G. R., Barry,
C. T., Chang, H. Y., and Kuo, M. D. (2007). De-
coding global gene expression programs in liver can-
cer by noninvasive imaging. Nature Biotechnology,
25(6):675–680.
Storey, J. D. and Tibshirani, R. (2003). Statistical signifi-
cance for genomewide studies. PNAS, 10(16):9440–
9445.
Tiffin, N., Adie, E., Turner, F., Brunner, H., van Driel nd
M. Oti, M. A., Lopez-Bigas, N., Ouzunis, C., Perez-
Iratxeta, C., Andrade-Navarro, M. A., Adeyemo,
A., Patti, M. E., Semple, C. A. M., and Hide,
W. (2006). Computational disease gene identifica-
tion: a concert of methods prioritizes type 2 dia-
betes and obesity candidate genes. Nucleic Acids Res.,
34(doi:10.1093/nar/gkl381).
Tusher, V. G., Tibshirani, R., and Chu, G. (2001). Sig-
nificance analysis of microarrays applied to the ion-
izing radiation response. Proc. Natl. Acad. Sci.,
98(9):5116–5121.
Yang, J. J. and Yang, M. C. (2006). An improved procedure
for gene selection from microarray experiments using
false discovery rate criterion. BMC Bioinformatics,
7:15.
STATISTICAL SIGNIFICANCE IN OMIC DATA ANALYSES - Alternative/Complementary Method for Efficient
Automatic Identification of Statistically Significant Tests in High Throughput Biological Studies
63
