
MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS
GRAMMAR
Herbert F. Jelinek and Audrey Karperien
School of Community Health, Charles Sturt University, Albury, Australia
Keywords: Microglia, L-systems grammar, modelling, pathology.
Abstract: Medical image analysis requires in the first instance information on the extent of normal variation in a
biological system in order to identify pathological changes. MicroMod is an L-systems based software
package available through the World Wide Web that allows modelling of complex branching structures
such as neurons and glia using deterministic or probabilistic algorithms. In addition, MicroMod includes
software for assessing complex structures using methods such as fractal and lacunarity analysis. We
demonstrated through fractal analysis of simulated microglia that MicroMod can be used for modelling and
measuring different stages of microglial activation. The fractal dimensions of microglia visualised using
histochemical techniques showed good agreement with our models made using MicroMod, and changes in
complexity and heterogeneity as seen during activation and response to pathology were well emulated by
modifying a few essential parameters (sub to parent branch length, sub to parent branch diameter, and sub
branch number). These results indicate that MicroMod provides a useful adjunct to neuroscience research
into understanding complex changes in structure associated with normal function and disease processes.
1 INTRODUCTION
The modelling programme described and discussed
here was inspired from research into the morphology
of a type of cell called microglia. These small cells
are a critical component of the brain’s immune
system, and have been called the brain’s “first line
of defence” for the critical roles they play in
mediating effects of injury and disease in the central
nervous system. (Kreutzberg 1995)
The feature of microglia particularly relevant to
this paper is their dynamic morphology. To explain,
microglia normally reside in the brain in a highly
branched resting morphology. In this form,
microglial cell bodies are small and elongated or
rounded, surrounded by multiple relatively thin
extensions known as microglial processes that
themselves branch to finer and finer levels of
ramification, extending around neurons and other
cells deep into the surrounding neural tissue, as
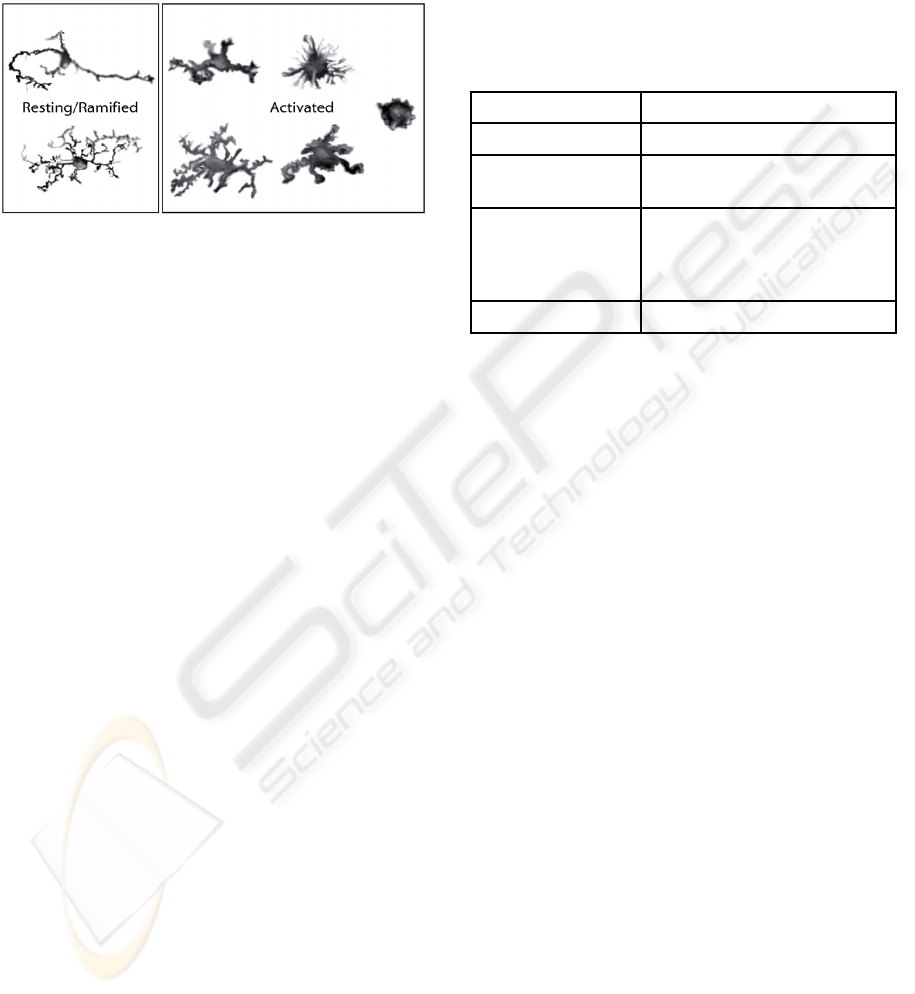
illustrated in Figure 1.
Resting microglia are thus perfectly postured to
continually sample their environment and respond to
the earliest signs of insult or injury in the
surrounding structures and milieu of the central
nervous system, but their role goes beyond that of
patrolling sentinel. If they detect problems,
microglia can change dramatically from their
Figure 1: Resting microglia are highly branched immune
system cells found in the brain.
289
F. Jelinek H. and Karperien A. (2008).
MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS GRAMMAR.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 289-294
DOI: 10.5220/0001059802890294
Copyright
c
SciTePress
highly ramified, resting sensor morphology to an
unbranched, rounded to amoeboid form that is
increasingly motile and phagocytic (Soltys,
Orzylowska-Sliwinska et al. 2005). As illustrated in
Figure 2, this change occurs along a continuum of
subtle to obvious differences in morphology.
Figure 2: Typical microglial morphologies. Processes
retract and the soma becomes rounder and expands as
microglia become increasingly activated to respond to
pathological changes.
The morphology a microglial cell might be found
to adopt reflects variables such as the cell’s position,
surroundings, and motion, but also generally
corresponds to differences in functional capacity and
activity. Indeed, the relative amounts of microglial
cells adopting certain morphological configurations
vary in different diseases and in different stages of
the progression of individual disease states (e.g., the
overall profile of microglial morphology typical in
schizophrenia can be differentiated from that in
Alzheimer’s disease) (Jelinek, Karperien et al.
2004). It is therefore essential to obtain a good
understanding of even subtle changes in microglial
form along the continuum of morphological variety,
and to be able to relate these changes to cell
characteristics (Cornforth, Jelinek et al. 2002).
1.1 The MicroMod Modelling Software
MicroModV6.0 is biological cell and fractal structure
modelling software written in Java by one of the
authors (AK), using the NetBeans IDE 3.5 on the
Java 2 Platform v1.4.2 (Jelinek, Karperien et al.
2002). The programme has been tested on
WindowsXP Pro, Windows2000, Windows98, and
SUSE Linux. It is available as a stand-alone Java
application from Charles Sturt University as
MModLE.jar (source code is available on request).
MicroMod contains 28,456 lines of code, 19,313
non-comment lines, and 7,818 comment lines of
code. Features available in MicroMod are shown in
Table 1.
In addition to the models described in the rest of
this paper, MicroMod software renders for
benchmarking and analysis statistical or
deterministic, skinny or fat fractals, including
quadric, Koch, Menger, and Sierpinski fractals;
multifractals such as various Henon Maps; other
iterated fractal structures (e.g., ferns); and diffusion
limited aggregates.
Table 1: MicroMod Features.
MicroModsrc Main package
MicroModsrc.GUI Graphic user interface
MicroModsrc.Help
User's guide in html for swing
browser
MicroModsrc.MakeSt
ructure
Methods for generating random
and deterministic fractals as well
as branching structures for cell
modelling
MicroModsrc.Utils Utilities
Structures can be viewed on a display screen or
saved to a hard drive as either images (.jpg or .png
format) or MicroMod model files (.mod format). All
models can be rendered and saved in coloured,
shaded, gray-scale, and binary formats. Structures
are generated from built-in configurations or
loadable .mod files (some provided with
MicroMod), or from parameters set by the user.
Configurable options include structural parameters
and various rendering options such as background
colour or whether to view a structure grow or not.
All models can be modified, saved, and reloaded,
and can be used to generate single images or sets of
multiple images.
MicroMod also includes a fractal analysis
function. Structures can be assessed on the screen as
they are generated or in batches of images from the
user's hard drive. The analysis is delivered on screen
and in detail in a text file that can be loaded in a
spread sheet. The fractal analysis algorithms of
MicroMod are also available in the FracLac
software, a plug-in for ImageJ freely available from
the US National Institutes of Health (Karperien
2007).
2 MODELLING WITH
MICROMOD
To simulate biological structures such as microglia,
MicroMod employs L-systems principles. As
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
290
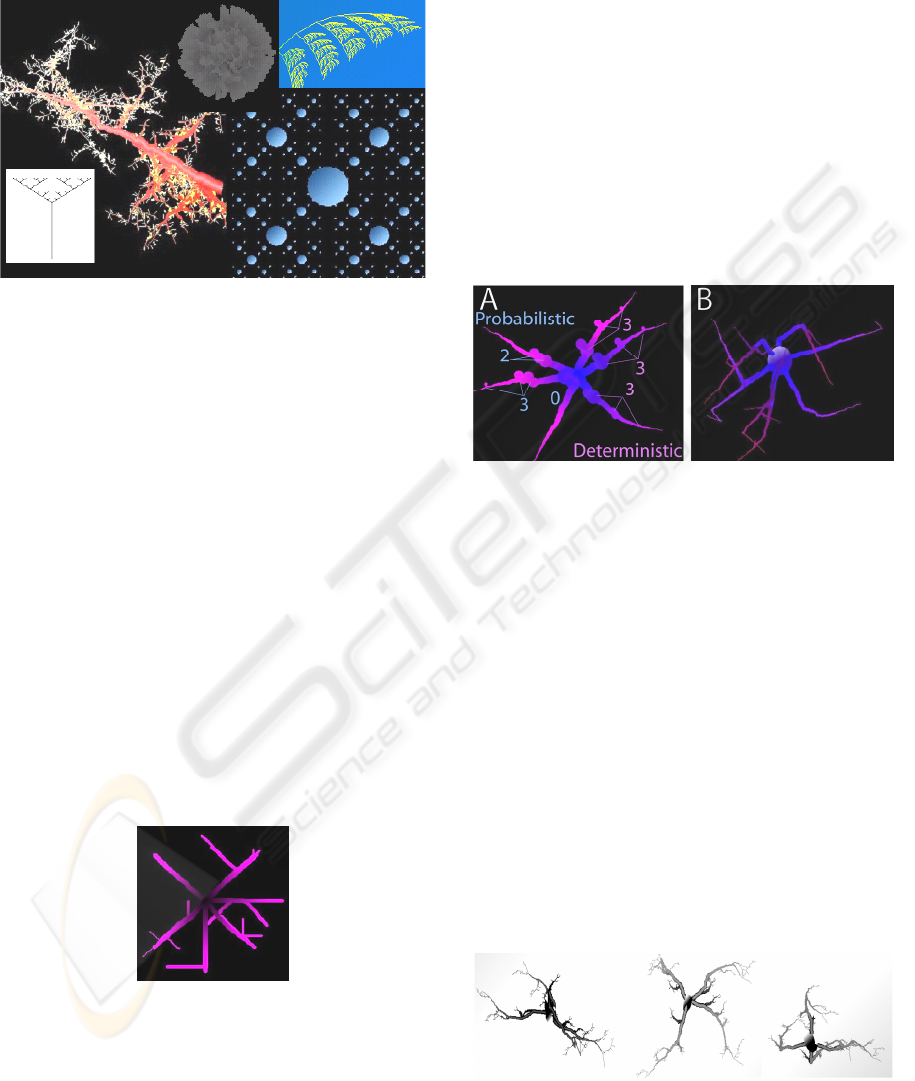
illustrated in Figure 3, a variety of structures at
different levels of complexity can be generated using
L-systems.
Figure 3: Examples of structures modelled in MicroMod
using L-systems principles.
The fundamental algorithm used for modelling
microglia is based on MicroMod’s built-in
branching model. The algorithm generates sets of
symbols to be rendered on the computer screen. For
modelling microglia, one set specifies features for
one microglial process, where each point within
each set specifies the size, shape, colour, and
location of a structural element of the process, and
rules set by the user are applied recursively to evolve
each original set into a more complex structure.
To elaborate, the simplest branching model is a
set of points representing straight lines, and the next
level of complexity is a set with one level of sub-
branches (Figure 4). Such a model can be altered by
changing various parameters including the rate of
acquiring branching points and the number of
branches that sprout at each branching point; the
ratio of the length and diameter of daughter branches
to the length of the parent; and the taper for each
branch.
Figure 4: Radial model generated by specifying a
minimum number of parameters.
Gross structural features such as the area and general
shape of the central soma and the number, length,
and diameter of primary branches can also be
changed. In addition, directional features such as the
probability of a branch continuing in a direction
(related to the tortuousness of a process) and the
angle of branching can be set. Moreover, to further
explore variation within a cell or compare cells, the
user can modify individual processes of a cell
separately.
Furthermore, several of the parameters
describing a process, such as branching rate and
tortuousity, can be applied as probabilities rather
than fixed values (Figure 5). Figure 5A, for instance,
illustrates a simple radial model generated using a
probability (rather than a deterministic value) for the
number of branches along each primary branch,
whereas Figure 5B shows a simple radial model
rendered with a deterministic branching rate but
probabilistic tortuousity features.
Figure 5: Simple branching models. Within each model,
all branches are statistically identical. 5A. Random
Variation in Branching Frequency. Nodes show locations
for daughter branches on primary branches. All nodes
were sprouted at one statistically identical rate; however,
nodes on branches extending right were generated
deterministically and on branches extending left were
generated probabilistically. 5B. Random Variation in
Branching Angle and Tortuousity. Daughter branches
were sprouted at one deterministic rate on all primary
branches, but their rate and angle of change in direction
were determined probabilistically.
The significance of having probabilistic
parameters available for modelling microglia is that
the opportunity exists to generate each cell process
as a statistically identical but unique structure. The
user can, accordingly, explore overall features of a
class of structures by generating groups of
statistically identical but unique images from a
single set of parameters (Figure 6).
Figure 6: Statistically identical but unique models of
resting microglia generated using one set of parameters.
MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS GRAMMAR
291
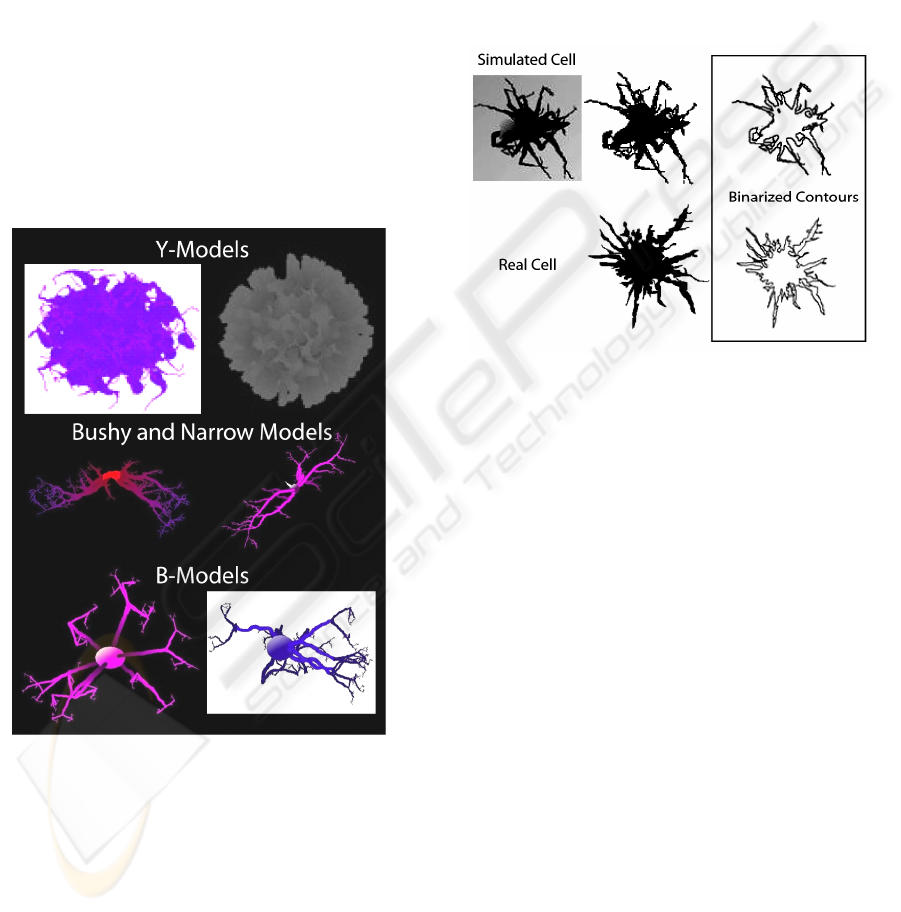
As was noted in the introduction, microglia adopt a
wide variety of conformations when they respond to
events in nervous tissue. For modelling microglia
and other biological cells, MicroMod has several
models in addition to the radial model just discussed.
Examples of the MicroMod outputs of the Y-model,
the bushy and narrow models, and the B-model are
shown in Figure 7. The Y-model (top of Figure 7)
provides large spherical to amorphous structures
with short tapered and unbranched projections. The
bushy model and the narrow model are similar, but
allow branch diameters and the degree of sprouting
to be set. These models specify how tortuous images
are using the single angle functions in MicroMod.
The B-Model includes options for multiple,
bifurcating branches as well as for setting branch
angle, length, tortuosity and twist. The number of
branches and number of sprouts can be modified
using the menus.
Figure 7: Modelling options for branched cell structures
available in MicroMod.
3 ANALYSING MICROGLIAL
ACTIVATION USING
SIMULATED MICROGLIA
Populations of cells were modelled from real
microglia, based on measurements such as the length
and number of branches and the ratios of daughter to
parent branch length and diameter. To most closely
emulate real, dynamic microglia in their natural
environment, cells were generated using
probabilistic values. Using box-counting fractal
analysis we compared the simulated cells to the real
after converting digital images to binary in order to
assess the complexity of the cell contour. As
indicated in previous research, there was close
agreement between simulated and real cells (Figure
8) on the box counting dimension (D
B
). (Smith,
Marks et al. 1989; Jelinek, Karperien et al. 2002)
Figure 8: Real compared to simulated microglia. The real
cell had a fractal dimension of 1.423 compared to the
simulated of 1.425.
3.1 Scaling Features
To assess the sensitivity of MicroMod for modelling
subtle morphological changes associated with
different levels of microglial activation, we
manipulated several features of the models and
assessed both complexity as measured by the D
B
and
heterogeneity (lacunarity or Λ). Manipulating the
size and shape of the modelled soma had essentially
no effect on the D
B
, but a slight effect on Λ, where
in general models with larger and more elongated
somata had lower values for Λ. Both the D
B
and Λ
were affected by changing the number of primary
branches, but the effects were not consistent.
Changing scaling features, in contrast, had several
noteworthy effects. Changes were made in a manner
consistent with fractal changes, as the results are
predictable and therefore useful in judging the utility
of the software.
Figure 9 shows that the D
B
and Λ changed when
the length of sub-branches relative to the parent
branch was changed but the number of sprouts
remained the same. Similarly manipulating the scale
of sub to parent branch diameter and the number of
new branches per branch affected the D
B
.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
292

Figure 9: Effect of varying cell features on fractal
dimension and lacunarity.
Changing the scaling of sub-branch diameter had
no effect on either the D
B
or Λ for models with
narrow branches, owing to the finite limit on the
smallest possible diameter of a branch. For models
with larger starting diameters, however, the ratio of
sub-branch to parent diameter affected the D
B
. The
D
B
and Λ were strongly positively correlated for
models with wider branches, but not as strongly for
models having narrower branches. The D
B
mainly
decreased as the length of primary processes
decreased, as when microglia withdraw their
processes in response to noxious stimuli in their
environment, for example. Although Λ decreased
overall with decreasing primary process length, it
initially increased for smaller branch diameters (i.e.,
models resembling resting more than activated
cells).
Cells differing only in branch diameter were
modelled to emulate process swelling in isolation
from other changes—i.e., only the diameter of
primary branches (measured where they leave the
soma then allowed to taper according to a fixed rate)
was manipulated. Both the D
B
and Λ were affected
by changing this feature, but there were some
differences in the effects. As long as branch
diameter remained relatively narrow compared to
soma span, the D
B
rose slightly as branch diameter
increased. As branch diameter continued to increase,
however, owing to crowding of "swollen" processes,
some detail disappeared from the final binary
patterns extracted from the images. In contrast, Λ
decreased without increasing as branch diameter
increased, and the effect was more noticeable at
smaller diameters than it was for the D
B
. In addition,
models with greater tortuousity had higher D
B
and
lower Λ values.
4 CONCLUSIONS
Previous research has shown that microglial
morphology can be modelled with high fidelity
using MicroMod. In addition, recent investigations
have revealed that the D
B
and Λ can be used to
measure the types of graded changes in microglial
morphology typically associated with microglial
activation. (Jelinek, Karperien et al. 2002) The work
presented here goes a step further in describing how
the progression from ramified to activated (i.e.,
nonpathological to pathological) in microglia can be
accurately modelled and cellular complexity
assessed by progressively changing a few essential
parameters.
It is important to note that the modelling of
microglial activation described here is deliberately
subject to random variation. For perfect patterns
extracted from perfect theoretical models, the D
B
measures fundamental complexity and Λ measures
heterogeneity. From a practical perspective applied
to real cells, though, they will measure at once a
composite of several features. Because of the
considerable morphological variation attributable to
not only activation but also the space microglia
occupy and the orientation they assume at any point
in time, variation is predictable when finding D
B
s
even for cells in equivalent activation states having
essentially the same branching ratios. As was shown
here, despite that a microglial model's inherent
complexity is specified by known recursively
applied rules, an extracted pattern may not
necessarily convey this fundamental pattern's
original information fully and without distortion. In
real cells, the underlying mechanisms of
morphological transformation are also not
necessarily conveyed in values extracted from real
contexts. But microglia are biological structures we
hope to understand and assess ultimately in their
natural environs. Analyses that can be used in this
way have practical advantages over assessments
based on uncomplicated theoretical models, and
modelling, as was shown here, helps bridge our
knowledge of practical influences.
In conclusion, the work we report here may have
important implications for understanding the events
of microglial activation associated with different
states of health and disease. Simulated cells, readily
available in large numbers and extremely
manipulable, increase the opportunities to
objectively study morphological changes and
random variation in microglia. MicroMod, thus,
presents a useful adjunct to neuroscience research
into understanding complex changes in structure
associated with normal function and disease
processes.
MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS GRAMMAR
293

REFERENCES
Cornforth, D., H. F. Jelinek, et al. (2002). Fractop: a tool
for automated biological image classification. 6th AI
Australasia-Japan Joint Workshop, Australian
National University, Canberra.
Jelinek, H. F., A. Karperien, et al. (2004). Differentiating
grades of microglia activation with fractal analysis.
Proceedings of the Complex Systems Conference,
Cairns, Australia, IOS Press.
Jelinek, H. F., A. Karperien, et al. (2002). MicroMod - an
L-systems approach to neuron modelling. 6th AI
Australasia-Japan Joint Workshop, Australian
National University, Canberra.
Karperien, A. (2007). FracLac for ImageJ. FracLac for
ImageJ 2000-2007. Bethesda, Maryland, Research
Services Branch, National Institutes of Health:
Morphological digital image analysis software for
fractal, multifractal, lacunarity, and other
morphometrics.
Kreutzberg, G. W. (1995). "Microglia, the first line of
defence in brain pathologies." Arzneimittelforschung
45(3A): 357-60.
Smith, T. G., W. B. Marks, et al. (1989). "A fractal
analysis of cell images." Journal of Neuroscience
Methods 27: 173-180.
Soltys, Z., O. Orzylowska-Sliwinska, et al. (2005).
"Quantitative morphological study of microglia cells
in the ischaemic rat brain using principle component
analysis." Journal of Neuroscience Methods.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
294
