
TWO-STAGE CLUSTERING OF A HUMAN BRAIN TUMOUR
DATASET USING MANIFOLD LEARNING MODELS
∗
Ra´ul Cruz-Barbosa and Alfredo Vellido
Dept. de Llenguatges i Sistemes Inform`atics, Universitat Polit`ecnica de Catalunya
Edifici Omega, Campus Nord, C. Jordi Girona, 1-3, Barcelona, 08034, Spain
Keywords:
Brain tumours, MRS, Generative Topographic Mapping, two-stage clustering, outliers.
Abstract:
This paper analyzes, through clustering and visualization, Magnetic Resonance spectra of a complex multi-
center human brain tumour dataset. Clustering is performed as a two-stage process, in which the models used
in the first stage are variants of Generative Topographic Mapping (GTM). Class information-enriched variants
of GTM are used to obtain a primary cluster description of the data. The number of clusters used by GTM
is usually large and does not necessarily correspond to the overall class structure. Consequently, in a second
stage, clusters are agglomerated using K-means with different initialization strategies, some of them defined ad
hoc for the GTM models. We evaluate if the use of class information influence the brain tumour cluster-wise
class separability resulting from the process. We also resort to a robust variant of GTM that detects outliers
while effectively minimizing their negative impact in the clustering process.
1 INTRODUCTION
Medical decision making is usually riddled with un-
certainty, especially in sensitive settings such as non-
invasive brain tumour diagnosis. The brain tumour
data analysed in this study are obtained by Magnetic
Resonance Spectroscopy (MRS). Information derived
from the MR spectra can contribute to the evidence
base available for a particular patient, providing sup-
port to clinicians.
The fields of Machine Learning and Statistics co-
exist with data analysis as a common target. An
example can be found in Finite Mixture Models
(Figueiredo and Jain, 2002). In practical scenarios,
such as medical decision making, these models could
benefit from data visualization. Finite Mixture Mod-
els can be endowed with visualization capabilities
provided certain constrains are enforced, such as forc-
ing the mixture components to be centred in a low-
dimensional manifold embedded in the observed data
∗
Alfredo Vellido is a Ram´on y Cajal researcher and
acknowledges funding from the MEC project TIN2006-
08114. Ra´ul Cruz-Barbosa acknowledges SEP-SESIC
(PROMEP program) of M´exico for his PhD grant. Authors
gratefully acknowledge the former INTERPRET project
centres (http://azizu.uab.es/INTERPRET) for making avail-
able and managing the data for this study.
space, as in Generative Topographic Mapping (GTM)
(Bishop et al., 1998), which can be seen as a prob-
abilistic alternative to Self-Organizing Maps (SOM)
(Kohonen, 1995) for data clustering and visualiza-
tion. When available class information can also be
integrated as part of the GTM training to enrich the
cluster structure definition (Cruz and Vellido, 2006).
The resulting models will be used in our experiments
to analyze a complex MRS dataset.
GTM-based models do not place any strong re-
striction on the number of mixture components (or
clusters), in order to achieve an appropriate visual-
ization of the data. This richly detailed cluster struc-
ture does not necessarily match the more global clus-
ter and class structures of the data. In this scenario, a
two-stage clustering procedure may be useful to un-
cover such global structure (Vesanto and Alhoniemi,
2000). GTM and its variants can be used in the first
stage to generate a detailed cluster partition in the
form of a mixture of components. The centres of
these components can be further clustered in the sec-
ond stage. For that role, the well-known K-means al-
gorithm is used in this study.
The first goal of the paper is assessing to what
extent the introduction of class information improves
the final cluster-wise class separation. The issue re-
mains of how we should initialize K-means in the sec-
191
Cruz-Barbosa R. and Vellido A. (2008).
TWO-STAGE CLUSTERING OF A HUMAN BRAIN TUMOUR DATASET USING MANIFOLD LEARNING MODELS.
In Proceedings of the First Inter national Conference on Bio-inspired Systems and Signal Processing, pages 191-196
DOI: 10.5220/0001058501910196
Copyright
c
SciTePress

ond clustering stage. Random initialization (Vesanto
and Alhoniemi, 2000) does not make use of the prior
knowledge generated in the first stage of the proce-
dure and requires a somehow exhaustive search of the
initialization space. Here, we propose two different
ways of introducing such prior knowledge as fixed
initialization. These procedures, resulting from GTM
properties, allow significant computational savings.
In section 2, we summarily introduce the GTM
and its t-GTM and class-enriched variants, as well as
the two-stage clustering procedure with its alternative
initialization strategies. Several experimental results
are provided and discussed in section 3, while a final
section outlines some conclusions.
2 TWO-STAGE CLUSTERING
2.1 The GTM Models
The standard GTM is a non-linear latent variable
model defined as a mapping from a low dimensional
latent space onto the multivariate data space. The
mapping is carried through by a set of basis functions
generating a constrained mixture density distribution.
It is defined as a generalized linear regression model:
y = φ(u)W, (1)
where φ are M basis functions φ(u) =
(φ
1
(u),...,φ
M
(u)). For continuous data of di-
mension D, spherically symmetric Gaussians are an
obvious choice of basis function; W is a matrix of
adaptive weights w
md
that defines the mapping, and
u is a point in latent space. To avoid computational
intractability a regular grid of K points u
k
can be
sampled from the latent space. Each of them, which
can be considered as the representative of a data
cluster, has a fixed prior probability p(u
k
) = 1/K and
is mapped, using (1), into a low dimensional manifold
non-linearly embedded in the data space. This latent
space grid is similar in design and purpose to that
of the visualization space of the SOM. A probability
distribution for the multivariate data X= {x
n
}
N
n=1
can
then be defined, leading to the following expression
for the log-likelihood:
L =
N
∑
n=1
ln
1
K
K
∑
k=1
β
2π
D/2
exp
−βky
k
−x
n
k
2
2
(2)
where y
k
, usually known as reference or prototype
vectors, are obtained for each u
k
using (1); and β is
the inverse of the noise model variance. The EM al-
gorithm is an straightforward alternative to obtain the
Maximum Likelihood (ML) estimates of the adaptive
parameters of the model, namely W and β.
The class-GTM model is an extension of GTM
that makes use of the available class information. The
main goal of this extension is to improve class separa-
bility in the clustering results of GTM. For the Gaus-
sian version of the GTM model (Sun et al., 2002;
Cruz and Vellido, 2006), this entails the calculation
of the posterior probability of a cluster representative
u
k
given the data point x
n
and its class label c
n
, or
class-conditional responsibility ˆz
c
kn
= p(u
k
|x
n
,c
n
), as
part of the E step of the EM algorithm. It can be cal-
culated as:
ˆz
c
kn
=
p(x
n
,c
n
|u
k
)
∑
K
k
′
=1
p(x
n
,c
n
|u
k
′
)
=
p(x
n
|u
k
)p(c
n
|u
k
)
∑
K
k
′
=1
p(x
n
|u
k
′
)p(c
n
|u
k
′
)
=
p(x
n
|u
k
)p(u
k
|c
n
)
∑
K
k
′
=1
p(x
n
|u
k
′
)p(u
k
′
|c
n
)
,
(3)
and, being T
i
each class,
p(u
k
|T
i
)=
∑
n;c
n
=T
i
p(x
n
|u
k
)
∑
n
p(x
n
|u
k
)
∑
k
′
∑
n;c
n
=T
i
p(x
n
|u
k
′
)
∑
n
p(x
n
|u
k
′
)
(4)
The rest of the model’s parameters are estimated fol-
lowing the standard EM procedure.
For the Gaussian GTM, the presence of outliers is
likely to negatively bias the estimation of the adaptive
parameters, distorting the clustering results. In order
to overcome this limitation, the GTM was recently re-
defined (Vellido, 2006; Vellido and Lisboa, 2006) as a
constrained mixture of Student’s t distributions: the t-
GTM, aiming to increase the robustness of the model
towards outliers. The mapping described by Equation
(1) remains, with the basis functions now being Stu-
dent’s t distributions and leading to the definition of
the following mixture density:
p(x|W,β,ν
k
)=
1
K
∑
K
k=1
Γ(
ν
k
+D
2
)β
D/2
Γ(
ν
k
2
)(ν
k
π)
D/2
(1+
β
ν
k
ky
k
−x
n
k
2
)
ν
k
+D
2
(5)
where Γ(·) is the gamma function and the parame-
ter ν = (ν
1
,... ,ν
K
) represents the degrees of free-
dom for each component k of the mixture, so that it
can be viewed as a tuner that adapts the level of ro-
bustness (divergence from normality) for each com-
ponent. This density leads to the redefinition of the
model log-likelihood and, again, the estimation of the
correspondingadaptiveparameters using EM. The ex-
tension to class-t-GTM is straightforward and is omit-
ted here for the sake of brevity.
2.2 Two-Stage Clustering based on
GTM
In the first stage of the proposed two-stage cluster-
ing procedure, the GTM models are trained to ob-
tain the representative prototypes (detailed clustering)
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
192

of the observed dataset. In this study, the resulting
prototypes y
k
of the GTM models are further clus-
tered using the K-means algorithm. In a similar two-
stage procedure to the one described in (Vesanto and
Alhoniemi, 2000), based on SOM, the second stage
K-means initialization in this study is first randomly
replicated 100 times, subsequently choosing the best
available result, which is the one that minimizes the
error function E =
∑
C
c=1
∑
x∈G
c
kx− µ
c
k
2
, where C is
the final number of clusters in the second stage and
µ
c
is the centre of the K-means cluster G
c
. This ap-
proach seems somehow wasteful, though, as the use
of GTM instead of SOM can provide us with richer a
priori information to be used for fixing the K-means
initialization in the second stage.
Two novel fixed initialization strategies that use
the prior knowledge obtained by GTM in the first
stage are proposed. They are based on the Magni-
fication Factors (MF) and the Cumulative Responsi-
bility (CR). The MF measure the level of stretching
that the mapping undergoes from the latent to the data
spaces. Areas of low data density correspond to high
distorsions of the mapping (high MF), whereas areas
of high data density correspond to low MF. The MF
is described in terms of the derivatives of the basis
functions φ
j
(u) in the form:
dA
′
dA
= det
1/2
ψ
T
W
T
Wψ
, (6)
where ψ has elements ψ
ji
= ∂φ
j
/∂u
i
(Bishop et al.,
1997) and dA
′
and dA are, in turn, infinitesimal rect-
angles in the manifold and latent spaces. If we choose
C to be the final number of clusters for K-means in
the second stage, the first proposed fixed initialization
strategy will consist on the selection of the class-GTM
prototypes corresponding to the C non-contiguous la-
tent points with lowest MF for K-means initialization.
That way, the second stage algorithm is meant to start
from the areas of highest data density.
The CR is the sum of responsibilities over all data
points in X for each cluster k:
CR
k
=
N
∑
n=1
ˆz
c
kn
(7)
The second proposed fixed initialization strategy,
based on CR, is similar in spirit to that based on MF.
Again, if we choose C to be the final number of clus-
ters for K-means in the second stage, the fixed ini-
tialization strategy will now consist on the selection
of the GTM prototypes corresponding to the C non-
contiguous latent points with highest CR. That is, the
second stage is meant to start from those prototypes
that are found in the first stage to be most responsible
for the generation of the observed data.
3 EXPERIMENTS
3.1 Human Brain Tumour Data
The multi-center data used in this study consists of
217 single voxel PROBE (PROton Brain Exam sys-
tem) MR spectra acquired in vivo for six brain tumour
types: meningiomas (58 cases), glioblastomas (86),
metastases (38), astrocytomas (22), oligoastrocy-
tomas (6), and oligodendrogliomas (7). For the analy-
ses, the spectra were grouped into three types (typol-
ogy that will be used in this study as class informa-
tion), as in (Tate et al., 2006): high grade malignant
(metastases and glioblastomas), low grade gliomas
(astrocytomas, oligodendrogliomas and oligoastrocy-
tomas) and meningiomas. The clinically relevant re-
gions of the spectra were sampled to obtain 200 fre-
quency intensity values. The high dimensionality of
the problem was compounded by the small number of
spectra available, which is commonplace in MRS data
analysis.
3.2 Experimental Design and Settings
The GTM, t-GTM and their class-enriched counter-
parts were implemented in MATLAB
R
. For the
experiments reported next, the adaptive matrix W
was initialized, following a PCA-based procedure de-
scribed in (Bishop et al., 1998). This ensures the
replicability of the results. The grid of latent points
u
k
was fixed to a square 20x20 layout for the MRS
dataset. The corresponding grid of basis functions φ
was equally fixed to a 5x5 square layout.
The goals of these experiments are fourfold. First,
we aim to assess whether the inclusion of class infor-
mation in the first stage of the procedure results in any
improvement in terms of cluster-wise class separabil-
ity (and under what circumstances) compared to the
procedure using standard GTM. Second, we aim to
assess whether the two-stage procedure improves, in
the same terms, on the use of direct clustering of the
data using K-means. Third, we aim to test whether the
second stage initialization procedures based on MF
and the CR of the class-GTM, described in section
2.2, retain the cluster-wise class separability capabil-
ities of the two-stage clustering procedure in which
K-means is randomly initialized. In fourth place, we
aim to explore the properties of the structure of the
dataset concerning atypical data. For that, we use the
t-GTM (Vellido, 2006), as described in section 2.1.
The clustering results of all models will be first
compared visually, which should help to illustrate the
visualization capabilities of the models. Beyond the
visual exploration, the second stage clustering results
TWO-STAGE CLUSTERING OF A HUMAN BRAIN TUMOUR DATASET USING MANIFOLD LEARNING
MODELS
193
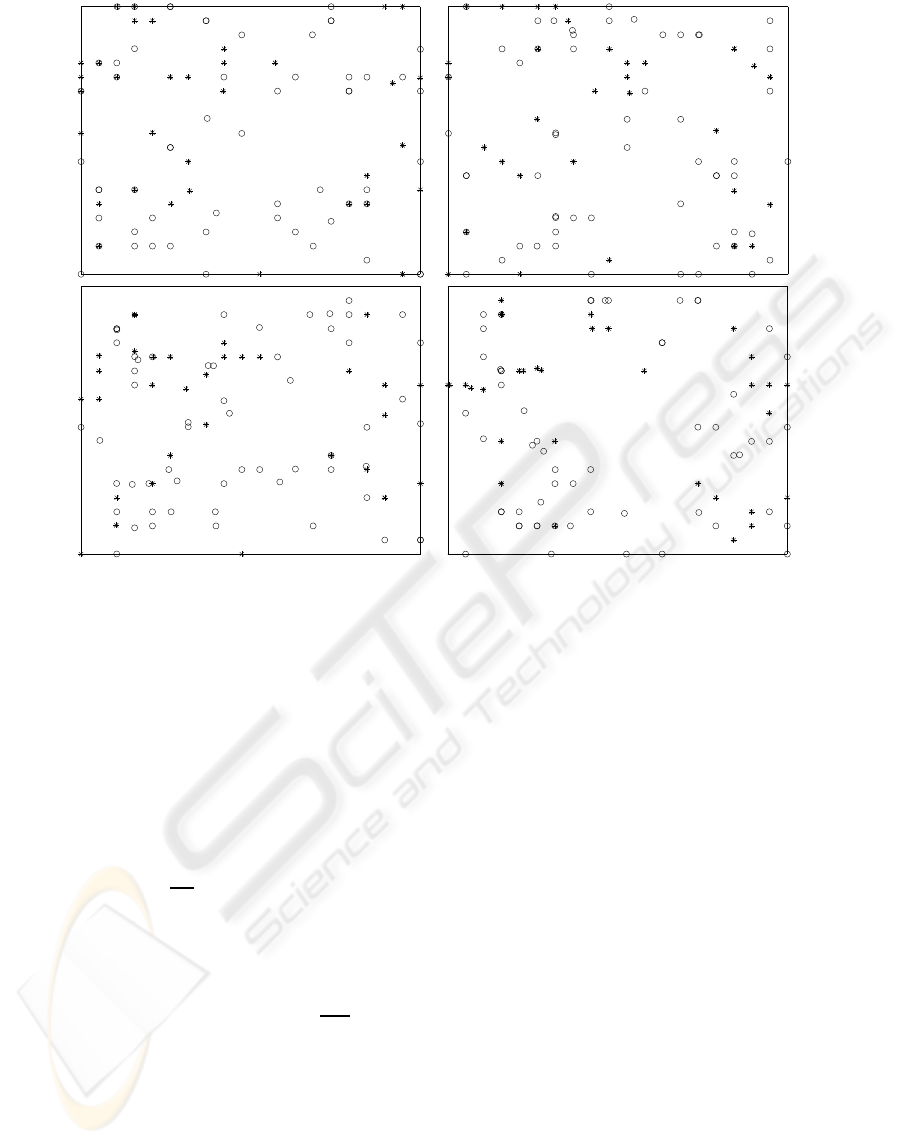
Figure 1: Representation, on the 2-dimensional latent space of GTM and its variants, of a part of the tumour dataset. It is
based on the mean posterior distributions for the data points belonging to low grade gliomas (‘*’) and meningiomas (‘o’). The
axes of the plot convey no meaning by themselves and are kept unlabeled. (Top left): GTM without class information. (Top
right): class-GTM. (Bottom left): t-GTM without class information. (Bottom right): class-t-GTM.
should be explicitly quantified in terms of cluster-
wise class separability. For that purpose, the follow-
ing entropy-like measure is proposed:
E
G
c
({T
i
})= −
∑
{G
c
}
P(G
c
)
∑
{T
i
}
P(T
i
|G
c
)lnP(T
i
|G
c
)
= −
C
∑
c=1
K
G
c
K
|{T
i
}|
∑
i=1
p
ci
ln p
ci
(8)
Sums are performed over the set of classes (tumour
types) {T
i
} and the K-means clusters {G
c
}; K is the
total number of prototypes; K
G
c
is the number of pro-
totypes assigned to the c
th
cluster; p
ci
=
K
G
c
i
K
G
c
, where
K
G
c
i
is the number of prototypes from class i assigned
to cluster c; and, finally, |{T
i
}| is the cardinality of the
set of classes. An entropy of 0 corresponds to the case
of no clusters being assigned prototypes correspond-
ing to more than one class.
Given that the use of a second stage in the cluster-
ing procedure is intended to provide final clusters that
best reflect the overall structure of the data, the prob-
lem remains of what is the most adequate number of
clusters. In this paper we do not use any cluster va-
lidity index and we just evaluate the entropy measure
for solutions from 2 up to 10 clusters.
3.3 Results and Discussion
In the first stage of the two-stage clustering procedure,
GTM, t-GTM and their class-enriched variants class-
GTM and class-t-GTM were trained to model the hu-
man brain tumour dataset. The resulting prototypes y
k
were then clustered in the second stage using the K-
means algorithm. This last stage was performed with
three different initializations, as described in section
2.2. In all cases, K-means was forced to yield a given
number of final clusters, from 2 up to 10. The entropy
was calculated for all settings.
Before considering the entropy results, visualiza-
tion maps (obtained using the mean of the poste-
rior distribution:
∑
K
k=1
u
k
ˆz
kn
or
∑
K
k=1
u
k
ˆz
c
kn
) of all the
trained models in the first stage were generated. Three
hypotheses were made for the clustering results vi-
sualized here. First, the use of class information
in the clustering models should yield visualization
maps where classes are separated better than in those
models which do not use it. Second, the use of t-
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
194
GTM should help to diminish the influence of out-
liers and the visualization maps generated with these
models should show the data more homogeneously
distributed throughout the visualization maps than in
Gaussian GTM, which do no use it. Thirdly, since
the tumour dataset is stronly class-unbalanced, we hy-
pothesized that the small classes would consist mainly
of atypical data. The second and third hypotheses will
be tested using the t-GTM variants.
For the sake of brevity, we only provide one of
these illustrative visualizations in Fig. 1.
Here, two tumour groups (low grade gliomas and
meningiomas) are shown. The right column of Fig.
1, where the models that include class information
are located, provides some preliminary support for
the first hypothesis since the class separation between
both classes is better than that of the models that
do not use class information, located in the left col-
umn. This can be observed in the form of a more pro-
nounced overlapping of both classes in the left hand-
side models of Fig. 1. This is reinforced by the en-
tropy results provided later on in the paper.
The use of t distributions in the models repre-
sented in the bottom row yields a similar data spread
to that of the standard Gaussian GTM models of the
top row. This is an indication that there might be not
too many clear outliers in the two classes visually rep-
resented. Therefore, the second hypothesis cannot be
supported at this stage.
We now turn our attention to the third hypothe-
sis. In (Vellido and Lisboa, 2006) it was shown that a
given data instance could be characterized as an out-
lier if the value of
O
∗
n
=
∑
k
ˆz
kn
βky
k
− x
n
k
2
(9)
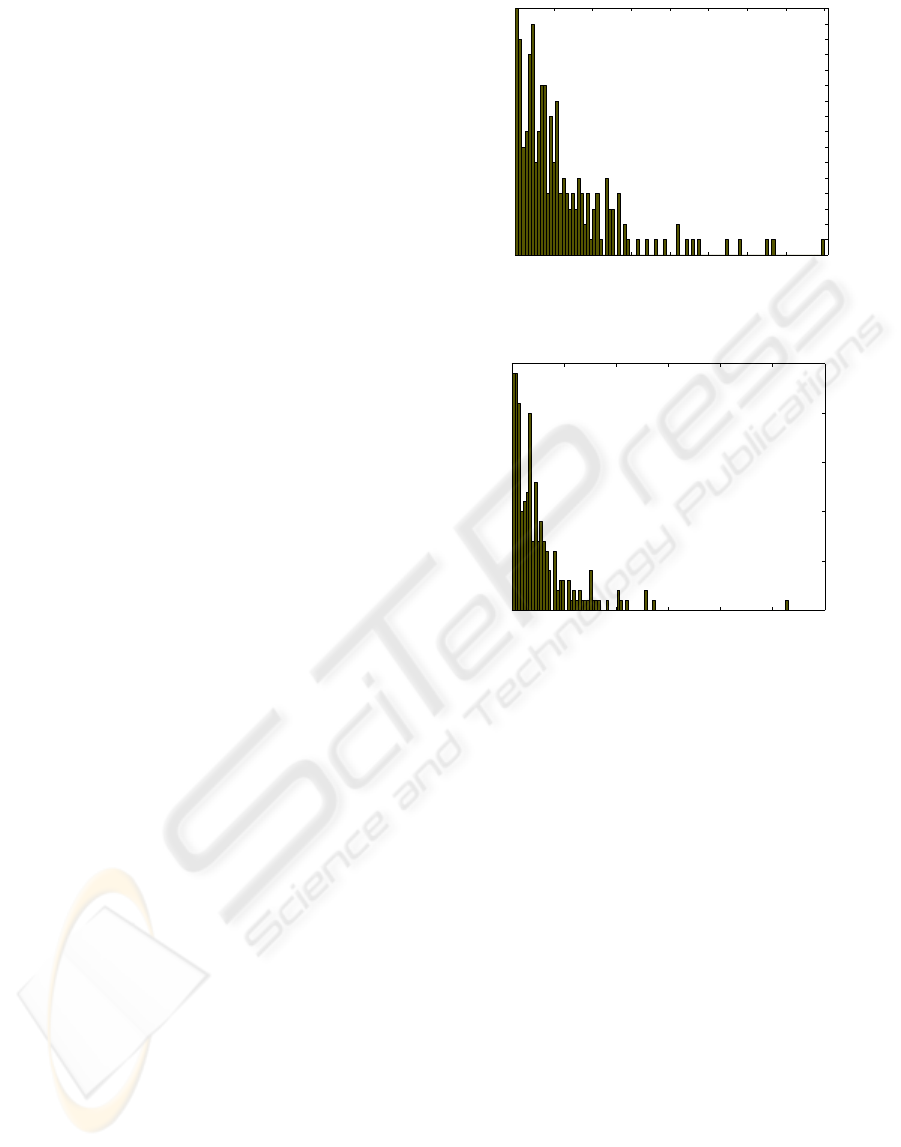
was sufficiently large. The histogram in Fig. 2 dis-
plays the values of O
∗
n
from (9) for the brain tumour
dataset. We did the same for the class-t-GTM model
and the corresponding values of O
∗
n
are displayed in
Fig. 3.
First of all, and supporting our previous impres-
sion, not too many data could be clearly characterized
as outliers according to these histograms. Somehow
surprisingly, given the complex tumour typology of
the dataset under study, these results do not support
the third hypothesis, as most of the spectra that might
be considered as outliers actually belong to the largest
and best represented tumour types, such as menin-
giomas and glioblastomas. Interestingly, few metas-
tases and astrocytomas are amongst the most extreme
outliers.
The entropy measurements quantifying the
cluster-wise class separation for the brain tumour
dataset are shown in Fig. 4. Two immediate conclu-
0 200 400 600 800 1000 1200 1400 1600
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
−−−−−meningioma
−−−−−−−−−−glioblastoma
−−−−−−−−−−−−−−−−−−−−−−astrocytoma
−−−glioblastoma, metastases
−−−−−meningioma
−−−−−−−−−−glioblastoma
−−−−−meningioma
−−−glioblastoma
−−−glioblastoma
Figure 2: Histogram of the statistic (9) for the t-GTM
model; outliers are characterized by its large values. As
an example, the ten largest values are labeled.
0 500 1000 1500 2000 2500 3000
0
5
10
15
20
25
−−−−glioblastoma
−−−−meningioma
−−−−astrocytoma
−−−−meningioma
Figure 3: Histogram of (9) for class-t-GTM. As an example,
the four largest values are labeled.
sions can be drawn: First, all the two-stage clustering
procedures based on GTM perform much better than
the direct clustering of the data through K-means in
terms of cluster-wise class separation. The two-stage
procedure based on class-GTM also performs much
better than its counterpart without class information
based on the standard GTM (right hand side of Fig.
4). On the contrary, it can also be observed that
the two-stage clustering based on class-t-GTM does
not perform better than the t-GTM model. This
is explained by the fact that the adjustment of the
model provided by t-GTM, which is blind to class
information by itself, alters the accordance between
class and cluster distributions, especially in a strongly
class-unbalanced dataset such as the one under
analysis. This result draws the limits out of which the
addition of class information is not necessarily useful
in terms of cluster-wise separation. The second
main conclusion to be drawn is that the random
initialization in the second stage of the clustering
procedure, with or without class information, does
not entail any significant advantage over the proposed
fixed initialization strategies across the whole range
of possible final number of clusters, while being far
more costly in computational terms.
TWO-STAGE CLUSTERING OF A HUMAN BRAIN TUMOUR DATASET USING MANIFOLD LEARNING
MODELS
195

1 2 3 4 5 6 7 8 9 10
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
clusters
entropy
km alone
rand init−c
MF init−c
CR init−c
rand init−nc
MF init−nc
CR init−nc
rand init−ct
MF init−ct
CR init−ct
rand init−nct
MF init−nct
CR init−nct
1 2 3 4 5 6 7 8 9 10
0.17
0.175
0.18
0.185
0.19
0.195
0.2
0.205
clusters
entropy
rand init−c
MF init−c
CR init−c
rand init−nc
MF init−nc
CR init−nc
rand init−ct
MF init−ct
CR init−ct
rand init−nct
MF init−nct
CR init−nct
Figure 4: Entropy for the two-stage clustering of the tumour dataset, with different initializations (MF init, CR init and rand
init) and K-means alone. The ‘c’ and ‘nc’ symbols refer to models that, in turn, use and not use class information. The ‘t’ in
the legend means that t-GTM was used in the first stage. (Left): all models are shown. (Right): only the GTM, t-GTM and
their class-enriched variants are shown.
The entropy measure in (8) quantifies the level
of agreement between the clustering solutions and
the class distributions. In terms of the overall
cluster-wise class separation provided by the Gaus-
sian distributions-based GTM clustering models, it
has been shown that the addition of class information
consistently helps. As a result, these class-enriched
models would be useful in a semi-supervised setting
in which new undiagnosed tumour cases were added
to the database.
4 CONCLUSIONS
In this paper we have analyzed the influence exerted
by the inclusion of class information in the two-stage
clustering of a complex human brain tumour MRS
dataset. We have also introduced two economical and
principled fixed initialization procedures for the sec-
ond stage of the procedure. The existence of atypi-
cal data or outliers in the human brain tumours MRS
dataset under study and its influence on the clustering
have also been explored.
REFERENCES
Bishop, C. M., , Svens´en, M., and Williams, C. K. I. (1997).
Magnification Factors for the GTM algorithm. In
Proceedings of the IEE fifth International Conference
on Artificial Neural Networks, pages 64–69.
Bishop, C. M., Svens´en, M., and Williams, C. K. I. (1998).
The Generative Topographic Mapping. Neural Com-
putation, 10(1):215–234.
Cruz, R. and Vellido, A. (2006). On the improvement of
brain tumour data clustering using class information.
In Proceedings of the 3rd European Starting AI Re-
searcher Symposium (STAIRS’06), Riva del Garda,
Italy.
Figueiredo, M. A. T. and Jain, A. K. (2002). Unsuper-
vised learning of finite mixture models. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
24(3):381–396.
Kohonen, T. (1995). Self-Organizing Maps. Springer-
Verlag, Berlin.
Sun, Y., Tiˇno, P., and Nabney, I. T. (2002). Visualization of
incomplete data using class information constraints.
In Winkler, J. and Niranjan, M., editors, Uncertainty
in Geometric Computations, pages 165–174. Kluwer
Academic Publishers, The Netherlands.
Tate, A. R., Underwood, J., Acosta, D. M., Juli`a-Sap´e, M.,
Maj´os, C., Moreno-Torres, A., Howe, F. A., van der
Graaf, M., Lefournier, V., Murphy, M. M., Loose-
more, A., Ladroue, C., Wesseling, P., Bosson, J. L.,
Caba˜nas, M. E., Simonetti, A. W., Gajewicz, W., Cal-
var, J., Capdevila, A., Wilkins, P. R., Bell, B. A.,
R´emy, C., Heerschap, A., Watson, D., Griffiths, J. R.,
and Ar´us, C. (2006). Development of a decision sup-
port system for diagnosis and grading of brain tu-
mours using in vivo magnetic resonance single voxel
spectra. NMR in Biomedicine, 19:411–434.
Vellido, A. (2006). Missing data imputation through GTM
as a mixture of t-distributions. Neural Networks,
19(10):1624–1635.
Vellido, A. and Lisboa, P. J. G. (2006). Handling out-
liers in brain tumour MRS data analysis through ro-
bust topographic mapping. Computers in Biology and
Medicine, 36(10):1049–1063.
Vesanto, J. and Alhoniemi, E. (2000). Clustering of the
Self-Organizing Map. IEEE Transactions on Neural
Networks, 11(3):586–600.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
196
