
XML INDEX COMPRESSION BY DTD SUBTRACTION
Stefan Böttcher, Rita Steinmetz
Computer Science, University of Paderborn, Fürstenallee 11, 33102 Paderborn, Germany
Niklas Klein
ComTec, University of Kassel, Wilhelmshöher Allee 73, 34121 Kassel, Germany
Keywords: XML, Compression, Index, Data Streams.
Abstract: Whenever XML is used as format to exchange large amounts of data or even for data streams, the verbose
behaviour of XML is one of the bottlenecks. While compression of XML data seems to be a way out, it is
essential for a variety of applications that the compression result can be queried efficiently. Furthermore, for
efficient path query evaluation, an index is desired, which usually generates an additional data structure. For
this purpose, we have developed a compression technique that uses structure information found in the DTD
to perform a structure-preserving compression of XML data and provides a compression of an index that
allows for efficient search in the compressed data. Our evaluation shows that compression factors which are
close to gzip are possible, whereas the structural part of XML files can be compressed even better.
1 INTRODUCTION
1.1 Motivation
XML is widely used as a data exchange standard and
DTDs are one of the key concepts to ensure
correctness of XML data. While the structural
information contained in XML trees is considered
being one of the strengths of XML, it has the
following disadvantages: structure makes XML files
rather verbose compared to the text values enclosed
in the structures of an XML file.
Whenever the structure of an XML document is
defined by a DTD, we can take advantage of the fact
that the DTD defines some structure patterns that
occur repeatedly in the XML document. The key
idea of our structure preserving compression is to
compress the verbose structural parts of XML
documents that are redundant when regarding the
structure of a given DTD. In order to be able to
construct an index for path queries, our structure
preserving data format separates a compressed
structure index, called kleene size tree (KST) from
the compressed data values of the XML document.
Our paper has the following contributions:
1. From the DTD, we derive a set of grammar
rules that can be used for the following: to compress
the structural part of the XML data to a structure
preserving kleene size tree (KST) and a data format
called constant XML stream (CXML) to store the
text constants and attribute values of XML
documents.
2. The same grammar rules can be used to
decompress the generated data structures KST and
CXML back to the XML data given before.
3. The kleene size tree (KST) can be used for
transforming path-oriented search operations on an
XML document to equivalent queries on the con-
stant XML (CXML) stream.
4. We have evaluated our approach and show that
significant compression of the XML structure is
possible. Our experiments have shown that the size
of the KST is on average only 3.6% of the size of the
structure of the original XML file.
Our approach – which we call DTD subtraction -
is especially useful, when the structure of the XML
document is the bottleneck of the data exchange.
Finally, our approach can be used for extremely
large XML documents and it supports streaming of
XML documents.
DTD subtraction can be summarized as follows.
We represent each element declaration of a given
DTD as both a syntax tree and a set of grammar
rules (Section 2). The set of grammar rules is then
augmented to an attribute grammar for either
compression of an XML document to a KST and a
CXML stream, for decompression of a KST and a
86
Böttcher S., Steinmetz R. and Klein N. (2007).
XML INDEX COMPRESSION BY DTD SUBTRACTION.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - DISI, pages 86-94
DOI: 10.5220/0002365900860094
Copyright
c
SciTePress

CXML stream or for transforming path queries on
the XML data into queries on CXML data and an
index generated from the KST (Section 3). Section 4
outlines how our approach can be extended to
arbitrary DTDs and to XML streams. Section 5
summarizes our experimental results, whereas
Section 6 discusses related works and Section 7
outlines the summary and conclusions.
2 TRANSFORMING A DTD INTO
A SET OF GRAMMAR RULES
2.1 Element Declarations
For simplicity of the presentation, we consider
DTDs containing only element declarations. For
example, the element declaration
< !ELEMENT E1 ( E2 , ( E3|E4 ) )* >
defines each element E1 to enclose an arbitrary
number of sequences each of which consists of the
element E2 followed by either an element E3 or an
element E4. We call (E2, (E3|E4))* the right hand
side of the element declaration. This right hand side
applies the kleene operator (*) to the sequence
operator (,) which itself is applied to the child
element E2 of E1 and the choice operator (|) that
itself is applied to the child elements E3 and E4 of
E1.
In comparison, an element declaration
< !ELEMENT E2 ( #PCDATA ) >
defines the element E2 to contain only PCDATA. In
this case, the right-hand side of the element
declaration contains only the expression #PCDATA.
In general, each right hand of an element
declaration can be regarded as a regular expression
which combines zero or more child elements or the
#PCDATA entry or the EMPTY entry by using the
operators sequence (,), choice (|) or kleene(*). Note
that the (+) operator found in element declarations
can always be expressed by using the sequence and
kleene operators, i.e., we replace (E) + with (E,
(E*)). Similarly, the option operator (?) can be
expressed by using choice and EMPTY, i.e., we
replace (E?) with (E|EMPTY). Furthermore, an
extension of our approach to attributes is straight
forward, i.e., a list of attributes defined in an
ATTLIST declaration for an element E can be
treated similar to a sequence of child elements of E
where optional attributes are treated like optional
elements. In order to keep the following discussion
simple, we only talk about elements and do not
explicitly mention attributes.
We exclude however the ANY operator from
DTD element declarations because the ANY
operator does not allow us to infer the type
information that we need.
2.2 Representing Element Declarations
as Syntax Trees
Grammar rules for compression and XML path
query translation are generated from the element
declarations of the DTD. For this purpose, each
element declaration is parsed and transformed into a
binary syntax tree consisting of 7 types of element
declaration nodes. Some node types have a
parameter. For example, the element declarations
given in the previous section are represented by the
syntax trees given in Figure 1:
element_decl( E1 ) element_decl( E2 )
| |
kleene (N0) pcdata
|
sequence (N1)
/ \
child_element( E2 ) choice (N2)
/ \
child_element( E3 ) child_element( E4 )
Figure 1: Syntax trees of the element declarations given in
Section 2.1. Unique node IDs (N0, N1, N2) are generated
for inner nodes.
In general, there are the following 7 element
declaration node types which are used in syntax
trees:
1. element_decl( Element name ). A node of this
type is generated for each element defined in an
element declaration. The name of the defined
element is passed as a parameter. Each element_decl
node has exactly one successor node which is the
root of the sub-tree representing the right hand side
of the element declaration.
2. child_element( Element name ). A node of this
type is generated for each occurrence of an element
in the right hand side of an element declaration. The
name of this element is passed as a parameter. Each
child element definition has no successor nodes in
the syntax tree.
3. pcdata. The pcdata node is used whenever the
right-hand side of an element declaration contains
the string ‘#PCDATA’. The pcdata node does not
have a parameter, and it does not have a successor
node in the syntax tree.
4. sequence. A node of type sequence is generated
for each sequence operator (,) occurring in the right
hand side of an element declaration. A sequence
node does not have a parameter. Each sequence node
has two successor nodes representing the two
arguments of this sequence operator (,) in the
element declaration.
XML INDEX COMPRESSION BY DTD SUBTRACTION
87

5. choice. A node of type choice is generated for
each choice operator (|) occurring in the right hand
side of an element declaration. A choice node does
not have a parameter. Each choice node has two
successor nodes representing the two arguments of
this choice operator (|) in the element declaration.
6. kleene. A node of type kleene is generated for
each kleene operator (*) occurring in the right hand
side of an element declaration. A kleene node does
not have a parameter. Each kleene node has one
successor node representing the argument of this
kleene operator (*) in the element declaration.
7. empty. A node of type empty is generated for
each string ‘EMPTY’ occurring in an element
declaration. Nodes of type empty do neither have a
parameter nor a successor node in the syntax tree.
Each element declaration is parsed and translated
into a syntax tree, each node of which has exactly
one of the 7 node types described above.
2.3 Determining a Set of Starting
Terminal Symbols
As a final step of parsing an element declaration, we
collect the set of starting terminal symbols for each
node except the root node of the element declaration
syntax tree. These sets of starting terminal symbols
allow the parser to decide during parsing, which
grammar rule has to be applied. The set of starting
terminal symbols (STS) can be computed by the
following rules:
STS(child_element(name)) := { name }
STS(pcdata) := { pcdata }
STS(empty) := { empty }
STS(sequence(a,b)):=STS(a), if empty ∉ STS(a)
STS(sequence(a,b)):=STS(a)∪STS(b),
if empty ∈ STS(a)
STS(choice(a,b)) := STS(a) ∪ STS(b)
STS(kleene(a)) := { empty } ∪ STS(a)
For the following presentation in Section 2 and
Section 3, we assume that the sets of starting
terminal symbols of two sibling nodes that follow a
choice node are always disjoint, such that the current
context node found in the input XML document
uniquely determines which choice has to be taken.
This is a legitimate assumption, as the determinism
of XML content models is a non-normative
constraint of the XML specification ((XML, 2000),
Appendix E).
2.4 Rewriting Element Declaration
Syntax Trees into Grammar Rules
For each inner node i occurring in an element
declaration syntax tree, we generate a unique node
ID, Ni, and for each node type, we generate its own
grammar rule set. As there are 7 types of nodes
occurring in an element declaration syntax tree, we
get 7 different types of grammar rule sets, i.e., one
set of grammar rules for each element declaration
node type. In order to distinguish the rules generated
for different nodes of the same type, we
parameterize the rules with node IDs, Ni, associated
with each node in the element declaration syntax
tree. A further parameter occurring in the rules
generated for nodes of the types sequence, choice, or
kleene is the set of starting terminal symbols
computed for that node. Finally, the rules for
element_decl nodes contain the element to be de-
fined as a parameter, and whenever child_element
nodes occur in the syntax tree as a node referenced
by a parent node P, the grammar rule defined for P
contains a ‘child_element’ call with the child
element found in the element declaration syntax tree
as a parameter.
For example, the grammar rule sets generated for
the syntax trees of Figure 1 are:
element_decl( E1 ) Æ kleene( N0, {E2} ) .
kleene( N0, {E2} ) Æ sequence( N1, {E2} ).
sequence( N1, {E2} ) Æ child_element( E2 ) ,
choice( N2, {E3,E4} ) .
choice( N2, {E3,E4} ) Æ child_element( E3 ) .
choice( N2, {E3,E4} ) Æ child_element( E4 ) .
element_decl( E2 ) Æ pcdata.
pcdata Æ .
3 USING THE GRAMMAR RULE
SET FOR COMPRESSION AND
INDEX CREATION
3.1 Using the Grammar Rule Set for
Compression
The goal of our compression algorithm is to generate
the kleene size tree (KST), i.e., a tree that contains
only that part of the XML document which is not
pre-defined by the DTD. The KST can be regarded
as a compression of the structure of the XML
document. However, it can also be used to generate
an index for efficient access to the XML document.
Each node in the KST stores a value representing a
concrete XML fragment where the DTD allows for
several options, i.e., which choice is taken at a
certain node of the XML document for which a
choice operator (|) in the DTD allows different
options, and how many times a child node or a group
of child nodes is repeated in a certain fragment of
ICEIS 2007 - International Conference on Enterprise Information Systems
88

the XML document where the DTD uses the kleene
operator (*) to allow an arbitrary number.
The grammar rule set can be used for
compression by augmenting it to an attribute
grammar, i.e., by adding attributes that perform
compression as follows. We use the Definite Clause
Grammar (DCG) rule notation of Prolog (Closkin,
1997) to describe the implementation of the attribute
grammar rules, and we use the notation
“[Input]/[OutputKst]” in order to describe that Input
has to be read or consumed from the XML input file
or XML input data stream, and OutputKst has to be
written to the KST. Furthermore, parenthesis, {.},
are used in DCG rules to describe side-effects or
conditions that have to be true if a DCG rule is
applied. How each grammar rule is augmented
depends on the rule head, i.e., on the node type
represented by the rule.
Before we describe the general augmentation of
grammar rules, we start with an example. The rule
element_decl(E1) Æ sequence( N1, {E2} ).
is augmented to
element_decl(E1)Æ [E1]/[], sequence(N1,{E2} ).
The empty pair of brackets, [ ], indicates that
nothing is written to the KST. Therefore, the
augmented grammar rule can be read as follows:
consume an opening E1 element tag from the input,
output nothing to the KST file and continue with
applying the sequence grammar rule that matches
the node ID N1.
The augmentation technique is the same in the
general case, i.e., each grammar rule
element_decl( E ) Æ right hand side .
is augmented to
element_decl( E ) Æ [E] / [ ] , right hand side.
Grammar rules for sequence node types are not
augmented, i.e., they remain as they are, e.g.
sequence( N1, {E2} ) Æ child_element( E2 ) ,
choice( N2, {E3,E4} ).
or in general they remain:
sequence( Ni, S ) Æ right hand side.
Grammar rules for choice node types occur
whenever the DTD allows two different options.
Therefore, grammar rules for choice node types are
augmented with checking which input element is the
next on the input stream, and they write the choice
taken, i.e., whether it is the first or the second choice
that is allowed by the DTD, to the KST. Within the
example, the grammar rules
choice( N2, {E3, E4} ) Æ child_element( E3 ) .
choice( N2, {E3, E4} ) Æ child_element( E4 ) .
are augmented to the following grammar rules
choice( N2, {E3, E4 } ) Æ {next tag ∈ {E3}} ,
[ ] / [1] , child_element( E3 ) .
choice( N2, {E4, E4} ) Æ {next tag ∉ {E3}} ,
[ ] / [2] , child_element( E4 ) .
Within these augmented rules, the output [1] (or
[2]) written on the KST expresses that the first (or
second) choice described by the DTD has been
taken. We write this information to the KST in order
to be able to reconstruct the original XML data from
the KST and the CXML file.
In general, the choice operator may not only
combine elements, but may combine two
expressions. Then, each pair of grammar rules for a
choice operator taking a node ID Ni and two sets
STS1 and STS2 of starting terminal symbols as
parameters
choice(Ni, (STS1∪STS2) )
Æ right hand side 1.
choice(Ni, (STS1∪STS2) ) Æ right hand side 2.
is replaced with the following pair of grammar rules:
choice(Ni, (STS1∪STS2))Æ{next tag ∈ STS1 }
[ ] / [ 1 ], right hand side 1.
choice(Ni, (STS1∪STS2))Æ{next tag ∉ STS1 }
[ ] / [ 2 ], right hand side 2.
child_element calls in a grammar rule simply call
the element grammar rule for the element given as
the parameter.
child_element( E ) Æ element_decl( E ).
Finally, grammar rules for kleene node types are
replaced with a set of augmented grammar rules that
count the arguments taken by a kleene operator
within the CXML stream. Within the example, the
grammar rule
kleene( N0, {E2} ) Æ sequence( N1, {E2} ).
is replaced with the following grammar rules
kleene( N0, {E2} ) Æ [ ] / [ Count ] ,
repeat( N0, {E2} , Count ) .
repeat( N0, {E2}, Count ) Æ {next tag∈{E2}},
sequence(N1,{E2}), repeat(N0,{E2},
Count1 ) , { Count is Count1+1 }.
repeat( N0, {E2}, 0 ) Æ { next tag∉{E2} } .
Here, the repeat rules count how often the argument
of the kleene operator (*) occurs and the kleene rule
writes the Count value into the KST
In general, each given grammar rule for a kleene
operator taking a node ID Ni and a set S of starting
terminals as parameters
kleene( Ni, S ) Æ right hand side .
is replaced with the following new grammar rules
kleene(Ni, S) Æ[]/[Count], repeat(Ni, S, Count).
repeat(Ni, S, Count) Æ {next tag ∈ S},
right hand side , repeat( Ni, S, Count1 ) ,
{ Count is Count1+1 } .
repeat( Ni, S, 0 ) Æ { next tag ∉ S } .
The variable Count in the new grammar rules counts
how often the first repeat grammar rule is executed,
i.e., how often the sub-tree described by the right
hand side of the given kleene grammar rule is
repeated. This number of repetitions will be used in
XML INDEX COMPRESSION BY DTD SUBTRACTION
89

indexing, i.e., translating XML path queries to index
positions for certain data.
3.2 The Constants’ Data Stream
Furthermore, we hash text values in a compressed
data storage model, which allows us to transfer each
constant only once.
pcdata calls simply store the position of each
constant in the CXML stream. A function
positionOf(…) is used to store new constants in the
data storage model, i.e., each constant is stored only
once, and to attach the current position to the
constant. Altogether, the data storage model stores
constants together with a set of positions.
Given the function positionOf(…), the pcdata
grammar rule is implemented as follows:
pcdata()Æ[Constant]/[], {positionOf(Constant)}.
An empty operator can be seen as a text constant
of length 0, and it is treated in a similar way as a
special kind of pcdata, i.e., the function call
positionOf( ) is used for collecting positions of
empty nodes. The only difference is that the empty
operator does not consume or read any input.
empty() Æ { positionOf( ) } .
3.3 The Kleene Size Tree (KST)
Besides compressing the constants in an XML
stream, our goal is to compress a structure-oriented
index, i.e., an index supporting efficient access to
structural information without decompressing all of
the compressed data. The key idea of our index
compressing technique is to use the structure
information provided by element declarations of the
DTD in order to compute the position of certain
elements or text values, such that the compressed
index is much smaller than the structure of the XML
document.
For the DTD rule operators sequence, pcdata,
empty, and child element, a relative position of the
searched data in the data stream can be uniquely
determined by the DTD alone. However, for each
kleene operator (*), the number of repetitions may
vary, and therefore the size of the data elements “in
the scope of” a kleene operator may vary.
Furthermore, for each choice operator (|), the size of
the sub-tree may depend on the choice taken. We
have to store this information somewhere in order to
support loss-less decompression. We write this
information into an index called the kleene size tree
(KST).
The kleene size tree (KST) is organized as
follows: It contains a choice node for each choice
operator (|), and a counter for each kleene operator
(*) that is applied in a DTD rule when parsing the
XML document with the DTD grammar rules. The
hierarchy of the KST nodes corresponds to the
calling hierarchy of DTD element declaration syntax
rules. That is, whenever a rule for a kleene operator
or a choice operator O1 directly or indirectly calls a
rule for a kleene operator or a choice operator O2,
then the KST node K1 representing O1 is an
ancestor of the KST node K2 representing O2.
Note that the KST does not contain any node for
other operators than kleene (*) and choice(|) as all
other operators have a fixed size, i.e., their size can
be computed from the DTD. As the KST contains
only numbers, the KST is a very small data
structure.
Note that the KST is significantly smaller than the
index, i.e., transferring the KST from a sender to a
receiver may be advantageous compared to
transferring an index when bandwidth is a
bottleneck. Furthermore, the KST and CXML file
are not only much smaller than the XML file, but
also allow for a direct access to XML nodes, i.e.,
using the KST for index computations and direct
access to the CXML stream may be advantageous in
scenarios where we can profit from skipping some
XML data.
In order to reconstruct the index, i.e., the structure
of the XML document, from the DTD syntax trees
and the KST, we have to traverse the DTD syntax
trees starting from the root node. Whenever a kleene
node or a choice node is reached, we consume the
next number from the KST and generate the number
of nodes (for kleene nodes) or the node with the
chosen element name of the alternative (for choice
nodes). Note however, that the index does not have
to be reconstructed physically in case of XML path
query evaluation or partial decompression, but it
only needs to be reconstructed ‘virtually’, i.e., only
the positions of the required elements are computed
from DTD and KST, but the index is not
reconstructed physically in order to count the
position. Only in case of a complete decompression,
the index is reconstructed completely, as it is the
major part of the decompressed document.
3.4 Using the Grammar Rules for Path
Queries on Compressed Data
When searching data that matches a certain path of
an XPath expression, we use the KST stream to
identify the position of the information we look for.
Let us extend the previous example and assume
that a given XML input document D has been
compressed to a KST document KD and a CXML
document CD. Furthermore, let us consider that an
ICEIS 2007 - International Conference on Enterprise Information Systems
90

XPath query /E1[2]# asks for the sub-tree enclosed
in the second E1 element contained in the input
stream. Finally, we assume that the first E1 element
has 10 sequences, whereas 3 of them contain an E3
element and 7 of them contain an E4 element and
the second E1 element has 5 sequences, whereas 4
of them contain E3 and one contains E4. This
information is read from KD. Therefore, we can
compute the size of the subtrees for the first E1
element to be E11size =10*size(E2) + 3*size(E3) +
7*size(E4) and for the second E1 Element to be
E12size=5*size(E2) + 4*size(E3) + 1*size(E4). As
E2 only contains pcdata, we know that size(E2)=1.
We assume furthermore that E3 is a sequence of
three elements with pcdata and E4 contains pcdata
directly, i.e., size(E3)=3 and size(E4)=1. Given
these sizes, the sizes of the compressed
representations of the first two E1 elements are
E11size= 10*1+3*3+7*1=26 and E12size
=5*1+4*3+1*1=18. Altogether, when we query for
/E1[2], we can skip the first E11size bytes from CD
and then read and decompress the next E12size
bytes from CD. Because we know that the fragment
searched for matches the DTD for E1, we know
which decompression grammar rule has to be used,
in this case, the decompression grammar rule for E1.
We explain decompression in the next section.
The general computation of sub-tree sizes extends
the KST with constant size information that can be
derived from the element declaration rules.
However, this computation is only done for paths to
accessed CXML elements.
3.5 Using the Grammar Rule Set for
Decompression
Similarly as for compression, the grammar rule set
can be used for decompression. In our Prolog
implementation this is simply done by switching the
roles of the input stream and the output stream.
More precisely, within a Prolog call
element_decl(Input, OutputKST), the first
parameter, Input, which is the input stream for
compression, will be the output stream for
decompression. Similarly, the second parameter
OutputKST which is the KST output stream for
compression will be an input parameter for
decompression. Within a first prototype, we have
implemented the augmented DCG rule system in
Prolog in such a way that it can be used for both
directions compression and decompression, by either
providing an XML document Inputstream or
providing a CXML document Outputstream and the
KST document Outputstream. For the performance
evaluation, we have re-implemented the grammar
rule system in a different language, i.e., Java using a
SAX parser and the attribute grammar of JavaCC,
and there we had one augmented rule set for
compression, and an additional reverse
implementation for decompression.
4 EXTENDING THE APPROACH
TO XML STREAMS
4.1 Processing XML Streams and
Recursive DTDs
We are not limited to compressing only XML
documents of a fixed size. Instead, we are also able
to compress XML streaming data because we do not
have to read the whole document, before we can
start data compression, i.e., the augmented grammar
rules can be used to compress on the fly.
1
Furthermore, we did not limit our approach to
non-recursive DTDs, i.e., all the same ideas can be
applied, when the element declaration defining E1 is
changed to a recursive element declaration
< !ELEMENT E1 ( E2, ( E1|E4 ) )* >
Therefore, our approach (including index
computation and path evaluation) is also applicable
to recursive DTDs.
4.2 Evaluation of XPath Queries on
Compressed XML Streams
We assume that the XPath expression that is
evaluated does not contain any backward-axes, but
may contain any forward axes, predicate filters and
node name tests (either an element name or the
wildcard ‘*’). If an XPath expression contains
backward-axes, the algorithm presented in (Olteanu,
2002) can be used to rewrite the XPath expression
into an equivalent XPath expression containing no
backward-axes.
For the evaluation of XPath queries, we propose
an adaptation of an approach presented in (Su,
2005). This approach optimizes XPath query
evaluation on XML documents and especially on
data streams, where the whole data has to be read at
most once. The buffer size needed to store elements
temporarily depends on the evaluation of XPath
filters. Furthermore, schema information in the DTD
reduces the computational time needed for deciding
satisfiability of filters and determines parts of the
1
Due to space limitations, we skip some technical details here,
e.g., providing space for very large counters in an index and the
treatment of very large kleene size trees and of very large text
constants.
XML INDEX COMPRESSION BY DTD SUBTRACTION
91
data that can be skipped, as they do not contain any
information needed to determine the answer to the
query. This ‘skipping’ of parts of the data
corresponds to directly addressing the known
position of the next element as proposed in our
approach. The difference however is that we have to
process compressed XML data, i.e., in order to use
the approach presented in (Su, 2005), we have to
translate location steps into position offsets in the
CXML stream.
Which part of the data can be skipped, i.e., the
concrete position-offset from a current position
within the data, can be computed by combining the
size information stored in the KST with offset
information that is computed from the element
declaration syntax trees.
4.3 Multiplexing Stream Data
When considering an XML stream, we have two
kinds of output stream, the CXML data stream and
the KST stream. In a practical implementation
compressing XML streams, we multiplex these two
data streams at the sender’s side, and de-multiplex
the multiplexed stream back into the two streams at
the receiver’s side.
5 EXPERIMENTAL RESULTS
We have implemented our approach using Java 1.5
and a SAXParser for parsing XML data. As
compressed storage model for constant data, we
have chosen a trie (Fredkin, 1960) the inner nodes of
which are compressed using Deflate (LZ77(Ziv,
1977) + Huffmann encoding (Huffmann, 1952)).
Note that the compressed storage model for constant
data can be replaced by any other model that allows
to store and evaluate pairs of positions and values.
We have evaluated our compression approach on
the following datasets:
1. XMark(XM) – an XML document that models
auctions (Schmidt, 2002)
2. hamlet(H) – an XML version of the famous
Shakespeare play
3. catalog-01(C1), catalog-02(C2), dictionary-
01(D1), dictionary-02(D2) – XML documents
generated by the XBench benchmark (Yao, 2002)
4. dblp(DB) – a collection of publications
As it can be seen in Table 1, the sizes of the
documents reach from a few hundred kilobytes to
more than 300 Megabytes.
Table 1: Sizes of documents of our datasets.
document XM H C1 C2 DB D1 D2
Uncompressed
size in MB
5.3 0.3 10.6 105.3 308.2 10.8 106.4
We have compared our approach with 3 other
approaches:
- XGrind (Tolani, 2002) – a queryable XML
compressor
- XMill (Liefke, 2000) – an XML compressor
- gzip
2
– a widely used text compressor
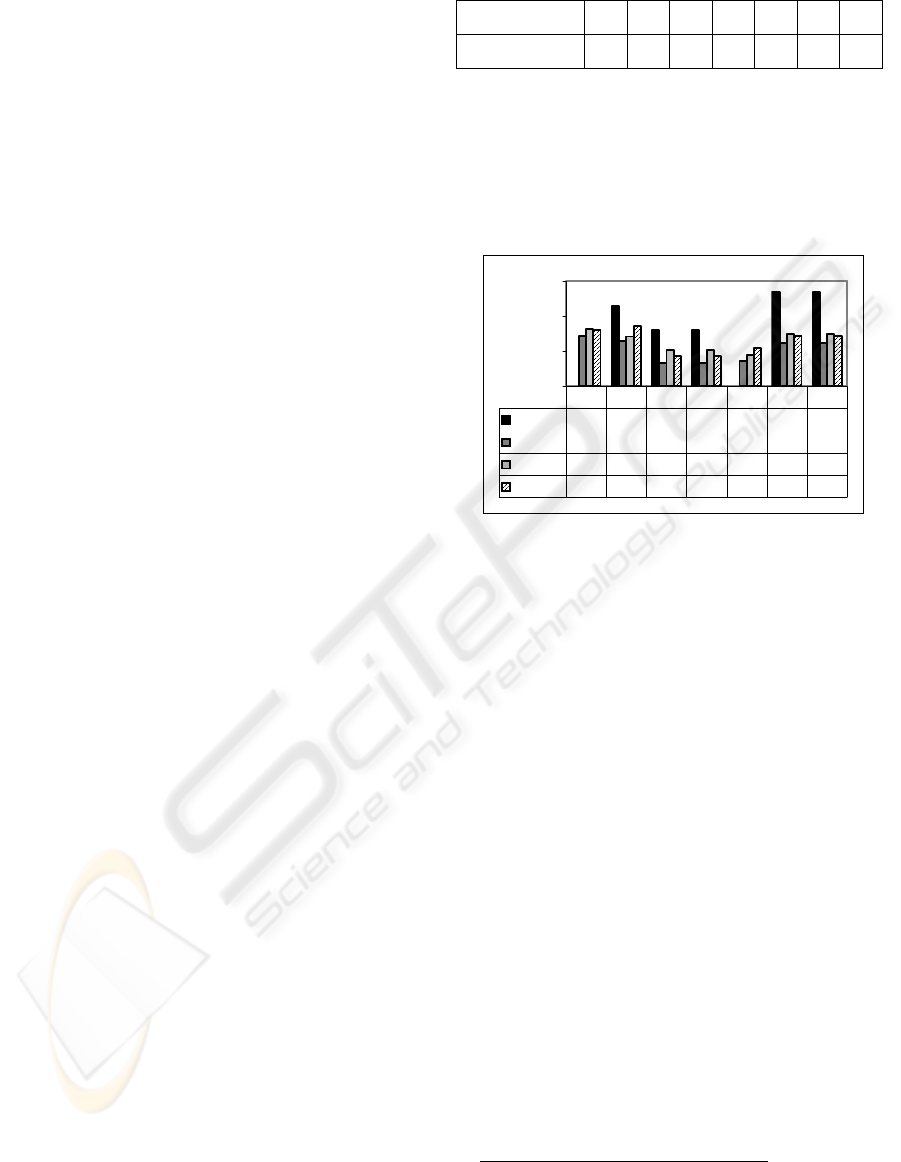
The results can be seen in Figure 2.
Figure 2: Compression ratio (size of the compressed data
divided by size of the original data).
Using these datasets, XMill performs better
achieving compression ratios that are 3-8% lower
than the compressions ratios reached by our
approach. However, in contrast to XMill, our
approach allows to evaluate queries on the
compressed data and to partially decompress data.
Compared to gzip, our approach achieves similar
compression ratios, although gzip – as well as XMill
– does not allow for evaluating queries on the
compressed data. The difference of the compression
ratios (gzip minus DTD subtraction) ranges from 6%
(the gzip compression ratio is 6% smaller) to -3%
(the gzip compression ratio is 3% bigger).
XGrind is the only compression approach in our
tests that is capable to evaluate queries on the
compressed data like our approach. Our results have
shown that our approach significantly outperforms
XGrind. In our dataset, our approach performs better
achieving compression ratios that are 12-25% lower
than the compression ratios achieved by XGrind
3
.
In a second series of measurements, we have
compared the size of the structural part of the
original XML document with the size of the KST.
This means that we have compared the structure to
2
http://www.gzip.org/
3
Note that on our test computer, we got access violations
when running XGrind on XM and DB and therefore the
compression ratios for these two documents are missing.
0%
20%
40%
60%
XGrind
46% 32% 32% 54% 54%
XMill
29% 26% 13% 13% 14% 25% 25%
gzip
33% 28% 21% 21% 18% 30% 30%
DTDSub
32% 34% 17% 17% 22% 29% 29%
XM H C1 C2 DB D1 D2
ICEIS 2007 - International Conference on Enterprise Information Systems
92
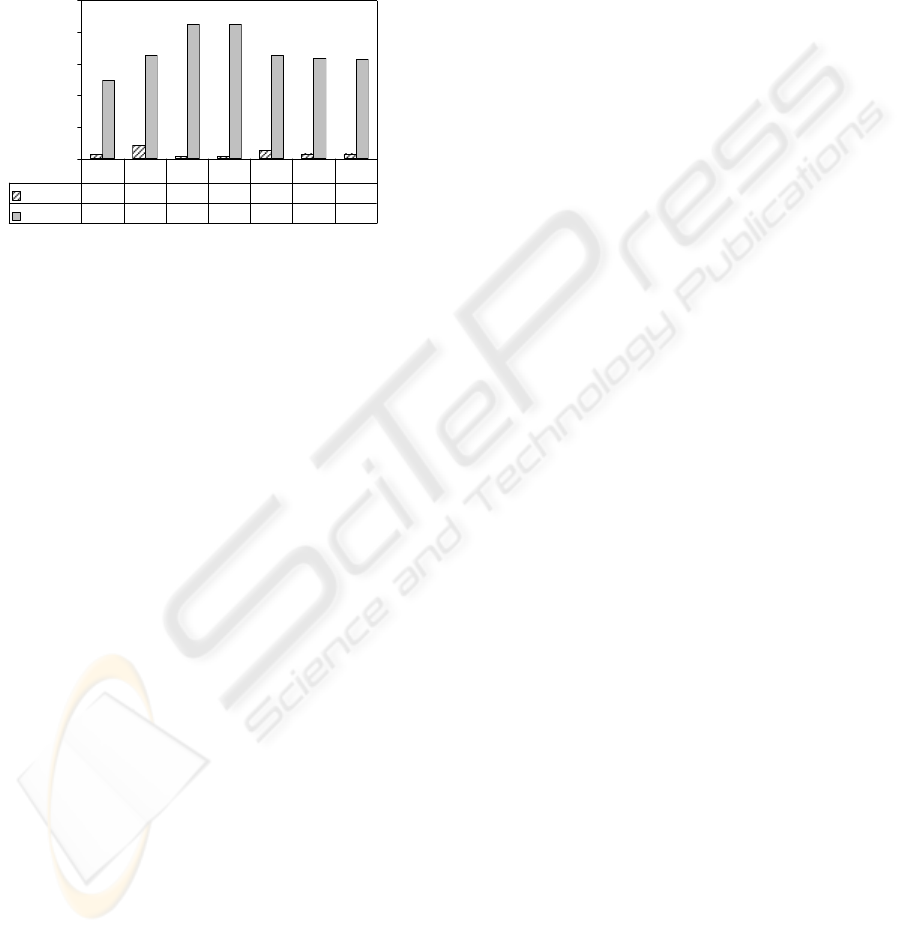
be parsed in order to evaluate XML path queries.
Our measurements have shown, that the size of the
KST ranges in average around 3.6% of the size of
the structural parts of the XML document. The
concrete results of our experiments can be seen in
Figure 3. |str|/|doc| means the size of the structural
part of the document divided by the document size
and |KST|/|str| means the size of the KST divided by
the size of the structural part of the document.
Figure 3: Relative size of the KST in comparison to the
uncompressed structure and relative size of uncompressed
structure in comparison to uncompressed document.
6 RELATION TO OTHER
WORKS
There exist several algorithms for XML
compression, which can be divided into categories
by their features: some compressed XML documents
can only be used to answer queries, if they are
decompressed, other algorithms allow querying the
compressed data. Another feature is whether XML
compression algorithms can be applied to data
streams or whether they can only be applied to static
XML documents.
The first approach to XML compression was the
XMill algorithm presented in (Liefke, 2000). It
compresses the structural information separately
from the data. The data is – according to the
enclosing tag – collected into several containers, and
the whole container is compressed afterwards. The
structure is compressed, by assigning each tag name
a unique and short ID. After the compression, the
compressed structure consists of the tag IDs which
represent a start tag, the container IDs which
represent a text value, and ‘/’-symbols which
represent an end tag. An appropriate compressing
algorithm is chosen for each container, depending on
the data type it contains. This approach does not
allow querying the compressed data and is not
applicable to data streams.
The approaches XGrind (Tolani, 2002), XPRESS
(Min, 2003) and XQueC (Arion, 2003) form
extensions of the XMill-approach. Each of these
approaches compresses the tag information using
dictionaries and Huffman-encoding (Huffmann,
1952) and replaces the end tags by either a ‘/’-
symbol or by parentheses. All three approaches
allow querying the compressed data, and, although
not explicitly mentioned, they all seem to be
applicable to data streams. A disadvantage of
XGrind is, that it does not support range queries
(e.g., //a[@b<50]), but only match queries (e.g.,
//a[@b=50]) or prefix queries. Instead, it allows a
validity test on compressed data using a DTD. In
contrast, XQuec supports range queries as well, as
XQuec uses an order-preserving compression
approach for the compression of the data.
XQzip (Cheng, 2004) and the approach presented
in (Buneman, 2003) compress the data structure of
an XML document bottom-up by combining
identical sub-trees. Afterwards, the data nodes are
attached to the leaf nodes, i.e., one leaf node may
point to several data nodes. The data is compressed
by an arbitrary compression approach. These
approaches allow querying compressed data, but
they are not applicable to data streams. In addition,
an approach to evaluate XQuery on the results of
(Buneman, 2003) is presented in (Buneman, 2005).
An extension of (Buneman, 2003) and (Cheng,
2004) is the BPLEX algorithm presented in
(Busatto, 2005). This approach does not only
combine identical sub-trees, but recognizes patterns
within the XML tree that may span several levels,
and therefore allows a higher degree of compression.
As its predecessors, it allows querying the
compressed data, but it is not applicable to data
streams.
In contrast to all these approaches, our algorithm
allows querying (including match, prefix and range
queries) and is applicable to data streams. It achieves
an even higher level of compression, as it only
contains compressed data plus some sparse
information added for each choice operator and each
kleene operator contained in the DTD. As our
compressed XML data contains nearly no structural
information, only valid documents can be
decompressed, i.e., our approach does not allow for
checking validity.
The approach presented in (Sundaresan, 2001)
follows the same basic ideas as our approach: omit
all information that is redundant because of the
DTD. But the idea to realise this idea is completely
different from our approach. In (Sundaresan, 2001) a
DOM-tree is built and traversed simultaneously for
the DTD and the XML document. Whenever the
document contains information not found in the
DTD, this information is written to the compressed
document. So the resulting compressed document is
0%
20%
40%
60%
80%
100%
|KST | / |str|
2,8% 8,3% 1,3% 1,3% 5,3% 3,1% 3,1%
|
str
|
/
|
doc
|
50% 66% 85% 85% 66% 63% 63%
XM H C1 C2 DB D1 D2
XML INDEX COMPRESSION BY DTD SUBTRACTION
93

nearly the same as in our case (e.g., text values are
encoded differently), but whereas our approach is
capable to sequentially compress infinite data
streams (and to perform path queries on the
compressed data) the approach presented in
(Sundaresan, 2001) is limited by the size of main
memory (According to (Sundaresan, 2001) they had
problems with a file of 281 kB (the smallest test file
in our data set), as it exceeded their time threshold,
whereas we were able to compress a document of
more than 300 MB in decent time).
Another approach (Ng, 2006) also follows the
idea to omit information that is redundant because of
the DTD. It is also using a SAX-parser, i.e., this
approach is capable to compress infinite data
streams. However, this approach uses the paths
allowed by a non-recursive DTD to define a set of
buffers and stores constants found in the XML
document in the buffer defined for their path before
compressing the whole buffer. As the number of
buffers must be finite, this approach does not
support recursive DTDs. Furthermore, (Ng, 2006)
leaves it open how to treat constants other than
numbers. In comparison, our approach can store text
constants and can handle recursive DTDs.
7 SUMMARY AND
CONCLUSIONS
Structure preserving compression of XML data
based on DTD subtraction reduces the verbose
structural parts of XML documents that are
redundant when regarding the structure of a given
DTD, but preserves enough information to search
for certain paths in the compressed XML data. Our
approach uses given DTD element declarations to
generate a set of grammar rules, which is then
augmented to an attribute grammar for either
compression of an XML document to a KST and a
CXML document, for decompression of a KST and
a CXML document or for translating XPath queries
into index positions on CXML data. Our approach
can be extended to arbitrary DTDs as well as to
other schema languages that allow to derive a set of
grammar rules (e.g., XML Schema and RelaxNG)
and to XML streams.
Of course, our structure preserving compression
technique can be combined with an ordinary
compression and decompression, i.e., a normal
compression and decompression technique could be
applied to the data generated by our structure
preserving compression, in order to send an even
less amount of data from a sender to a recipient.
Note however that our overall goal is not only to get
a low compression size, but the main focus of our
contribution is to enable path query processing on
compressed data.
As XPath forms the major part of other query
languages like XQuery and XSLT, we are optimistic
that our approach could also be applied to XQuery
and XSLT.
REFERENCES
Arion, A., Bonifati, A., Costa, G., D’Aguanno S.,
Manolescu, I., Pugliese, A., 2003. XQueC: Pushing
queries to compressed XML data. In Proc. VLDB.
Buneman, P., Choi, B., Fan, W., Hutchison, R., Mann, R.,
Viglas. S., 2005. Vectorizing and Querying Large
XML Repositories. In ICDE 2005.
Buneman P., Grohe, M., Koch, C., 2003. Path Queries on
Compressed XML. In VLDB 2003.
Busatto, G., Lohrey, M., Maneth, S., 2005. Efficient
Memory Representation of XML Documents. In
DBPL 2005.
Cheng, J., Ng, W., 2004. XQzip: Querying Compressed
XML Using Structural Indexing. In EDBT 2004.
Cloksin W.F., Mellish, C.S., 1997. Programming in
Prolog, Springer. Berlin, 4
th
Edition.
Fredkin, E., 1960. Trie Memory. In Communications of
the ACM.
Huffman, D., 1952. A Method for Construction of
Minimum-Redundancy Codes. In Proc. of IRE.
Liefke, H., Suciu, D., 2000. XMill: An Efficient
Compressor for XML Data. In Proc. of ACM
SIGMOD.
Min, J.K., Park, M.J., Chung, C.W., 2003. XPRESS: A
Queriable Compression for XML Data. In
Proceedings of SIGMOD.
Ng, W., Lam, W.-Y., Wood, P.T., Levene, M., 2006 XCQ:
A Queriable XML Compression System. In
Knowledge and Information Systems, Springer-Verlag.
Olteanu, D., Meuss, H., Furche, T., Bry, F., 2002. XPath:
Looking Forward. In EDBT Workshops 2002.
Schmidt, A., Waas, F., Kersten, M., Carey, M., Manolescu
I., Busse, R., 2002. XMark: A benchmark for XML
data management. In VLDB 2002.
Su, H., Rundensteiner, E.A., Mani, M., 2005. Semantic
Query Optimization for XQuery over XML Streams.
In VLDB 2005.
Sundaresan N., Moussa, R., 2001. Algorithms and
programming models for efficient representation of
XML for Internet applications. In WWW 2001.
Tolani, P.M., Hartisa, J.R., 2002. XGRIND: A query-
friendly XML compressor. In Proc. ICDE 2002.
Yao, B.B., Ozsu, M.T., Kennleyside, J., 2002. XBench - A
family of benchmarks for XML DBMSs. In
Proceedings of EEXTT.
Extensible Markup Language (XML) 1.0, 2000.
http://www.w3.org/TR/2000/REC-xml-20001006
Ziv, J., Lempel, A., 1977. A Universal Algorithm for
Sequential Data Compression. In IEEE Transactions
on Information Theory.
ICEIS 2007 - International Conference on Enterprise Information Systems
94
