
SUMMARIZING DOCUMENTS USING FRACTAL TECHNIQUES
M. Dolores Ruiz and Antonio B. Bail
´
on
Department of Computer Science and Artificial Intelligence, University of Granada
C/Daniel Saucedo Aranda s/n 18071, Granada, Spain
Keywords:
Fractal summarization, fractal dimension, summarization.
Abstract:
Every day we search new information in the web, and we found a lot of documents which contain pages with
a great amount of information. There is a big demand for automatic summarization in a rapid and precise
way. Many methods have been used in automatic extraction but most of them do not take into account the
hierarchical structure of the documents. A novel method using the structure of the document was introduced
by Yang and Wang in 2004. It is based in a fractal view method for controlling the information displayed. We
explain its drawbacks and we solve them using the new concept of fractal dimension of a text document to
achieve a better diversification of the extracted sentences improving the performance of the method.
1 INTRODUCTION
Nowadays, a lot of information is accesible in the
web, and many people can use this huge source to re-
trieve what they need. For example, users can check
e-mail, read news, buy products, etc. using a com-
puter, but at present the use of mobile and handheld
devices is growing significantly. However, the re-
duced dimensions of handheld devices limit the handy
visualization of large documents.
The visualization of summarized documents in a
portable device can facilitate a fast review of their
main content in just a few seconds. Organizations
need to make decisions as fast as possible, access to
large text documents or to other information sources
during decision making, and as a result, there is an
urgent need of a tool that summarizes the information
in a accurate and precise way.
Many methods have been used in automatic sum-
marization (Buyukkokten O., 2001).We can find in
the literature that those methods employ mainly three
techniques for the automatic single-document sum-
marization (Daume III H., 2005): sentence extrac-
tion, bag-of-words headline generation, and docu-
ment compression.
Research in sentence extraction started with the
works made by Luhn (Luhn, 1958) and Edmundson
(Edmundson, 1969). But recent techniques based in
the structure of the document had been proposed. A
novel model named fractal summarization has been
applied (Yang C. C., 2003b),(Yang C. C., 2003c)
based on the idea of fractal view of H. Koike (Koike,
1995) and on the techniques of fractal image com-
pression (Yang C. C., 2003a). The main idea is to
take into account the structure of the document and
the inheritance of the importance to the substructures,
but this method does not use all the information that
fractal structure gives.
The calculation of dimensions is a useful tool to
quantify structural information of artificial and natu-
ral objects. There are some types of dimension: the
Euclidean one, the Hausdorff-Besicovitch dimension,
and so on. We are going to work with the fractal di-
mension in the special case of text documents.
Fractal dimension of many objects cannot be de-
termined analytically but there are some good estima-
tors. We do a brief overview of some of them and
choose the most suitable for the calculation of fractal
dimension of text documents.
The paper follows with a description of the fea-
tures used in traditional summarization techniques.
We present their adaptations to structured documents.
Then we describe the fractal summarization method
26
Dolores Ruiz M. and B. Bailón A. (2007).
SUMMARIZING DOCUMENTS USING FRACTAL TECHNIQUES.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - SAIC, pages 26-33
DOI: 10.5220/0002363300260033
Copyright
c
SciTePress
given in (Yang C. C., 2003b) to comment its short-
comings, proposing some modifications to the propa-
gation formula. We follow with a review of how to
calculate the fractal dimension of text documents, fi-
nishing with the results of some experiments summa-
rizing web pages. We conclude with the conclusions
and the bibliography used.
2 STRUCTURE IN
SUMMARIZATION
TECHNIQUES
Many traditional summarization models involve the
extraction of sentences from the source document
based on some of its salient features. But the docu-
ment is considered as a sequence of sentences instead
of considering its hierarchical structure. The hierar-
chical structure of the document give to us more in-
formation about the importance of some paragraphs
depending on their location.
2.1 Hierarchical Structure of a Text
Document
In most of the cases we work with structured infor-
mation. When humans write a document they use an
important source of information: the structure. Using
a structured text we achieve a better division of infor-
mation and we give more importance to some parts
allocating them in special places. We are going to
use this property to transform the text document into
a tree.
Documents are usually hierarchical and can be
viewed as compositions of simpler constituents. A
document consists of chapters; a chapter consists of
sections; a section consists of subsections, a section
or subsection contains paragraphs; a paragraph con-
sists of sentences, and a sentence is a group of terms.
The smallest units which contain information are the
terms (words with significance for themselves; words
that are deemed irrelevant are eliminated). This is the
highest division we have considered. We will refer to
each level in the compositional structure of a docu-
ment depending of its position with regard to the title
of the document. Then, the original document is re-
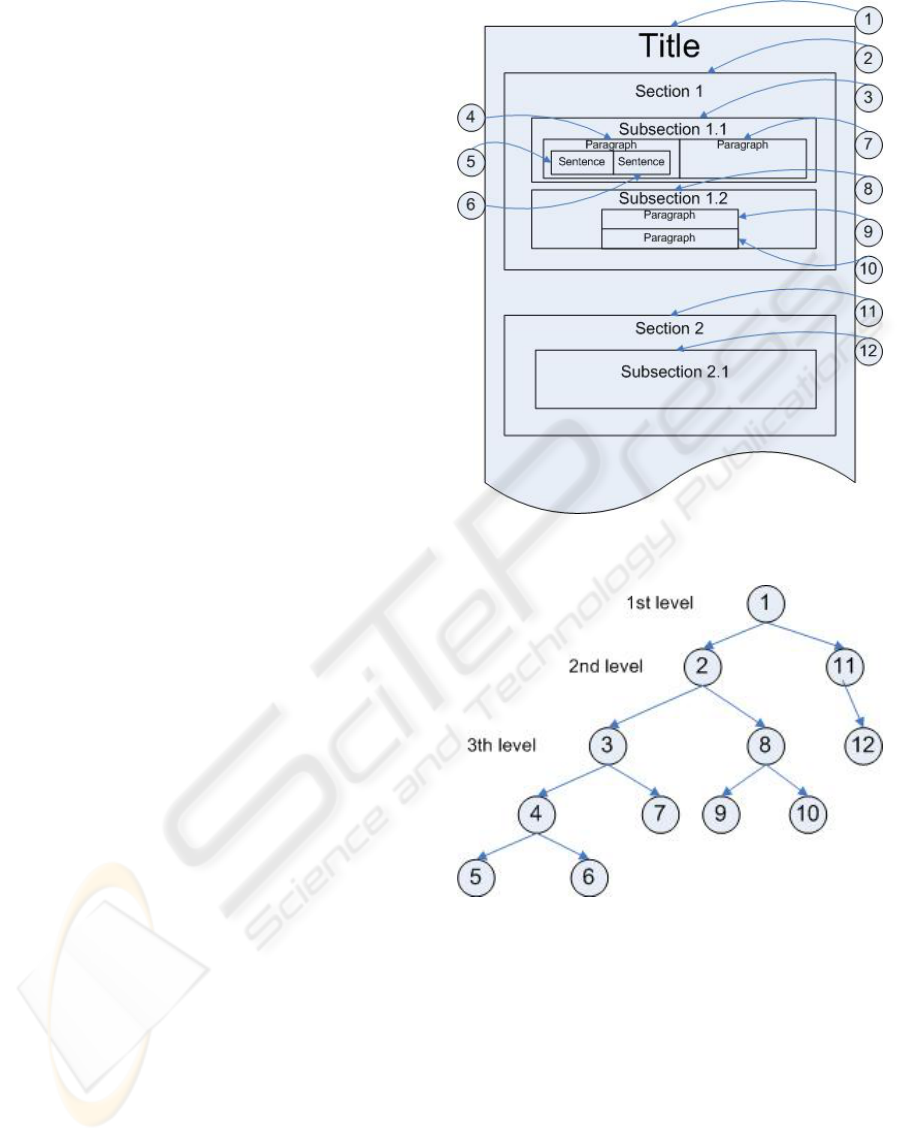
presented as a tree according to its structure. As
shown in figure 1, in the tree there is a inclusion rela-
tion between a node and its children. Every node in
the tree will contain all of its descendants. In this way,
the root or the tree represents the whole document, not
only the title; and the terms will be the leaves of the
tree.
Figure 1: Document hierarchical structure.
Figure 2: Tree associated to a text document.
2.2 Adaptation of Traditional Features
The most widely used summarization characteristics
are the thematic, location, heading and cue features.
These features have been modified according to the
structure of the document. We have used the adap-
tation of these features using the tree structure of the
document (Yang C. C., 2004).
• The thematic feature was first identified by Luhn
(Luhn, 1958) and then modified by Edmundson
(Edmundson, 1969). He proposed a thematic
SUMMARIZING DOCUMENTS USING FRACTAL TECHNIQUES
27

weight of keywords based on the term frequency.
The tfidf (Term Frequency, Inverse Document
Frecuency) score is the most used. We consider
the i
th
term in a document as t
i
. In our case, the
tfidf of the term t
i
in a node is defined as the term
frequency within the node inverse the numbers of
nodes at the same level that contains the term, i.e.,
w
ix
= t f
ix
× log
2
N
0
n
0
, (1)
where t f
ix
is the frequency of the term t
i
in the
node x, N
0
is the number of nodes in the docu-
ment at the same level as x and n
0
is the number
of nodes that contain the term t
i
in the document
at the same level. The Sentence Thematic Score,
SS
T
, of the k
th
sentence s
k
in the node x is calcu-
lated as the sum of the w
ix
of the constituent terms
t
i
of the sentence s
k
, i.e.,
SS
T
(s
k
,x) =
∑
t
i
∈s
k
w
ix
. (2)
The Thematic Score TS of the node x is again
calculated as the sum of the Sentence Thematic
Score of all the sentences in the node, i.e.,
T S(x) =
∑
s
k
∈x
SS
T
(s
k
,x). (3)
• Edmundson also considers the location feature
(Edmundson, 1969) as an indicator of the signifi-
cance of a sentence based on the hypotheses that
topic sentences tend to occur at the beginning or
the end of a document or paragraph. The Location
Score LS of a node x is calculated as the inverse
of the minimal distance of the node x to the first
node and the last node at the same level with the
same parent as x, i.e.,
LS(x) =
1
min{d(x, f nb(x)),d(x,lnb(x))}
(4)
where d(x,y) is the distance function that calcu-
lates the number of nodes at the same level under
the same parent between x and y, f nb(x) is the
first node brother of x, and lnb(x) is the last node
brother of x. See figure 3 as an example of this
feature.
• The third feature we have used is the heading fea-
ture. It is based on the hypotheses that the heading
contains the subject of the document summarized
in its words.
The Sentence Heading Score SS
H
of a sentence
s
k
has been modified to consider the structure of
the document. For example, at each level we have
to consider the previous headings giving a higher
weight when the heading is closer to the node we
are considering.
Figure 3: Location feature.
Let s
k
be the sentence into consideration that it
is included in the node x. Its Sentence Heading
Score would be the sum of the weights of the
terms t
i
that appears in it and in the heading of
other nodes z in the path from the root to the node
x.
This weight is computed as the sum of the weights
w
iz
seen in (1) of terms t
i
in the sentence s
k
divided
by the product of the numbers of children m
node
of
the nodes in the path from node z to node x, i.e.,
SS
H
(s
k
,x) =
∑
z∈ path from root to x
∑
t
i
∈z∩s
k
w
iz
∏
i∈ path form z to x
m
i
.
(5)
The Heading Score HS of node x is calculated as
the sum of the Sentence Heading Score of all sen-
tences in the node, i.e.,
HS(x) =
∑
s
k
∈x
SS
H
(s
k
,x). (6)
• The last feature we have considered is the cue fea-
ture. Humans pay more attention to the sections
which has bonus words such as conclusion. In the
tree we examine the headings predecessors to the
node and sum the cue weights of the terms t
i
being
in the cue dictionary and in the headings. The Cue
Score is
CS(x) =
∑
t
i
∈heading(x)
cue(t
i
) (7)
where cue(t
i
) is the cue weight of the term in the
dictionary.
All these features must be normalized because
they have different range of values. Therefore, we di-
vide each feature by its maximum score in the whole
document, so we have the normalized scores associ-
ated to the four features, NTS, NLS, NHS and NCS.
To calculate the total weight associated to a node we
only have to do a weighted sum of the normalized the-
matic, location, heading and cue score of the node.
ICEIS 2007 - International Conference on Enterprise Information Systems
28

We call this total punctuation the Node Significance
Score, NSS, i.e., NSS(x) is equal to
a
1
NT S(x)+a
2
NLS(x) + a
3
NHS(x)+a
4
NCS(x) (8)
where a
1
,a
2
,a
3
,a
4
are positive reals that sum 1. They
are chosen to adjust the weighting of the different
summarization features according to our preferences.
3 FRACTAL SUMMARIZATION
Many studies of human abstraction process has shown
that humans extract the sentences according to the
document structure. However, most traditional auto-
matic summarization techniques consider a document
only as a set of sentences ignoring the structure of
the document. Some advanced summarization models
take into account the structure to compute the proba-
bility of a sentence to be included in the summary.
Fractal summarization model was proposed by Yang
and Wang to generate a summary based on document
structure.
Fractal summarization is developed based on the
idea of fractal view (Koike, 1995) and adapting the
traditional models of automatic extraction. The im-
portant information is captured from the source text
by exploring the hierarchical structure and salient fea-
tures of the document. Therefore they adapted the
features considering the structure of the document.
3.1 Fractal View & First
Approximation to Fractal
Summarization
Fractal summarization was developed by Yang and
Wang (Yang C. C., 2004) based on the idea of frac-
tal view of Koike (Koike, 1995) and adapting the tra-
ditional models of automatic extraction. They use the
inheritance of values to transmit the importance of the
node inside the whole document and to give out the
number of sentences we have to extract from each of
its children according to their importance. But they
do it using fixed values for some parameters like the
fractal dimension. They also do a division into range
blocks (Yang C. C., 2003b),(Yang C. C., 2003a) of the
document.
Next subsections show the process to convert the
fractal view method for controlling information in a
fractal automatic summarization method.
3.1.1 Fractal View
Fractal view is a fractal-based method that provides a
mechanism to control the amount of information dis-
played (Koike, 1995). The idea is based on the pro-
perty of self-similarity of a fractal tree. A tree is made
of a lot of sub-trees; each of them is also a tree. They
represent the degree of importance of each node by
its fractal value and they propagate the importance to
other nodes with the following expression:
(
Fv
root
= 1
Fv
x
= Fv
p(x)
×C N
−1/D
p(x)
(9)
where Fv
x
is the fractal value of node x, p(x) de-
notes the parent node of x, N
p(x)
is the number of child
nodes of p(x), D is the fractal dimension, and C is a
constant value satisfying 0 < C ≤ 1. This constant is
used to distinguish when we have a single tree, in the
sense that each node has a unique branch, and in con-
clusion we have node-branch-node-branch-node etc.
In this special case we have to choose C 6= 1. In other
cases, the majority of them, we choose C = 1. Notice
that when D = 1 = C, the above formula at the first
level divide the fractal value of the root in N
root
equal
parts. Then, divide 1/N
root
in n
x
equal parts, where
n
x
is the number of children that node x has. So if
we sum the fractal values of all nodes with the same
parent, they sum the fractal value of the parent; and if
we sum Fv of all nodes at the same level, we have as a
result 1. That is, the formula share out in an equitable
form when D = 1.
3.1.2 First Approximation to Fractal
Summarization
In (Yang C. C., 2004) the authors adapt the techniques
of fractal view to propagate the values from parents
nodes to their child nodes using the fractal dimension
D = 1 in the equation 9. They first divide the docu-
ment into range blocks. Then they transform the do-
cument into a tree and for the propagation of values
they use the following formula:
Fv
root
= 1
Fv
x
= Fv
p(x)
×
NSS (x)
∑
y∈p(x)
NSS (y)
−1
(10)
where NSS(x) is the Significance Score associated to
the node x using a division into range blocks, p(x)
is the parent node of x, and the expression y ∈ p(x)
denotes that y is a child of p(x).
The above formula doesn’t take into account
the fractal dimension of the document proposed by
Koike. We are going to solve this problem computing
the fractal dimension of a text document.
SUMMARIZING DOCUMENTS USING FRACTAL TECHNIQUES
29
Other shortcoming is that they change in the frac-
tal view formula the number of child nodes N
p(x)
(an
integer number ≥ 1) for a rational number between 0
and 1. For this reason the formula does not work well.
We do some important changes in the formula
and introduce the calculation of the fractal dimension
associated to a text document. This diversifies the ex-
traction of sentences according to the content of the
different sections.
4 ENHANCED FRACTAL
SUMMARIZATION
To solve all problems, we propose some modifications
for the last formula. We adapt it for a well working
and we introduce the use of fractal dimension D as a
parameter and not as a fixed value.
So the hierarchical inheritance formula between
nodes we take into consideration is
Fv
root
= 1
Fv
x
= Fv
p(x)
×
NSS (x)
∑
y∈p(x)
NSS (y)
1/D(x)
(11)
where D(x) is the fractal dimension of the node x. The
value of D(x) can change depending of the amount of
information contained in the node x, and D(root) is
the fractal dimension of the document (see next sec-
tion 6). We have used the NSS(x) measure seen in
section 2 to measure the importance of the node using
the hierarchical structure of the document. For a more
complete comprehension of the formula we explain in
next sections the computation of the fractal dimension
of text documents.
The propagation formula (11) has the following
advantages:
• It takes into account the structure of the document,
because it is based on the fractal tree representa-
tion associated.
• Inheritance of values. When a parent node is very
important because it has a lot of information, we
want to extract many sentences from this node. To
do that the child node inherits the quota of sen-
tences (see 22) from its parent using the propaga-
tion formula (11).
5 FRACTAL DIMENSION
The calculation of dimensions is a useful tool to quan-
tify structural information of artificial and natural ob-
jects. There are some types of dimension: the Eu-
clidean one, the Hausdorff-Besicovitch dimension,
and so on (Kraft, 1995).
The dimension that everybody knows is the Eu-
clidean one. A point has dimension 0, a line has
dimension 1, a plane has dimension 2 and when we
work in the space we say that it has dimension 3. For
example we are three-dimensional entities. But not all
the objects in this world have integer dimensions. The
matematicians since the nineteenth century have met
with other objects like the Cantor Set and the Koch
Curve whose dimensions are real numbers instead of
integers.
Mandelbrot told that a fractal is a shape made of
parts similar to the whole (Mandelbrot, 1986). This
definition uses the concept of self-similarity. We say
a set is strictly self-similar if we broke it into arbitrary
small pieces and each of them is a replica of the entire
set. When this happens the calculation of the fractal
dimension is easier.
Imagine we have a segment of length 1. We can
put two segments of length 6/10 each one at the end of
the branch. We can repeat this process till the infinity
(see figure 4). In this case the fractal dimension is
very easy to calculate because of the self-similarity
property of the tree that we have built, and is
D = − log
6
10
2 ≈ 1.36. (12)
. . .
Figure 4: Fractal tree.
If we generalize this construction when the tree
has N children at each node (cross of two or more
branches) and any branch is r times longer than that
of the previous branch, the dimension of the tree can
be calculated as
D = − log
r
N. (13)
This type of special tree is called a fractal tree and
we have seen that its fractal dimension is uniquely de-
fined by the above formula.
But exact fractal dimension can only be calculated
for ideal mathematical objects. For the rest we need to
use methods to approximate the fractal dimension. In
the literature there are different methods to calculate
the fractal dimension.
ICEIS 2007 - International Conference on Enterprise Information Systems
30

One of them is the Box-counting method. It basis
on the idea of covering the object with a grid of boxes
of smaller size in each iteration, and then compute
the frequency which data points fall into each box.
But the box-counting can be computed only for low-
dimensional sets because the algorithmic complexity
grows exponentially with the set dimension. Besides
this, it is too difficult to select the best suited grid to
the object. Notice that this method uses the coordi-
nates of the points to allocate them into their corre-
sponding box. See (Liebovitch, 1989) for more de-
tails.
If we estimate the dimension of a curve (e.g. cell
membrane, coastline, landscape edge) we can use the
Compass method (Kraft, 1995). The procedure is
analogous to moving a compass with a fixed length δ
along the curve. The estimated length of the curve is
the product of the number of rulers required to ‘cover’
the object and the scale factor δ. The relationship
between the length L, δ, and the fractal dimension D
is L = kδ
1−D
where k is a constant. The fractal di-
mension is estimated by measuring the length of the
curve at various scale values δ. This method is only
for curves and it is exact for self-similar curves.
Another method used to calculate the correlation
dimension (Grasberger P., 1983) is a good substitute
of the box-counting method due to its computational
simplicity. In each iteration we choose circles of
a fixed ratio in decreasing order and then count the
number of data points that fall in each circle.
There are other methods in the literature but many
of them are used with special types of objects using
in each case their particular characteristics (spatial or
temporal series, point patterns information theory and
diversity, topographic surfaces, etc.). For a more com-
plete view of this topic consult (Camastra F., 2002),
(Kraft, 1995) and (Grasberger P., 1983).
The disadvantages of the box-counting method
and the inappropriate use of coordinates in a text do-
cument to designate the sentences or words in it, are
some of the reasons to reject the method. The com-
pass method is used only for curves and it is inappro-
priate when curves have intersections. However the
correlation dimension uses a distance function that we
are going to adapt to our document using its structure.
This is the reason to choose the Grasberger and Pro-
caccia method to calculate the fractal dimension of a
text document.
6 FRACTAL DIMENSION OF A
TEXT DOCUMENT
We are going to work with the fractal dimension in
the special case of text documents. Fractal dimension
of many objects cannot be determined analytically, in
those cases we can use some estimators of the fractal
dimension. For text documents we are going to use
the Grasberger and Procaccia method (Grasberger P.,
1983).
To calculate the fractal dimension we need the tree
associated to the document, and we have to define a
distance function between any two nodes. Let N be
the number of nodes in the tree, R the maximum num-
ber of levels of the document (it will be the maximum
number of branches between the root node and the last
node in all directions), and I the indicator function de-
fined as 1 if it is true and 0 in the rest of cases. To de-
fine the distance between two arbitrary nodes we first
need a function that tell us how similar are two nodes.
For this purpose we take the cosine measure (Daume
III H., 2005),
cos(x,y) =
∑
t
i
∈x
w
ix
∑
t
i
∈y
w
iy
r
∑
t
i
∈x
w
2
ix
r
∑
t
i
∈y
w
2
iy
(14)
where we have used the t f id f weighting in equation
(1) associated to the node. Another similarity mea-
sures can be founded in (Guerrini G., 2006).
With this definition, the cosine takes values
between 0 and 1, having a value very near to 1 when
nodes have similar contents. For that reason we take
the distance between nodes x and y as
dist(x,y) = 1 − cos(x, y). (15)
Let x
i
, x
j
two arbitrary nodes, there is always a
path joining them. Suppose x
i
= x
1
,x
2
,...,x
n
= x
j
is
the shortest path between the two nodes. Then the
distance between x
i
and x
j
is
x
j
− x
i
=
n−1
∑
l=1
dist(x
l
,x
l+1
)
2R
. (16)
Next, we calculate the correlation integral C
m
(r
k
)
(see the Grasberguer and Procaccia method in (Gras-
berger P., 1983) and (Ruiz M. D., 2006)) for each
r
k
= (2R − k)/(2R) (17)
with k = 1,...,2R − 1, that is, we do
C
m
(r
k
) =
2
N(N − 1)
N
∑
i=1
N
∑
j=i+1
I(
x
j
− x
i
≤ r
k
) (18)
SUMMARIZING DOCUMENTS USING FRACTAL TECHNIQUES
31
where N is the number of nodes in the tree and R is
the maximum number of levels of the document, and
I is the indicator function:
I(λ) =
(
1 if λ is true
0 rest of cases.
(19)
The correlation dimension is then defined with the
formula
D = lim
r
k
→0
ln(C
m
(r
k
))
ln(r
k
)
. (20)
But in practice we can calculate it computing
the slope of the regression line that the points
(ln(r
k
),ln(C
m
(r
k
))) form.
This approximation to the calculation of the frac-
tal dimension of a text document indicates the distri-
bution of the information in the document. The above
distance function tells how similar are the contents of
the node x
j
and the node x
i
. If they are very far, the
distance will be small and therefore it won’t count in
the sum.
Some experiments with web pages for computing
the fractal dimension of texts can be found in (Ruiz
M. D., 2006).
7 FRACTAL SUMMARIZATION
ALGORITHM
Now we propose the algorithm for the process of au-
tomatic summarization using the propagation formula
in (11) and then we explain how it works with more
details.
We define the compression ratio, r, of summariza-
tion as the number of sentences we would like to be
in the summary divided by the number of sentences
of the document, i.e.,
r =
# sentences of summary
# sentences of document
. (21)
This is the ideal definition, but the number of sen-
tences we are going to extract depends on the size of
the document. It has been proved that extraction of
20% sentences can be as informative as the full text
of the source document (Morris G., 1992). But the
users can also choose the number of sentences they
want to extract and change it if they are interested or
not in the content of the document.
The quota of the summary is the compression ra-
tio times the number of sentences of the document,
and we propagate the quota to the child nodes by the
formula
quota
x
= Fv
p(x)
× quota
p(x)
(22)
Algorithm 1 : Fractal Summarization.
1. Choose a compression ratio.
2. Choose a threshold value.
3. Calculate the sentence number quota of the sum-
mary.
4. Transform the document into a fractal tree.
5. Calculate the fractal dimension of each node of the
document.
6. Set the current node to the root of the fractal tree.
7. Repeat
7.1 For each child node under current node, cal-
culate the fractal value of child node.
7.2 Allocate quota to child nodes in proportion
to fractal values.
7.3 For each child nodes.
If the quota is less than threshold value
Select the sentences in the node by ex-
traction.
Else
Set the current node to the child node
Repeat steps 7.1, 7.2, 7.3.
8. Until all the child nodes under current node are
processed.
where x is the child node and p(x) denotes de parent
node of x.
The threshold value is the maximum number of
sentences that we want to extract from the same node.
The optimum value is between 3 and 5 (Goldstein J.,
1999). This threshold value is going to prevent the
appearance of overlapped sentences in the summary
because we will extract few sentences of each para-
graph.
8 EXPERIMENTS AND RESULTS
We have used this automatic summarization method
in web pages with a large content of text and with a
good structure in the sense that for the title they use
the markup tags < H1 >, for the sections < H2 >,
< H3 > for the subsections, etc. with their corre-
sponding close markup tags < /H1 >, < /H2 >, etc.
We do a fractal tree using the above structure and
when we are at the last level we choose only the terms
with significance, that is we drop all the articles, ordi-
nal and cardinal numbers, the verb to be, prepositions,
pronouns, conjunctions, etc. We can see an example
of tree associated to a document in the figure 2. For
the cue feature we take the page keywords to form the
dictionary of bonus words. And we have considered
the coefficients in (8) all of them equal to 1/4, that is,
we give the same importance to the four salient fea-
ICEIS 2007 - International Conference on Enterprise Information Systems
32

tures of the document.
We have run some experiments with a wide range
type of web pages and we observe the following facts:
• The method achieve a good performance with
documents that have several levels of granularity,
in other words, when the tree associated to the
document has many levels and the nodes have a
lot of branches, the calculation of the fractal di-
mension helps to get a summary with information
more diversified according to the document struc-
ture.
• With wrong structured web pages the method ob-
tains bad results since the calculation of fractal di-
mension doesn’t give information in those cases.
In conclusion, we have seen in our experiments
that traditional summarization extracts most of the
sentences from few chapters, fractal summarization
with D = 1 extracts the sentences distributively from
each section, and with our new approximation using
the fractal dimension of the document, the method
share out the sentences according to their content and
their position.
9 CONCLUSIONS
In this paper, we present an improvement to the frac-
tal summarization method. The propagation formula
have been modified according to the fractal view
method, and it uses the novel concept of fractal di-
mension of text documents presented in (Ruiz M. D.,
2006).
We have used this automatic summarization
method in web pages with a large content of text and
with a good structure as in figure 2, giving very good
results and showing the good performance of the pro-
posed method.
In the future, we are going to use a similarity mea-
sure taking into account the semantic of words giving
a more complete solution to the problem of summa-
rizing documents. Moreover, we are working about
the problem of summarizing the document according
the preferences of the user, giving more importance
to those sections that the user wants to spread out
using the fractal dimension. We also want to adapt our
method in the case of summarizing a group of docu-
ments with similar contents.
REFERENCES
Buyukkokten O., Garcia-Molina H., P. A. (2001). See-
ing the whole in parts: Text summarization for web
browsing on handheld devices. In 10
th
International
WWW Conference, Hong Kong.
Camastra F., V. A. (2002). Estimating the intrinsic dimen-
sion of data with a fractal-based method. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence.
Daume III H., M. D. (2005). Induction of word and phrase
alignments for automatic document summarization.
Computational Linguistics, 31 (4):505–530.
Edmundson, H. P. (1969). New methods in automatic ex-
tracting. Journal of the Association for Computing
Machinery, 16 (2):264–285.
Goldstein J., Kantrowitx M., M. V. C. J. (1999). Summariz-
ing text documents: sentence selection and evaluation
metrics. pages 121–128.
Grasberger P., P. I. (1983). Measuring the strangeness of
strange attractors. pages 189–208.
Guerrini G., Mesiti M., S. I. (2006). An overview of similar-
ity measures for clustering XML documents. Chapter
in Athena Vakali and George Pallis (eds.).
Koike, H. (1995). Fractal views: a fractal-based method for
controlling information display. ACM Transactions on
Information Systems, 13 (3):305–323.
Kraft, R. (1995). Fractals and dimensions. HTTP-Protocol
at www.weihenstephan.de.
Liebovitch, L. S., T. T. (1989). A fast algorithm to deter-
mine fractal dimensions by box counting. Physics Let-
ters A, 141 (8,9):386–390.
Luhn, H. P. (195 8). The automatic creation of literature
abstracts. IBM Journal, pages 159–165.
Mandelbrot, B. B. (1986). Self-affine fractal sets. Pietronero
L. & Tosatti E. (eds.): Fractals in Physics, Amster-
dam.
Morris G., Kasper G. M., A. D. A. (1992). The effect and
limitation of automated text condensing on reading
comprehension performance. Information System Re-
search, pages 17–35.
Ruiz M. D., B. A. B. (2006). Fractal dimension of text
documents: Application in fractal summarization. In
IADIS International Conference WWW/Internet, vol-
ume 2, pages 349–353.
Yang C. C., Chen H., H. K. (2003a). Visualization of large
category map for internet browsing. Decision Support
Systems, 35:89–102.
Yang C. C., W. F. L. (2003b). Fractal summarization for mo-
bile devices to access large documents on the web. In
12
th
International WWW Conference, Budapest, Hun-
gary.
Yang C. C., W. F. L. (2003c). Fractal summarization: Sum-
marization based on fractal theory. In SIGIR 2003,
Toronto, Canada.
Yang C. C., W. F. L. (2004). A relevance feedback model
for fractal summarization. Lecture Notes in Computer
Science, 3334:368–377.
SUMMARIZING DOCUMENTS USING FRACTAL TECHNIQUES
33
