
MAKING INCOMPLETE INFORMATION
VISIBLE IN WORKFLOW SYSTEMS
Georg Peters
Munich University of Applied Sciences
Faculty of Computer Science and Mathematics
Lothstrasse 34, 80637 Munich, Germany
Roger Tagg
University of South Australia, School of Computer and Information Science
Mawson Lakes, SA 5095 Australia
Keywords: Workflow Systems, Process Mining, Partial Information, Soft Computing, Rough Sets.
Abstract: After a bumpy start in the nineties of the last century workflow systems have recently re-gained the focus of
attention. Today they are considered as a crucial part of the recently introduced middleware based ERP
systems. One of the central objectives and hopes for this technology is to make companies more process-
orientated and flexible to keep up with the increasing speed of change of a global economy. This requires
sophisticated instruments to optimally manage workflow systems, e.g. to deal with incomplete information
effectively. In this paper we investigate the potential of rough set theory to make missing or incomplete
information visible in workflow systems.
1 INTRODUCTION
After a breezy start in the nineties of the last century
and a decline soon afterwards, workflow systems are
now considered among the key enablers for
middleware based ERP-systems.
Van der Aalst and van Hee (2002) describe four
phases of information systems: which started with
the initial phase, that of decomposed applications.
Then successively the data and the user interface
management were taken out of the application.
Today, the (business) processes are being taken out
of the applications and are managed in specially
design process management software. Workflow
systems form a key technology in achieving this last
phase.
The main intention with this new approach is to
make a company more flexible and provide it with
better possibilities to adapt to new market
challenges. This has become of increasing
importance since the trend towards a global
economy requires companies to adapt to market
changes quicker than some 20 or 30 years ago.
However, the environment of companies today,
as well as being subject to high degrees of change, is
characterized by insecurity and vagueness. To deal
with vagueness, soft computing (Hoffmann et al.
2005) or granular computing (Bargiela, Pedrycz
2002) concepts provide well accepted methods.
Under these umbrellas fuzzy sets, neutral nets,
genetic algorithms and other techniques are
subsumed to provide a rich toolbox to deal formally
with the vagueness which is immanent in the real
world.
Recently rough set theory (Pawlak 1982) has
gained increasing attention and has established itself
as a concept of soft computing. It is an approach to
better deal with certainty, indiscernibility and similar
situations.
In the meantime rough sets have been rapidly
extended theoretically and many areas of
applications have been suggested. These cover
bioinformatics (e.g. Mitra 2004), pattern recognition
(e.g. Skowron et al. 2001), multi-criteria decision
support (e.g. Slowinski 1993), case-based reasoning
(e.g. Polkowski et al. 1996), concurrent processes
(e.g. Suraj 2000) and many more.
434
Peters G. and Tagg R. (2007).
MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - ISAS, pages 434-440
DOI: 10.5220/0002361804340440
Copyright
c
SciTePress
The objective of this paper is to utilize the
concept of rough sets to make partial or incomplete
information in workflow systems visible, in order to
deal with it more effectively.
The remainder of the paper is organized as
follows. In the next Section we give a short
introduction to rough set theory. In Section 3 we
apply the concept of rough sets to workflow
systems. Section 4 discusses how these ideas might
be offered to process managers and end users. The
paper ends with a short conclusion.
2 ROUGH SETS
2.1 Fundamentals of Rough Set Theory
Since Pawlak introduced rough sets in 1982 (Pawlak
1982, 1992) they have gained increasing importance
and are today considered as a central part of soft
computing and granular computing.
The basic idea of rough set theory is that there
are two kinds of objects. While some objects are
clearly distinguishable from each other some objects
are indiscernible - normally because of missing or
incomplete information.
This has led to the concept of lower and upper
approximations of sets. An object in a lower
approximation of a set surely belongs to the set,
while an object in an upper approximation only may
belong to the corresponding set. Consequently it
cannot be a member of more than one lower
approximation simultaneously. The area of an upper
approximation that is not covered by a lower
approximation is often called a boundary area.
Lower Approximation of a Set
Upper Approximation of a Set
Lower Approximation of a Set
Upper Approximation of a Set
Boundary AreaBoundary Area
Figure 1: Lower and Upper Approximations.
This leads to the three basic properties of rough
set theory:
1. An object can be a member of one lower
approximation at most.
2. An object that is a member of the lower
approximation of a set is also member of the
upper approximation of the same set.
3. An object that does not belong to any lower
approximation is member of at least two
upper approximations.
In the context of this paper we limit our
presentation of the fundamentals of rough sets to
these three properties. However, rough set theory is
much richer and covers such aspects as certainty
versus coverage, global and local coverage, reducts,
indiscernability relations, minimal complex and
many more. For a basic introduction to rough sets
theory see (Grzymala-Busse, 2004). More detailed
surveys, specially on its mathematical foundations,
can be found for example in (Komorowski. 1999) or
(Polkowski, 2003).
Note that in contrast to fuzzy set theory (Zadeh,
1965; Zimmermann, 2001) where an object belongs
to more than one set simultaneously (indicated by
membership degrees), in rough set theory it is
assumed that an object belongs to one and only one
set. However, due to missing or contradictory
information the actual memberships of the objects in
the boundary areas remain unclear. See e.g. Dubois
and Prade (1990) for a detailed discussion on the
relationship of fuzzy and rough sets.
2.2 An Example for Rough Sets
Consider the following example (Grzymala-Busse
2004) dealing with a decision table of eight patients
showing different symptoms (Table 1). Four of the
patients are well while the remaining four patients
suffer from flu: decision {Flu=yes}.
Table 1: Patient’s Decision Tree.
# Temp-
erature
Headache Nausea Decision:
Flu
1. high yes no yes
2. very_high yes yes yes
3. high no no no
4. high yes yes yes
5. high yes yes no
6. normal yes no no
7. normal no yes no
8. normal yes no yes
Patients #1 and #2 belong to the lower
approximation of the set {Flu=yes} since there are
no conflicts with the diagnoses of the remaining
patients. The same applies to patients #3 and #7.
MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS
435
They belong to the lower approximation of the set
{flu=no}.
This means that patients showing the same
symptoms as patients #1 and #2 can be considered as
ill and patients with the same symptoms of patients
#3 and #7 are without flu.
However with the data shown, a diagnosis is not
possible for patients showing the same symptoms as
patients #4, #5, #6 and #8. There are contradictions
or missing information in this data set.
Patients #4 and #5 have the same symptoms
{high, yes, yes}, however patient #4 suffers from flu
while #5 is well. The same applies to patients #6 and
#8 with the symptoms {normal, yes, no} but
different diagnoses.
2.3 Interval Based Rough Sets
While original rough set theory is purely set-based, a
new interval driven approach has been established in
the meantime (e.g. Yao et al. 1994). Applications of
interval based rough set theory are in the field of
cluster analysis (Lingras et al. 2004, Peters 2006)
and others.
3 ROUGH WORKFLOW
MANAGEMENT
3.1 Rough Petri Nets
Rough Petri nets were introduced by J.K. Peters et
al. (1998, 1999, 2000, 2003).
The central idea of rough Petri nets is to design a
rough guard (soft guard) which determines whether
a transition is enabled or not. Peters et al. discuss the
properties of their rough Petri nets by giving
examples of sensor and filter models.
3.2 Utilizing Rough Sets in Workflow
Management
Many notations for the design of workflows have
been suggested, e.g. eEPC (Scheer 2000), UML
(Fowler 2003) or Petri nets (Murata 1989). The
relationships of these approaches have been
discussed extensively and transformation rules
between them have been suggested (e.g. van der
Aalst 1999; van Hee, 2005).
So, following Peters et al., we will make use of
the Petri net notation to show the potential of rough
set theory for workflow management. The main
reason for choosing this notation lies in the strong
mathematical foundations of Petri nets that make it
easier to integrate rough sets.
However, in contrast to Peters et al., we will
restrict our presentation to the basic idea of rough
sets. We furthermore focus on the “story” and avoid
formal representations as far as possible. Our focus
lies on the detection of incomplete and missing
information in workflow systems rather than in the
design of soft guards.
3.2.1 Patient’s Decision Tree as a Petri Net
Consider again the example given in Section 2.2.
The decision tree can be designed as a simple Petri
net consisting mainly of an (exclusive) OR-construct
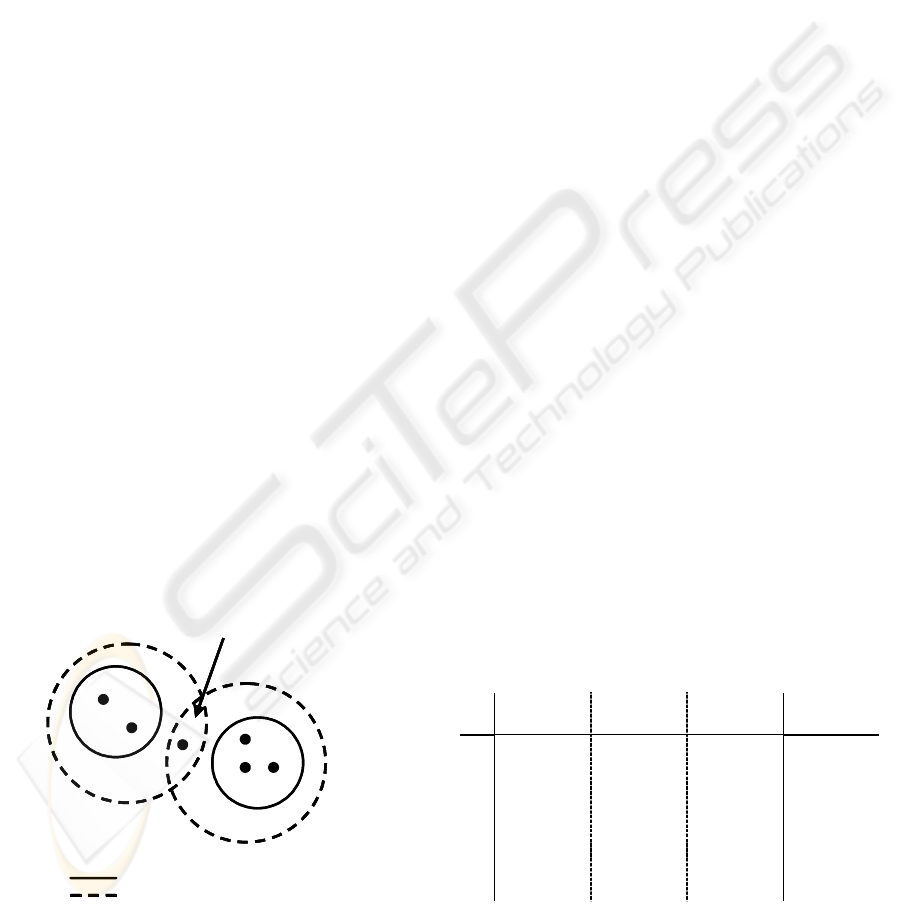
and the patients symbolised as tokens (see Figure 2).
For simplicity we will only display patients #1 and
#2 in
Figure 2.
…
…
Flu=yes
Flu=no
Patient #1
{high, yes, no}
Patient #2
{very_high, yes, yes}
A
B
Figure 2: Patient’s Decision Tree as a Petri Net.
Both of the explicitly displayed patients (#1 and
#2) fulfil the condition {flu=yes} and therefore
continue in branch A of the Petri net for possible
treatments of their illnesses. The same applies to
patients having the same symptoms as #3 and #4.
They continue in branch B of the Petri net where
they possibly return home since they are not ill.
However, the remaining patients with symptoms
equal to #4 and #5 as well as #6 and #8 get stuck
here. On the basis of their symptoms, no decision
can be made as to whether they have flu or not. In
other words, the training set did not provide enough
information to deal with patients having the
symptoms {high, yes, yes} and {normal, yes, no}.
3.2.2 Rough Tokens
Now we can apply rough set terminology to the
situation as described above.
We will distinguish between two views of the
tokens:
ICEIS 2007 - International Conference on Enterprise Information Systems
436
The local view on a token only considers the
pending decision that means only the next OR-
split.
Taking the global view we look at the whole
Petri net which means all OR-splits of the net
are considered.
This leads to the following definitions of locally
and globally rough tokens.
3.2.2.1 Locally Rough Tokens
Let us assume that the net as shown in Figure 2 is a
part of a much larger Petri net. So we have a local
view on the two tokens waiting to be routed to
branch A or B of the net.
Since both tokens have attributes that assign
them unambiguously to the set {flu=yes} they
belong to the lower approximation of this set. To
indicate that we only consider the next pending
decision we say that the tokens belong to a local
lower approximation of the Petri net specified by the
place they are occupying and the corresponding
decision {flu=yes}.
Again the same applies to tokens with the
attributes {high, no, no} (according to sample
patient #3) and {normal, no, no} (according to
sample patient #7). Following our arguments given
above they can be assigned to the local lower
approximation of the set {flu=no}.
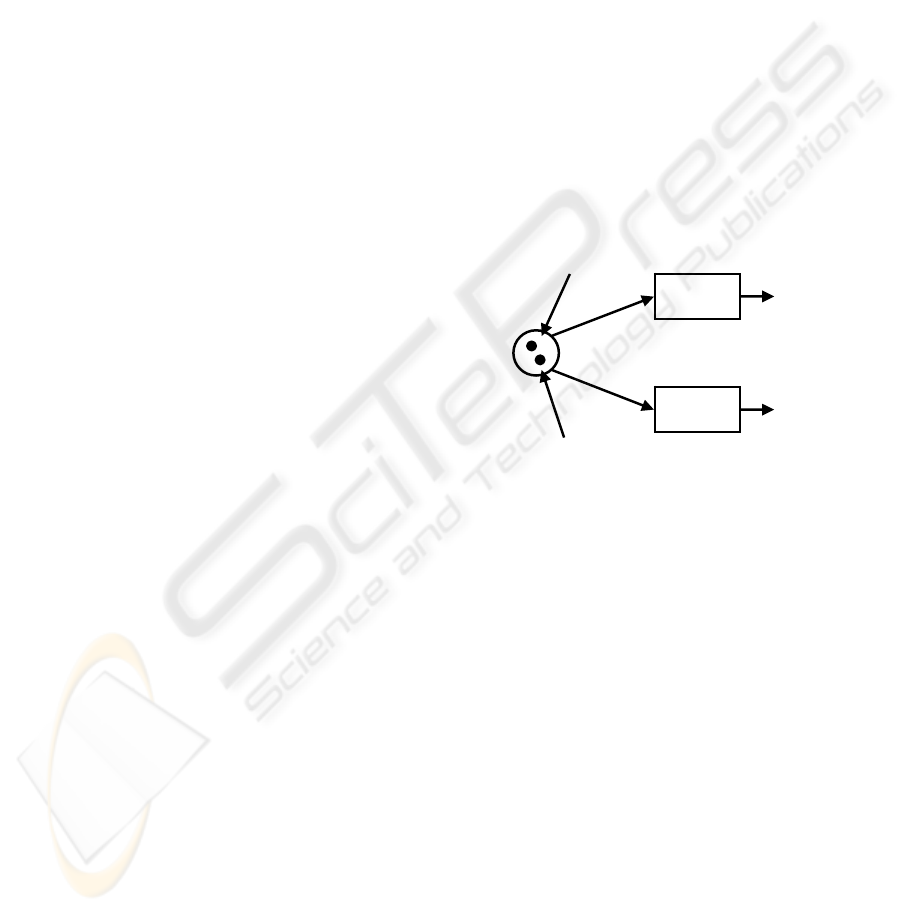
…
…
Flu=yes
Flu=no
Token in a local
upper approximation,
e.g. {normal, yes, no}
A
B
Token in a local
lower approximation,
e.g. {high, yes, no}
Figure 3: Patient’s Decision Tree as a Petri Net.
Unfortunately patients with the attributes {high,
yes, yes} and {normal, yes, no} cannot be directed
to either branch A or B of the net. They could be ill
or they could be healthy. To indicate this vagueness,
these patients are assigned to the local
approximation of the set {flu=yes} and
simultaneously to the local approximation of the set
{flu=no}. Similarly on the lower approximations we
put the attribute “local” in front of the term “upper
approximation” to indicate the local perspective
limited to one OR-split.
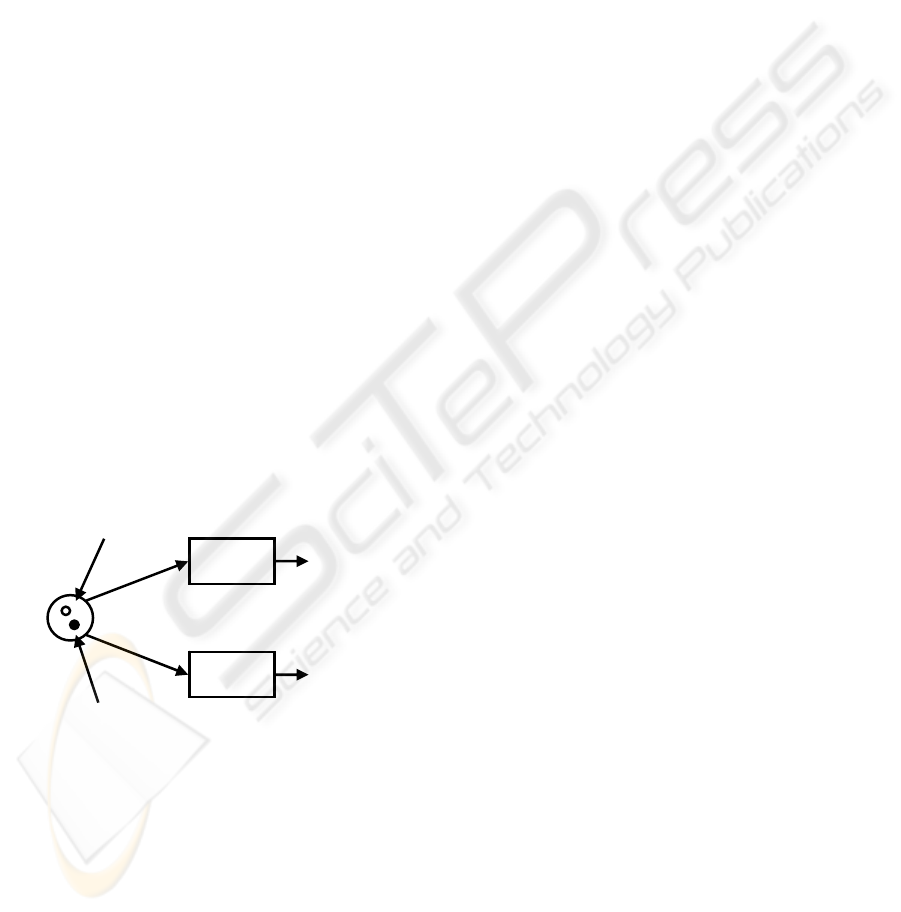
Finally, to graphically distinguish between tokens
(patients) belonging to one local lower or two or
more local upper approximations we suggest their
representation as show in
Figure 3.
The token with the white area in its middle is
stuck at the place, while the completely black token
will be consumed by the transition on branch A.
3.2.2.2 Globally Rough Tokens
Besides the local view that is restricted to one OR-
split, it is also very desirable that a token carries
enough information with it to make it from the start
to the end of a Petri net without the need for
additional information.
Please note, for the sake of simplicity our
formulation is somewhat superficial here. To be
exact a transition consumes tokens from its input
places and produces totally new tokens for its output
places. However this generalization of our concept is
straight forwardly.
Obviously we have the following relationships
between the global and the local views:
Only tokens that never belong to any local
upper approximation carry sufficient
information to finish the Petri net without the
need for additional external information. To
indicate this we say that they belong to the
global lower approximation of the Petri net (in
contrast to the local lower approximation.
Any other tokens, i.e. that belong to a local
upper approximation at least one time,
consequently belong to the global upper
approximation (= upper approximation of the
Petri net). These tokens do not have sufficient
internal information to complete the net and
depend on, e.g., external guidance.
So the global view can directly be derived out of
the local view and is an aggregated perspective on
the Petri net.
3.2.3 Rough Places
In the previous section our focus was on the tokens.
In contrast to this we now investigate the role of the
places in respect to the viewpoint of rough
information.
Assume a given number of tokens arrive at an
OR-split. If the decision rule of the OR-split has
MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS
437
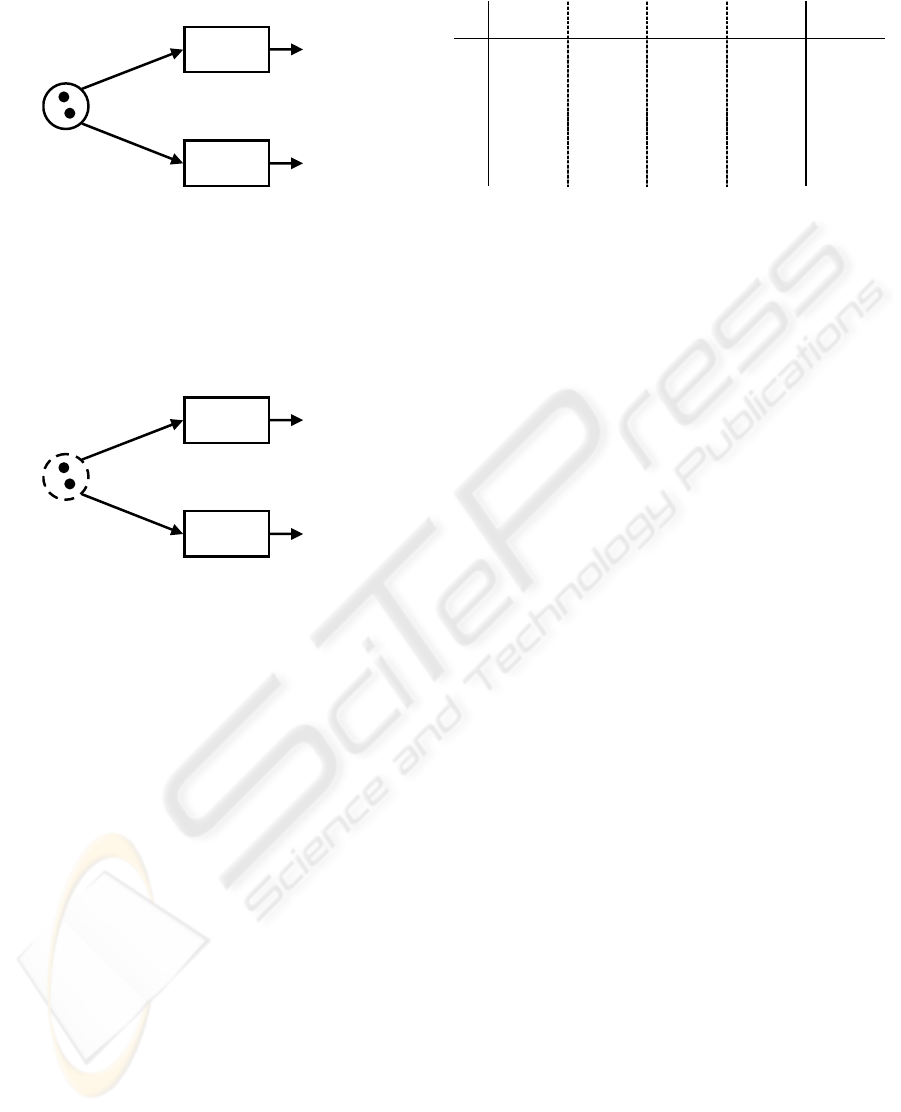
sufficient information to route all tokens, we say that
the input place belongs to the lower approximation.
…
…
Flu=yes
Flu=no
A
B
Figure 4: A Place in a Lower Approximation.
Now, let us consider that a routing decision
cannot be made by the OR-split for at least one
token. In such circumstances we define the input
place as member of an upper approximation. This
indicates that the decision rule of the OR-split is
fragmentary.
…
…
Flu=yes
Flu=no
A
B
Figure 5: A Place in an Upper Approximation.
To graphically distinguish between places
belonging to a lower and upper approximation we
introduce a "dashed circle" place notation as
depicted in
Figure 5 (in contrast to a solid perimeter
as in Figure 4).
Note that this concept can be easily extended to
more general OR-splits, e.g. a three way dispatcher
where one way can be excluded and the remaining
two are possible.
3.2.4 Relationship between Rough Tokens
and Places
On the first sight the relationship between rough
tokens and rough places seems to be fully
symmetric. However consider the extended patient’s
decision table as depicted in Table 2. It now contains
the new attribute dysgeusia.
Table 2: Extended Patient’s Decision Tree.
# Temp-
erature
Head-
ache
Nausea Dysge-
usia
Deci-
sion
1. high yes no yes yes
2. v_high yes yes yes yes
3. high no no no no
4. high yes yes yes yes
5. high yes yes no no
6. normal yes no no no
7. normal no yes no no
8. normal yes no no yes
The decision set is a sub-set of the set of
attributes provided by the patient. Let us consider
the two pairs of patients (#4, #5) and (#6, #8) that
had contradicting information in Table 1.
If we keep the decision set as defined before, the
results remain unchanged. The pairs (#4, #5) and
(#6, #8) are still indiscernible. However since we
only take a sub-set of the possible decision set, we
consider the “problem” as a problem of the place. So
the tokens might be discernible if all attributes are
taken into account.
Actually, the complete decision set delivers an
improved result. The formerly indiscernible patients
(#4, #5) can now be correctly diagnosed with the
additional information (attribute dysgeusia), while
the patients (#6, #8) are still indiscernible.
In summary, the first case would deal with rough
places and the second with rough tokens.
3.2.5 Rough Routes
The analysis of rough routes is a generalization of
global view on the concept of rough places as
discussed in Section 3.2.3.
A route through a net is only determinable when
it consists only of places in lower approximations.
As soon as there is one place in a upper
approximation the route through the net cannot be
determined without any additional information.
Therefore the route gets rough from this place
onwards.
So only for those nets with routes in lower
approximations can one be sure that the tokens
require no additional information to reach the end
place.
ICEIS 2007 - International Conference on Enterprise Information Systems
438

4 POTENTIAL APPLICATION IN
PRACTICE
4.1 Early Warning of Incomplete Case
Information
The main area of application of the proposed method
is to provide early warning of potential delays within
the workflow that could be caused by incomplete
information in certain business cases.
The aim would be to get the workflow system to
alert the end user when a choice is waiting on more
information. In the local case, the next transition will
be held up. In the global case, the alert is a warning
that further down the track, a transition may be held
up.
Ideally, the workflow system should monitor the
arrival of the required extra data, so that transitions
can be automatically enabled without user
intervention. This may well involve facilities to set
up software agents that can talk to the applications
that manage this data.
If, however, it can be seen in advance that certain
combinations of case attributes mean that a choice
cannot be resolved, the workflow template should
probably be altered to allow for a "don't know"
branch. The process owner would need to define
how long cases can be left in this state, and what
should happen to them when time runs out.
4.2 Extending Workflow Models
Workflow management systems mostly depend on a
paradigm in which individual business cases follow
templates that are specified in some description
language similar to a Petri net.
These process modelling tools all depend on a
combination of simple diagrams and property sheets
to capture process templates. They allow the
specification of a number of "case attributes" in their
template property sheets. Attribute values for each
case are provided at run time, either by a human
participant or an associated application.
A combination of case attributes corresponds to
the colour of tokens in the coloured Petri net sense.
The conditions for branching one way or another at a
decision point are expressed as properties of the
outgoing edges of a decision node. If incomplete
information implies that the business case can not
continue, one option would be to introduce a “wait
for data” activity with a loop back to the beginning
of the decision node. However it has to be
acknowledged that adding more complexity in
process model diagrams can be counter-productive.
At run time, some workflow systems offer the
end-user a graphical view of the whole of the current
business case. In Chameleon (O'Hagan, 2005) for
instance, a colour coding of activities in the whole
process is used as follows:
Pink, activities that are already completed
Green, activities currently being worked on
Blue, further activities available to this user
Yellow, activities not yet available, or not
required.
Although Chameleon models do not strictly
follow Petri net conventions, it would be
theoretically possible to introduce further colour
coding to indicate where incomplete information
threatens to hold up the workflow, either at just the
next decision point or later on, for each business
case.
5 CONCLUSIONS
In this paper we have introduced the fundamental
ideas of rough set theory and showed its potential
use for the management of missing or incomplete
information in workflow systems.
The main purpose is to utilize rough set theory to
make incomplete information visible in order to deal
with such a situation proactively.
Our future research will concentrate on a more
formal incorporation of these concepts into
workflow management.
REFERENCES
Bargiela, A. & Pedrycz, W. (2002), Granular Computing:
An Introduction, Kluwer Acamemic Publishers,
Boston, MA, USA.
Dubois, D. & Prade, H. (1990), 'Rough Fuzzy Sets and
Fuzzy Rough Sets', International Journal of General
Systems 17, 191-209.
Fowler, F. (2003), UML Distilled: A Brief Guide to the
Standard Object Modeling Language, Addison-
Wesley Professional, Boston, MA, USA.
Grzymala-Busse, J. (2004), Introduction to Rough Set
Theory and Applications, in 'KES2004 - 8th
International Conference on Knowledge-Based
Intelligent Information & Engineering Systems'.
Hoffmann, F.; Koeppen, M.; Klawonn, F. & Roy, R., ed.
(2005), Soft Computing: Methodologies and
Applications, Vol. 32, Springer Verlag, Berlin,
Germany.
MAKING INCOMPLETE INFORMATION VISIBLE IN WORKFLOW SYSTEMS
439

Komorowski, J.; Pawlak, Z.; Polkowski, L. & Skowron,
A. (1999), Rough Sets: A Tutorial, in S. K. Pal & A.
Skowron, ed., 'Rough-Fuzzy Hybridization: A New
Trend in Decision Making', Springer-Verlag,
Singapore, 3-98.
Lingras, P. & West, C. (2004), 'Interval Set Clustering of
Web Users with Rough K-Means', Journal of
Intelligent Information Systems 23, 5-16.
Mitra, S. (2004), 'An Evolutionary Rough Partitive
Clustering', Pattern Recognition Letters 25, 1439-
1449.
Murata, T. (1989), 'Petri Nets: Properties, Analysis and
Applications', Proceedings of the IEEE 77(4), 541-
580.
O'Hagan, T. (2005), Chameleon Workflow Demos,
University of Queensland website,
http://www.itee.uq.edu.au/~tohagan/Chameleon/
Pawlak, Z. (1982), 'Rough Sets', International Journal of
Information and Computer Sciences 11, 145-172.
Pawlak, Z. (1992), Rough Sets: Theoretical Aspects of
Reasoning about Data, Kluwer Academic Publishers,
Boston, MA, USA.
Peters, G. (2006), 'Some Comments on Rough Clustering',
Pattern Recognition 39(8), 1481-1491.
Peters, J.F.; Skowron, A.; Suraj, Z. & Ramanna, S. (1999),
Guarded transitions in rough Petri nets, in 'Proceed.
EUFIT99 - 7th European Congress on Intelligent
Systems & Soft Computing'.
Peters, J.F.; Skowron, A.; Suraj, Z.; Ramanna, S. &
Paryzek, A. (1998), Modeling real-time decision-
making systems with rough fuzzy Petri nets, in
'Proceed. EUFIT98 - 6th European Congress on
Intelligent Techniques & Soft Computing', pp. 985-
989.
Peters, J.F.; Ramanna, S.; Suraj, Z. & Borkowski, M.
(2003), Rough Neurons: Petri Net Models and
Applications., in A. Skowron S.K. Pal, L. Polkowski,
ed.,' Rough-Neuro Computing', 472-491.
Peters, J.F.; Skowron, A.; Suray, Z. & Ramanna, S.
(2000), Sensor and Filter Models with Rough Petri
Nets, in H.D. Burkhard; L. Czaja; A. Skowron & P.
Starke, ed., 'Proceedings of the Workhop on
Concurrency, Specification and Programming',
Humboldt-University, Berlin, 203-211.
Polkowski, L.; Skowron, A. & Komorowski, J. (1996),
Approximate case-based reasoning: A rough
mereological approach, in 'Proceed. 4-th German
Workshop on Case Based Reasoning, System
Developments and Evaluation', pp. 144-151.
Polkowski, L. (2003), Rough Sets, Physica-Verlag,
Heidelberg, Germany.
Scheer, A. (2000), ARIS - Business Process Modeling,
Springer-Verlag, Berlin, Germany.
Skowron, A. & Swiniarski, R. (2001), Rough Sets in
Pattern Recognition, in Pal, S.K. and Pal, A., Pattern
Recognition: From Classical to Modern Approaches,
World Scientific, Singapore, pp. 385-425.
Slowinski, R. (1993), Rough set learning of preferential
attitude in multi-criteria decision making, in J.
Komorowski & Z. Ras, ed., 'Methodologies for
Intelligent Systems', Springer-Verlag, Berlin,
Germany, pp. 642-651.
Suraj, Z. (2000), Rough set methods for the synthesis and
analysis of concurrent processes, in Polkowski, L. and
Tsumoto, S. and Lin, T., Rough set methods and
applications: new developments in knowledge
discovery in information systems, Physica-Verlag,
Heidelberg, Germany, pp. 379-488.
van der Aalst, W. & van Hee, K. (2002), Workflow
Management - Models, Methods, and Systems, MIT
Press, Cambridge, MA, USA.
van der Aalst, W. (1999), 'Formalization and Verification
of Event-driven Process Chains', Information and
Software Technology 41(10), 639-650.
van Hee, K.; Oanea, O. & Sidorova, N. (2005), Colored
Petri Nets to Verify Extended Event-Driven Process
Chains, in ' Proceed. CoopIS 2005 - 13th International
Conference on Cooperative Information Systems', pp.
183-201.
Yao, Y.; Li, X.; Lin, T. & Liu, Q. (1994), Representation
and Classification of Rough Set Models, in
'Proceedings Third International Workshop on Rough
Sets and Soft Computing', pp. 630-637.
Zadeh, L. (1965), 'Fuzzy Sets', Information and Control 8,
338-353.
Zimmermann, H. (2001), Fuzzy Set Theory and its
Applications, Kluwer Academic Publishers, Boston,
MA, USA.
ICEIS 2007 - International Conference on Enterprise Information Systems
440
