
UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF
DETAIL RENDERING OF BINTREE TRIANGULATIONS
Bernd Biedermann and María Cecilia Rivara
Departamento de Ciencias de la Computación, Universidad de Chile, Chile
Keywords: Bintree Triangulations, Parallel Mesh Tessellation, Continuous Level of Detail, Uncoupled Parallel Mesh
Refinement.
Abstract: In this paper we present an uncoupled parallel technique for view dependant continuous level of detail
rendering of regular height field terrain. To this end, the terrain is globally modelled by a simple bintree
patch-based representation of right-triangles, which is adaptively divided into uncoupled meshes for parallel
processing. This is easily performed by uncoupling the mesh along the observer line. Each uncoupled mesh
is then recursively approximated to the corresponding level of detail in the terrain. Cracks are avoided by
constraining the refinement levels at the boundaries of adjacent meshes. The level of detail is created on-
the-fly with a low amount of CPU overhead, allowing a good representation of the terrain and high frames
per second performance. This implementation shows significant improvements in CPU load and frames per
second performance over the serial method when executed on machines with multiple processors.
1 INTRODUCTION
Several approaches for multiresolution
representation, adaptive modelling, level of detail
control, and real time rendering of terrain data have
been proposed and studied in the last 10 years.
Pioneer work on general mesh simplification and
multiresolution modelling are discussed in (Heckbert
and Garland 1997; Hope 1996, Hope 1998). In
particular for the multiresolution modelling of
regular height-field data, methods based on right-
triangle triangulations have been developed and
widely used. The most important of these methods
are quadtree-based and bintree-based representations
methods (Duchaineau et al, 1997; Pajarola 2002).
These methods are reported to provide a more
compact representation of the terrain, better spacial
access, faster level of detail (LOD) triangulation and
rendering and are easier to implement than more
general methods. (Pajarola 2002).
Recently (Holst and Schumann 2006) combine
the use of a reduced multiresolution hierarchy based
in (De Floriani et al 1997) together with triangle
strips for patches. They do not use right bintree
triangle representation, nor perform any parallel
work.
As a basic tool of this research we use a right-
triangle multiresolution bintree algorithm as
discussed in (Duchainean et al, 1997), which is a
special case of the longest edge refinement
algorithms for general triangulations discussed in
(Rivara 1984, Rivara 1997).
Essentially, the bintree multiresolution method
works as follows: (1) Each right triangle in the
bintree structure is splitted by its longest edge
producing right and left right-triangle children in the
bintree; (2) The adaptive local splitting of every
target triangle is performed by using a sequence of
simple mesh operations over couples of triangles of
the same bintree level, which share a longest edge in
the mesh; (3) The local splitting of a general target
triangle having a longest-edge neighbour of a
different level requires splitting propagation, which
is a particular case of the longest edge propagation
path discussed in (Rivara 1997).
When rendering terrain a specific problem arises.
The horizon of visibility is much bigger than in other
real time rendering with fixed scenes. If we were to
render every triangle at a fixed resolution we would
either have a very low quality terrain or a low
performance with a high quality terrain. To solve
this particular problem the amount of triangles close
to the observer has to be maximized and be reduced
as the distance increases. This is known as
continuous level of detail and the problem has been
333
Biedermann B. and Cecilia Rivara M. (2007).
UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF DETAIL RENDERING OF BINTREE TRIANGULATIONS.
In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 333-338
DOI: 10.5220/0002083203330338
Copyright
c
SciTePress
addressed by some authors with different techniques.
The core of the problem is to find a mesh for each
frame that will realistically represent the terrain. The
main problem of Continuous Level of Detail is the
huge amount of CPU overhead it produces. The
ROAM (Real Time Optimally Adapting Meshes)
algorithm (Duchaineau et al, 1997), which will be
briefly explained on this paper, is a View Dependant
Level of Detail algorithm, which adapts a mesh to an
optimal triangulation for the camera point of view.
In order to improve the adaptive terrain
rendering performance we propose a parallel
uncoupled method similar to the one discussed in
(Rivara et al, 2006) which takes advantage of the
multiprocessor architecture of current computers.
Traditional VLOD (Visual dependant Level of
Detail) algorithms run all this CPU work through
only one processor and therefore make the CPU
overhead a big problem. This can be reduced by
mesh subdivision and parallel tessellation (Padrón et
al, 2005). Most algorithms present fairly
complicated solutions for this. In this paper we
consider simple parallelization of real time view
dependant continuous level of detail.
2 BASIC TECHNIQUES USED IN
THIS PAPER
2.1 View Dependant Level of Detail
Algorithms
VLOD algorithms are designed to interactively
perform view-dependent locally adaptive terrain
meshing. They rely on a multi-resolution terrain
representation that is used to build the adaptive
terrain representation of a frame. To accomplish this,
the algorithm used in this paper is a basic
implementation of ROAM. VLOD algorithms take
the complete terrain data usually, in form of a height
field, and generate a mesh that includes every vertex
of the height map near the observer and discard
vertices as they generate mesh sections further away
from the observer. ROAM accomplishes this by
generating a mesh for each frame, while other
algorithms, like GeoMipMaps (H. de Boer, 2000
) do
this by pre-calculating a certain amount of meshes.
The advantage of dynamically generating the mesh
for each frame is that the representation is much
better than on pre-calculated meshes. The
disadvantage is that they require a lot more
processing than pre-calculated meshes do. To make
up for this a simple parallelization mechanism is
shown in this paper.
2.2 Mesh Representation
Multiresolution representations based on right-
triangle triangulations are the most suitable for
adaptive terrain modelling of regular height field
data, where a multi-resolution surface is stored in a
data structure that can be recursively refined on
demand. Among these we can mention the quatree
and bintree methods (Lario, Pajarola and Tirado,
2003). Quad-Trees have the disadvantage though,
that they are inherently based on recursive quads
which can have up to four children. For our purpose
a structure that is inherently based on triangles is
much better suited given the refinement technique
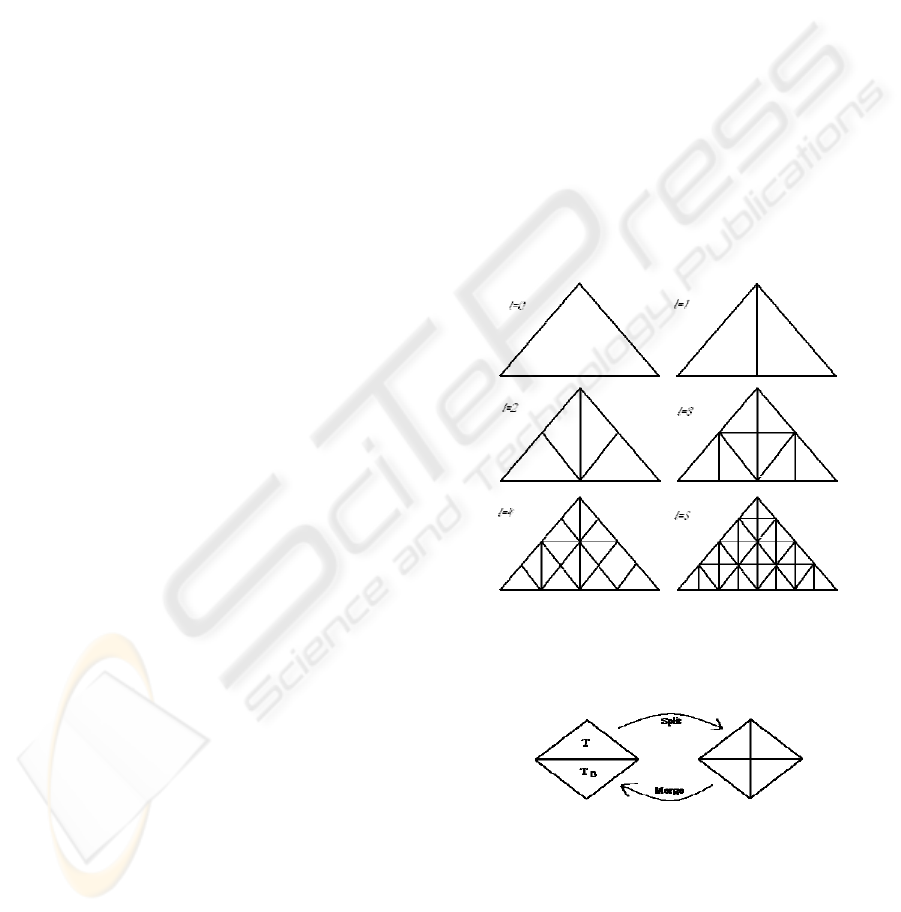
described later. In a Binary Triangle Tree, each of
two possible children are triangles formed by
dividing the parent triangle in two by longest edge
bisection as illustrated in Figure 1. For a discussion
and evaluation of the bintree multiresolution
representation see (Duchaineau et al, 1997; Pajarola
2002).
Figure 1: First 6 levels of a Binary Triangle Tree.
Figure 2: Split and Merge operations.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
334
3 NON-PARALLEL BINTREE
PATH-BASED METHOD
The serial method chosen to represent terrain is a
simple version of ROAM. The algorithm can be
described as follows:
Serial Tessellation Algorithm:
Input: A high resolution height map terrain data.
a) The terrain data is divided into N square patches.
b) Each terrain patch is initialized with two bintree
triangle structures at the coarsest level (every patch
contains two triangles). The height coordinate of
each triangle vertex is given by the corresponding
value in the height map.
c) All triangles are linked together by pointers to
their three neighbours.
For each frame adaptively do:
d) The landscape is initialized and the adaptive
view dependant level of detail tessellation process
is performed.
e) The frame is rendered.
For ends.
The terrain is subdivided into bintree patches in
order to keep the depth of the tree structures
controlled.
During the tessellation process (Duchaineau et
al, 1997) the mesh is dynamically calculated for
each frame. This is done by recursively traversing
the two BTT structures in each visible patch and
refining it until the desired level of detail is reached.
This is done with two basic mesh operations called
merge and split (see figure 2).
When two adjacent triangles are both from the
same level we refer to it as a diamond. Split replaces
a triangle T with its children T0 and T1 and does so
with the adjacent triangle as well. This introduces a
new vertex at the centre of the diamond, resulting in
a new continuous triangulation.
This tessellation process is by far the most CPU
expensive part of the algorithm. During this process,
each visible patch is visited and their BTT structures
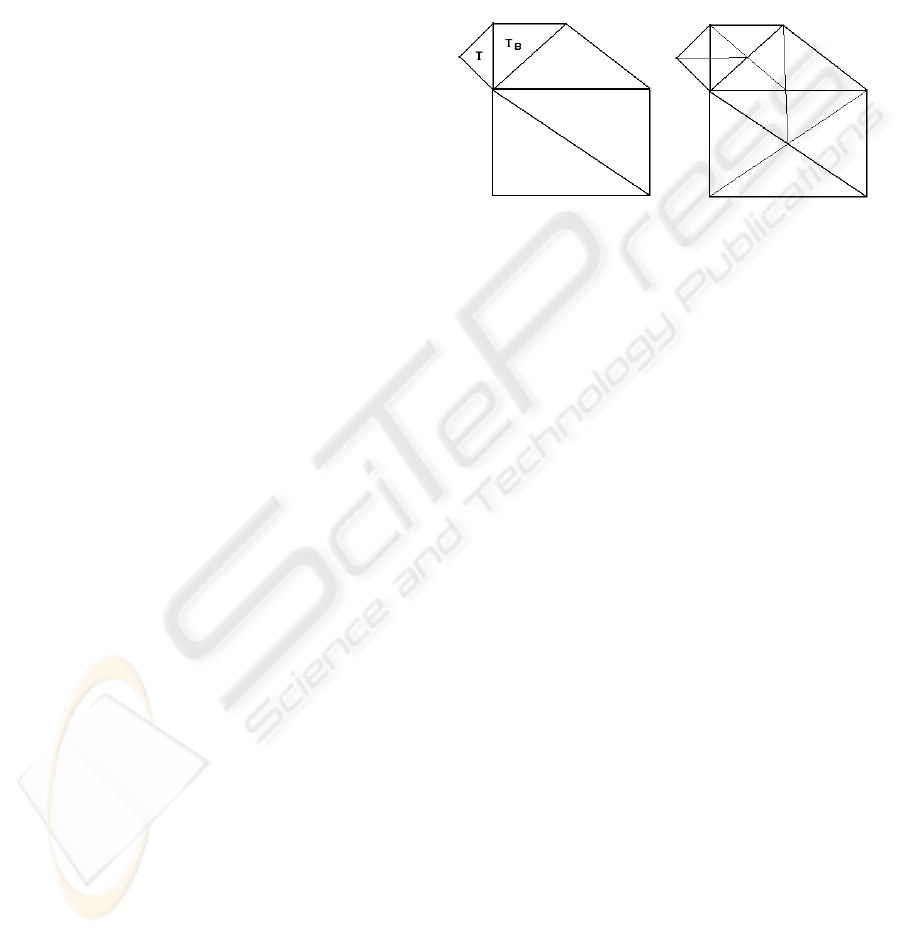
recursively traversed and refined. A triangle T in a
triangulation cannot be split immediately when its
base neighbour Tb is of a coarser level. It would
produce a crack in the mesh, so we have to force T
to split. To force T to split, Tb must be forced to
split first, which may require other triangles to split
first. As long as we recursively split all required
triangles, the mesh will remain consistent. This is
also known as the Longest Edge Propagation Path or
LEPP (Rivara, 1997), which finishes finding a
terminal edge, which is the base edge for two
adjacent triangles or an edge of the border of the
mesh. Only then we start the splitting process (see
figure 3).
If we go on refining too much, we can eventually
run out of memory. To avoid this, a pool of possible
vertices to be allocated is defined. Once a new
vertex is introduced, it is eliminated from the pool
and becomes part of the triangulation. Once we run
out of vertices in pool, no further refinement is
possible.
Figure 3: In order to split T all the triangles along the
longest edge path have to be split first.
Since we want different levels of refinement on
different areas of the mesh, we need to decide how
far to refine the mesh in a given point. This is done
by introducing an adaptive tolerance parameter t
which depends on the distance of the given point to
the observer.
Each time that a triangle in the BTT is analyzed
we compute t for the given position and compare its
value with the distance between the middle point of
the triangles base and the corresponding point in the
Height Map. If the distance is bigger than our
calculated t we split the triangle. In this way we
achieve our goal of continuous level of detail.
4 PARALLEL TESSELLATION
With multiple processor technology the tessellation
could be done in a fraction the time if the meshing
problem is decoupled. The problem that arises is that
given the recursive nature of the process, the CPUs
might want to allocate the same vertex at the same
time, causing access violations and ending the
process. The first approach to solve this problem is
to work on separate meshes and thereby distributing
the process completely. This causes a problem of
continuity at the bounding of adjacent meshes. For
illustration purposes, let us focus on dual processor
scenario. As both meshes are refined independently,
we have no guarantee the union is going to be
continuous and therefore cracks may appear at the
union.
UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF DETAIL RENDERING OF BINTREE
TRIANGULATIONS
335
Other algorithms solve the problem by
concurrent vertex insertion (Chernikov and
Chrisochoides, 2004), scheduling the point insertion
in such a way that no access violations will occur
during the refinement. The problem could be solved
by using a different mesh structure but we want to
keep the efficiency of the BTT structure. The
solution implemented in this paper works by
decoupling the mesh, and working on it as if it were
two separate meshes, but maintaining consistency.
This way we do transform the process into a
distributed problem but with shared memory
resources.
The solution implemented parallel tessellation
algorithm works as follows:
Input: a high resolution height map terrain data.
The terrain data is divided in N square patches.
Each terrain patch is initialized with two bintree
triangle structures.
While the observer traverses the terrain do
For each frame (observer position) do
- the mesh is partitioned along the observer line L
and common parameters t are calculated along L.
- each submesh and associated parameters t are
assigned to each processor for tessellation.
- each submesh is adaptively calculated in parallel
using bintree triangle structures until the desired
level of detail is achieved.
For ends.
While ends.
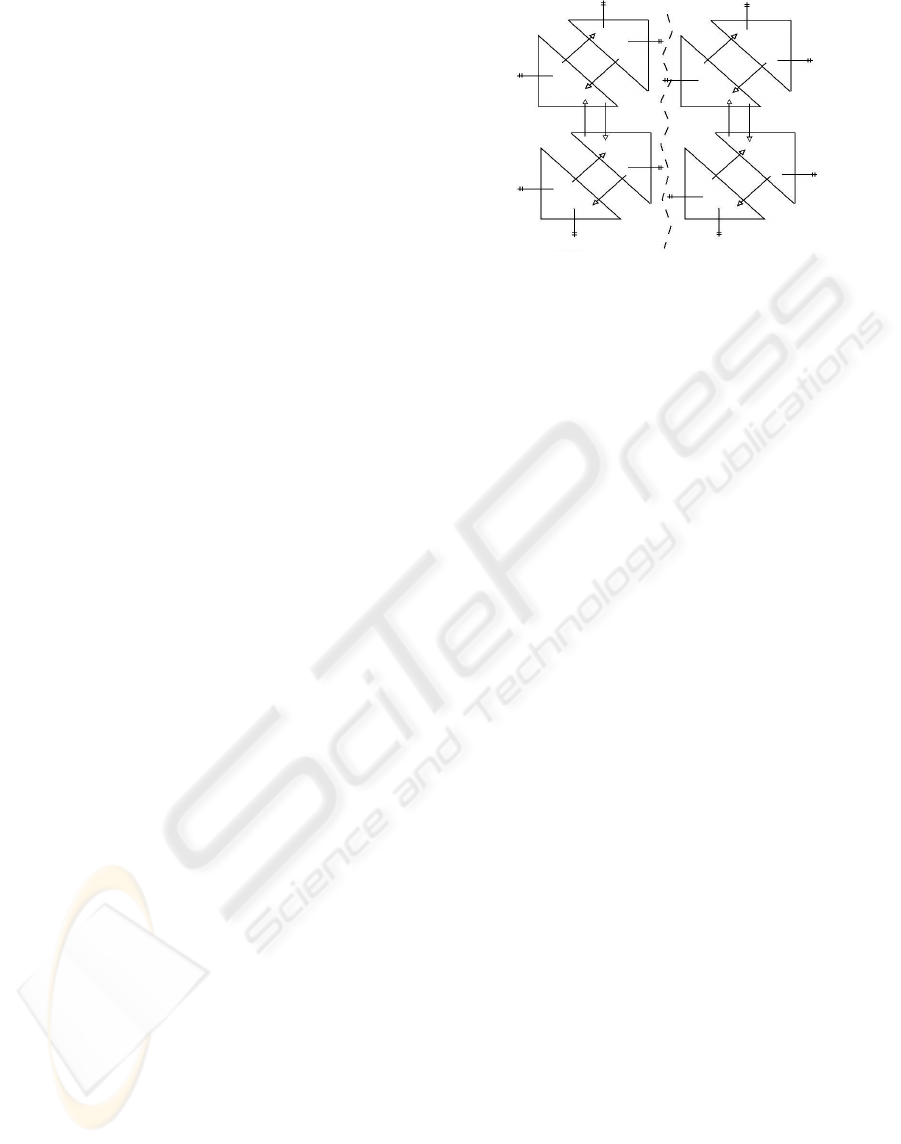
The reason to partition the mesh along the line of
observation is to balance processor load. This can be
easily done by identifying the patches at each side of
the observer and accessing their BTT structures.
At the initialization stage all triangles of the BTT
structures would be linked together in the serial
algorithm, instead each half of the mesh is linked
together, leaving an unconnected division of it
running through the middle of the mesh (see figure
4). This way we assure that it is a decoupled
problem because the edges in the middle of the mesh
become terminal edges, were the refinement stops.
More on decoupled parallel refinement can be found
in (Rivara et al, 2006).
After splitting the mesh two separate pools for
vertex allocation are defined. This way both halves
can be refined independently without sharing
resources.
The LOD is computed by two tessellation
threads. These can be assigned to separate CPUs.
The tessellation process is the same as in the non-
parallel case using the method described above.
Each of the tessellation threads has its own pool
of vertices and set of patches containing the BTT
structures, the only shared resource is the height
map. If we would duplicate the height map and
include a copy of the height map to each thread, the
process would be completely distributed and
therefore have no shared memory resources. This
could be useful to run the algorithm on a cluster of
machines.
For the parallel processor problem, the access to
the height map does not present any problems,
because each thread is dealing with a different part
of the terrain and therefore there is no possibility
that both threads would try to access the same value.
Once the tessellation process is complete, and
before the rendering step can start, the two halves
have to be consistent with each other to avoid cracks
at the initial division line of the mesh. At this point
we have no guarantee that both parts of the meshes
fit together without leaving cracks at the union. To
ensure consistency we force the tolerance factor t at
both adjacent borders to be exactly the same. This
means the same level of detail will be used on both
halves and the condition to stop refining is the same
at both sides of the union as long as we had enough
vertices in the pool. This produces a mesh with
duplicate vertex at the union and thus producing a
few extra triangles, but with no cracks in the mesh.
We are also over-refining the neighbouring mesh.
This causes a few extra triangles to appear at the
coarser side of the mesh. The triangle overhead is a
small price to pay, given the fact we have done the
tessellation in almost half the time.
5 RESULTS
To test the performance of the algorithm, a parallel
version and a non-parallel version of the same
algorithm were implemented and compared in terms
of CPU load, memory usage and frames per second
performance.
The testing method used can be described as
follows. A 230 second long flight over the terrain
Figure 4: The initial mesh is divided. The triangles
running along the middle are uncoupled.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
336

was programmed and executed ten times. Each of
the flights was done rendering the scene at different
levels of detail, starting with 180000 vertices and
ending at 5000. Each flight was performed with the
serial and the parallel algorithm and CPU load and
frames per second were measured for both
algorithms. The number of desired vertices per
frame, maximum allowed time and circuit were
given. Spatial steps were calculated in terms of the
elapsed time, total time allowed and position. The
test platform was a dual Turion64 processor
computer, running at 1.6 GHz with 1 GB of RAM
and an Nvidia GeForce 6100 graphics card running
Windows XP.
The results are illustrated in the following table:
Table 1: Performance of sequential and parallel algorithm.
Vertices
per
Frame
Average
Sequential
frames/sec
Average
Parallel
frames/sec
% Increase
in
Performance
180000 17.03 23.78 39.64
160000 17.42 25.31 45.29
140000 20.22 33.10 63.70
120000 21.05 35.71 69.64
100000 23.61 39.85 68.78
80000 28.60 44.57 55.84
60000 39.42 57.35 45.48
40000 52.19 68.16 30.60
20000 71.04 73.06 2.84
5000 81.03 81.18 0.19
The same experiment executed over different
terrain data yielded similar results.
As shown in figures 6 to 8, the average CPU
load was well balanced. The load balance was not
exactly the same due to differences on the terrain
geography on each side of the mesh division.
Although one might be tempted to think that the
performance should increase by a bigger factor, we
need to have in mind the fact that all we have done
is parallelizing the tessellation process, but other
processes like computing texture coordinates are
done sequentially. Given this, the increase in frames
per second performance shown in table 1 is
considerable. As shown in table 1, the increase in
performance was at its maximum between 100 000
and 160 000 vertices per frame. When decreasing
the amount of vertices, the parallel algorithm shows
smaller improvement over the sequential algorithm.
This happens because at low workloads one CPU is
able to manage all of the work, improvement starts
to be noticeable at 40 000 vertices. On the other end,
with over 160 000 vertices the improvement of the
parallel algorithm over the sequential one starts
decreasing until it stays at around 39 %.
The memory usage showed no considerable
change between the serial and the parallel algorithm.
In both algorithms the entire structure could be
stored in the same amount of memory. This was to
be expected as the mesh size did not change and no
extra storage space was needed. The structure took
about 1.2 MB of storage space at low vertex rates.
This increased to a maximum of 17.2 MB at 180 000
vertices per frame.
Figure 6: CPU load at 180 000 vertices per frame.
Figure 7: CPU load at 100 000 vertices per frame.
Figure 8: CPU load at 20 000 vertices per frame.
Figure 5: Terrain mesh.
UNCOUPLED PARALLEL VIEW DEPENDANT LEVEL OF DETAIL RENDERING OF BINTREE
TRIANGULATIONS
337

6 CONCLUSIONS AND
DISCUSSION
We have presented a parallel continuous level of
detail technique for rendering bintree based
structures. The mayor improvements in performance
are achieved by turning the problem into an
uncoupled refinement process, which allows a
terrain mesh to be generated on multiple processors
and thereby increasing the performance in terms of
frames per second considerably.
The issue of keeping the load balanced on more
than two processors posts some difficulty because
the mesh partitioning strategy needs to be
generalized. Due to the decreasing level of detail
towards the observers horizon, and the changes in
complexity of the mesh, the next partition strategy is
much harder to determine and will be part of future
research.
This paper focused on showing the increase in
performance by parallel mesh tessellation, but many
improvements can still be implemented, like node
caching, triangle fan generation, priority queues and
occlusion culling among other techniques.
ACKNOWLEDGEMENTS
This work was partially funded by Fondecyt
1040713. We are also grateful to the referees whose
comments contributed to improve this paper.
REFERENCES
Mark Duchaineau, MurrayWolinsky, David E. Sigeti,
Mark C. Miller, Charles Aldrich, Mark B. Mineev-
Weinstein, ROAMing Terrain: Real-time Optimally
Adapting Meshes In Roni Yagel and Hans Hagen,
editors, IEEE Visualization '97, pages 81--88. IEEE
Computer Society Press, Los Alamitos, CA,
November 1997.
Willem H. de Boer, Fast Terrain Rendering Using
Geometrical MipMapping E-mersion Project,
http://www.connectii.net/emersion, October 2000
E. J. Padrón, M. Amor, M. Bóo, R. Doallo, Efficient
Parallel Implementations for Surface Subdivision. In
Fourth Eurographics Workshop on Parallel Graphics
and Visualization, Pages: 113 - 121 (2002)
Andrey N. Chernikov, Nikos P. Chrisochoides, Practical
and Efficient Point Insertion Scheduling Method for
Parallel Guaranteed Quality Delaunay Refinement. In
Proceedings of the 18th annual international
conference on Supercomputing, Pages 48-57 2004
Martin Bokeloh, Michael Wand, Hardware Accelerated
Multi-Resolution Geometry Synthesis. In Proceedings
of the 2006 symposium on Interactive 3D graphics and
games, Pages 191-198
Joshua Levenberg, Fast view-dependent level-of-detail
rendering using cached geometry. In Proceedings of
the conference on Visualization 2002, Pages 259-266
María Cecilia Rivara, Using Longest-Side Bisection
Techniques for Automatic Refinement of Delaunay
Triangulations. In International Journal for Numerical
Methods in Engineering 1997, Pages 581-507
Renato Pajarola, Overview of Quadtree-based Terrain
Triangulation and Visualization. In Technical Report
UCHCS-02-01, Information and Computer Science,
University of California, Irvine, 16 pages, 2002
M.C. Rivara, C. Calderon, A. Fedorov, N. Chrisochoides,
Parallel Decoupled Terminal-Edge Bisection Method
for 3D Mesh Generation. In Engineering with
Computers, 22(2): Pages 111-119, 2006
Hugues Hoppe. Smooth view-dependent level-ofdetail
control and its application to terrain rendering. In
Proceedings Visualization 98, pages 35–42. IEEE,
Computer Society Press, Los Alamitos, California,
1998.
H. Hoppe. Progressive meshes. In Proceedings
SIGGRAPH 96, pages 99–108. ACM SIGGRAPH,
1996.
Michael Garland and Paul S. Heckbert. Fast polygonal
approximation of terrains and heigt fields. Technical
Report cmu-cs-95-181, School of Computer Science,
Carnegie Mellon University, Pittsburgh, PA, 1995.
Mathias Holst and Heidrun Schumann. Efficient
Rendering of High –Detailed Objects Using a Reduced
Multi-Resolution Hierarchy. In Proceedings of
GRAPP 2006, Pages 3-10.
Leila De Floriani, Paola Magillo, and Enrico Puppo.
Building and traversing a surface at variable
resolution. In proceedings of the 8
th
conference on
visualization 1997, pages 133-ff. IEEE Computer
Society Press.
Peter Lindstrom and Valerio Pascucci. Visualization of
Large Terrains Made Easy. In Proceedings of the
conference on Visualization 2001,Pages 363-371.
GRAPP 2007 - International Conference on Computer Graphics Theory and Applications
338
