OUT OF CORE CONSTRUCTION OF PATCH TREES

Hermann Birkholz

Institute for Informatics, University of Rostock, Albert-Einstein Street 21, 18059 Rostock, Germany

Keywords: Out of Core, Patch Tree, Level of Detail.

Abstract: Current Level of Detail (LoD) approaches for triangle meshes use variably triangulated mesh patches in

order to approximate the original mesh surface. The approximation is synthesized from some of these

patches, which have to cover the whole surface and must not intersect each other. The patches are chosen

corresponding to the necessary view dependent triangulation. This paper addresses the creation of the re-

quired hierarchical data structures, in order to enable Level of Detail synthesis for very large triangle

meshes. Because of the limited amount of internal memory, most of the mesh data reside in external mem-

ory during the process. Due to the high access latency of external memory, commonly used algorithms for

small meshes are hardly applicable for so called “Out of Core” meshes. Other methods have to be found that

overcome the problems with the external memory.

1 INTRODUCTION

Widely available massive triangle meshes that are

for instance results of highly detailed laser scans,

demand special algorithms in order to explore them

interactively.

Due to its size the complete data set does not fit

into the internal memory of current PC hardware.

Thus, only parts of the mesh can be used for a real-

time exploration, while most of the data have to re-

main in external memory. This demands fast swaps

between external and internal memory.

Thus, interactive Level of Detail (LoD) algo-

rithms use mesh patches, in order to synthesize ap-

proximations of the original mesh. These mesh

patches have different levels of detail and can be

merged into a mesh which covers the complete sur-

face of the original mesh.

This paper describes the creation of the neces-

sary data structures for a patch-based LoD algorithm

in external memory. Due to the speed limitations of

external memory devices, the process is serialized as

much as possible and uses efficient caching.

First, a short selection of related articles is given

in the next section. The third section describes the

usage and the creation of so called “patch trees”,

which enable a patch based LoD synthesis. Finally

some results an a short conclusion are given in the

following sections.

2 RELATED WORK

Popular LoD schemas, such as “edge collapse”-

hierarchies for arbitrary meshes (Hoppe, 1997) or

ROAM for height-field meshes (Duchaineau, 2001)

are normally used with small data sets and have a

very fine granularity. For these examples, the granu-

larity for LoD operations is two triangles and creates

a high CPU load during mesh updates. Furthermore,

memory swap operations are very inefficient for

such a fine granularity, because external memory

operations are only efficient for larger blocks of

memory and sequential access.

In (Hoppe, 1998) an “Out-of-Core” terrain ren-

dering system is presented, that creates a Progressive

Mesh in external memory. Therefore the terrain map

is divided into blocks, which are independently sim-

plified (borders must not be changed). After that,

these blocks are merged and simplified again, until

only one block remains. The externally stored “edge

collapse”-hierarchy is used to approximate the origi-

nal terrain data set.

Newer approaches (Cignoni, 2003, 2004, 2005)

use mesh patches to assemble the mesh approxima-

tion. The first approach uses the ROAM hierarchy

together with a batched height-field mesh, while the

second approach can also be used for arbitrary

meshes. The third approach generalizes the MT-

hierarchy (Puppo, 1996) data structure for the use

with patches. The patches in these approaches con-

tain many triangles and thereby increase the granu-

153

Birkholz H. (2007).

OUT OF CORE CONSTRUCTION OF PATCH TREES.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 153-158

DOI: 10.5220/0002081801530158

 SciTePress

larity of the LoD algorithm. This also reduces the

necessary hierarchy structure that stores how patches

can be substituted. Such smaller hierarchy structures

furthermore reduce the CPU-load during mesh up-

dates.

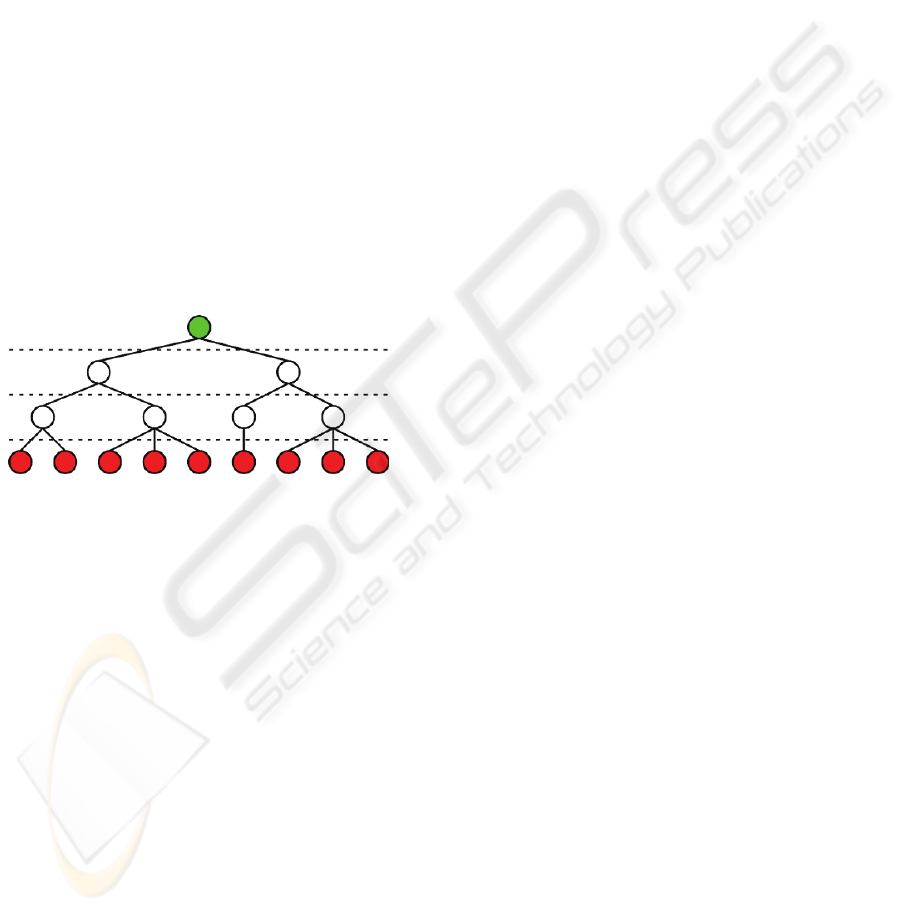
3 PATCH TREES

A patch tree is a data structure that describes the

surface of a triangle mesh with different levels of

detail. All nodes of the tree contain compact mesh

patches, which are used to synthesize view depend-

ent approximations of the original mesh. The leaf

nodes contain the original geometry of the mesh,

while parent nodes always contain a simplified ver-

sion of the geometry of their child nodes.

In the context of this paper, the tree is con-

structed with a number of levels that all cover the

complete mesh surface. This means that all leaves of

the tree share the same level and the path length of

all leaf nodes to the root is equal. Figure 1 shows an

example of a typical patch tree.

Figure 1: Simple patch tree structure.

Such patch trees can be used to create approxima-

tions of the original mesh with a restricted cut across

the tree. The cut is constrained to prevent adjacent

patches in the approximation that are more than one

level apart. This constraint enables the pre-

computation of the transitions between adjacent

patches in different levels of the tree.

3.1 Out of Core Creation

The creation of patch trees for very large triangle

meshes, which do not fit into the internal memory, is

very challenging. Due to the evenly distributed ac-

cesses to the surface during the construction of a

patch tree, a direct adoption of standard algorithms

is hardly applicable. Both, the greedy construction of

patches and the surface simplification demand ran-

dom access to the surface data. Due to the high ac-

cess latency of the external memory, most of the

process time would be spent waiting for the external

memory feedback.

In order to reduce the negative effect of external

memory access, intelligent methods have to be used

to reduce random accesses to the surface.

One very important tool to achieve this is the

external heap. This heap enables to serialize many

accesses to external memory by a fast and latency-

optimized sorting of items in the external memory.

Further optimizations can be reached by minimizing

the random accesses to the external memory with

intelligent caching.

The process queue, which is used to create the

patch tree consists of three steps:

 Create leaf patches

 Straighten borders of leaf patches

 Create patch hierarchy

These steps will be further described now.

3.1.1 Create Leaf Patches

In this step, the triangle mesh (indexed mesh) is

segmented into patches. Therefore an average num-

ber of triangles per patch is chosen (e.g. 1000 trian-

gle/patch) and used to determine the number of leaf

patches.

During the creation of the desired number of

patches from the original triangles, all triangles are

treated as patches. First the neighbor-patches of all

triangular patches are determined. Because the mesh

does not fit into internal memory, the process is seri-

alized with external heaps. Therefore all patches are

brought to an external heap, weighted with each of

their vertex indices in ascending order. Now the

patches are read back from the heap, grouped by

equal vertex indices. The neighborhood in each

group is found according to the common vertex in-

dex. After the neighbor has been set, the resulting

triangle is brought to another heap, weighted with

the original triangle index. Now the triangles are

read back from the second heap. Three items are

read from the heap at a time that belong to the same

triangular patch and contain the neighbors. During

the same process, the vertex positions can be associ-

ated with each patch, in order to determine its area

and border segment lengths.

The merge process, which iteratively merges the

two best possible patches into a new patch, cannot

be serialized in the way seen before. Thus the ran-

dom accesses have to be reduced by intelligent cach-

ing. The priority of the merge operations is deter-

mined by the compactness of their results. Each

patch is tested with all adjacent patches and the best

result is chosen as merge-target. The compactness is

measured as circle similarity. The area and the out-

line of the resulting patch is known and thus the

similarity to a circle can be computed. In this ap-

proach, the following measure is used:

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

154

areaoutline

priority

(1)

This measure prefers short outlines such as in

(Sanders, 2001) but also prevents large areas with

small outlines, which could occur on separated fea-

tures such as legs or arms.

The caching is realized with an octree, in order

to make use of spatial coherence. The merge algo-

rithm reads an octree node and merges all patch-

pairs whose priority is locally minimal. When no

further merges are possible in the internal memory

part, this region is extended around the octree-node

in internal memory that contains the lowest merge

priority. There will always be patches (border

patches), whose adjacent patches still reside in ex-

ternal memory and thus prevent the computation of a

merge priority. Patches adjacent to border patches

cannot be used for merging, because it is impossible

to determine whether their priorities are locally

minimal. Thus there will always remain patches with

low priorities in internal memory, which can be used

to extend the internal memory footprint until all re-

maining patches reside in internal memory.

This process continues until no further, locally

minimal merge operations are possible. When the

internal memory usage exceeds a given threshold,

parts of the internal memory are written back to the

octree. During the merge process, the indices of the

two merged patches and of their parent patch are

stored into an external heap, weighted with their

compactness measure (descending). When the com-

pactness value of one of the child patches is higher

than the one of the resulting patch, the highest com-

pactness measure is associated with the heap item.

This enables refining the resulting binary hierarchy

of patches by simply removing items from the heap.

After a number of items was removed from the heap,

the leaf patches and their binary subtree can be col-

lected from the heap. The leaf nodes of the subtrees

contain the associated triangles of the patch.

3.1.2 Straighten Patch Borders

The leaf patches, which were generated in the last

paragraph, have relatively rough borders. To im-

prove the synthesis of approximations, the borders

should be smoothed. Figure 2 shows a the difference

between the initial rough borders and the straight-

ened borders. It is visible that the general shape was

preserved in the smoothing process, while many

small corners were smoothed.

Figure 2: Straightened patch borders.

To straighten the borders of the patches, the path

length has to be shortened between two sequenced

patch corners. The shape of the patches is preserved

with the use of local shorten-operations only. Only

vertices in the direct neighborhood of the path (1-

neighborhood) can be used in the optimization. Due

to the large amount of data that has to be processed,

this process is serialized again.

The optimization heap is constructed from the

triangles of the surface. The triangles are first sorted

by their patch index with another heap. This enables

to collect the triangles per patch. Then each triangle

is brought to the optimization heap. The triangles are

weighted corresponding to the data associated with

the patch. If all adjacent patches have higher indices,

the patch index of the triangle is chosen. Otherwise

the lowest index of the adjacent patches is chosen.

This ensures that each triangle occurs only once in

the optimization heap. After the optimization heap is

initialized, all triangles with the same priority are

read from the heap into the internal memory. In in-

ternal memory the optimization for the available

borders between the patches can be computed, by

iteratively shortening the border path in the local

neighborhood. Only the 1-neighborhood (1 vertex

distance to the previous path) is considered during

the optimization. After that, the resulting triangles

are written back to external memory. If the triangle

is associated with a patch whose adjacent patches

have all higher indices than the current priority, this

triangle is written to the result heap and weighted

with its associated patch index. Otherwise the trian-

gle is brought back to the optimization heap,

weighted with the lowest index among the associ-

ated patch and its direct neighbors that is greater

than the current priority. This process is repeated

until all triangles are situated in the result heap.

OUT OF CORE CONSTRUCTION OF PATCH TREES

155

Figure 3: Example patches.

Figure 3 shows an example for this process. The

surface is divided into six patches and all patch bor-

ders have to be tested for optimizations. First the

optimization heap is initialized with all triangles of

the six patches. In this example

describes the set

of triangles that belongs to patch p and has the prior-

ity w. The initial heap now looks like this:

T ,

First the triangles with the priority 0 are read

from the heap. The borders between the patches 0

and its neighbors 1, 2, 3, 5 are tightened. After that,

all triangles of patch 0 are written to the result heap,

because all border segments have been processed.

All other triangles are written back to the optimiza-

tion heap, weighted with the next larger patch index

among the neighbor patches. This results in the fol-

lowing sequence:

T ,

Now all triangles with a priority of 1 are read

from the optimization heap. The border segments

between patch 1 and patches 2, 3 and 4 are

smoothed. The border between patch 1 and patch 0

has already been smoothed, when patch 0 was proc-

essed. After that, the triangles of patch 1 are brought

to the result heap while the other triangles are writ-

ten back to the optimization heap, weighted with the

next patch index in their neighborhood. This results

in the optimization heap:

T ,

The optimization continues, until all triangles are

brought to the result heap. Then all triangles can be

collected from the result heap, according to their

final patch index.

3.1.3 Create Patch Hierarchy

In this last step, the final patch tree is created from

the given leaf patches. This includes the creation of

new patch levels together with geometric simplifica-

tions of the surface. The geometry is simplified with

iterative half-edge collapse (Kobbelt, 1996) opera-

tions. The sequence of collapses is controlled by the

QEM (Garland, 1996).

The patch tree structure should completely fit

into the internal memory now. Thus, all further

merge operations are executed without access to

external memory. The triangle data of the patches

however, does not fit into the internal memory and

has to remain in external memory. Thus, the process

of surface simplification has to be optimized for

external memory as well.

Before the process starts, initial QEM matrices

are computed for each vertex. This can easily be

serialized with external heaps again. After that, the

new patch level is created by halving the number of

current patches. Now the number of triangles has to

be halved from the current patch level to the new

patch level. Therefore all triangles and vertices of

the current level are written to a temporary file, as-

sociated with their new patch index. Now the ge-

ometry data of each patch can be read as one block

from external memory.

The geometric simplification is similar to the

creation of the initial patches in the beginning. First,

an arbitrary patch is read from the external memory

to the internal memory. Then the vertices in internal

memory are classified into border, near-border and

inner vertices. The border vertices have the property

that at least one direct neighbor is not yet in the in-

ternal memory. The near-border vertices must have

at least one border vertex in their neighborhood,

while inner vertices have only other inner or near-

border vertices in their neighborhood. Thus, col-

lapse targets can be found for near-border and inner

vertices only, while locally minimal collapse opera-

tions can be found among inner vertices only.

After the patch geometry is read and classified,

all possible locally minimal collapse operations are

performed. For each collapse operation, the indices

of both collapsed vertices are brought to an external

heap (descending), weighted with their collapse er-

ror. If one of the collapsed vertices had a higher

QEM error, this error is used as heap priority. Then

the near-border vertex with the least QEM error is

chosen, in order to expand the region in the internal

memory around the associated patches (vertices can

be shared by multiple patches). The geometry of the

new patches is read from external memory and clas-

sified. This includes an update of some vertices,

which already reside in internal memory, because

their border/near-border status could have changed.

Again, all locally minimal collapse operations are

performed and the region in the internal memory is

expanded. This process is repeated, until no further

expansion is possible. Whenever the amount of used

internal memory exceeds a given threshold, the ge-

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

156

ometry of patches with the highest near-border

QEM errors, is moved back to external memory.

After the process has finished, all patches have

to be checked whether they contain inner vertices or

not. If inner vertices remained, the process has to be

started again with one of these patches. Such non-

processed inner vertices can occur under some cir-

cumstances, when a region is surrounded by com-

pletely processed patches and is then written to ex-

ternal memory.

After the simplification, we get a heap that con-

tains a sequence of collapse operations and thus the

simplification hierarchy. To extract the geometry for

the new patch tree level, the result vertices have to

be refined. This is done by removing the first items

from the heap, until the correct number of triangles

is reached. Now the geometry is adopted to the re-

fined vertices and stored according to the patches in

the new patch level.

The creation of new patch levels and the simpli-

fication of the geometry are repeated, until the num-

ber of patches reaches a given threshold. The result

is a patch tree, with a structure like the one in the

first figure. All leaf nodes are situated in the same

level and have a parent node in the next level, except

for the root node.

3.2 LoD Synthesis

Once the patch tree has been created, it can be used

to assemble approximations of the original mesh. To

measure the effect of an patch refinement in the ap-

proximation, object space errors have to be com-

puted. Therefore all child patches are recursively

projected to their parent patches. Now the average

squared distance of all vertices to their projection is

computed. The projection is computed by locking

the common vertices in both levels and by placing

the other vertices according to their locked

neighbors. The placement is determined with the

mean value coordinates (Floater, 2001). After the

vertices of the child patches have been projected to

their parent patch, the average squared distance to

their original position is computed. Furthermore, the

center and radius of a bounding sphere for each

patch is computed to enable view frustum culling.

For a view-dependent approximation a priority

queue (descending) is initialized with the root

patches. The object space error of each queued patch

is computed by dividing the average squared dis-

tance of the patch with the squared distance to the

viewer. Furthermore, a view frustum test is per-

formed for each patch, to determine whether it is

visible. Invisible patches are marked and assigned to

a view dependent error value of zero.

During the refinement, the first item is iteratively

read from the priority queue and used for refine-

ment. The refinement step is constrained to allow

only patch splits, if the parent patches of its neighbor

patches (in the same patch level) have already been

split. If not, these parent patches are split before the

current patch (forced split). This ensures a maximum

level difference of 1 between adjacent patches in the

final approximation.

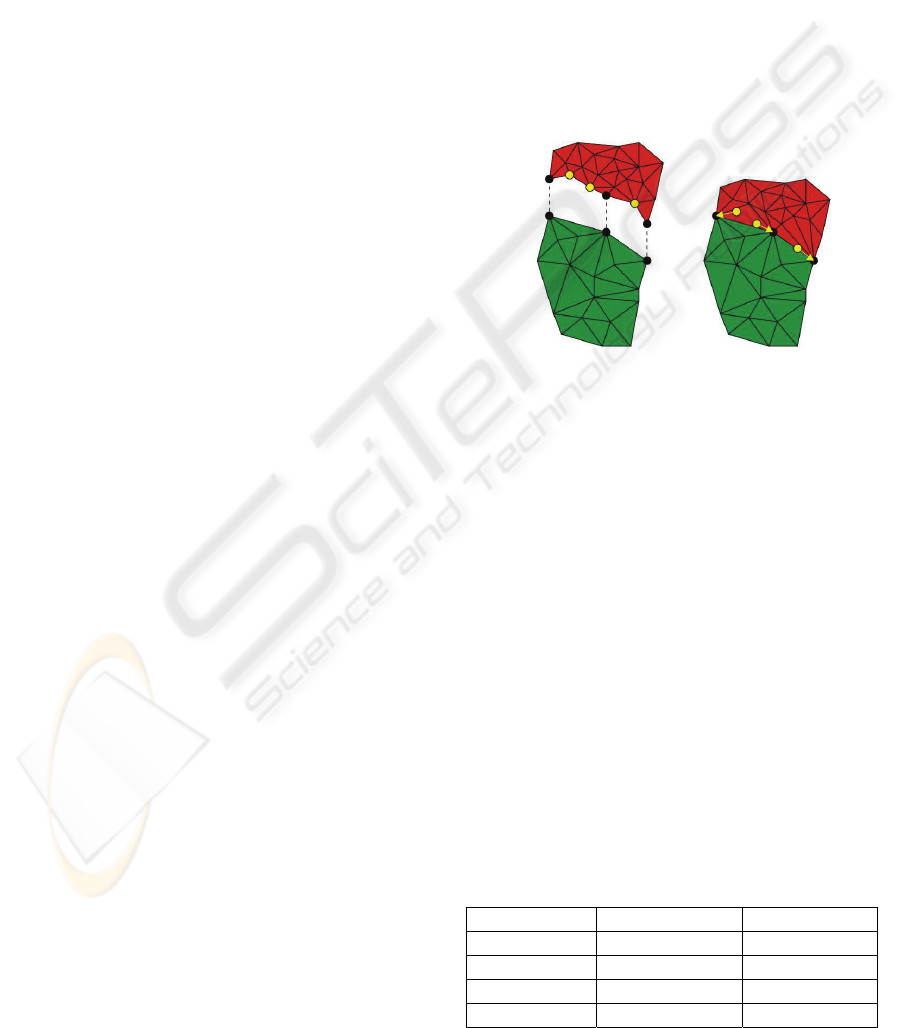
Before the approximation is sent to the GPU, all

transitions between patches of different levels have

to be created. Due to the constrained possible transi-

tions, all states of triangles in the transition area can

be computed in an offline process. Figure 4 shows

how a border segment of a higher level patch is

adopted to a lower level patch.

Figure 4: Patch transition.

The changes in the geometry due to the level

transition introduce new surface errors in the ap-

proximated surface, but these errors occur only at

borders to coarser detail-levels which have an higher

approximation error anyway.

The reference to all vertices in the high level

patch, which do not occur in the low level patch, are

moved to the nearest common vertex on the border

segment. Finally the geometry of all patches can be

sent to the GPU.

4 RESULTS

The patch tree construction process has been imple-

mented and tested with different meshes. Due to the

early prototype status of the software, only water-

tight meshes (no holes in the surface) can be proc-

essed for now. Table 1 lists four test meshes.

Table 1: Test meshes.

Name Triangles Vertices

Armadillo 345,944 172,974

Artificial 1 8,388,608 4,194,306

Artificial 2 33,554,432 16,777,218

Artificial 3 134,217,728 67,108,866

OUT OF CORE CONSTRUCTION OF PATCH TREES

157

Due to the lack of large watertight meshes the

last three meshes were computed with a fractal sub-

division method on a sphere surface. There are only

differences in the details structure. Figure 5 shows

the leaf patches of the first two meshes.

Figure 5: Leaf patches of first two test meshes.

The results of the patch tree construction process

can be read on table 2. Patch trees with average

patch sizes of 1,000 triangles have been built for all

test meshes.

Table 2: Patch tree results.

Name Leaf

Patches

Tighten

Borders

Final Hi-

erarchy

Armadillo 71 s 46 s 102 s

Artificial 1 3,495 s 2,145 s 4,833 s

Artificial 2 10,089 s 6,391 s 16,408 s

Artificial 3 45,228 s 29,810 s 71,547 s

The first two meshes have been tested on a 2

GHz Pentium 4 machine with 1 GB of RAM and a

SCSI hard disc. Due to its minor size, the “Arma-

dillo” mesh was processed very fast. Almost all ex-

ternal memory operations have been cached by the

operating system. The last two meshes have been

processed with an Athlon64 3800+ with 4 GB of

RAM and a SATA hard disc. The size of the usable

memory (except for the final patch hierarchy struc-

ture) was set to 150 MB. The results still show a

relatively long processing time for the large meshes.

However, basic simplification algorithms that do not

care about spatial coherence or serialization, would

spend even weeks to process such large data-sets.

Moreover there is enough room for further speedups.

Especially a less primitive version of the external

heap would be very helpful.

The resulting patch hierarchies can be used for

interactive exploration of the corresponding triangle

meshes. The low complexity of the patch trees re-

duces the CPU load and thus enable better usage of

the GPU bandwidth. Surely the data should be fur-

ther processed. First the sequence of patch-data in

external memory can be improved by grouping se-

mantically near parts of the tree together. Further-

more the amount of data for the patches can be re-

duced by striping. And if a number of vertices below

65,536 can be guaranteed for each patch, the indices

can be stored with 16 bits instead of 32.

5 CONCLUSIONS

In this paper an process queue has been presented

which automatically generates patch trees from large

triangle meshes. A two day processing time for a

128M triangle mesh is not bad but improvable.

REFERENCES

Cignoni, P., Ganovelli, F., Gobbetti, E., Marton, F.,

Ponchio, F., Scopino, R., 2003. Batched dynamic

adaptive meshes for high performance terrain visuali-

zation., Computer Graphics Forum

Cignoni, P., Ganovelli, F., Gobbetti, E., Marton, F., Pon-

chio, F., Scopino, R., 2004, Adaptive tetrapuzzles: ef-

ficient out-of-core construction and visualization of

gigantic multiresolution polygonal models. ACM

Trans. Graph.

Cignoni, P., Ganovelli, F., Gobbetti, E., Marton, F.,

Ponchio, F., Scopino, R., 2005, Batched Multi

Triangulation, Proceedings IEEE Visualization.

Duchaineau, M.A., Wolinsky, M., Sigeti, D.E., Miller,

M.C., Aldrich, C., Mineev-Weinstein, M.B., 1997,

ROAMing terrain: Real-time optimally adapting

meshes, Proceedings IEEE Visualization

Floater, M.S., 2003, Mean value coordinates, Computer

Aided Geometric Design

Garland, M., Heckbert, P.S., 1997, Surface Simplification

Using Quadric Error Metrics, SIGGRAPH ’97 Con-

ference Proceedings

Hoppe, H., 1997, View Dependent Refinement of Progres-

sive Meshes, Computer Graphics

Kobbelt, L., Campagna, S., Vorsatz, J., Seidel, H.-P.,

1998, Interactive multi-resolution modeling on arbi-

trary meshes, Proceedings of the 25th annual confer-

ence on Computer graphics and interactive techniques

Puppo, E., 1996, Variable Resolution terrain surfaces,

Proc. Of 8

Canadian Conference of Computational

Geometry

Sander, P.V., Snyder, J., Gortler, S.J., Hoppe, H., 2001,

Texture Mapping Progressive Meshes, Computer

Graphics Proceedings, ACM Press

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

158