
TRAFFIC SIGN CLASSIFICATION USING ERROR CORRECTING
TECHNIQUES
Sergio Escalera, Petia Radeva
Computer Vision Center, Dept. Computer Science, UAB, 08193 Bellaterra, Spain
Oriol Pujol
Dept. Matem
`
atica Aplicada i An
`
alisi, UB, Gran Via 585, 08007, Barcelona, Spain
Keywords:
Traffic Sign Classification, Error Correcting Output Codes, Ensemble of Dichotomies, Multiclass Classifica-
tion.
Abstract:
Traffic sign classification is a challenging problem in Computer Vision due to the high variability of sign
appearance in uncontrolled environments. Lack of visibility, illumination changes, and partial occlusions are
just a few problems. In this paper, we introduce a classification technique for traffic signs recognition by means
of Error Correcting Output Codes. Recently, new proposals of coding and decoding strategies for the Error
Correcting Output Codes framework have been shown to be very effective in front of multiclass problems.
We review the state-of-the-art ECOC strategies and combinations of problem-dependent coding designs and
decoding techniques. We apply these approaches to the Mobile Mapping problem. We detect the sign regions
by means of Adaboost. The Adaboost in an attentional cascade with the extended set of Haar-like features
estimated on the integral shows great performance at the detection step. Then, a spatial normalization using
the Hough transform and the fast radial symmetry is done. The model fitting improves the final classification
performance by normalizing the sign content. Finally, we classify a wide set of traffic signs types, obtaining
high success in adverse conditions.
1 INTRODUCTION
Traffic sign classification in uncontrolled environ-
ments is a hard task in Computer Vision due to the
high variability of symbol appearance caused by il-
lumination changes, lack of visibility, or occlusions.
In the last years, several approaches to deal with
the problem have been proposed. Usually, traffic
sign recognition strategies are divided into two main
groups: color-based and grey scale-based. Grey
scale-based approaches focus on object geometry,
whereas color-based techniques allow to prevent false
positives detection. Traffic sign recognition is stud-
ied for several purposes, like autonomous driving un-
der certain simplified conditions or for assisted driv-
ing (Handmann et al., 1998). We focus on the goal
of mobile mapping (Casacuberta et al., 2004), as a
technique used to compile cartographic information
from a mobile system. One of the main difficulties
that makes this problem hard is the great number of
classes and the high resemblance among signs in poor
resolution images. In order to deal with these hin-
drances, robust multiclass classifiers must be consid-
ered.
Error Correcting Output Codes were born as an
alternative for handling multiclass problems using bi-
nary classifiers (Dietterich and Bakiri, 1995). It is
well-known that ECOC, when applied to multiclass
learning problems, can improve the generalization
performance (Windeatt and Ghaderi, 2003)(Allwein
et al., 2002). One of the reasons for this improvement
is its property to decompose the original problem into
a set of complementary two-class problems -coded in
the ECOC matrix- that allows sharing of classifiers
across the original classes.
Recently, there has been a renewed interest in
the design of Error Correcting Output Codes. The
common pre-designed coding strategies (one-versus-
one and one-versus-all) have been improved with
problem-dependent designs (Pujol et al., 2006)(Es-
calera et al., 2006b). On the other hand, new stud-
ies on the decoding step (Escalera et al., 2006a) have
281
Escalera S., Radeva P. and Pujol O. (2007).
TRAFFIC SIGN CLASSIFICATION USING ERROR CORRECTING TECHNIQUES.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 281-285
Copyright
c
SciTePress

shown that the performance of the ECOC classifica-
tion can be improved considering carefully the decod-
ing strategy applied. The new approaches take into
account that when one use a third symbol (zero) in
the ECOC matrix, that means that a particular class
is not considered by a classifier. In those cases, the
behavior of the decoding strategies should be adapted
to the influence of the zero symbol (Escalera et al.,
2006a).
In this paper, we deal with the problem of traf-
fic sign classification. We use the information ob-
tained from a Mobile Mapping System (Casacuberta
et al., 2004) to analyze the road video sequences. We
use Adaboost with the Haar-like features estimated
over the integral image (Viola and Jones, 2002) to
detect regions with high probability of containing a
traffic sign. After applying a spatial normalization
and model fitting, we classify the candidate signs in
their different categories. We compare the recently
proposed coding and decoding strategies in the frame-
work of Error Correcting Output Codes, showing the
improvement of these last techniques when problem-
dependent ECOC designs are combined with proper
decoding strategies. The proposed ECOC designs ro-
bustly classify several types of signs with high vari-
ability.
The paper is organized as follows: section 2
overview the Error Correcting Output Codes and the
state-of-art on coding and decoding strategies. Sec-
tion 3 explains the system for traffic signs classifica-
tion. Section 4 shows experimental results, and sec-
tion 5 concludes the paper.
2 ERROR CORRECTING
OUTPUT CODES
The basis of the ECOC framework is to create a code-
word for each of the N
c
classes. Arranging the code-
words as rows of a matrix, we define a ”coding ma-
trix” M, where M ∈ {−1, 0,1}
N
c
×n
in the ternary case,
being n the code length. From the point of view of
learning, M is constructed by considering n binary
problems (dichotomies), each corresponding to a ma-
trix column. Joining classes in sets, each dichotomy
defines a partition of classes (coded by +1, -1, accord-
ing to their class set membership, or 0 if the class is
not considered by the dichotomy). In fig.1 we show an
example of a ternary matrix M. The matrix is coded
using 7 dichotomies {h
1
,..., h
7
} for a four multiclass
problem (c
1
, c
2
, c
3
, and c
4
). The white regions are
coded by 1 (considered as positive for its respective
dichotomy, h
i
), the dark regions by -1 (considered
as negative), and the grey regions correspond to the
zero symbol (not considered classes for the current
dichotomy). For example, the first classifier is trained
to discriminate c
2
versus c
1
,c
3
and c
4
, the second one
classifies c
3
versus c
1
, and so on. Applying the n
trained binary classifiers, a code is obtained for each
data point in the test set. This code is compared to the
base codewords of each class defined in the matrix M,
and the data point is assigned to the class with the
”closest” codeword (Allwein et al., 2002)(Windeatt
and Ghaderi, 2003). In the case of the figure, a new
test input x is evaluated by all the classifiers and the
systems assigns the label c
1
with minor Euclidean de-
coding distance d(x,y
i
) =
q
∑
n
j=1
(x
j
− y
i
j
)
2
, where y
is a class codeword, and n is the total number of bi-
nary classifiers.
Figure 1: ECOC design and input test classification.
3 TRAFFIC SIGN
CLASSIFICATION SYSTEM
We focus on the goal of mobile mapping to compile
cartographic information from a mobile system. In
particular, we use the video sequences obtained from
the Mobile Mapping System of (Casacuberta et al.,
2004). In this system, the position and orientation
of the different traffic signs are measured in move-
ment with the car video cameras. The system has a
stereo pair of calibrated cameras, which are synchro-
nized with a GPS/INS system. Therefore, the result of
the acquisition step is a set of stereo-pairs of images
with their position and orientation information.
The traffic sign recognition system used is divided
in three main steps: object detection, model fitting,
and classification. Each of these steps must be robust
enough to minimize the propagation of errors in the
system.
The detection process is based on the face detec-
tor presented by Viola and Jones in (Viola and Jones,
2002). In particular, we use the Discrete version
of Adaboost with decision stumps (Friedman et al.,
1998). The weak classifiers are trained using the at-
tentional cascade based on the extended set of Haar-
like features (that is, including the rotated ones) esti-
mated on the integral image (Viola and Jones, 2002).

Figure 2: Detected traffic signs.
As a result of the detection process, we obtain results
as in fig. 2.
Given an image where the Adaboost learning al-
gorithm detected a road sign, a region of interest
(ROI) that contains a sign is determined (circular or
triangular). However, since we have missing informa-
tion about sign scale and position, before the recog-
nition process we apply a spatial normalization to
improve final recognition. In particular, the Hough
transform (Morse, 2000) and fast radial symmetry
(Loy and Zelinsky, 2003) are applied in order to fit the
model since they offer great robustness against noise.
The fast radial symmetry is calculated over a set
of one or more ranges, depending on the scale of
the features one is trying to detect. The value of
the transform at a range indicates the contribution
to radial symmetry of the gradients at a distance n
away from each point. At each range n, we ex-
amine the gradient g at each point p, from which
a corresponding positively-affected pixel p
+ve
(p)
and negatively-affected pixel p
−ve
(p) are determined
and accumulated in the orientation projection im-
age O
n
: P
±ve
(p) = p ± round
g(p)
||g(p)||
n,O
n
(P
±ve
(p)) =
O
n
(P
±ve
(p)) + 1. Now, to locate the center of ra-
dial symmetry, we search for the position (x, y) of
maximal value in the accumulated orientations matrix
O
T
=
∑
n
i=1
O
n
. Locating that maximum we determine
the radius length. This procedure allows to obtain ro-
bust results for circular traffic signs fitting.
The Hough transform has been shown to allow the
detection of straight lines in a robust way. We apply
this procedure in order to look for the three represen-
tative lines of the triangular sign and calculate their in-
tersections to transform the image. Nevertheless, we
need to consider additional restrictions to obtain the
three representative border lines of a triangular traffic
sign. Each line has associated a position in relation to
the others. Once we have the three detected lines we
calculate their intersection. Given the parameters a
and b that define the equation y = a×x+ b for each of
the three lines, the intersection point (X,Y) for each
pair of lines is defined as follows:
X
t
= (b
i
2
− b
i
1
)/(a
i
1
− a
i
2
), Y
t
= a
i
1
X
t
+ b
i
1
| t,i ∈ [1,..., 3]
(1)
To assure that the lines are the expected ones, we com-
plement the procedure searching for a corner at a cir-
cular region at each intersection surroundings:
S = {(x
i
,y
i
) | ∃p < ((x−x
i
)
2
+(y− y
i
)
2
−r
2
)} | i ∈ [1, ...,3]
(2)
where S is the set of valid intersection points, and p
corresponds to a corner point to be located in a neigh-
borhood of the intersection point.
Once the sign model is fitted using the commented
methods, the next procedure is the spatial normal-
ization of the shape before classification. The steps
are: transform the image to make the recognition in-
variant to small affine deformations reescaling to the
signs database size (32×32 pixels), filter with Weick-
ert anisotropic filter, and mask the image to exclude
background at the classification step. To prevent the
effects of illumination changes, the histogram equal-
ization improves image contrast and obtains a uni-
form histogram.
From 10 analyzed DVD video sequences, we have
obtained the classes in fig. 3. The classes are divided
in three main groups: speed, circular, and triangu-
lar, with a total of 27 different classes to recognize.
The speed signs are treated as an special case due to
their similarity and difficulty to discriminate in ad-
verse conditions. The three attentional cascades (one
for each group) have been trained using a total of 1500
positive samples divided into the tree different groups.
(a) (b) (c)
Figure 3: (a) Speed classes. (b) Circular classes. (c) Trian-
gular classes.
Applying the three attentional cascades at Mobile
Mapping System video sequences, the detected and
normalized regions are classified, depending of the
type of the detected sign, using different classification
strategies combining the presented coding and coding
strategies of Error Correcting Output Codes.
4 RESULTS
Applying the attentional cascades over a test set of
15000 road frames obtained from the Mobile Map-
ping System, we have detected 1200 regions that con-
tain traffic signs. The detected regions are divided in
the three groups of fig. 3. After applying the model
fitting and the spatial normalization, all pixels are
treated as a 1024 feature vector. The strategies used
to validate the classification are Discrete Adaboost
with decission stumps, and linear SVM with the reg-
ularization parameter C set to 1. These two classi-
fiers generate the set of binary problems to embed
in the set of ECOC configurations: one-versus-one,
one-versus-all, dense-random, DECOC (Pujol et al.,
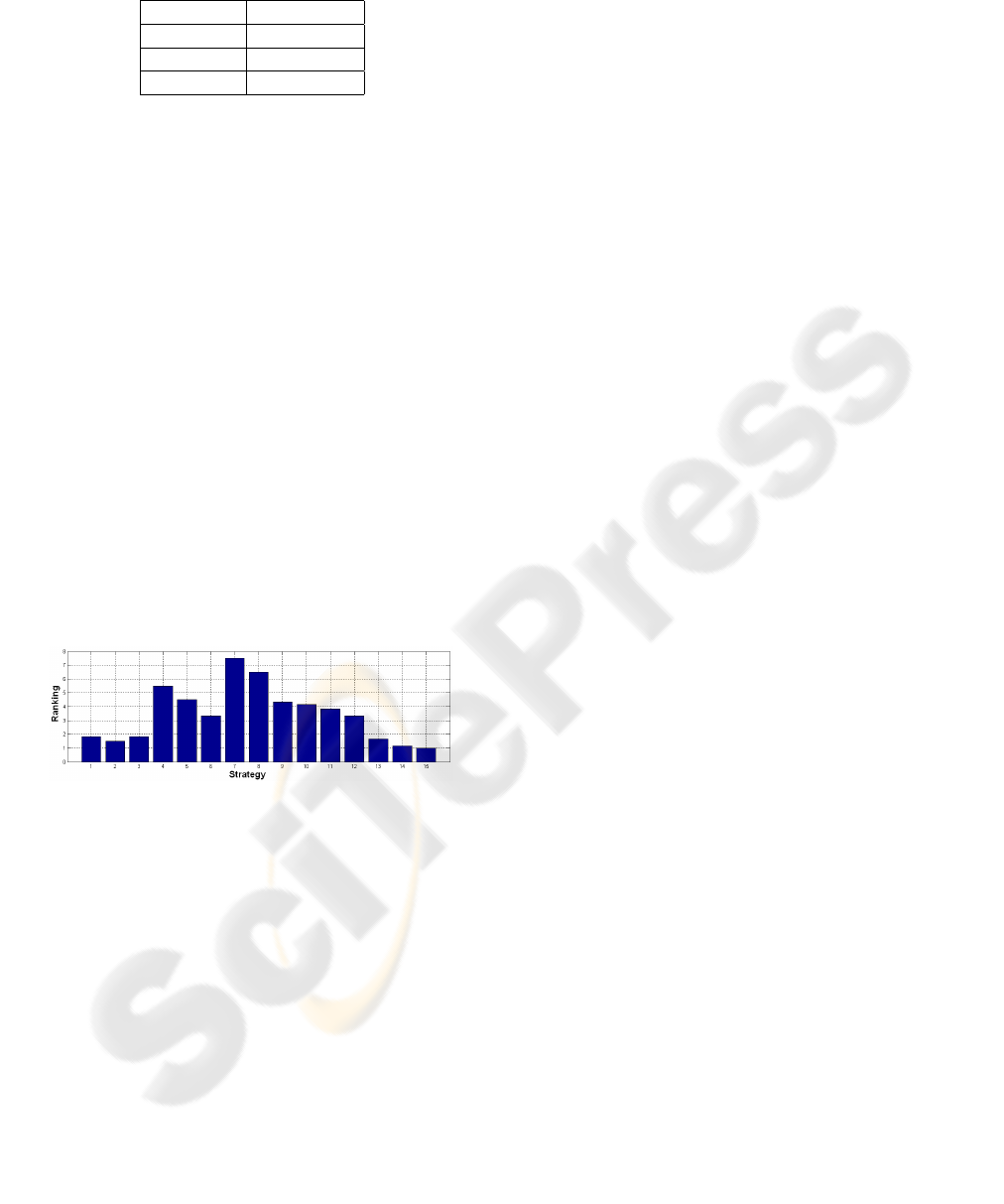
Table 1: Multiclass SVM results.
Problem Accuracy
Speed 76.96±0.84
Circular 97.02±0.77
Triangular 95.74±0.99
2006), and ECOC-ONE (Escalera et al., 2006b). Each
of the ECOC strategies are evaluated using different
decoding strategies: Euclidean distance, Laplacian
(Escalera et al., 2006a) and Pessimistic β-Density de-
coding (Escalera et al., 2006a). For the dense random
case, where we have selected n binary classifiers for a
fair comparison with one-versus-all and DECOC de-
signs in terms of a similar number of binary problems.
The classification tests are performed using stratified
ten-fold cross-validation with 95% of the confidence
interval.
We have generated three types of experiments,
each one for each of the three different traffic signs
groups. The mean rankings for each classification
strategy using the results of the three presented exper-
iments. The ranking is shown in fig. 4. One can ob-
serve that the best position is obtained by the ECOC-
ONE strategy, followed by one-versus-one, DECOC,
one-versus-all, and finally dense random strategy. It
is important to note that for each ECOC designs, the
Laplacian, and β-Density increase the classification
accuracy of Euclidean decoding for all the cases.
Figure 4: Ranking position for each classification strat-
egy. From left to right: (1)-one-versus-one Euclidean, (2)-
one-versus-one Laplacian, (3)-one-versus-one β-Density,
(4)-one-versus-all Euclidean, (5)-one-versus-all Laplacian,
(6)-one-versus-all β-Density, (7)-dense random Euclidean,
(8)-dense random Laplacian, (9)-dense random β-Density,
(10)-decoc Euclidean, (11)-decoc Laplacian, (12)-decoc
β-Density, (13)-ecoc-one Euclidean, (14)-ecoc-one Lapla-
cian, (15)-ecoc-one β-Density.
To show the robustness of the presented classifica-
tion framework, we compare the results obtained with
the ECOC methods with a built-in multiclass SVM.
The results are shown in table 1. One can observe
that the linear multiclass SVM obtains inferior results
to the ones obtained by one-versus-one and ECOC-
ONE strategies.
5 CONCLUSIONS
In this paper, we presented a classification scheme
that obtains a very high performance for the prob-
lem of traffic sign classification. The system has three
main stages: traffic sign detection, model fitting and
spatial normalization, and sign categorization. The
multiclass classification techniques are evaluated on
real video sequences obtained from a Mobile Map-
ping System. We compared the state-of-the-art and
recently proposed designs for Error Correcting Out-
put Codes, and we combined them with robust de-
coding strategies, showing high robustness and bet-
ter performance than traditional ECOC designs and
the state-of-the-art multiclassifiers. In particular, the
Laplacian and β-Density decoding strategies when
applied to the coding designs improve the system per-
formance. The presented traffic sign recognition sys-
tem obtains robust classification results in front of
high variability of the objects appearance.
ACKNOWLEDGEMENTS
This work was supported in part by the projects,
FIS-G03/1085, FIS-PI031488, MI-1509/2005, and
TIN2006-15308-C02-01.
REFERENCES
Allwein, E., Schapire, R., and Singer, Y. (2002). Reducing
multiclass to binary: A unifying approach for margin
classifiers. In Journal of Machine Learning Research,
volume 1, pages 113–141.
Casacuberta, J., Miranda, J., Pla, M., Sanchez, S., A.Serra,
and J.Talaya (2004). On the accuracy and performance
of the geomobil system. In International Society for
Photogrammetry and Remote Sensing.
Dietterich, T. and Bakiri, G. (1995). Solving multiclass
learning problems via error-correcting output codes.
In Journal of Artificial Intelligence Research, vol-
ume 2, pages 263–286.
Escalera, S., Pujol, O., and Radeva, P. (2006a). Decoding
of ternary error correcting output codes. In CIARP,
Lecture notes in Computer Science.
Escalera, S., Pujol, O., and Radeva, P. (2006b). Ecoc-one: A
novel coding and decoding strategy. In International
Conference on Pattern Recognition.
Friedman, J., Hastie, T., , and Tibshirani, R. (1998). Addi-
tive logistic regression: a statistical view of boosting.
In Technical Report.
Handmann, U., Kalinke, T., Tzomakas, C., Werner, M., and
von Seelen, W. (1998). An image processing system
for driver assistance. In IEEE International Conf. on
Intelligent Vehicles, pages 481–486.

Loy, G. and Zelinsky, A. (2003). Fast radial symmetry
for detecting points of interest. In IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
volume 25.
Morse, B. (2000). Segmentation (edge based, hough trans-
form). In Technical report.
Pujol, O., Radeva, P., and Vitri
`
a, J. (2006). Discriminant
ecoc: a heuristic method for application dependent de-
sign of error correcting output codes. In T. Pattern
Analysis and Machine Intelligence, volume 28, pages
1007–1012.
Viola, P. and Jones, M. (2002). Robust real-time object de-
tection. In International Journal of Computer Vision.
Windeatt, T. and Ghaderi, R. (2003). Coding and decod-
ing for multiclass learning problems. In Information
Fusion, volume 1, pages 11–21.
