
FACE TRACKING USING CANONICAL CORRELATION ANALYSIS
Jos
´
e Alonso Yb
´
a
˜
nez Zepeda
1
, Franck Davoine
2
and Maurice Charbit
1
1
Ecole Nationale Sup
´
erieure des T
´
el
´
ecommunications, Rue Barrault, Paris, France
2
Compiegne University of Technology, Heudiasyc lab., CNRS, Compi
`
egne, France
Keywords:
Canonical Correlation Analysis (CCA), Kernel Canonical Correlation Analysis (KCCA), Head Tracking.
Abstract:
This paper presents an approach that incorporates canonical correlation analysis for monocular 3D face track-
ing as a rigid object. It also provides the comparison between the linear and the non linear version (kernel) of
the CCA. The 3D pose of the face is estimated from observed raw brightness shape-free 2D image patches. A
parameterized geometric face model is adopted to crop out and to normalize the shape of patches of interest
from video frames. Starting from a face model fitted to an observed human face, the relation between a set
of perturbed pose parameters of the face model and the associated image patches is learned using CCA or
KCCA. This knowledge is then used to estimate the correction to be added to the pose of the face from an
observed patch in the current frame. Experimental results on tracking faces in long video sequences show the
effectiveness of the two proposed methods.
1 INTRODUCTION
Nowadays video object tracking presents a challeng-
ing problem for video applications such as face-based
biometric person authentication, human computer
interaction, video games, teleconferencing, surveil-
lance, etc. To deal with this problem, vision re-
search groups have proposed several approaches that
can be classified in two main groups: model-based
and learning-based approaches. In the first cate-
gory, tracking algorithms rely on a parametric model
of the object to be tracked. In the second cate-
gory, algorithms assume the availability of a train-
ing set of object examples, and use pattern recog-
nition/classification techniques. When working with
video images, we can obtain different features, such
as edges, interest points, grey level intensities or color
histograms, etc. The choice of these features will
depend on the tracked object’s characteristics. The
tracker is traditionally composed of two components:
a representation component to cope with changes in
the target appearance, (caused by a variation in illumi-
nation, an occlusion, a change in orientation or scale,
a facial expression, etc.), and a filtering component
(it adds temporal continuity constraints across frames
and deals with dynamics of the tracked object).
In this paper, we propose a deterministic approach
based on Canonical Correlation Analysis (CCA).
CCA has already been considered for the task of es-
timating an object’s pose from rawbrightness still im-
ages, for example in (Melzer et al., 2003).In our case,
using the work realized in (Davoine and Dornaika,
2005; La Cascia et al., 2000),we combine CCA with
a 3D generic face model to track people’s 3D head
pose as a rigid object. This document is structured
as follows: Section 2 introduces the 3D face model
and how we use it to compute shape-free 2D image
patches. Then, in section 3 we give a description of
Canonical Correlation Analysis (CCA) algorithm in
the linear and non linear form. After that, we present
how we link these concepts to track a face in a video
sequence. Section 4 presents the experimental results
obtained from long video sequences. Finally we give
our conclusions in section 5.
2 FACE REPRESENTATION
The use of a 3D geometric generic model for track-
ing purpose has been widely explored in the computer
396
Alonso Ybáñez Zepeda J., Davoine F. and Charbit M. (2007).
FACE TRACKING USING CANONICAL CORRELATION ANALYSIS.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 396-402
Copyright
c
SciTePress

vision community. It allows to acquire the 3D face
characteristics of a given person and the correspond-
ing texture map to this person’s face. In this section
we present the 3D geometric model used and the way
we employed it to obtain a normalized raw brightness
facial patch.
2.1 3d Geometric Model
In our work, we use the
Candide-3
wireframe model,
proposed by (Ahlberg, 2001). It consists of a group
of n 3D interconnected vertices to describe a face by
means of a small number of triangles, enough to reach
an acceptable realism to represent a face both stati-
cally and dynamically by means of shape and anima-
tion units.
The 3n-vector c consists of the concatenation of
all the vertices, and can be written in terms of the
modifications that it can be subject to, as:
c = c
s
+ Aτ
τ
τ
a
(1)
where Aτ
τ
τ
a
stands for the dynamic part of the model,
being the columns of A the Animation Units and τ
τ
τ
a
the animation control vector. The vector c
s
=
c+ Sτ
τ
τ
s
corresponds to the static characteristics of a given per-
son (like the nose size, eye separation distance, etc.),
being
c the standard shape of the Candide model, the
columns of S are the Shape Units, and τ
τ
τ
s
is the shape
control vector (Ahlberg, 2001). The vectors τ
τ
τ
s
and τ
τ
τ
a
are initialized manually, by fitting the Candide shape
over the face in the first video frame. Figure 1 shows
the initialization as well as the 3D model with the tex-
ture warped on it in a frontal view and in three ro-
tated views. These views are useful to adjust the z-
component parameters of τ
τ
τ
s
and τ
τ
τ
a
during the model
initialization step. The vector τ
τ
τ
a
is supposed to be
constant: the face is seen as a rigid object during the
tracking process, with a fixed expression.
Figure 1: Candide. model placed over the target face in the
first video frame with frontal and three rotated views.
When placing the Candide model over the first
frame, we obtain the 3D pose parameters, that we put
in our state vector b, given by:
b = [θ
x
,θ
y
,θ
z
,t
x
,t
y
,t
z
] (2)
where the θ elements stand for the rotations and the
t elements stand for the translations that we want to
track. When we place the model over the first video
frame, we crop the texture that lies under it and warp
it to the 3D model surface for tracking purposes, as
described below.
2.2 Normalization of the Raw
Brightness Facial Patch
When tracking a moving face in a 3D environment,
we face the problem that its size and geometry are not
constant, making difficult the direct construction of
a facial appearance model. To cope with this prob-
lem, we build a stabilized 2D shape free image patch
(a texture map) to code the facial appearance of the
person facing the camera. This patch is obtained by
warping the rawbrightness image vector lying under
the initialized model c(b) at time t = 0 into a fixed
size (in our case d = 96× 72 pixels) 2D projection of
the reference Candide model without any expression,
i.e. τ
τ
τ
a
set to zero. The patch is finally augmented
with the two semi-profile views of the face, as shown
in Figure 2.
We can express this mathematically as it was done
in (Davoine and Dornaika, 2005) as a transforma-
tion
W of the texture observed at each frame Y
t
.
For a given state vector b, the observation vector
x
t
= W (b, Y
t
) consists of the columns of the stabi-
lized face image stacked one after the other and nor-
malized such that
q
∑
d
i=1
x
2
i
= 1.
10 20 30 40 50 60 70 80 90
10
20
30
40
50
60
70
Figure 2: Expression-free patch, used to represent the target
face.
3 TRACKING PROPOSITION
The main idea of our algorithm is to estimate the rela-
tion that exists between the variation of the state vec-
tor and the difference between the current observation
vector and the reference vector. To perform this, we
consider two approaches to learn a relation between

a set of perturbed state parameters and the associated
image patches. One is based on Canonical Correla-
tion Analysis, and the other one on kernel CCA to
search for the relationships in the higher dimensional
space. In this section we will briefly introduce CCA
and KCCA, as well as the way we use them to find
the model that establishes the relation we are looking
for.
3.1 Canonical Correlation Analysis
Canonical correlation analysis is a way of identifying
and quantifying the linear relationship between two
data sets of random variables. CCA can be seen as the
problem of finding basis vectors for two sets of vari-
ables, one for Q
1
and the other for Q
2
, such that the
correlation between the projections of the variables
onto these basis vectors are mutually maximized.
Let A
1
and A
2
be the centered data sets corre-
sponding to the Q
1
data matrix of dimension m × n
and Q
2
the data matrix of dimension m × p respec-
tively. The maximum number of correlations that can
be found is equal to the minimum of the data sets’
column dimension min(n, p). If we map our data to
the directions w
1
and w
2
we obtain, for each pair of
directions, two new vectors defined as:
z
1
= A
1
w
1
and z
2
= A
2
w
2
(3)
These vectors are called the scores (Borga et al.,
1997; Dehon et al., 2000; Weenink, 2003), and we
are interested in finding the correlation between them,
which is defined as:
ρ =
z
T
2
z
1
q
z
T
2
z
2
q
z
T
1
z
1
(4)
Our problem is to find the vectors w
1
and w
2
that
maximize (4) subject to the constraints z
T
1
z
1
= 1 and
z
T
2
z
2
= 1. In order to do that, we formulate our prob-
lem in a Lagrangian form.
As we have the data matrices A
1
and A
2
we can
use the method proposed in (Weenink, 2003), to re-
duce the number of matrix operations, where they per-
form the singular value decomposition of the data ma-
trices A
1
= U
1
D
1
V
T
1
and A
2
= U
2
D
2
V
T
2
, then they
introduce the singular value decomposition: U
T
1
U
2
=
UDV
T
, to finally get:
W
1
= V
1
D
−1
1
U and W
2
= V
2
D
−1
2
V (5)
where we denote W
1
and W
2
as the matrices contain-
ing respectively the canonical correlation basis vec-
tors w
1
and w
2
.
The main advantage of this procedure is that it
avoids the estimation of the covariance matrices and
the calculation of the corresponding inverses, and in-
stead, we need to perform three singular value decom-
positions, which are numerically more robust.
3.2 Tracking Implementation Using the
Cca
Once we have shown the CCA, we can proceed to
describe our tracking algorithm. It consists of three
steps: Initialization, Training process, and Tracking
process.
Initialization. During the initialization we place the
Candide model over the first video frame Y
0
, and ad-
just it to the person’s characteristics as previously de-
scribed, obtaining the state vector b
0
, and the refer-
ence vector at time t = 0 as:
x
(ref )
0
=
W (b
0
,Y
0
) (6)
Training process. It consists of obtaining a linear
model containing the relation between the variation in
the state vector ∆b
t
and the vector resulting from the
difference of the observation vector and the reference
vector x
t
− x
(ref )
t
.
To obtain this relationship, we need to define the
data matrices A
1
and A
2
. The matrix A
1
contains the
difference between the m training observation vectors
x
Training
=
W (b
Training
,Y
0
) and the reference x
(ref )
0
,
and the matrix A
2
contains the corresponding vari-
ation in the state vector obtained from the relation
∆b
Training
= b
Training
−b
0
. The m training points were
chosen empirically from a non-regular grid around the
vector state obtained at initialization. From these ma-
trices we can obtain the canonical correlation basis
vectors as described before. Once we have obtained
this basis, the general solution consist in doing a lin-
ear regression between z
1
and z
2
. However, if we de-
velop 4 for each pair of directions with the assump-
tions made above, we arrive at kA
1
w
1
− A
2
w
2
k
2
=
2(1− ρ) similarly as in (Hardoon et al., 2004). In our
case, we have ρ ≈ 1 (from experimental data), so, we
have the following relation:
A
1
w
1
= A
2
w
2
(7)
that simplifies the obtention of our model by avoiding
the linear regression needed when ρ 6= 1.
We suppose that the learned relations from the ma-
trices A
1
and A
2
are valid for the current ∆b
t
and
(x
t
− x
(ref )
t
) in (7), then we can then write:

∆b
t
w
2
= (x
t
− x
(ref )
t
)w
1
(8)
If we write the result for all the pair of directions in
a matrix form, we can replace equations (5) in the last
equation, and after some mathematical manipulation,
we arrive at:
∆b
t
= (x
t
− x
(ref )
t
)G (9)
where the G matrix, that encodes the linear model
used by our tracker, is given by:
G = V
1
D
−1
1
UV
T
D
2
V
T
2
(10)
It is important to notice that the matrix G is only
valid for a certain rotation interval and it is very de-
pendent on the training points used and on the initial-
ization of the Candide model.
Tracking process. The tracking process estimates
the state vector variation ∆b
t
from the difference be-
tween the current observation vector and the reference
vector by means of the G matrix built during the train-
ing process. To perform this estimation, we obtain the
current observation vector, which depends on the cur-
rent video frame Y
t
and the state vector at the preced-
ing instant b
t−1
as:
x
t
=
W (b
t−1
,Y
t
) (11)
and then, we obtain the difference between the obser-
vation vector and the the reference vector x
(ref )
t
. Then
we use this difference vector and the G matrix to up-
date the state vector as:
ˆ
b
t
= b
t−1
+ (x
t
− x
(ref )
t
)G (12)
With
ˆ
b
t
, we get a new observation vector
ˆ
x
t
=
W (
ˆ
b
t
,Y
t
) and we compare it with the reference x
(ref )
t
to compute the error measure:
e(b
t
) =
d
∑
i=1
ˆx
i,t
− x
(ref )
i,t
σ
(ref )
i,t
!
2
(13)
where σ
2
t
is the variance of the reference vector. If
e(b
t
) is bigger than a certain threshold, we use the
state vector estimated
ˆ
b
t
in (12) and obtain again an
error measure. We iterate a fixed number of times (5,
in practice). Once the iterations are done, and in order
to increase the robustness of the tracker to weak illu-
mination changes, we proceed to update the reference
vector and its variance according to:
x
(ref )
t+1
= αx
(ref )
t
+ (1− α)
ˆ
x
t
(14)
σ
2
t+1
= ασ
2
t
+ (1− α)(
ˆ
x
t
− x
(ref )
t
)
2
(15)
being α = 0.99 obtained empirically.
This approach is useful when we work with data
that has a linear behavior. In our case this linear ap-
proach showed a good performance, but for compari-
son reason, we studied also the use of the kernel CCA,
to find out if an approach that can cope with non linear
relations, can outperform the linear approach previ-
ously described. In the following part, we will present
the Kernel Canonical Correlation Analysis and the al-
gorithm used for tracking purposes.
3.3 Kernel Canonical Correlation
Analysis
The main idea behind kernel methods is that we can
still apply a linear method to analyse a given data set,
but first we need to map this data into a high dimen-
sional feature space. Thus, using kernel-functions we
can formulate our problem as a non-linear version of
the original one with the advantage that the complex-
ity of the transformed problem is not linked to the
feature space dimension, but to the training data set
dimension, which means that we can use kernel trans-
formations to feature spaces of high dimensionality.
If we define A
1
and A
2
as the centred data sets
of dimension m × n and of dimension m × p respec-
tively, we can apply the CCA to the vectors φ(A
1
) =
(φ(a
(1)
1
)...φ(a
(1)
m
)) and θ(A
2
) = (θ(a
(2)
1
)...θ(a
(2)
m
)),
according to the kernel trick (see (Melzer et al.,
2003)), which are two non linear mappings.
Then we define the kernel matrices K,L by K
ij
=
φ(a
(1)
i
)φ(a
(1)
j
)
T
and L
ij
= θ(a
(2)
i
)θ(a
(2)
j
)
T
, with f
φ
and
g
θ
which can be seen as the coefficients of the linear
expansion of the principal vectors w
φ
and w
θ
in terms
of the transformed data, i.e., w
φ
= φ(A
1
)
T
f
φ
and w
θ
=
θ(A
2
)
T
g
θ
.
We can then define as for the CCA the correlation
between the transformed data as:
ρ =
g
T
θ
L
T
Kf
φ
q
g
T
θ
L
2
g
θ
q
f
T
φ
K
2
f
φ
(16)
which we maximize in the same way as for the CCA.
The problem that arises from KCCA is that we
work with a finite number of points in a high dimen-
sional feature space, which can lead us to useless re-
sults. To force useful solutions we introduce a pe-
nalizing factor in the norms of the associated weights
which leads us to the eigenvalue equations (for more
details see (Hardoon et al., 2004)):
(K+ κI)
−1
L(L+ κI)
−1
Kf
φ
= ρ
2
f
φ
(17)
(L+ κI)
−1
K(K+ κI)
−1
Lg
θ
= ρ
2
g
θ
(18)
We can then obtain the vectors f
φ
and g
θ
as the
eigenvectors of this equations.
3.4 Algorithm Implementation Using
the Kcca
As for the CCA, we can divide the algorithm in three
parts, the initialization being exactly the same as in
the case of the CCA. For the training process, we need
to obtain vectors f
φ
and g
θ
as described in the last
section, using the same data matrices as the ones de-
scribed for the CCA approach. It is important to point
out that in the case of the variation vectors, we did not
use any kernel. Once this is done, the starting point
for the tracking is equation (7) that can be developed
according to the KCCA as:
Kf
φ
≈ A
2
A
T
2
g
θ
(19)
If we develop as above, we can assume that the
tracking data satisfies also this equation and after
some mathematical manipulation we arrive at:
∆b
t
= K
t
f
φ
(A
T
2
g
θ
)
−1
(20)
Here we can see that the K
t
corresponds to the
kernel matrix at time t obtained between the training
vectors x
(i)
−1
=
W (b
(i)
−1
,Y
0
), i = 1...m and the actual
patch x
t
=
W (b
t−1
,Y
t
). However, for the algorithm
implementation, we compute a linear regression be-
tween the result of the product of the matrix kernel
Kf
φ
and the variation vector Q
2
, so that we have the
actualization equation:
∆b
t
= K
t
f
φ
G (21)
being the matrix G obtained from the training kernel
matrix K. We use in our case the Gaussian RBF ker-
nel function:
K(x
i
,x
j
) = exp(−
kx
i
− x
j
k
2
2σ
2
) (22)
In our experiments, the two parameters σ and κ
are set respectively to 0.009 and 0.003. They were
obtained empirically from simulations using training
sequences, and based on the method used in (Melzer
et al., 2003) to estimate a starting point.
4 RESULTS
In order to evaluate our proposals, we implemented
our algorithm on a PC with a 3.0 GHz Intel Pen-
tium IV processor and a NVIDIA Quadro NVS 285
graphics card. The non optimized implementation
uses OpenGL for the texture mapping and OpenCV
for the video capture. We have used the video se-
quences used by (La Cascia et al., 2000)
1
, the an-
notated talking face video
2
, as well as some video
sequences made with a Winnov analog video camera
XC77B/320.
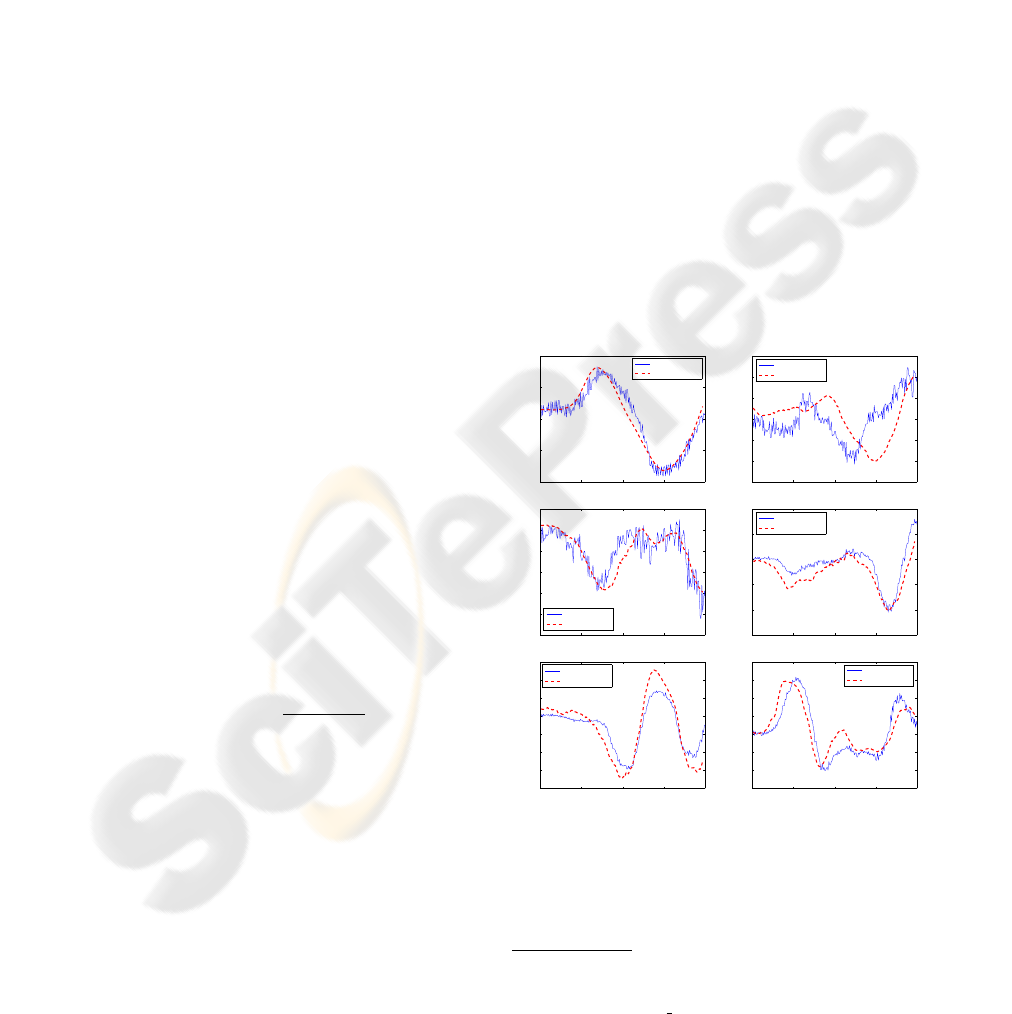
Figure 3 shows the results obtained from the CCA
algorithm. It depicts the state vector estimated com-
pared to the ground truth provided by (La Cascia
et al., 2000). We see that the performance of our
tracker is close to the ground truth. However, the co-
ordinate system used by our system is not the same as
that of the data given, specially for the translationand
hence compare them we had normalized both data.
There is also a issue with the rotation axes, which are
not located at the same point in our system (where
the three axes cross close to the nose, due to the Can-
dide model’s specification), and in the ground truth
data provided (where the 3D magnetic tracker was at-
tached on the subjects head). This discrepancy caused
principally the difference in the translation parame-
ters, because what in one system represents a rotation,
in the other system represents a rotation and a trans-
lation.
0 50 100 150 200
−2
−1
0
1
2
frame
X position normalized
Ground Truth
Estimation
0 50 100 150 200
−3
−2
−1
0
1
2
3
frame
Y position normalized
Ground Truth
Estimation
0 50 100 150 200
−4
−3
−2
−1
0
1
2
frame
Scale normalized
Ground Truth
Estimation
0 50 100 150 200
−30
−20
−10
0
10
20
frame
Rx in degrees
Ground Truth
Estimation
0 50 100 150 200
−40
−30
−20
−10
0
10
20
30
frame
Ry in degrees
Ground Truth
Estimation
0 50 100 150 200
−15
−10
−5
0
5
10
15
20
frame
Rz in degrees
Ground Truth
Estimation
Figure 3: Ground truth compared with the CCA algorithm’s
results.
Figure 4 depicts some video frames taken from
two tracked videos from (La Cascia et al., 2000) and
1
http : //www.cs.bu.edu/groups/ivc/HeadTracking/
2
http : //www− prima.inrialpes. fr/FGnet/data/01−
TalkingFace/talking
face.html

a webcam video. The CCA and the KCCA algorithm
performance did not present any problem when track-
ing the head in these video sequences, especially be-
cause there are not facial gesture involved. In the case
of the webcam video, we succeeded in tracking cor-
rectly rotations in the y plane going as far as ±35
◦
.
However, when trying to go further, the algorithm
could not estimate the correct variation of the angle
and got lost.
Another test has been performed using a part of
the talking face video. This video presents slight head
pose changes compared with the previous employed
videos, but it presents more significant movements
due to facial gesture. This video shows a person en-
gaged in conversation in front of a camera. It comes
with ground truth data that consist of characteristic
face points annotated semi-automatically. From the
68 annotated points, we chose the 52 points that were
closer to the corresponding Candide model’s points.
Because these points were not exactly the same as the
ones given in the ground truth database, there existed
an initial distance between the points. In order to mea-
sure the behavior of our algorithm, we calculated the
standard deviation of this distance, as shown in Figure
5. We can see that the points that presented the higher
variance were those in the head’s contour.
In Figure 6 we can see the result of tracking the
talking face over 1720 frames. The importance of this
figure is that we can see the evolution of the error dur-
ing the video. We have seen that the peaks appearing
in this figure represent the moments when there was
a facial gesture or a important rotation. However, as
seen in the frames displayed, we can cosider that these
peaks does not represent a significant error between
the state vector estimated and the real head pose.
The time required per frame processing depends
on the video size, as can be seen in the table 1. In that
table we show also the comparison between the CCA
and the KCCA implementation.
Table 1: Comparation of time per frame.
Video’s size [pixels] time per frame [ms]
CCA 640× 480 147.6
CCA 720× 576 179.5
KCCA 320× 240 2486.7
5 CONCLUSIONS
We have seen that the pose tracking is well performed
with the two trackers implemented. They managed to
follow the head movements in long video sequences
of more than 1700 frames. The main advantage of this
algorithm is that it is simple and proved to be robust
to facial gesture. However, we observed from simu-
lations that the effectiveness of this kind of tracker is
dependant on the mask initialization, i.e., the 3D mask
must be correctly initialized, in pose and in facial fea-
tures at the first frame, otherwise, the tracker can get
lost because the model affects directly the texture ex-
traction and consequently the state vector predictor.
The results obtained by means of the CCA and the
KCCA did not present a significant difference. How-
ever, if we consider the computation time required for
the KCCA algorithm, which was 10 times slower than
the CCA algorithm, we can conclude that for the type
of data we use, it is better to use the linear approach.
In our future work we will add the gesture track-
ing, based on the CCA approach, principally for
tracking the mouth and eyebrows, and based on the
work of (La Cascia et al., 2000), we will include a
robust measure to the tracking algorithm.
REFERENCES
Ahlberg, J. (2001). Candide-3 – an updated parameterized
face. Technical Report LiTH-ISY-R-2326, Linkoping
University, Sweden.
Borga, M., Landelius, T., and Knutsson, H. (1997). A uni-
fied approach to PCA, PLS, MLR and CCA. Report
LiTH-ISY-R-1992, ISY, SE-581 83 Link
¨
oping, Swe-
den.
Davoine, F. and Dornaika, F. (2005). Real-Time Vision for
Human Computer Interaction, chapter Head and Fa-
cial Animation Tracking using Appearance-Adaptive
Models and Particle Filters. Springer Verlag.
Dehon, C., Filzmoser, P., and Croux, C. (2000). Robust
methods for canonical correlation analysis. In Kiers,
H., Rasson, J., Groenen, P., and Schrader, M., editors,
Data Analysis, Classification, and Related Methods,
pages 321–326. Springer-Verlag.
Hardoon, D., Szedmak, S., and Shawe-Taylor, J. (2004).
Canonical correlation analysis; an overview with ap-
plication to learning methods. Neural Computation,
16:2639–2664.
La Cascia, M., Sclaroff, S., and Athitsos, V. (2000). Fast,
reliable head tracking under varying illumination: an
approach based on registration of texture-mapped 3D
models. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 22(2):322–336.
Melzer, T., Reiter, M., and Bischof., H. (2003). Appearance
models based on kernel canonical correlation analysis.
Pattern Recognition, 36(9):1961–1973.
Weenink, D. (2003). Canonical correlation analysis. In
Proceedings of the Institute of Phonetic Sciences of
the University of Amsterdam, Netherlands, volume 25,
pages 81–99.
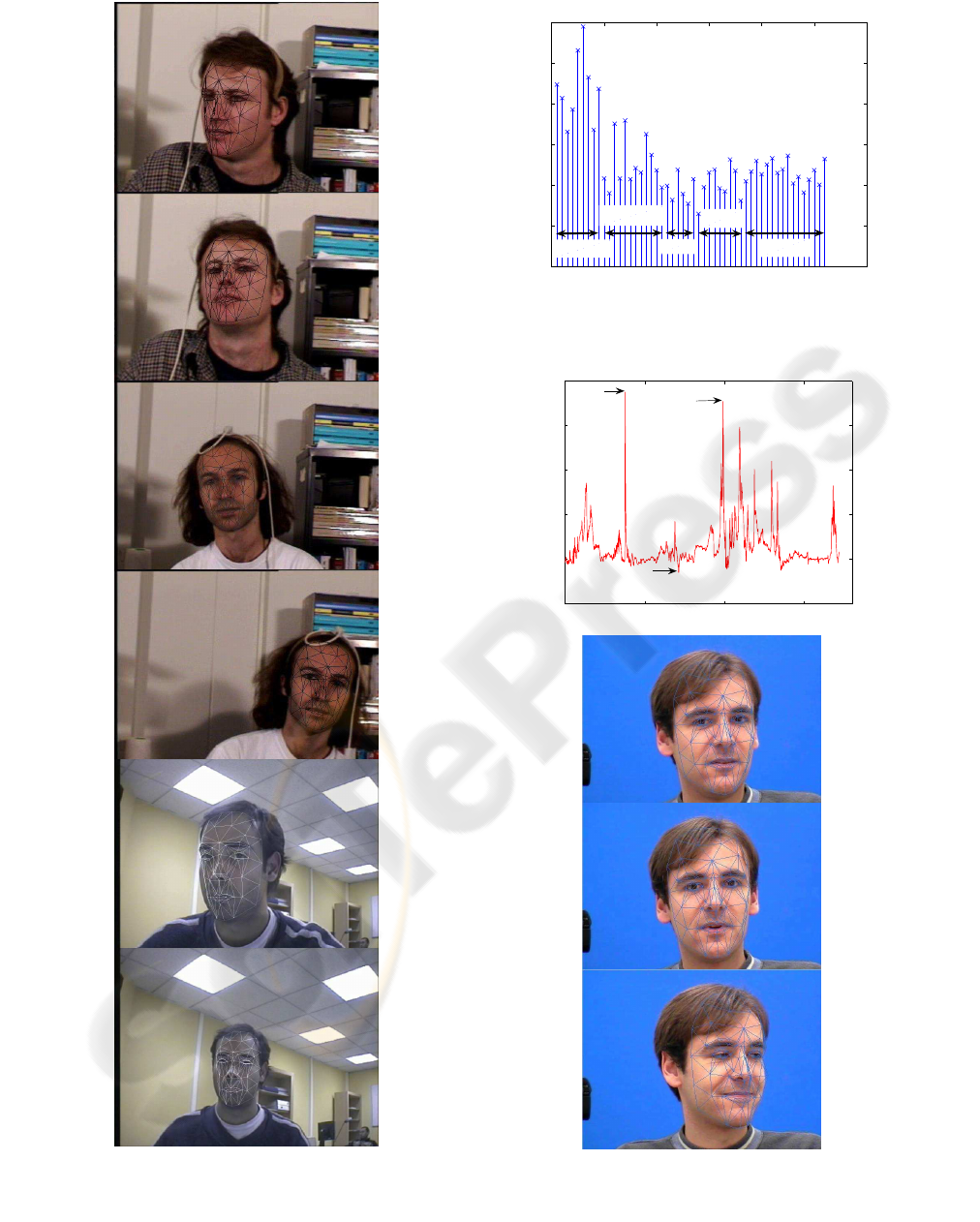
Figure 4: Results from tracking three video sequences using
the CCA algorithm in the first five images, and the KCCA
algorithm in the last one.
0 10 20 30 40 50 60
0
1
2
3
4
5
6
Point number
Standard deviation
Contour
Eyebrows
Eyes
Nose
Mouth
Figure 5: Standard deviation of the points provided for the
talking face video sequence.
0 500 1000 1500
6
8
10
12
14
16
frame
Point to point error
378
991
712
Figure 6: Mean point to point error, and three frames of the
sequence corresponding, to frame 378 to frame, 712, and
991 respectively, using the CCA algorithm.
