
2DOF POSE ESTIMATION OF TEXTURED OBJECTS WITH
ANGULAR COLOR COOCCURRENCE HISTOGRAMS
Thomas Nierobisch and Frank Hoffmann
Chair for Control and Systems Engineering, Department of Electrical Engineering and Information Technology
Universit
¨
at Dortmund, Germany
Keywords:
2DOF pose estimation, color cooccurrence histogram, probabilistic neural network
Abstract:
Robust techniques for pose estimation are essential for robotic manipulation and grasping tasks. We present a
novel approach for 2DOF pose estimation based on angular color cooccurrence histograms and its application
to object grasping. The representation of objects is based on pixel cooccurrence histograms extracted from
the color segmented image. The confidence in the pose estimate is predicted by a probabilistic neural network
based on the disambiguity of the underlying matchvalue curve. In an experimental evaluation the estimated
pose is used as input to the open loop control of a robotic grasp. For more complex manipulation tasks the
2DOF estimate provides the basis for the initialization of a 6DOF geometric based object tracking in real-time.
1 INTRODUCTION
This paper is concerned with vision based 2DOF pose
estimation of textured objects based on monocular
views. Object pose estimation is an active area of
research due to its importance for robotic manipu-
lation and grasping. The literature reports two dis-
tinct approaches to solve the pose estimation prob-
lem. Model based methods rely on the extraction of
specific geometric features in the image such as cor-
ners and edges (Shapiro and Stockman, 2001). The
extracted features are then compared and related to
a known geometric model of the object. Efficient
and reliable approaches for model-based pose esti-
mation with known correspondences have been pro-
posed by (Dementhon and Davis, 1992; Nister, 2003).
The drawback of this method is the lack of robust-
ness in the extraction of distinguishable features in
particular for textured objects. In addition, feature
based methods require the solution of the correspon-
dence problem, which becomes inherently more diffi-
cult in case of occlusion and undistinguishable fea-
tures. In contrast, global appearance based meth-
ods capture the overall visual appearance of an ob-
ject (Schiele and Pentland, 1999). Neither do they
depend on the extraction of individual features nor
do they face the correspondence problem. This pa-
per follows the latter approach for robust and compu-
tationally efficient pose estimation of multi-colored,
textured objects. (Chang and Krumm, 1999) pro-
posed distance color cooccurrence histograms for ob-
ject recognition. They emphasize the conservation
of geometric information as the major advantage of
color cooccurrence histograms compared to regular
color histograms. Based on this fundamental idea,
(Ekvall et al., 2005) proposed color cooccurrence his-
tograms for object recognition as well as 1DOF pose
estimation. The angular extension of color cooccur-
rence histograms was suggested by (Nierobisch and
Hoffmann, 2004) in the context of pose estimation of
robot players (AIBO’s). In addition the 2DOF pose
estimation of objects with minimal texture and only
three distinct colors has been successfully demon-
strated. The aim of this paper is to investigate the
potential of angular color cooccurrence histograms
for 2DOF pose estimation of multi-colored, textured
objects. Recently (Najafi et al., 2006) introduced a
method that combines appearance and geometric ob-
ject models in order to achieve robust and fast object
detection as well as 2DOF pose estimation. Their ma-
jor contribution is the integration of the known 3D
geometry of the object during matching and pose es-
timation by a statistical analysis of the distribution
of feature appearances in the view space. Nonethe-
52
Nierobisch T. and Hoffmann F. (2007).
2DOF POSE ESTIMATION OF TEXTURED OBJECTS WITH ANGULAR COLOR COOCCURRENCE HISTOGRAMS.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IU/MTSV, pages 52-59
Copyright
c
SciTePress

less their approach requires a 3D model of the object,
which is difficult to generate for objects of complex
shape.
This paper is organized as follows: Section II
provides an introduction to color cooccurrence his-
tograms with the focus on the angular extension of
the representation. Section III explains the significant
steps of segmentation and 2DOF rotation estimation
based on color cooccurrence histograms. Section IV
introduces a method to predict the confidence in the
2DOF rotation estimation. Experimental results for
pose estimation of textured objects are presented in
Section V and a summary is provided in Section VI.
2 COLOR HISTOGRAMS
0
1
2
3
4
5
6
7
B\B
<=45°
R/B
<=45°
R/R
<=45°
B/B
>45°
R/B
>45°
R/R
>45°
Frequency
Red-blue pixel pair <= 45°
Red-blue pixel pair >45°
45° Boundary
Reference pixel
Figure 1: Angular Color Cooccurrence Histogram.
Standard color histograms are often used to capture
and abstract the appearance of objects and environ-
ments, e.g. for localization tasks (Ulrich and Nour-
bakhsh, 2000). The drawback of conventional color
histograms is that geometrical information about the
color distribution is lost in the compression. As a
remedy to this detriment (Chang and Krumm, 1999)
introduce the color cooccurrence histograms (CCHs),
which summarize the geometric distribution of color
pixel pairs within the image of an object. An exten-
sion of CCHs are angular or distance color cooccur-
rence histograms (ACCHs or DCCHs, respectively),
which contain additional geometric information by ei-
ther including the orientation of a pixel pair or its dis-
tance. A CCH computes pixel pairs in a local envi-
ronment by starting at a reference. These pixel pairs
describe the color information of the reference pixel
in conjunction with all other pixels in its local en-
vironment. By linearly shifting the reference pixel
and its local environment pixel by pixel a geomet-
ric color statistics of a region of interest (ROI) is ob-
tained. In order to render the representation indepen-
dent of scale and size the histogram is normalized.
ACCHs augment the geometrical information in com-
parison to CCHs by additionally storing the orienta-
tion of the vector connecting the two pixels. Starting
from the reference pixel the angle between the ref-
erence frame and a pixel in the local environment is
computed and mapped on to a discrete set of angular
intervals. Accordingly, DCCHs include statistics on
discrete distances between pixels rather than angles.
Figure 1 illustrates the method of ACCHs calculation
for an image with only two distinct colors. The an-
gular range is discretized into two segments, below or
above 45°. Therefore, the histogram consists of six
separate bins, namely blue-blue, blue-red and red-red
pixel pairs at two distinct angles. The pose estimate
relies on the similarity between the stored histograms
of known poses with the histogram of the object with
unknown pose. Let h(d,a,b) denote the normalized
frequency of color pixels with the discrete colors a
and b oriented at a discrete angle d. The similarity of
two normalized ACCHs is defined as
s(h
1
,h
2
) =
D
∑
d=1
C
∑
a=1
C
∑
b=1
min(h
1
(d, a, b), h
2
(d, a, b)), (1)
where h
1
denotes the angle color histogram of the seg-
mented patch in the test image and h
2
is the histogram
of a training image stored in the database. D corre-
sponds to the number of angular discretizations and C
characterizes the number of distinct colors in the his-
tograms. To obtain a scale invariant similarity mea-
sure, termed match value in the remainder of this pa-
per, the histogram counts are normalized by the size
of the ROI histogram #h
1
,
m(h
1
,h
2
) =
s(h
1
,h
2
)
#h
1
. (2)
3 2-DOF ESTIMATION OF
OBJECTS WITH TEXTURE
3.1 Experimental Setup
A 5-DOF manipulator and a turntable are used to au-
tomatically generate object views at constant distance
between camera and object across a view hemisphere.
The reference views cover the upper hemisphere, for
which due to the limited workspace of the manipula-
tor the elevation is restricted to a range from 45° to

90°. In the following the elevation is denoted by θ
and the azimuth by ϕ. Figure 2 shows the setup for
capturing sample images and indicates the view point
range. Prior empirical evaluations suggest that a suc-
Figure 2: Setup for generating spherical views of the object.
cessful open loop grasp requires an accuracy of 10°
in θ and 20° in ϕ for the reference pose. Larger pose
estimation errors result in a failure of the open loop
grasping controller. Therefore, our performance mea-
sure considers angular errors in θ above 10° and in ϕ
above 20° as failures.
3.2 Object Recognition and 1-D Pose
Estimation
In (Ekvall et al., 2005) the authors present an ap-
pearance based method for robust object recognition,
background segmentation and partial pose estimation
based on CCHs. The approach employs a winner-
take-all-strategy in which the appearance of an object
of unknown pose is compared with a set of training
images of known pose. The pose associated with the
best matching training image predicts the azimuth ori-
entation of the object around the vertical axis. This
prior, incomplete 1DOF pose estimate is subsequently
augmented to a complete 6DOF pose by a feature
based technique that facilitates a geometric model of
the object. In experimental evaluations the average
angular estimation error was 6°. Our work is an ex-
tension of the previous approach in that it estimates
2DOF spherical poses located on a hemisphere. In
addition to the azimuth estimate it also considers the
elevation of the camera along the hemisphere. For
typical objects with a small top surface the varia-
tion of colors along the elevation angle is substan-
tially smaller than for rotations around the vertical
axis. Due to this property standard CCHs are un-
able to capture variations of the object’s appearance
at large elevation angles. This observation motivates
the application of ACCHs for the task of 2DOF pose
estimation. Our approach employs the same scheme
proposed by (Ekvall et al., 2005) for object recogni-
tion and background segmentation to determine the
ROI prior to the CCH computation itself. For object
recognition the image is first scanned and a matching
vote indicates the likelihood that the window contains
the object. Once the entire image has been searched,
the maximum match provides an hypothesis of the ob-
jects location. For background segmentation the best
matching window is iteratively expanded by adjacent
cells to obtain the final ROI. In a region growing
process neighboring cells that bear sufficient resem-
blance with the object’s CCH are added to the ROI.
3.3 2-D Pose Estimation
The purpose of this work is to analyze extended CCHs
for the task of 2DOF pose estimation. We assume that
the object stands on a planar, horizontally oriented
surface and the elevation and azimuth of the eye-in-
hand manipulator configuration relative to the object
are unknown. From geometric reasoning it is straight-
forward to identify the type of color cooccurrence his-
togram (CCH, ACCH or DCCH) which captures the
geometric information relevant for 2DOF rotation es-
timation. CCHs do not contain sufficient information
to discriminate between arbitrary poses, as they only
count the frequency of pixel pairs but not their rel-
ative orientation. In case of a birdseye perspective
(θ = 90°) a rotation of the object along the vertical
axis (ϕ) does not alter the frequency of color pairs in
the CCH. The same observation applies to DCCHs, as
they do not capture the orientation of the vector con-
necting the two pixels. Obviously, the rotation along
the vertical axis does not change the frequency of the
color pixels but only their orientation. Therefore AC-
CHs seem most suitable for 2DOF pose estimation as
they are sensitive to variations in appearance that are
purely related to the orientation of pixels.
In an experimental evaluation, object views are gener-
ated by moving the camera along the vertical axis (ϕ)
in 10° steps from 0° to 360° and along the horizon-
tal axis (θ) from 0° to 180° in 10° steps. To analyze
the potential of ACCHs independent of the problem
of proper background segmentation, the algorithm is
evaluated on a set of views of a textured object in front
of a homogeneous background that allows near op-
timal object segmentation. Compared to the 1DOF
pose estimation based on CCH’s the 2DOF results are
more susceptible to segmentation errors, because the
same amount of information is available to extract two
degrees of freedom rather than one. Due to the addi-
tional angular resolution of the histogram the num-
ber of bins in an ACCH is a magnitude larger than
for a CCH with the same set of colors. Therefore,
the statistics of bin counts in an ACCH deteriorates
in comparison to a CCH because the same number of
pixel pairs is distributed over a larger number of bins.
Figure 3 shows two match value responses across
StoredHistograms
0 36 72 108 144 180 216
0
0.2
0.4
0.6
0.8
1
0.88
0.890.89
0.91
0.92
0.87
0.93
Theta=0° Theta=90°Theta=75°Theta=15° Theta=30° Theta=45° Theta=60°
0 36 72 108 144 180 216
0
0.2
0.4
0.6
0.8
1
0.93
0.87
0.91
0.81
0.82
0.83
0.83
Theta=0° Theta=15° Theta=30° Theta=45° Theta=60° Theta=75° Theta=90°
Match value
Match value
Figure 3: Upper) Match value curve using the local neigh-
borhood for ACCH’s Calculation. Lower) Match value
curve using a modified approach for ACCH’s Calculation.
the training set of image-pose pairs for a test object
oriented at a true pose of approximate 183° in ϕ and
0° in θ direction. The training images are ordered in
the sequence {[θ = 0°, ϕ = 0°], [θ = 0°, ϕ = 10°], ...,
[θ = 0°, ϕ = 350°], [θ = 15°, ϕ = 0°], ..., [θ = 30°,
ϕ = 0°], ..., [θ = 90°, ϕ = 350°]}.
The match value plot is partitioned into seven slices,
each slice corresponding to a full scan along the az-
imuth ϕ in [0...360]° along seven different elevations
of θ in 0°, 15°, 30°, 45°, 60°, 75° and 90°. The
shape of the match value response resembles an am-
plitude modulated signal. The slower modulation cor-
responds to the horizontal rotation, whereas the faster
modulation contains the information about the verti-
cal rotation. The two match value responses corre-
spond to two different ways of computing the ACCH.
In the upper match value response pixel pairs origi-
nate from a local neighborhood region of the refer-
ence pixel. Local color pair statistics are useful to
distinguish between multicolored objects with a fair
amount of texture. The local statistics results in an
ambiguity along the θ rotation because the slow mod-
ulation does not discriminate well enough to ensure
a robust estimation. In our example the variation in
maxima along θ only ranges from 0.93 to 0.87. Pixel
pairs counted across a larger separation contribute
more information on the object’s pose. Nearby pixel
pairs, even though useful for object recognition, di-
lute the information of the object’s global appearance
as e.g. the likelihood of finding a same colored pixel
next to the reference pixel is fairly large. Therefore,
the second scheme only counts pixel pairs separated
by a minimal distance and ignores pixels in the imme-
diate neighborhood of the reference pixel. As a result
the 2DOF appearance of the object reflected through
the ACCHs becomes more distinguishable. In this
scheme the variation in maxima along θ ranges from
0.93 to 0.81, with a significant decrease in the ampli-
tude of incorrect local maxima. The drawback is that
due to the definition of an excluded neighborhood re-
gion the scheme is no longer scale-invariant. There-
fore, the second approach is only feasible if the rela-
tive distance between the camera frame and the object
is approximately known in order to properly scale the
excluded region.
The test set contains 190 test images with random
2DOF poses that differ from the training set. The
mean angular error across the vertical axis is about
10° and 3.8° across the horizontal axis. The ACCHs
operate with a resolution of 12 discrete angles and 40
colors. The local environment comprises 20 pixels,
but only pixel pairs with a separation of more than 10
pixels contribute to the angular histograms.
4 CONFIDENCE RATING
Our experiments indicate that the major problem for
reliable appearance based 1DOF or 2DOF pose esti-
mation in natural scenes is the accuracy of the seg-
mentation in the preprocessing stage. In most cases
the 1DOF rotation estimation is fairly robust towards
segmentation errors. However if background objects
of similar colors are located next to the object the seg-
mentation partially or completely merges the two ob-
jects. Incorrect segmentation results in poor perfor-
mance of the subsequent pose estimation due to the
large amount of background noise introduced by the
misleading object. In order to detect such incorrect
rotation estimates we rate the confidence in an esti-
mate based on the characteristics of the match value
response. Estimates that originate from ambiguous
match value responses with multiple local maxima of
similar magnitude are rejected. A multi-layered feed-
forward neural network is trained on match value re-
sponses which an expert previously manually classi-
fied by visual inspection as either ambiguous or reli-
able. The match value responses constitute the input
vector x
n
, based on which the neural network rates
the confidence in terms of a probability h(x
n
) that the
estimate is reliable. The input vector x
n
corresponds
to the match values of the test image over the set of
training images. The training method is similar to the
well known backpropagation algorithm, except that in

this case gradient descent minimizes the entropy
E
min
= min
w
ij
−
N
∑
n=1
d
n
ln(h(x
n
)) + (1− d
n
)ln(1− h(x
n
))
(3)
rather than the squared error (MacKay, 1992). The
term d
n
∈ {0,1} denotes the expert reliability clas-
sification of the training example x
n
. The term w
ij
denotes the synaptic weights that are subject to op-
timization. The entropy in Eq. 3 acquires its min-
imum, if h(x
n
) is equal to the relative frequency of
training pairs c(x
n
,d
n
= 1)/c(x
n
,d
n
= {0,1}). The
classifier reject any rotation estimates with an am-
biguous match value response x for which the neural
network predicts a confidence lower than h(x) < 0.8.
For the example shown in the left of figure 4 the rota-
Figure 4: Left top) overlapping objects merged during seg-
mentation. Left bottom) corresponding flat match value re-
sponse due to incorrect segmentation. Right top) proper
segmentation from a different perspective. Right bottom)
corresponding match value curve with an unique maximum.
tion estimation fails because the segmentation merges
a part of book with similar colors with the object of
interest in the foreground. As a result of the poor ob-
ject segmentation the rotation estimate has an error of
about 60°. However, the neural network rejects this
rotation estimation due to its low confidence rating
of h(x) = 0.69 caused by the incorrect segmentation.
The corresponding flat match value curve shows two
local maxima of similar magnitude. in response to the
rejection, the manipulator moves the camera to a dif-
ferent pose in order to capture an image of the object
from a better perspective. In the new image shown
on the right side of figure 4 the two objects no longer
overlap and the segmentation succeeds. The rotation
estimation error is less than 20° which is sufficient
for the subsequent model based refinement step. The
corresponding match value response shows a unique
maximum, which the neural network confirms with a
high confidence rating h(x) = 0.98.
The confidence rating of the 2DOF pose estimate
is based on the ambiguity of the match value response.
In order to distinguish between reliable and unreli-
able estimates, a neural network is trained on manu-
ally classified match value responses. In order to train
the neural network a small subset of features from the
match value response that best correlate with the clas-
sification has to be selected. From inspection of ex-
ample responses it turns out, that the distribution and
magnitude of global and local maxima are suitable
features to predict the confidence.
Figure 5 shows a blue-colored box in the follow-
ing referred to as object A after being segmented from
the background. The pose estimation error in front of
the blue background is about 2° in θ and about 46°
in ϕ. The large pose estimation error in ϕ is caused
by the imperfect segmentation of the blue object from
the blue background. The error in front of the yel-
low background that is easier to separate from the ob-
ject only amounts to 2° in θ and 6° in ϕ. In the fol-
lowing we analyze the causes for incorrect pose es-
timates and how to detect potential outliers from the
match value response itself, so that these unreliable
pose estimates can be rejected beforehand. The cor-
Figure 5: Fruitbox under different background conditions.
responding match value responses of object A for the
two background scenarios are shown as a 2D-plot (up-
per graphs) and 1D folded plot (lower graphs) in fig-
ure 6. The left top graph shows the ambiguous match
value response with several local maxima of similar
magnitude caused by poor segmentation in front of
the blue background. The noise introduced into the
ACCH by the blue background pixels is reflected by
the bimodal distribution in ϕ. In analogy to figure 3
the upper left graph shows the slow modulation corre-
sponding to the changes of θ and the fast modulation
corresponding to ϕ. The stars denote local maxima
of the response which magnitude exceeds a thresh-
old of 95 % relative to the global maximum. Addi-
tionally also the local maxima along the θ slices are
marked by stars in case exceeding 97 % of the abso-
lute maximum. Obviously, several local maxima of
similar magnitude in the first slice might correspond
to the true object pose in ϕ.
The right part of figure 6 shows the 2D and 1D
match value responses for the image with proper ob-

ject background segmentation. The 2D match value
shows a unique maximum. In the 1D folded represen-
tation the local maxima are either in the vicinity of the
global maximum or correspond to similar values of ϕ
at different values of θ.
Based on this empirical observation the neural net-
work predicts the confidence based on the following
four features extracted from the match value response:
1. R
ϕ
: ratio between the magnitude of the global
maximum and the second best match value out-
side a minimum separation of 20 ° within the same
θ slice that contains the global maximum
2. D
ϕ
: separation between the global maximum and
the second best match outside the minimum sep-
aration within the same θ slice that contains the
global maximum
3. R
θ
: ratio between the magnitude of the global
maximum and the second best match value across
all θ slices
4. D
θ
: separation between the magnitude of the
global maximum and the second best match value
across all θ slices
The purpose of the first two features is to detect an
ambiguous response in ϕ, the other two features dis-
tinguish between ambiguous and disambiguous re-
sponses in θ. Notice, that D
θ
is specified in terms of
an integer that denotes the number of slices that sep-
arate the first from the second maximum. A smooth
variation of the match value response with θ implies
that the second maximum should occur in the neigh-
boring slice D
θ
= 1. Larger values of D
θ
in partic-
ular in conjunction with a large ratio R
θ
indicate a
potential ambiguity in the θ estimate. The next sec-
tion reports experimental results of 2DOF pose esti-
mation and the improvement using the probabilistic
confidence rating under real world conditions.
5 EXPERIMENTAL EVALUATION
The experimental evaluation of the proposed method-
ology in realistic scenarios is based on three test ob-
jects of different color and texture with views gener-
ated for various backgrounds. The experiments in the
previous section assumed an ideal, textureless object
with three distinguishable colors in front of a homo-
geneous background. The purpose of these experi-
ments is to analyze the robustness and accuracy of the
pose estimation for daily life objects in a realistic set-
ting. The three test objects are shown in figure 7 and
are referred to in the remainder of the text as object
A, B and C. The ACCHs operate with a resolution of
10 angles and 40 colors.
Figure 7: Test objects A, B and C.
In the following
¯
E denotes the mean error of the
pose estimate in θ and ϕ. The training images belong
to views at θ angles of 45, 50, 60, 70, 80 and 90°. In ϕ
the sample images are captured in 10° steps. The min-
imal
¯
E that is feasible in theory with a winner-takes-
all strategy depends on the density of samples, in our
case it amounts to 2.5° in ϕ and 2.4° in θ. The results
in table 1 indicate that for all test objects the actual
error along θ is close to the optimum. The mean er-
ror in ϕ is significantly lower than the error bounds
for successful grasping defined in section III. The ex-
perimental results in table 1 demonstrate that under
the assumption of near optimal segmentation an er-
ror rate of less than 4° in θ and 9° in ϕ is feasible
for all test objects. This error rate is small enough
for a successful open loop grasp within the specified
error bounds. The percentage of failures is approxi-
mately 7%. Table 2 reports the results of the pose
Table 1: 2DOF pose estimation with optimal segmentation.
Objects Object A Object B Object C
¯
E
(ϕ)
7.0° 8.9° 8.5°
¯
E
(θ)
4.0° 3.3° 3.7°
estimation under different background conditions and
the impact of the probabilistic confidence rating on
the failure, error and acceptance rate. Background A
consists of a wooden material and shows a yellowish
textured surface (as shown in the left image in figure
5). The two other backgrounds B and C contain a tex-
tured blue and green surface, respectively. The first
column specifies the actual object and background,
the three following columns describe the mean errors
of the pose estimation in θ and ϕ and the percentage of
failures. The next two columns show the mean error
¯
E
for θ and ϕ for those views that were accepted by the
confidence rating based on the match value response.
Finally, the percentage of failures and the rate of ac-
cepted views (FR) is provided in the last two columns.
To verify the methodology under realistic environ-
mental conditions the test set contains 50 images of
the three objects taken at random 2DOF positions for
the three different backgrounds. Based on the fact
that the color distribution of object A contains a large
portion of blue colors, segmentation errors with back-
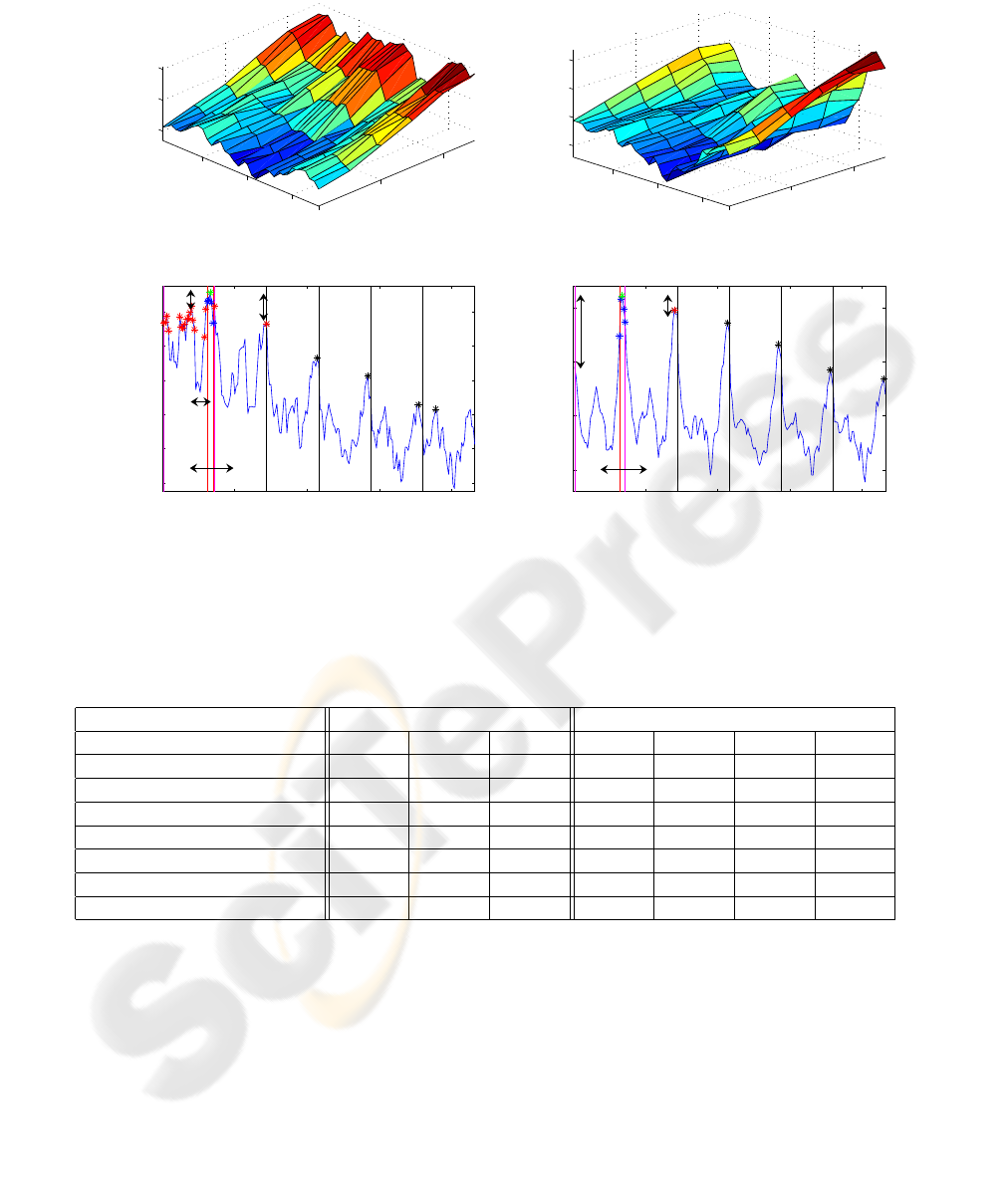
45
50
60
100
200
300
0.45
0.5
0.55
theta
phi
Match value
45
50
60
100
200
300
0.6
0.65
0.7
0.75
theta
phi
Match value
0 50 100 150 200
0.44
0.46
0.48
0.5
0.52
0.54
Match value
Histograms
0 50 100 150 200
0.6
0.65
0.7
0.75
Match value
Histograms
R
φ
R
θ
D
φ
φ
R
θ
θ
θ
D
R
D
Figure 6: Left top) Ambiguous 2D match value curve based on segmentation noise. Left bottom) According 1D match value
response based on segmentation noise. Right top) Unique 2D match value response based on proper segmentation. Right
bottom) Corresponding match value response with an unique maximum.
Table 2: 2DOF pose estimation for the three objects under different background conditions.
Object / Background pose estimation pose estimation with confidence
¯
E
(ϕ)
¯
E
(θ)
Failures
¯
E
(ϕ)
¯
E
(θ)
Failures FR
Object A / Backgrd. A 8.0° 11.8° 44% 5.3° 7.3° 27% 30%
Object A / Backgrd. B 22.2° 14.7° 66% 11.2° 9.8° 47% 34%
Object A / Backgrd. C 9.0° 7.2° 20% 4.6° 4.0° 0% 32%
Object B / Backgrd. A 9.1° 15.8° 42% 7.4° 9.2° 19% 42%
Object B / Backgrd. B 10.7° 25.7° 68% N.A. N.A. N.A. N.A.
Object C / Backgrd. A 12.4° 30.2° 72% 6.1° 19.5° 42% 15%
Object C / Backgrd. B 6.5° 9.1° 28% 4.8° 5.3° 11% 36%
ground B cause a substantial error
¯
E for θ as well as
ϕ. The results in table 2 demonstrate that for simi-
lar object-background colors the color information in
a CCH alone provides an insufficient cue for object
segmentation and pose estimation. One possible rem-
edy to this problem is to integrate additional cues in
the segmentation process. The distance between cam-
era and object or background pixels can be estimated
from optical flow or stereo-vision across multiple im-
ages taken from slightly different views. It is expected
that the segmentation accuracy improves substantially
if additional cues are integrated. The objective of the
confidence rating is to gain accuracy in the pose esti-
mate, in particular to reduce the number of failures at
the cost of rejecting ambiguous object views. In the
context of robotic object grasping robust estimation
is more important than complete decision making. It
is acceptable to reject an ambiguous view and to de-
fer temporarily the grasping process. The manipulator
moves the camera to novel viewpoints until the algo-

rithm generates a pose estimate supported with suffi-
cient confidence. For object A the two backgrounds A
and C are less problematic in terms of segmentation
noise rejection of uncertain poses reduces the mean
error as well as the number of failures. In case of
background C the neural network is able to exclude
all failures, albeit at the cost of rejecting two out three
views. Notice, that for test object B in front of back-
ground B that coincides with the object color nearly
70% of the original estimates are failures. In this case
the neural network ultimately classifies all estimates
as unreliable. Acceptable error and failure rates are
achieved for test object C in front of background B.
The mean estimation error
¯
E is small enough to al-
low an open loop grasp for 9 of 10 estimations. In
contrast pose estimation on background A fails al-
most completely with an failure rate of 72% due to
the similar colors of the object. Even if only 15 %
of the estimates are accepted, the failure rate of 42%
is still not acceptable. Instead of an open loop grasp
control based on a single image and pose estimate it
is more robust to operate in feedback mode by ac-
quiring additional images. A Kalman filter approach
fuses observed pose estimates with the known camera
motions. The experimental results demonstrate that
2DOF pose estimation based on ACCHs is feasible
under the assumption of proper segmentation. The
main drawback of the proposed method is the sensi-
tivity with respect to noise and segmentation errors.
As a 2DOF pose estimation with ACCHs is substan-
tially more difficult, the approach does not achieve the
same level of robustness as in the case of 1DOF pose
estimation based on pure CCHs.
6 CONCLUSIONS
In this paper we presented a novel approach for 2DOF
pose estimation based on angular cooccurrence his-
tograms. Under the assumption of proper object back-
ground segmentation the accuracy of estimated poses
is sufficient for object manipulation with a two-finger
grasp. The confidence rating of the match value re-
sponse by the neural network is a suitable means to
further improve the robustness of pose estimation at
the cost of a reduced recognition rate. The quality of
the appearance based segmentation deteriorates sub-
stantially in the case of overlapping objects or back-
grounds with similar colors. The degradation reflects
itself in an ambiguous match value curve detected by
the neural network. In a robotic manipulation sce-
nario the camera is moved in order to capture an im-
age of the object from a presumably better perspec-
tive. The grasping motion is not executed until a suffi-
cient confidence in the prior pose estimation has been
achieved. Our experimental results show that earlier
appearance based methods for 1 DOF pose estimation
can be extended to a 2DOF pose estimation. How-
ever, 2DOF pose estimation based on ACCHs is no
longer scale invariant and therefore requires an ap-
proximate initial estimate of scale. For our task the
reach of the robot arm is limited so that the scale does
not vary much across different configurations. There-
fore, a single training set of ACCHs captured at an
intermediate camera to object range is valid across
the entire workspace of the manipulator. An avenue
for future research is the integration of appearance
based approaches with an image based visual servo-
ing scheme. In image based visual servoing the cor-
respondance problem is prevalent in particular if are
only partially visible. To solve the correspondence
problem for visual servoing tasks the objects are of-
ten labeled with artificial landmarks like color blobs.
These approaches are therefore constrained to struc-
tured, synthetic environments. To overcome all those
limitations visual servoing is established on the entire
appearance of an object.
REFERENCES
Chang, P. and Krumm, J. (1999). Object recognition with
color cooccurrence histograms. In CVPR’99,pp. 498-
504.
Dementhon, D. and Davis, L. (1992). Model-based object
pose in 25 lines of code. In ECCV.
Ekvall, S., Kragic, D., and Hoffmann, F. (2005). Ob-
ject recognition and pose etimation using color cooc-
curence histograms and geometric modeling. In Image
and Vision Computing.
MacKay, D. (1992). The evidence framework applied to
classification networks. In Neural Computation, Vol.
4, 720-736.
Najafi, H., Genc, Y., and Navab, N. (2006). Fusion of 3d
and appearance models for fast object detection and
pose estimation. In Asian Conference on Computer
Vision.
Nierobisch, T. and Hoffmann, F. (2004). Appearance based
pose estimation of aibo’s. In International IEEE Con-
ference Mechatronics & Robotics, Proceedings Vol.3,
pp. 942-947.
Nister, D. (2003). An efficient solution of the five-point
relative pose problem. In CVPR.
Schiele, B. and Pentland, A. (1999). Probabilistic object
recognition and localization. In ICCV’99.
Shapiro, L. and Stockman, G. (2001). In Computer Vision.
Prentice Hall.
Ulrich, I. and Nourbakhsh, I. (2000). Appearance-based
place recognition for topological localization. In IEEE
ICRA, San Francisco, pp. 1023-1029.
