
MODELING WITH CURRENT DYNAMICS AND VIBRATION
CONTROL OF TWO PHASE HYBRID STEPPING MOTOR IN
INTERMITTENT DRIVE
Ryota Mori, Yoshiyuki Noda, Takanori Miyoshi, Kazuhiko Terashima
Department of Production Systems Engineering, Toyohashi University of Technology
Hibarigaoka 1-1, Tempaku, Toyohashi, 441-8580, Japan
Masayuki Nishida, Naohiko Suganuma
Tokyo Weld Co., Ltd.
Ashitaka 292-50, Numazu, Shizuoka, 410-0001, Japan
Keywords:
Stepping motor, phase plane analysis, vibration control.
Abstract:
This paper presents modeling of stepping motor and control design of input pulse timing for the suppression
control of vibration. The stepping motor has the transient response of electric current for the pulse input.
Therefore, the motor model considering the transient response of the current is built. The validity of the
proposed model is verified by comparing the model considering the transient response of the current with
the one without its consideration. Design of the pulse input timing in the method of the four pulse drive is
realized to achieve the desired angle without vibration and overshoot using an optimization method. Finally,
the effectiveness of the proposed method is demonstrated by comparing simulation results with experiments.
1 INTRODUCTION
The stepping motor has been widely used for factory
automation (FA) and office automation (OA) equip-
ment, because it is able to realize high-accuracy posi-
tioning by an open loop control. It is used also for the
production process of electronic parts, and then the
settling time of the stepping motor is directly linked
to the productivity. Therefore, the high speed and the
low vibration are strongly desired in the production
line. However, the stepping motor vibrates around the
neighborhood of the equilibrium points owing to the
step-wise drive from the viewpoints of the motor char-
acteristics. To dampen the vibration of motor, (i) mi-
cro step drive method that makes changes the exciting
current change in details, and (ii) a inverse phase exci-
tation dumping, and (iii) a delay damping method, are
proposed(D.Ebihara and T.Iwasa, 1984). Especially,
the micro step drive is possible to drive with the low
vibration. Because it is made to drive by changing
at smaller angle than the basic step angle by making
the exciting current change in details (D.Ebihara and
T.Iwasa, 1984)D It is necessary to give the excitation
instruction considering the dynamic characteristic of
the system in the transient state of the start and the
stop times. As an adjustment method of the excita-
tion sequence, the method of applying a lowpass filter
as a pre-compensator (T.Miura et al., 2000), and the
method that uses the genetic algorithm (T.Miura and
T.Taniguchi, 1999) are proposed. The vibration con-
trol considering robustness for the vibration of the in-
ertia load is studied by these methods. Moreover, the
technique for decreasing the resonance using the posi-
tion and the speed feedback estimated by the observer
is given (S.M.Yang and E.L.Kuo, 2003).
The stepping motor has a strong nonlinearity.
Therefore, when the linear control theory is applied, it
is often linearized around the equilibrium point. How-
ever, the operation area of the stepping motor is wide,
so variable control gain is necessary to keep an excel-
lent control performance. Whereas, the method us-
ing an exact linearization by means of nonlinear feed-
back and coordinate transformation of state space is
proposed (M.Bodson et al., 1993). Moreover, the ap-
plication of the control algorithm of the artificial in-
telligence system such as fuzzy theory (F.Betin and
D.Pinchon, 1998) and neural network (K.Laid et al.,
2001) are provided.
Those control methods are mostly discussed con-
cerning with a step drive and a continuous drive.
However, the high speed and the high accurate po-
sitioning system by the fine drive might be requested
in the FA equipment. In this case, the positioning by
a few number of pulse order is performed.
388
Mori R., Noda Y., Miyoshi T., Terashima K., Nishida M. and Suganuma N. (2007).
MODELING WITH CURRENT DYNAMICS AND VIBRATION CONTROL OF TWO PHASE HYBRID STEPPING MOTOR IN INTERMITTENT DRIVE.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 388-393
DOI: 10.5220/0001651303880393
Copyright
c
SciTePress
Therefore, in this paper, the vibration suppression
is studied when the stepping motor is intermittently
driven by a predetermined few number of step, assum-
ing FA application. The response of the stepping mo-
tor is varied by the influence of transient response of
the current, when the command pulse interval is rather
short for the excitation phase. Therefore, a mathe-
matical model comprised of the torque equation with
the dynamics of the current in the generated torque
is presented. By means of the phase plane analysis
and the optimization for the obtained mathematical
model, the pulse control timing with a low vibration is
obtained. The validity of the proposed model is con-
firmed through the experiments and the simulations.
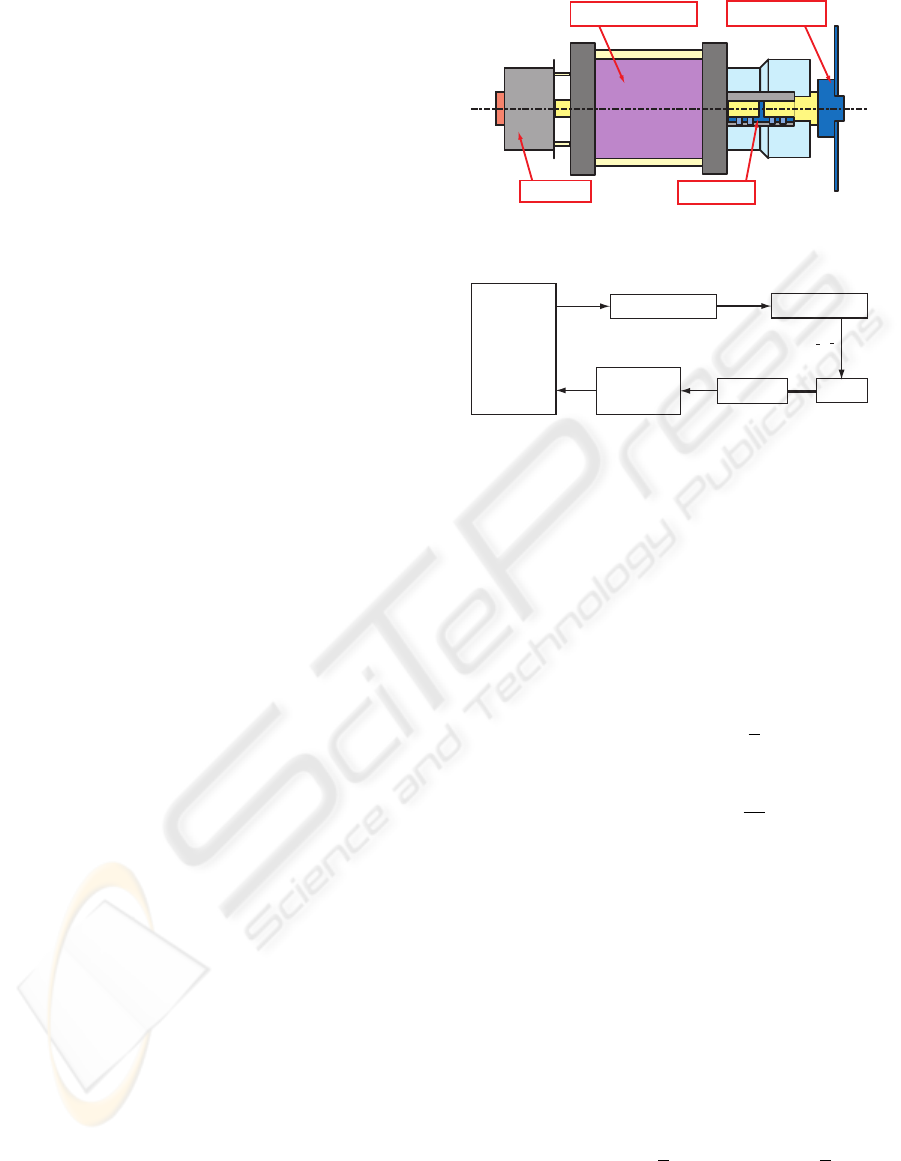
2 EXPERIMENTAL SETUP
The experimental setup consists of motor with the in-
ertia load connected with a solid shaft as shown in
Figure 1. The shaft has been extended from both ends
of the motor, and the inertia load is installed in a one
end. The encoder has been installed to the shaft on
the other side.
The block diagram of the driving system of a step-
ping motor is shown in Figure 2. The motor driver
uses the commercial item, and the motor is driven up
to the fixed current drive in a full step. The pulse in-
put is carried out by the designed timing in advance by
numeric calculation. The pulse is outputted according
to the timing specified from the Pulse Oscillator. The
excitation current is passed by excitation phases by
the motor driver, and the motor is driven. The excita-
tion phase of the motor can be switched by the pulse
being input from Pulse Oscillator to Motor Driver. In
this study, the motor is used with the excitation phase
comprised of Phase A, Phase B, Phase
¯
A, and Phase
¯
B. The excitation phase switches in order of AB →
B
¯
A →
¯
A
¯
B →
¯
BA → AB by two phase excitation. The
rotor angle is detected by the encoder of accuracy of
36000[pulse/rev]. The encoder signal is doubled by
up-down counter of four.
3 STEPPING MOTOR MODEL
3.1 Modeling of Stepping Motor
The stepping motor rotates stepwise by switching the
excitation phase by input pulse. Therefore, Eq.(1) can
be derived from the equation of motion of rotation
system (D.Ebihara and T.Iwasa, 1984).
J
¨
θ+ D
˙
θ+ T
L
= T
M
(1)
Stepping motor
Encoder
Inertia load
Coupling
Figure 1: Construction of stepping motor.
Controller
PIC 18F252
Pulse oscillator Motor driver
Encoder
Counter
PIC 18F252
Motor
iA,iB,iA,iB
θ
Figure 2: Block diagram of driving system for a stepping
motor.
,where J is an inertia moment, D is a damping coeffi-
cient, T
L
is a load torque, T
M
is the generated torque
of motor and θ shows a rotor angle. The generated
torque can be described as the sum of the generated
torque of each phase. The generated torque of each
phase of two phase hybrid stepping motor is repre-
sented by the following equations.
T
A
= −i
A
Ksin(N
R
θ) (2)
T
B
= −i
B
Ksin(N
R
θ−
π
2
) (3)
T
¯
A
= −i
¯
A
Ksin(N
R
θ−π) (4)
T
¯
B
= −i
¯
B
Ksin(N
R
θ−
3π
2
) (5)
,where K is a torque constant, N
R
is the number of a
rotor teeth and, i
A
, i
B
, i
¯
A
and i
¯
B
are excitation current
of each phase. The suffix of torque T and current i
shows phase A, B,
¯
A and
¯
B respectively. Whenever
the pulse is input in the two phase stepping motor,
it is excited in order of AB → B
¯
A →
¯
A
¯
B →
¯
BA →
AB. Moreover, because i
A
= −i
¯
A
and i
B
= −i
¯
B
, then
it follows that T
A
= T
¯
A
and T
B
= T
¯
B
. Therefore the
generated torque T
M
becomes the sum of T
A
and T
B
. If
a magnetic axis is defined as θ = 0 when phase A and
phase B are the excited states, the generated torque is
shown as follows.
T
M
= −i
A
Ksin(N
R
θ+
π
4
) −i
B
K sin(N
R
θ−
π
4
) (6)
Generally, it becomes i
A
= i
B
= i at the fixed cur-
rent drive. And Eq.(7) is derived by the trigonometric
function formula.
MODELING WITH CURRENT DYNAMICS AND VIBRATION CONTROL OF TWO PHASE HYBRID STEPPING
MOTOR IN INTERMITTENT DRIVE
389
T
M
= −
√
2iKsin(N
R
θ) (7)
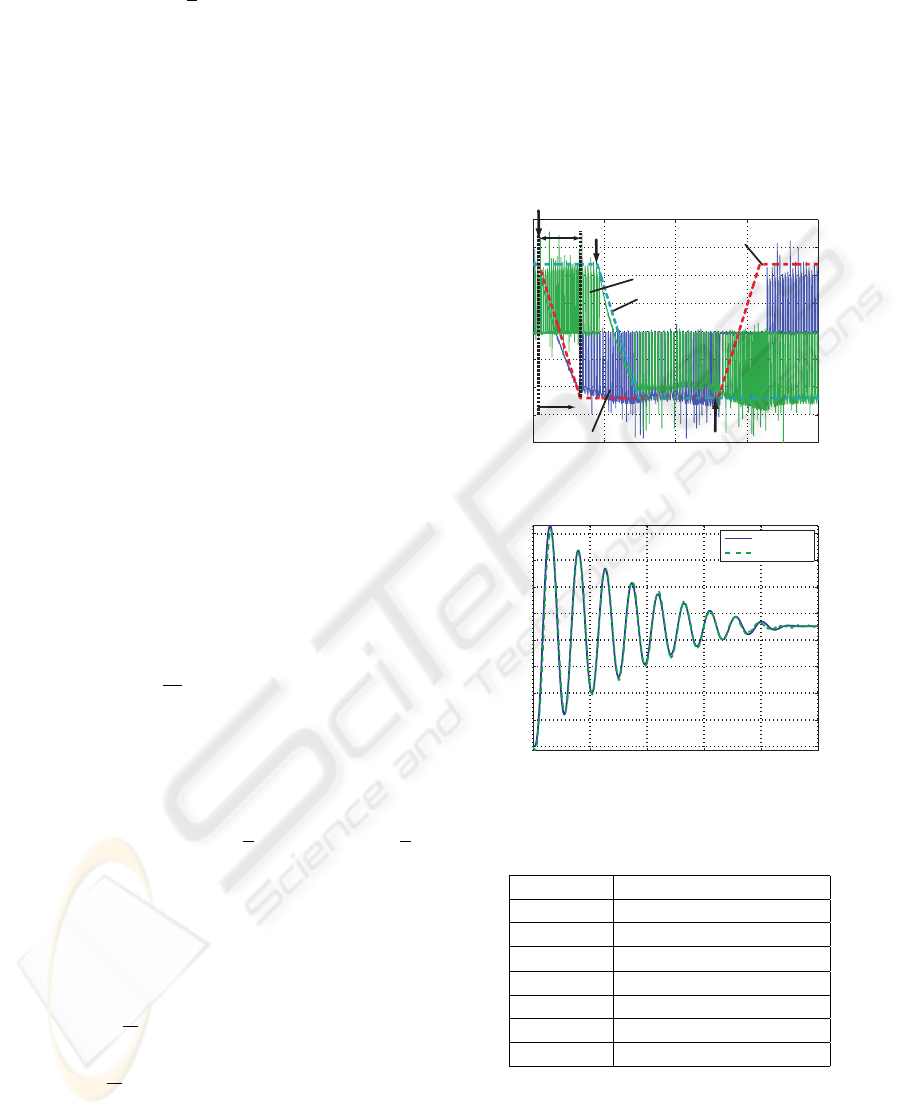
This formulation is explained by the reference of
D.Ebihara and T.Iwasa, 1984. However, there is a
transient state between the time of the pulse input
and the switching time of the current of the excitation
phase, as shown in Figure 3. Here, Figure 3 shows the
excitation current transition of each phase after pulse
input when the stepping motor is driven, and Exp I
A
is a current of phase A and
¯
A, Exp I
B
is a excitation
current of phase B and
¯
B, Sim I
A
and Sim I
B
is the
assumed current in simulation. From Figure 3, when
the first pulse is input, the Exp I
A
is switched from the
plus into the minus. It is meant to change the phase
¯
A from the phase A, because Exp I
A
is the excitation
current of phase A. Here, the change of the current
in Exp I
A
is almost linearly changed from the value
of +1.2[A] to the value of −1.2[A], when the excita-
tion phase is switched. Excitation current Exp I
B
of
the phase B is also similar. Therefore, the excitation
current is thought that the current is changed almost
linearly from the input of the pulse up to the switch-
ing the excitation phase as shown in Sim I
A
and Sim
I
B
. The current response of interval T
d
[s] is shown in
Eq.8, when the elapsed time after inputting the pulse
is defined as T
i
[s], and the time from the input of the
pulse up to switching the excitation current is defined
as T
d
[s].
i
A,B
= −(1−2
T
i
T
d
)I, (0 ≤ T
i
≤ T
d
) (8)
,where I is the rated current of the motor. From
Eq.(1), Eq.(6) and Eq.(8), the equation of motion is
shown in Eq.(9).
J
¨
θ+D
˙
θ+T
L
= −i
A
Ksin(N
R
θ+
π
4
)−i
B
Ksin(N
R
θ−
π
4
)
(9)
,where i
A
is shown by the following equation. As for
i
B
, it is omitted in this paper, due to the limitation of
paper, because it is similar equation.
i
A
=
I, (Phase A)
−(1−2
T
i
T
d
)I, (Phase A → Phase
¯
A)
−I, (Phase
¯
A)
(1−2
T
i
T
d
)I, (Phase
¯
A → Phase A)
(10)
3.2 Parameter Identification
The parameter of Eq.(9) is identified from the step re-
sponse of stepping motor. The parameter is decided
to be minimized the error sum of square by a Sim-
plex Method(M.Hamaguchi et al., 1994). Here, J,
D and T
L
are the parameters including the encoder.
The step response result is shown in Figure 4. The
response corresponds with the experiments and the
simulations, and then the identification is appropri-
ate, because simulation agrees well with experimen-
tal results. The model parameter is shown in Table 1,
where α is a step angle.
0 0.001 0.002 0.003 0.004
2
1.5
1
0.5
0
0.5
1
1.5
2
Time[s]
Current[A]
Exp I
A
Exp I
B
Sim I
A
Sim I
B
1st Pulse input
2nd Pulse input
3rd Pulse input
Td
Ti
Figure 3: Current response of stepping motor.
0 0.01 0.02 0.03 0.04 0.05
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
Time[s]
Angle[deg]
Simulation
Experiment
Figure 4: Step response of proposed model.
Table 1: Motor parameters.
Parameter Value
α 0.9 [deg]
I 1.2 [A/phase]
J 164.94 × 10
−7
[kg·m
2
]
D 0.001442 [kg·m·s]
T
L
0.00357 [N·m]
K 0.2662 [N·m/A]
T
d
0.0007 [s]
3.3 Comparison Between Proposed and
Conventional Model
The conventional model is written by the following
equation using Eq.(1) and Eq.(7).
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
390
J
¨
θ+ D
˙
θ+ T
L
= −
√
2IK sin(N
R
θ) (11)
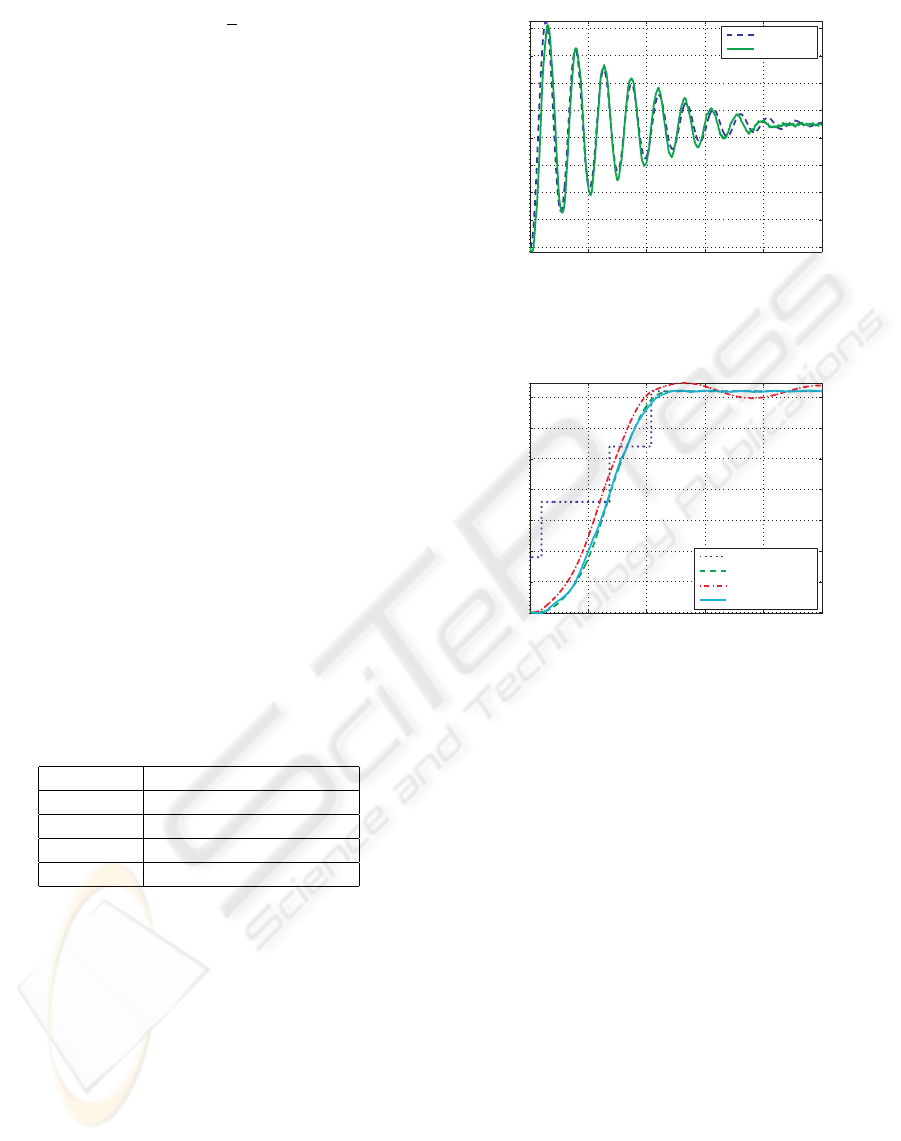
The model parameters which did not consider the
current response can be also identified from the step
response in the same way with subsection 3.2. The
parameters obtained from the optimization are shown
in Table 2. The result of the step response is shown
in Figure 5. Experiments and simulations are almost
well in agreement as shown in Figure 5
The model which did not consider the current re-
sponse is shown in Eq.(11), and the proposed model
are compared. In comparison, the response of motor
in experiment and simulation are checked, when four
times pulses are inputted to motor. T
1
[s] is the interval
of input pulse from the first pulse to the second pulse.
And T
2
[s] is the interval of input pulse from the sec-
ond pulse to the third pulse, T
3
[s] is the interval of in-
put pulse from the third pulse to the fourth pulse, and
then T
1
=400[µs]CT
2
=2331[µs]CT
3
=1428[µs]. The
pulse timing of T
1
, T
2
, and T
3
is respectively obtained
by using Simplex Method to minimize the evaluation
function as shown in Eq.(12) at Section 4. Experiment
and simulation results are shown in Figure 6.
The rising time of the conventional model is
shorter than proposed model, and the residual vibra-
tion remains close to the desired value. However, sim-
ulation result of the proposed model agrees well with
the experimental result. As a result, we confirmed that
the more highly accurate model can be obtained by
the proposed model considering the current response.
Table 2: Parameters of conventional model.
Parameter Value
J 168.56 × 10
−7
[kg·m
2
]
D 0.001505 [kg·m·s]
T
L
0.001902 [N·m]
K 0.2582 [N·m/A]
4 DESIGN OF PULSE INPUT
TIMING
In this paper, the time that the rotor reaches the de-
sired angle without vibration, when input using four
pulses are given to the stepping motor, is determined
based on the proposed model. The time of the first in-
put pulse is 0[s]. The one step angle is α = 0.9[deg],
so the desired angle by four input pulse is 3.6[deg].
The pulse interval T
1
, T
2
, and T
3
denotes the same
meaning with the preceding section. When T
1
are
changed from 300[µs] up to 2200[µs] every 50[µs] in-
terval, total 39 patterns, optimal T
2
and T
3
are decided
0 0.01 0.02 0.03 0.04 0.05
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
Time[s]
Angle[deg]
Simulation
Experiment
Figure 5: Step response of conventional model.
0 0.002 0.004 0.006 0.008 0.01
0
0.5
1
1.5
2
2.5
3
3.5
Time[s]
Angle[deg]
Reference
Proposed
Conventional
Experiment
Figure 6: Comparison result of the conventional and pro-
posed model.
in the same way. The optimization problem of mini-
mizing the following evaluation function is solved as
a decision method.
min
T
2
,T
3
J
c
= (maxθ(t) −4α)
2
, (T
1
+ T
2
+ T
3
+ T
d
≤t)
(12)
,where T
d
is the settling time of the current for the
pulse input. To minimize the overshoot at the desired
angle, a Simplex Method is used as an optimization
technique. The evaluation function is decided to be
the error square of the desired angle and the maximum
angle after reaching at around the neighborhood of the
desired angle. If the overshoot with the desired angle
is small, the vibration then is also a little, because the
stepping motor is settled at the desired angle decided
according to the excitation phase.
The overshoot of the angle in the control time ob-
tained by a Simplex Method were almost 0.0009[deg]
or less. The overshoot was less than 0.1 % against
the step angle of α = 0.9[deg] by a Simplex Method.
Therefore, it is thought that there is little overshoot.
Simulation results using control timing obtained
MODELING WITH CURRENT DYNAMICS AND VIBRATION CONTROL OF TWO PHASE HYBRID STEPPING
MOTOR IN INTERMITTENT DRIVE
391
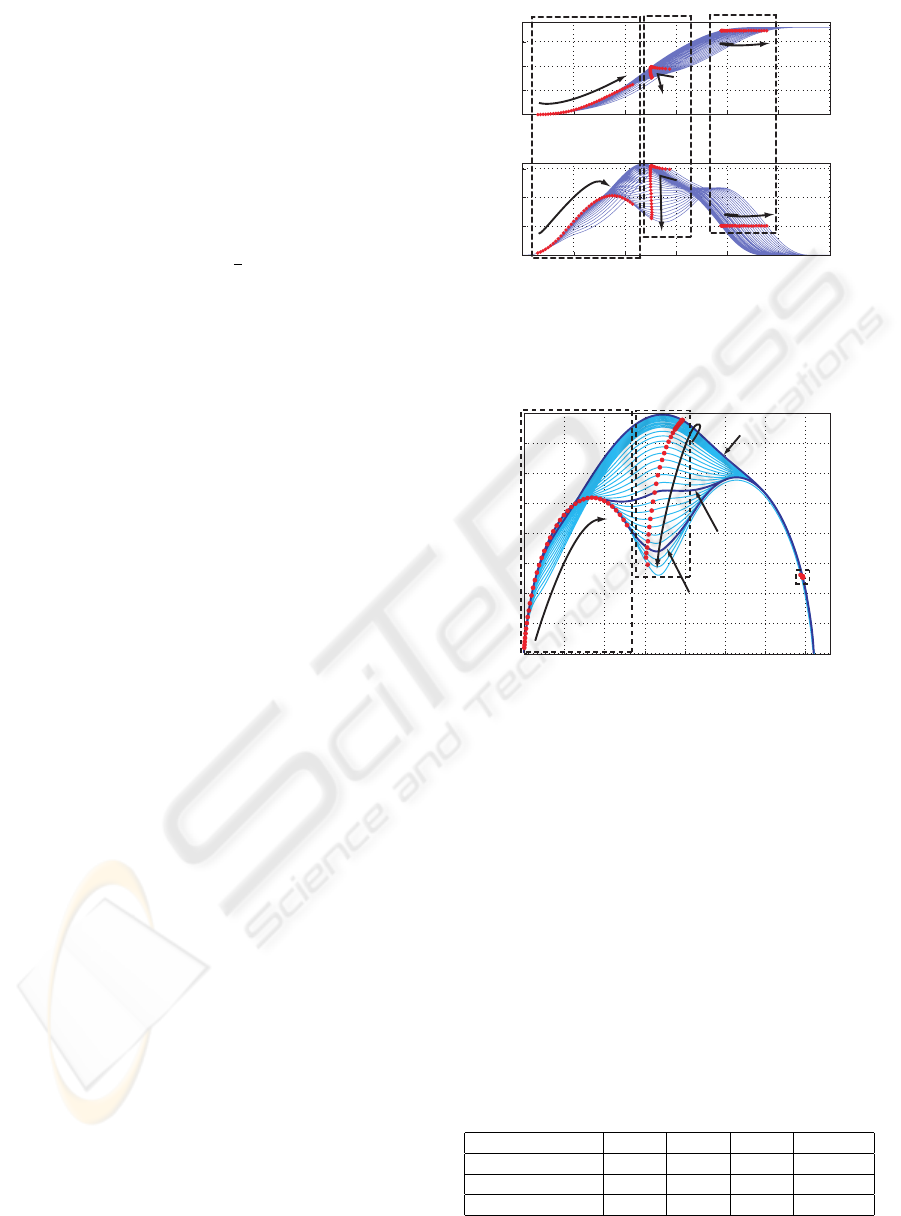
in a Simplex Method stated above are shown in
Figure 7 and Figure 8. Here, Figure 7 shows the
time response of rotor angle and angular velocity,
and Figure 8 shows the phase plane trajectory. The
point in the figure is control time of the pulse input,
and the arrows shows transitions of the pulse input
timing when T
1
changes from 300[µs] to 2200[µs].
VelocityErrorPlane method is commonly used in the
phase plane trajectory of the stepping motor to pre-
vent a transverse axis from becoming long (D.Ebihara
and T.Iwasa, 1984). Here, in VelocityErrorPlane
method, the phase difference
π
2
is subtracted when-
ever the excitation phase is switched. However, in this
paper, to see the response to control time of pulse four
times, the angle without subtracting the phase differ-
ence was drawn in a transverse axis.
There is a width of about 1[ms] to settling to the
desired angle using pulse timing in this study. Mo-
tion time can be shortened to use the pulse timing in
the trajectory with large angular velocity on the phase
plane.
When the current dynamics is not considered, the
changeover point on the phase plane without vibra-
tion by the desired angle is 3.6[deg] and 0[deg/s]
(D.Ebihara and T.Iwasa, 1984). However, it is con-
firmed that the last changeover point is the smaller
angle than 3.6 [deg], when there is the transient re-
sponse of the current. As seen from Figure 7, the time
to reach at the desired angle is about 700 [µs] after
the fourth input pulse is given, and it corresponds to
the transient response of the current for pulse input
assumed from Figure3. Consequently, it is confirmed
that the excitation sequence with a little vibration can
be obtained only by considering the response of the
current. Therefore, to realize the vibration-free re-
sponse in the full step drive, the proposed model con-
sidering the current dynamics and the control design
based on the model are made clear through these anal-
yses.
5 EXPERIMENTAL RESULTS
Three patterns are selected based on the timing de-
signed in Section 4 and experiments are done. The
pulse control time used in the experiments is shown
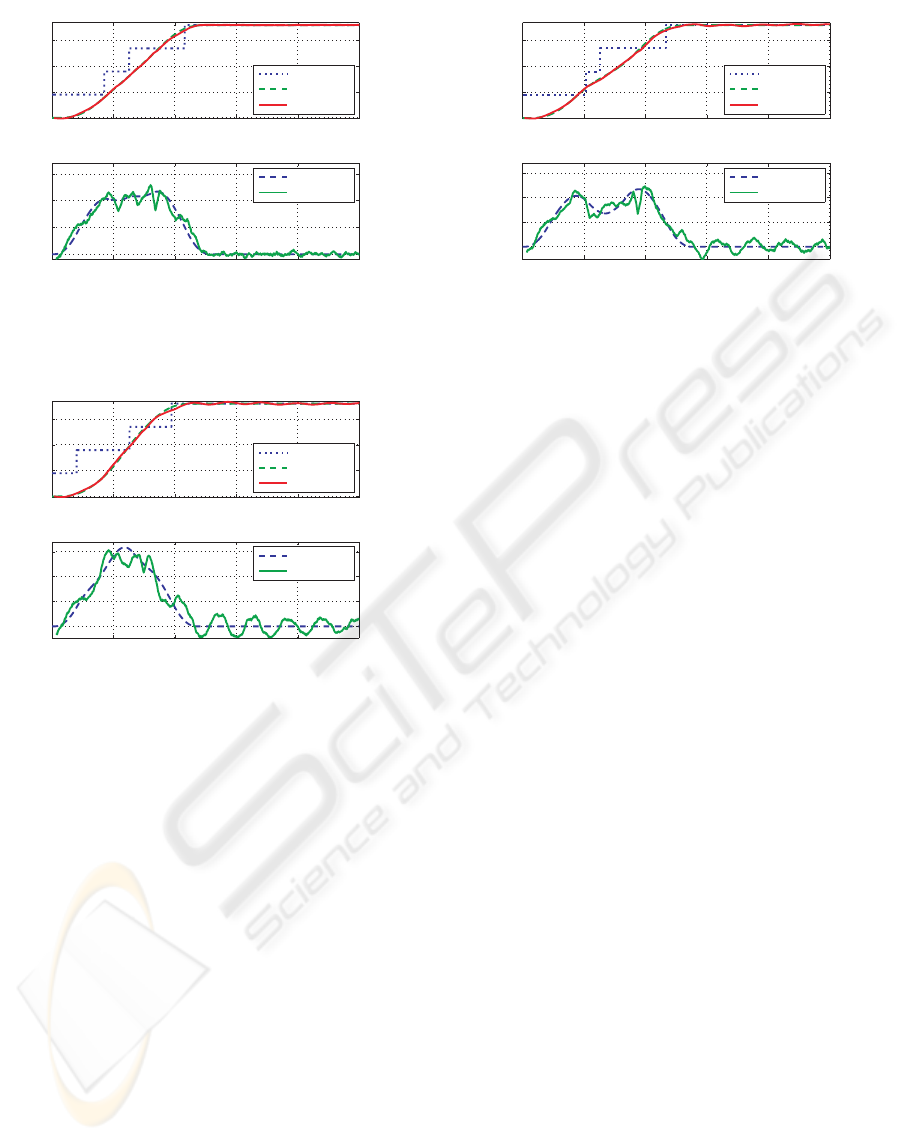
in Table 3. Experimental results of No.1, No.2, and
No.3 are shown in Figure 9, Figure 10, and Figure 11,
respectively.
Simulation results of both the angles and the an-
gular velocity corresponds well to experimental re-
sults. Especially, the vibration of experimental num-
ber No.1 was suppressed within 0.01 [deg] as the
same as resolution of encoder.
0 0.001 0.002 0.003 0.004 0.005 0.006
0
1
2
3
Time[s]
Angle[deg]
0 0.001 0.002 0.003 0.004 0.005 0.006
0
500
1000
1500
Time[s]
Angular velocity[deg/s]
2nd Pulse
3rd Pulse
4th Pulse
Figure 7: Simulation result of time response using 4 pulse
input of various control time.
0 0.5 1 1.5 2 2.5 3 3.5
0
200
400
600
800
1000
1200
1400
1600
Angle[deg]
Angular velocity[deg/s]
2nd Pulse
3rd Pulse
4th Pulse
Experiment No.2
Experiment No.1
Experiment No.3
Figure 8: Phase plane trajectory of stepping motor.
Moreover, a vibration of about 810[Hz] is con-
firmed that is higher than eigenfrequency of the motor
in Figure 10 and Figure 11. To realize more highly
accurate vibration suppression, it is necessary to con-
sider the vibration in the present model. It is thought
that this higher harmonic vibration is due to the influ-
ence of the harmonic component of the current, the
magnetic field of the drive circuit and the stepping
motor.
Through these results, the proposed model consid-
ering the response of the current enabled us to achieve
the pulse control with little vibration.
Table 3: Pulse timing.
Experiment No. T
1
[µs] T
2
[µs] T
3
[µs] Total[µs]
No.1 1700 810 1810 4320
No.2 800 1722 1368 3890
No.3 2050 476 2144 4670
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
392
0 0.002 0.004 0.006 0.008 0.01
0
1
2
3
Time[s]
Angle[deg]
0 0.002 0.004 0.006 0.008 0.01
0
500
1000
1500
Time[s]
Angular Velocity[deg/s]
Reference
Simulation
Experiment
Simulation
Experiment
Figure 9: Experimental result of case No.1.
0 0.002 0.004 0.006 0.008 0.01
0
1
2
3
Time[s]
Angle[deg]
0 0.002 0.004 0.006 0.008 0.01
0
500
1000
1500
Time[s]
Angular Velocity[deg/s]
Reference
Simulation
Experiment
Simulation
Experiment
Figure 10: Experimental result of case No.2.
6 CONCLUSIONS
In this paper, a mathematical model by means of the
torque equation of the stepping motor considering the
dynamics of the current has been built. The relation
between the response of the current and the excitation
timing on the phase plane were discussed for a full
step drive of four pulses. From the simulation, in the
system that there is the transient response in the cur-
rent, it was confirmed that the input timing of the last
pulse should be conducted before the end time, con-
sidering the duration time of current delay. The va-
lidity of the proposed model was shown by the com-
parison between the simulation and the experiment.
The pulse input timing without vibration was decided
by means of four pulses, and excellent vibration con-
trol was able to be realized based on the proposed
model using Simplex Method. The effectiveness of
the proposed approach was demonstrated through ex-
periments and simulations.
Robustness to the higher harmonic vibration and
0 0.002 0.004 0.006 0.008 0.01
0
1
2
3
Time[s]
Angle[deg]
0 0.002 0.004 0.006 0.008 0.01
0
500
1000
1500
Time[s]
Angular Velocity[deg/s]
Reference
Simulation
Experiment
Simulation
Experiment
Figure 11: Experimental result of case No.3.
model parameter variation by load variation, etc
should be investigated, and then robust control must
be achieved in near future.
REFERENCES
D.Ebihara and T.Iwasa (1984). Technology for Use of Step-
ping Motor in Japanese. Kogyo Chosakai Publishing
Co. Ltd.,, Tokyo.
F.Betin and D.Pinchon (1998). Robust speed control of a
stepping motor drive using fuzzy logic. In Proc IEEE
Int Conf Control Appl 1998 Vol.2 pp.948-952.
K.Laid, D.Xu, and J.Shi (2001). Vector control of hybrid
stepping motor position servosystem using neural net-
work control. In Annu Conf IEEE Ind Electron Soc
Vol.27 No.2 pp.1504-1508.
M.Bodson, J.N.Chiasson, R.T.Novotnak, and
R.B.Rekowski (1993). High-performance non-
linear feedback control of a permanent magnet
stepper motor. In IEEE Trans Control Syst Technol
Vol.1 No.1 pp.5-14.
M.Hamaguchi, K.Terashima, and H.Nomura (1994). Opti-
mal control of transferring a liquid container for sev-
eral performance specifications in japanese. In Trans
JSME Vol.60 No.573C pp.1668-1675.
S.M.Yang and E.L.Kuo (2003). Damping a hybrid stepping
motor with estimated position and velocity. In IEEE
Trans Power Electron Vol.18 No.3 pp.880-887.
T.Miura and T.Taniguchi (1999). Open-loop control of a
stepping motor using oscillation-suppressive exciting
sequence tuned by genetic algorithm. In IEEE Trans
Ind Electron Vol.46 No.6 pp.1192-1198.
T.Miura, T.Taniguchi, and H.Dohmeki (2000). Suppression
of rotor oscilation in microstepping of a stepping mo-
tor by pre-compensator in japanese. In T.IEE Japan
Vol.120-D No.12 pp.1462-1470.
MODELING WITH CURRENT DYNAMICS AND VIBRATION CONTROL OF TWO PHASE HYBRID STEPPING
MOTOR IN INTERMITTENT DRIVE
393
