A SPACE-EFFICIENT ALGORITHM FOR PAGING
UNBALANCED BINARY TREES
Rui A. E. Tavares and Elias P. Duarte Jr
Federal University of Paraná, Dept. Informatics, P.O. Box 19018, Curitiba, PR, Brazil
Keywords: Binary Trees, Paging, Bin Packing, Computational Biolog
y.
Abstract: This work presents a new approach for paging large unbalanced binar
y trees which frequently appear in
computational biology. The proposed algorithm aims at reducing the number of pages accessed for
searching, and at decreasing the amount of unused space in each page as well as reducing the total number
of pages required to store a tree. The algorithm builds the best possible paging when it is possible and
employs an efficient strategy based on bin packing for allocating trees that are not complete. The
complexity of the algorithm is presented. Experimental results are reported and compared with other
approaches, including balanced trees. The comparison shows that the proposed approach is the only one that
presents an average number of page accesses for searching close to the optimal and, at the same time, the
page filling percentage is also close to the optimal.
1 INTRODUCTION
Binary trees are data structures popular for allowing
efficient data searching (Gonnet and Baeza-Yates,
1991). A binary tree can get very large, and in this
case it may be impossible to keep the whole tree in
primary memory. A similar situation occurs when
the tree is stored remotely and is accessed through a
network. Many practical applications involve large
unbalanced trees, particularly computational
biology, in which trees are employed for string
processing (Cohen, 2004). Such trees are
constructed from biological sequences, which cannot
be messed with, i.e. these trees cannot be balanced,
so B-trees, for instance, cannot be employed
(Pedersen, 2000). In such cases, it is necessary to
define an efficient strategy to transfer the tree either
from secondary memory or from the remote
computer to primary memory where the search is
executed. Instead of transferring one data item at a
time, data collections called pages are usually
employed to improve the transfer latency.
As the time required to obtain a page is much
larger th
an the time required to process that page
once it is allocated in primary memory, the criteria
for allocating data in pages are essential for the
efficiency of executing search procedures. The
smallest the number of pages transferred, the fastest
the search procedure is executed.
This work presents a new algorithm for paging
binary trees. The algorithm
aims at reducing the
number of pages accessed for searching, and at the
same time decreasing the amount of unused space in
each page as well as reducing the total number of
pages required to store a tree. In this way, the
algorithm avoids wasting space to store a paged tree.
The algorithm obtains the best possible tree paging,
when it is possible, i.e. when the tree is complete
and information is not only stored at the leaves.
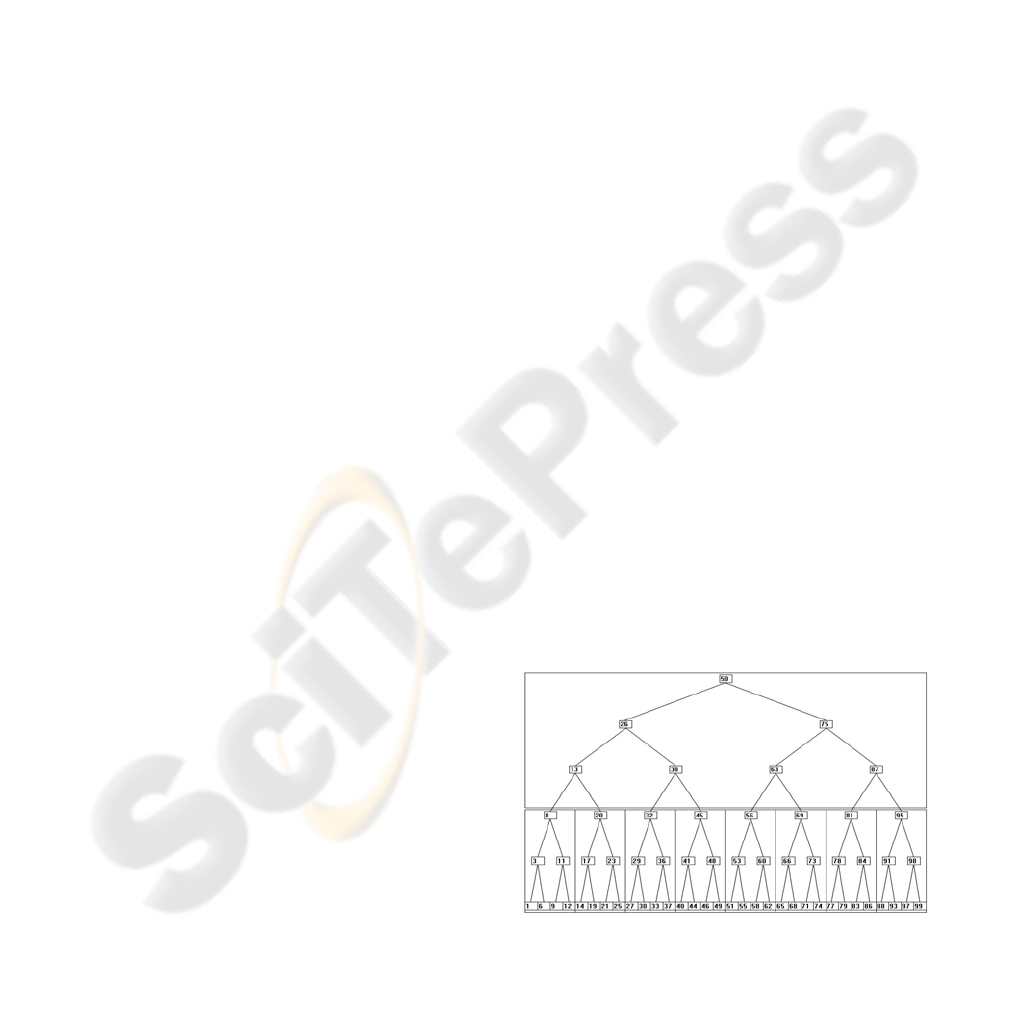
Figure 1 shows an example of the ideal paging for a
tree with 63 nodes grouped in pages of 7 nodes.
Besides that, an efficient strategy for allocating non-
complete trees based on bin packing (Garey and
Johnson, 1979) is presented.
Figure 1: The ideal tree paging.
The algorithm starts at the root of the tree to be
paged, allocating to the first page a subtree large
38
A. E. Tavares R. and P. Duarte Jr E. (2007).
A SPACE-EFFICIENT ALGORITHM FOR PAGING UNBALANCED BINARY TREES.
In Proceedings of the Second International Conference on Software and Data Technologies - PL/DPS/KE/WsMUSE, pages 38-43
Copyright
c
SciTePress
enough to completely fill the page. Next, every
subtree that completely fills a page is allocated to a
new page. The other subtrees that do not fill one
page completely are collectively called the fringe of
the tree. The algorithm allocates these subtrees in
pages using bin packing.
Packing, in this case, consists of the allocation of
a set of subtrees into a set of pages each with a
previously known amount of available space. The
number of pages required is minimized with this
strategy. Furthermore, each subtree is guaranteed to
be allocated in only one page, in order not to
increase the number of pages accessed for searching.
An alternative data structure used to organized
data in secondary memory is the B-tree (Gonnet and
Baeza-Yates, 1991). We show through experimental
results that our strategy is equivalent to B-trees in
terms of the average number of pages accesses for
searching. On the other hand our approach produces
a page filling percentage by more than 30% in
comparison with B-trees. Thus the total amount of
space required to transfer a tree from a remote site is
30% better when our approach is used, in
comparison with B-trees.
The rest of the paper is organized as follows. In
section 2 we give preliminary definitions. In section
3 the algorithm is described, its specification is
given as well as the complexity analysis. Section 4,
contains experimental results. Section 5 points to
related work, and section 6 concludes the paper.
2 PRELIMINARY DEFINITIONS
Binary trees are defined recursively as follows
(Gonnet and Baeza-Yates, 1991):
i) A binary tree T
0
of zero nodes is a binary tree.
ii) A binary tree T
n
of n > 1 nodes is a tuple (T
left
,
R, T
right
), where R is a single node called the root of
T
n
. T
left
and T
right
are binary trees, respectively called
left and right subtrees of the root. Considering that
T
left
has left nodes and T
right
has right nodes, then left
>= 0, right >= 0 and left + right = n − 1.
When it is not possible or desirable to keep the
whole tree in main memory, the tree nodes are
grouped in pages which are transferred to the main
memory one at a time. Each page is formed by cells,
each tree node is stored in a cell. As the time
required to process a page is mainly the time
required to transfer that page, the performance of
tree manipulation algorithms is strictly related to the
number of transferred pages.
Consider a binary tree with n nodes. Consider
that a page stores a maximum of p nodes. The
allocation of nodes to pages must be done so that
when a search algorithm or a tree traversal algorithm
are executed, the number of accessed pages is as
small as possible.
This work introduces a new algorithm for paging
binary trees. The algorithm initially allocates
subtrees which completely fill a page. The
remaining subtrees are collectively called the fringe
of the tree. The algorithm employs bin packing to
allocate the fringe to as small a number of pages as
possible, also keeping each subtree in only one page.
The bin packing problem is defined as follows.
Given a constant C and a finite list of items L = p
1
,
p
2
, ..., p
n
, where each item p, is associated to a w(p
i
)
value satisfying 0 < w(p
i
) < C, find the smallest
integer m such that L may be partitioned in m lists
L
1
, L
2
, ...,L
m
where each list L
i
, satisfies
∑
∈
≤=
ij
Lp
ji
CpwLw )()(
, i = 1,..,m.
In other words, the bin packing problem is
expected to partition of a list of items into sublists in
order to minimize the number of partitions
considering the capacity of each sublist.
In this work bin packing is employed to allocate
a set of subtrees to a set of pages. The algorithm
determines both the sizes of the subtrees to be
allocated, and the amount of space available in the
pages. The subtrees, with sizes s
1
, s
2
, ..., s
n
must be
allocated into C sized pages. By employing bin
packing, the algorithm obtains an allocation that
minimizes the number of pages required.
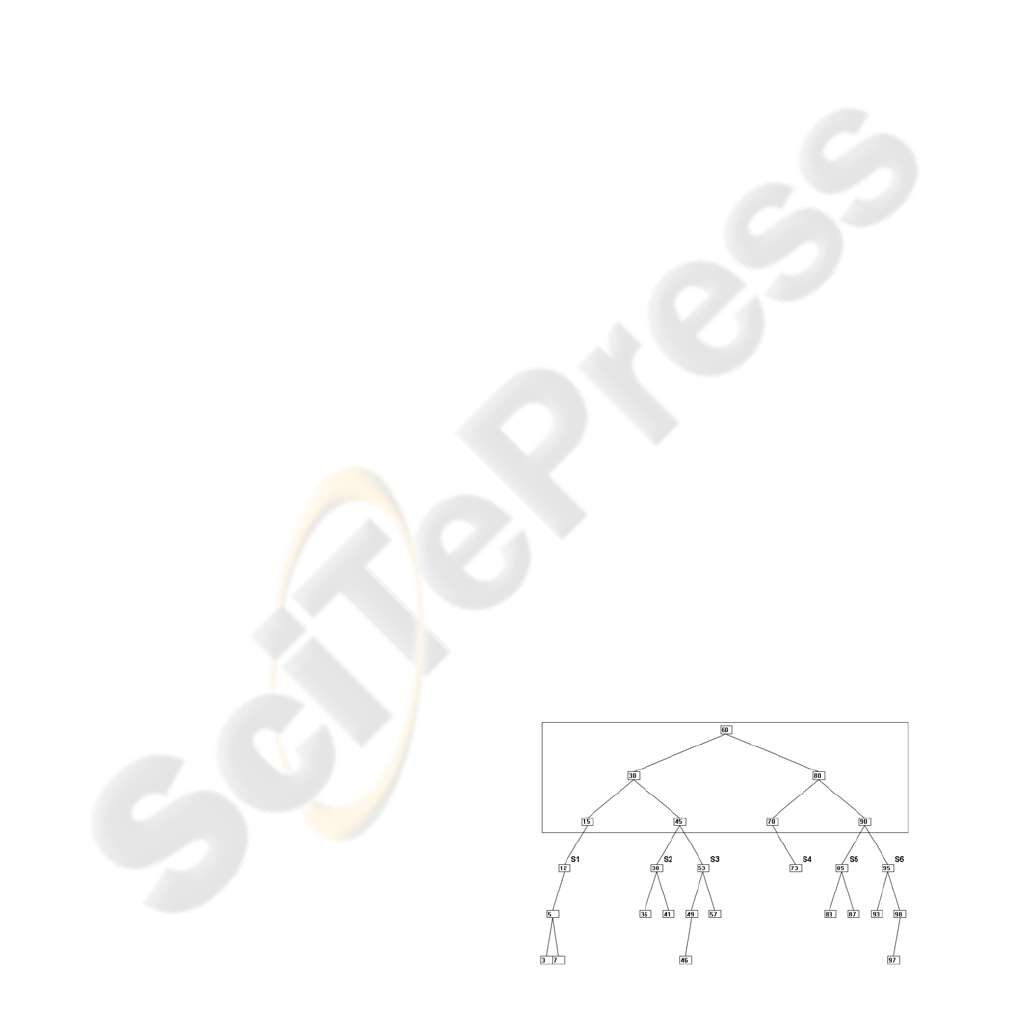
As an example, consider figure 2; subtree s
1
is
formed by nodes 3, 5, 7 and 12; s
2
is formed by
nodes 36, 38 and 41; s
3
is formed by nodes 46, 49,
53 and 57; s
4
is formed by node 73; s
5
is formed by
nodes 83, 85 and 87 and s
6
is formed by nodes 93,
95, 97 and 98. These subtrees must be allocated in
the smallest possible number of pages. So the sizes
of subtree’s are 4, 3, 4, 1, 3 and 4, respectively.
Consider that the page size is 7.
Figure 2: Bin packing: application example.
A SPACE-EFFICIENT ALGORITHM FOR PAGING UNBALANCED BINARY TREES
39
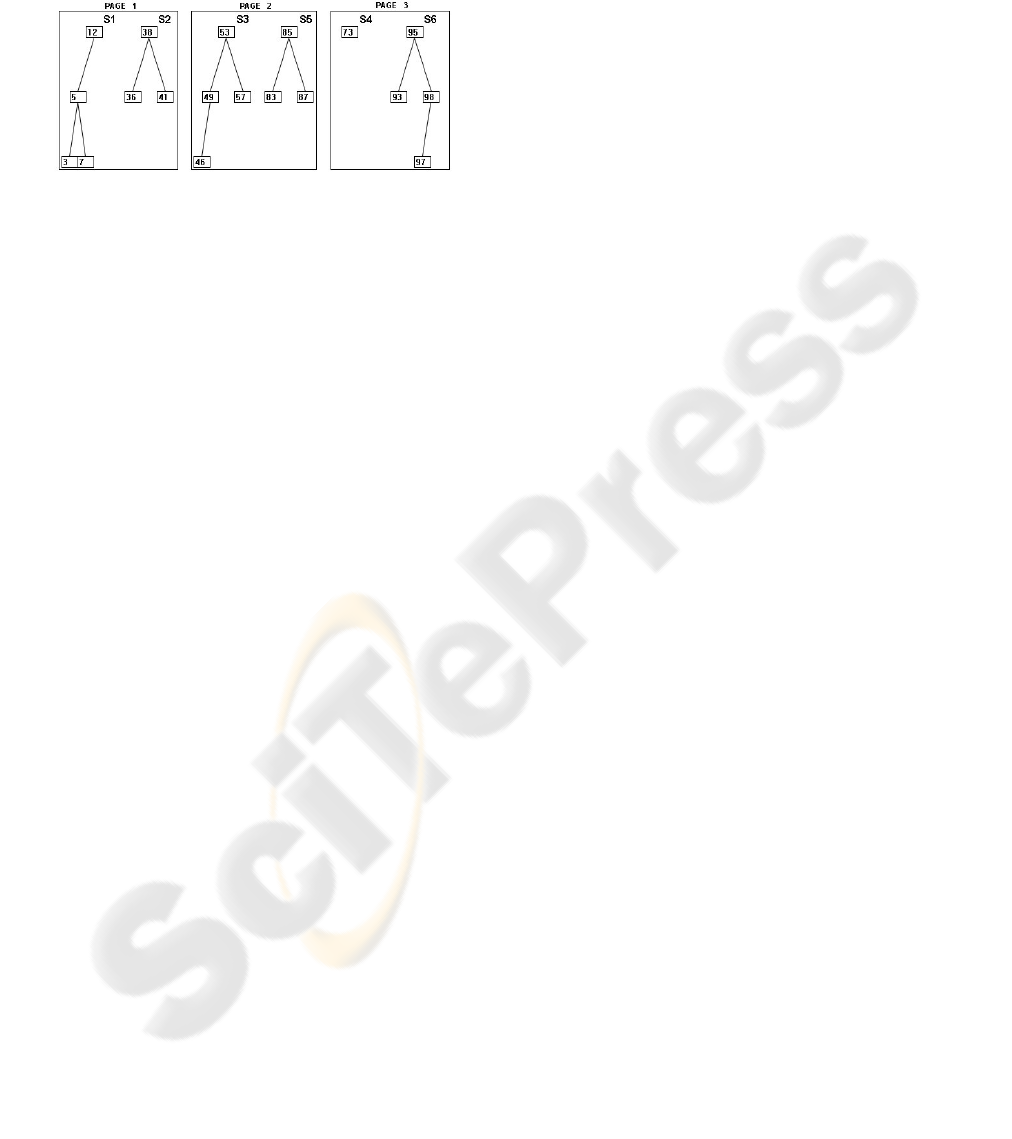
An optimal paging solution results in a high
filling page percentage, allocating subtrees s
1
and s
2
to page 1, subtrees s
3
and s
5
to page 2 and subtrees s
4
and s
6
to page 3, as illustrated on figure 3.
Figure 3: Paging by using bin packing.
The bin packing problem is a NP-hard
combinatorial optimization problem (Garey and
Johnson, 1979). Among the feasible alternatives for
bin packing implementation, several approximation
algorithms based on heuristics have been proposed
(Garey and Johnson, 1979). In those cases, there is
no guarantee that the optimal solution will be
obtained, but the execution time is polynomial. The
implementation used to obtain the experimental
results found in section 5 of this work is based on a
greedy approximation algorithm, that searches the
best allocation for each current page.
3 PRELIMINARY DEFINITIONS
This section presents the proposed algorithm for
paging binary trees. The algorithm can be applied
when the information set to be treated is static, the
access frequencies are not known and the storage is
remote or secondary.
3.1 Overview of the Algorithm
The proposed algorithm initially tries to group nodes
in pages such that the nodes in one page are as close
to each other as possible in the original tree. The
algorithm reaches the ideal paging when the binary
tree is complete and the number of nodes is a
multiple of the page size. Furthermore, it establishes
an efficient policy to page non-complete trees.
Before describing the algorithm, it is necessary
to give the definition of a patriarch. A patriarch is
the root of a subtree that is the first node of that
subtree to be allocated in a new page. As many
descendants of the patriarch as possible will be
allocated in that page. Consider that a page stores up
to x levels or generations of a tree, where x is a
positive integer, and the patriarch is at the first level.
The algorithm stores in one page 2
x
− 1 nodes.
The algorithm starts allocating the root of the
tree as the patriarch of the first page. The
descendants of the patriarch in the next x − 1 levels
are then allocated to the same page. At this point, if
unused space was left in this page, it is filled with
subtrees of the subsequent levels. If the page is
completely filled, a new patriarch is chosen for a
new page, and the process is repeated. If the subtrees
of the subsequent levels do not completely fill the
unused space, they belong to the fringe of the tree.
The algorithm later uses bin packing to allocate all
fringe subtrees.
3.2 Algorithm Specification
The proposed algorithm uses two data structures
called SQ (Stack-Queue) and FL (Fringe List). FL is
a linear list (Gonnet and Baeza-Yates, 1991) that
keeps the roots of the subtrees that belong to fringe.
SQ is a linear list SQ = (a
1
, a
2
, ..., a
n
) in which
insertions and removals are possible at one end,
called either rear or top, while at the other end,
called front, only removals can be executed. The
operations defined for SQ are the following:
create(SQ), initializes SQ as an empty data structure;
enqueue(x, SQ), inserts an element x at the rear of
SQ, returning the resulting structure; dequeue(SQ),
removes the element at the front end of SQ,
returning the element and the resulting structure;
pop(SQ), removes an element from the top of SQ,
returning the element and the resulting structure;
empty(SQ), returns true when SQ is empty and false
otherwise.
The algorithm is now described in terms of these
data structures. Initially, the root of the tree is
enqueued in SQ. The patriarch of a new page is
dequeued from SQ. The patriarch descendants in the
next x − 1 levels are then allocated to this page.
If the page is completely filled, every element of
the subsequent level is enqueued in SQ if it is the
root of a subtree that has size greater than of equal to
the page size; otherwise it is inserted in FL.
When a page is not completely filled, i.e. there is
available space, every element of the subsequent
level that is the root of a subtree that has size greater
than or equal to the available space in the current
page is enqueued in SQ; otherwise it is inserted in
FL.
The algorithm proceeds as follows. The last
element enqueued in SQ is popped and stored in the
page. Its sons are enqueued in SQ. If there is still
available space in the current page, and SQ is not
ICSOFT 2007 - International Conference on Software and Data Technologies
40

empty, again the last element enqueued in SQ is
popped and stored in the page, and its sons are
enqueued in SQ. This process is repeated until the
current page is completely filled or SQ is empty.
When the current page is completely filled, that
is, with no available space, the algorithm starts
filling a new page. The patriarch of this new page is
dequeued from SQ. The process above is repeated in
order to fill the page.
When SQ is empty, the algorithm starts to
allocate the fringe subtrees. The algorithm considers
both the sizes of these subtrees, the available space
in the last page, as well as the page size. The
algorithm employs bin packing to determine the
smallest number of pages that allocates those
subtrees.
The proposed algorithm is specified in high level
pseudocode in figure 4.
A Space-Efficient Algorithm for Paging
Binary Trees
Let the page size be 2**x-1
BEGIN
create(SQ);
enqueue(the tree root, SQ);
REPEAT
create a new page;
patriarch <- dequeue(SQ);
allocate to current page the patriarch and
its descendants of the next x-1 levels;
IF (the page is completely filled)
THEN
FOR-ALL nodes at the subsequent level
IF (node is root of subtree with size >=
page size)
THEN enqueue(node, SQ);
ELSE insert node in FL;
ELSE
/* there is space available in current page
*/
FOR-ALL nodes at the subsequent level
IF (node is root of subtree with size >=
available space)
THEN enqueue(node, SQ);
ELSE insert node in FL;
WHILE (there is available space in current
page)and (not empty(SQ)) DO
node <- pop(SQ);
allocate node to current page;
FOR-ALL sons of the allocated node
enqueue(son, SQ);
END-WHILE;
UNTIL empty(SQ);
IF (FL is not empty)
THEN
apply bin packing for paging the fringe
subtrees;
Figure 4: The proposed algorithm.
3.3 Algorithm Complexity
The complexity analysis is performed considering
the algorithm divided in two phases. The first phase
allocates the whole tree in pages, except the fringe.
The second phase allocates the fringe using bin
packing.
Let f be a worst-case complexity function, such
that f(n) is the largest number of node accesses that
the algorithm requires when the total number of
nodes is n.
The complexity of the algorithm’s first phase is
linear, actually 4n. Such linearity can be confirmed
as follows. To compute the number of descendants
of each node n accesses are required. To store all
nodes of the tree in pages, 2n accesses are required:
n accesses to allocate the nodes themselves and n
accesses to record the page address at the node’s
parent. Finally, at most n accesses are required in
order to insert and remove nodes from the data
structures employed, SQ and FL; less than n nodes
are ever inserted in one of these data structures. A
node that is inserted in one of them, is not inserted in
the other. Once a node is removed from the
structure, it is not inserted again.
The algorithm’s second phase depends mainly on
the bin packing algorithm employed. Consider g the
complexity of such algorithm, where g(n) describes
the number of node accesses required to allocate the
fringe subtrees. A number of practical
approximation algorithms with quadratic complexity
function are reported in the literature (Garey and
Johnson, 1979). In this case, the algorithm
complexity is quadratic.
4 EXPERIMENTAL RESULTS
This section presents experimental results. The
implementation used to obtain the experimental
results is based on a greedy approximation
algorithm, that searches the best allocation for each
current page. The metrics used to measure the
algorithm performance are described. Results are
compared to those of other approaches, including
sequential allocation, breadth-first allocation, depth-
first allocation, theoretical optimal paging of
balanced trees and B-trees.
Experiments were performed with random
sequences of keys. The trees had from 10 to 2000
nodes, in intervals of 10 nodes. The experiments
were divided according to the page size, considering
the values 3, 7 and 15. For each page size 100
experiments were performed.
A SPACE-EFFICIENT ALGORITHM FOR PAGING UNBALANCED BINARY TREES
41
4.1 Evaluation Metrics
To evaluate the proposed algorithm’s performance,
two metrics were defined: the amount of unused
space left in the pages, and the number of pages
accessed when searching is executed.
4.2 Evaluating the Number of Pages
Accessed for Searching
The first experiment reported refers to the total
number of pages accessed for searching all nodes.
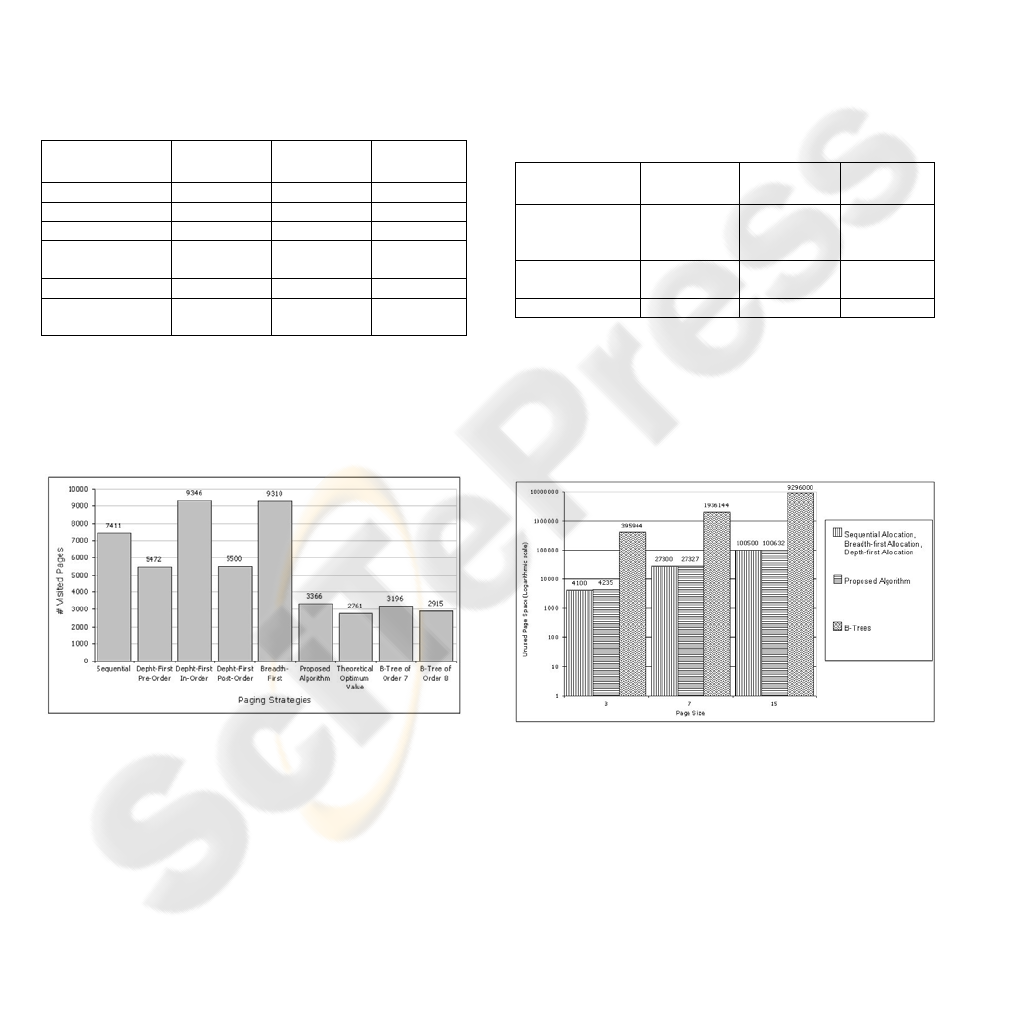
Table 1 shows the comparison.
Table 1: Average number of accessed pages in different
strategies.
Strategies
Page Size
= 3
Page Size
= 7
Page Size
= 15
Sequential 1495,99 3313,30 7410,69
Breadth-First 1681,04 3981,23 9309,85
Depth-First 1198,61 2500,61 5471,75
Proposed
Algorithm
969,69 1726,17 3365,44
B-trees 841,04 1644,62 2914,78
Theoretical
Optimum
771,45 1383,10 2760,65
Figure 5 presents the average number of
accessed pages considering page size equal to 15. As
shown in the figure, results were compared to those
produced by the usage of other approaches.
Figure 5: Average number of accessed pages; page size =
15.
Considering the presented results, the proposed
algorithm is always better than sequential, breadth-
first and depth-first allocation and worse than the
theoretical optimal value, being however much
closer to the optimal results than to others
approaches.
In comparison with B-trees, the number of pages
accessed for searching is similar. However, as
presented in the next subsection, the proposed
approach is much more efficient than B-trees in
terms of space efficiency.
4.3 Space-Efficiency Analysis
Another experimental result refers to the unused
space left in the pages. Table 2 shows the average
page filling percentage obtained in different
strategies.
In the performed experiments it was observed
that B-trees present a page filling percentage of
67.52% for randomized trees. On the other hand, the
proposed algorithm presents an average page filling
percentage of 98.62%, near to the optimal obtained
with sequential paging.
Table 2: Page filling percentage in different strategies.
Strategies
Page Size
= 3
Page Size
= 7
Page Size
= 15
Sequential,
Breadth-First,
Depth-First
98.82% 98.42% 98.69%
Proposed
Algorithm
98.77% 98.42% 98.68%
B-trees 67.15% 67.30% 67.75%
Figure 6 shows the total amount of unused space
produced by the different approaches. Considering
B-trees the total bandwidth required to transfer a
complete tree is proportionally larger than that
required to transfer a tree paged with the proposed
algorithm.
Figure 6: Amount of unused space measured
experimentally.
5 RELATED WORK
Many algorithms and data structures have been
proposed for treating massive data stored in external
memory (Frakes and Baeza-Yates, 1992; Baeza-
Yates and Ribeiro-Neto, 1999; Vitter, 2001),
including the allocation of trees. A technique for
allocating a binary tree partially paged using
ICSOFT 2007 - International Conference on Software and Data Technologies
42

external balancing is presented in (Henrich, SIX and
Widmayer, 1990). Algorithms for maintaining a
suffix tree structure in secondary storage are
presented in (Clark and Munro, 1996). A clustering
algorithm generating optimal worst-case external
path length mapping of tree structures is described in
(Diwan, Rane, Seshadri and Sudarshan, 1996). An
efficient dynamic programming algorithm to pack
trees is presented in (Gil and Itai, 1999). Another
approach to pack trees in hierarchical memory using
approximate algorithms is proposed in (Bender,
Demaine and Farach-Colton, 2002).
6 CONCLUSION
This work described an efficient algorithm for
paging unbalanced binary trees. The algorithm can
be particularly applied for computational biology, in
which large trees constructed from biological
sequence, that cannot be balanced, are frequently
found. The algorithm obtains the best possible
allocation of nodes to pages when it is possible and
proposes an efficient policy for filling pages of non-
complete trees, based on the application of bin
packing to the fringe of the tree. The complexity of
the algorithm is given, which depends on the
packing algorithm’s complexity. The algorithm was
implemented and experimental results were
presented.
Considering the average number of accessed
pages per search, the algorithm produces a page
allocation up to 55% better than sequential
allocation, up to 64% better than breadth-first and
depth-first allocation, and results that are very close
to those obtained with B-trees. On the other hand,
considering the amount of unused space per page,
and the total number of pages required, the
algorithm presents an average page filling
percentage of 98.62%. The comparison shows that
the proposed approach is the only one that presents
an average number of page accesses for searching
close to the optimal and, at the same time, the page
filling percentage is also close to the optimal.
Future work includes investigating
experimentally the behavior of the algorithm
considering other approximation algorithms for
packing the fringe, and comparing those results to
those obtained with variations of B-trees. Another
topic left as future work is the evaluation of the
behavior of the algorithm considering dynamic data,
with frequent insertions and removals of nodes, as
well as the impact of concurrent data access. The
evaluation of the algorithm considering real data
instead of random data is also left as future work.
REFERENCES
Gonnet, G. H. ; Baeza-Yates, R. Handbook of Algorithms
and Data Structures: in Pascal and C. Addison-
Wesley, 1991, 424 p.
Cohen, J. Bioinformatics - An Introduction for Computer
Scientists. ACM Computing Surveys, v. 36, n. 2, p.
122-158, 2004.
Pedersen, C. N. S. Algorithms in Computational Biology.
PhD Dissertation, University of Aarhus, Denmark,
2000, 210 p.
Garey, M. R. ; Johnson, D. S. Computers and
Intractability: A Guide to the Theory of NP-
Completeness. W. H. Freeman and Company, 1979,
338 p.
Frakes, W. B. ; Baeza-Yates, R. Information Retrieval
Data Structures and Algorithms. Prentice Hall, 1992,
464 p.
Baeza-Yates, R. ; Ribeiro-Neto, B. Modern Information
Retrieval. Addison-Wesley, 1999, 513 p.
Vitter, J. S. External Memory Algorithms and Data
Structures: Dealing with Massive Data. ACM
Computing Surveys, v. 33, n. 2, p. 209-271, 2001.
Henrich, A. ; SIX, H.W. ; Widmayer, P. Paging Binary
Trees with External Balancing. Proceedings of the
15th International Workshop on Graph-theoretic
Concepts in Computer Science, p. 260-276,
Netherlands, 1990.
Clark, D. R. ; Munro, J. I. Efficient Suffix Trees on
Secondary Storage. Proceedings of the 7th Annual
ACM-SIAM Symposium on Discrete Algorithms, p.
383-391, Atlanta, 1996.
Diwan, A. A. ; Rane, S. ; Seshadri, S. ; Sudarshan, S.
Clustering Techniques for Minimizing External Path
Length. Proceedings of the 22nd VLDB Conference,
p. 342-353, India, 1996.
Gil, J. ; Itai, A. How to Pack Trees. Journal of Algorithms,
v. 32, n. 2, p. 108-132, 1999.
Bender, M. A. ; Demaine, E. D. ; Farach-Colton, M.
Efficient Tree Layout in a Multilevel Memory
Hierarchy. Proceedings of the 10th Annual European
Symposium on Algorithms, p. 165-173, Italy, 2002.
A SPACE-EFFICIENT ALGORITHM FOR PAGING UNBALANCED BINARY TREES
43
