SCUBA DIVER: SUBSPACE CLUSTERING
OF WEB SEARCH RESULTS
Fatih Gelgi, Srinivas Vadrevu and Hasan Davulcu
Department of Computer Science and Engineering, Arizona State University, Tempe, AZ, U.S.A.
Keywords:
Web search, subspace clustering, guided search.
Abstract:
Current search engines present their search results as a ranked list of Web pages. However, as the number of
pages on the Web increases exponentially, so does the number of search results for any given query. We present
a novel subspace clustering based algorithm to organize keyword search results by simultaneously clustering
and identifying distinguishing terms for each cluster. Our system, named Scuba Diver, enables users to better
interpret the coverage of millions of search results and to refine their search queries through a keyword guided
interface. We present experimental results illustrating the effectiveness of our algorithm by measuring purity,
entropy and F-measure of generated clusters based on Open Directory Project (ODP).
1 INTRODUCTION
Current search engines present their search results as
an ordered list of Web pages ranked in terms of their
relevance to the user’s keyword query. As the number
of pages on the Web is increasing exponentially, the
number of search results for any given query is also
increasing at the same rate. For example there are 544
million results returned by Google search engine
1
for
the keyword query ‘apple’. Therefore even though
there are millions of potentially relevant documents
for any given user’s query and interest, only top few
ranking documents in the first few pages of a search
engine results can be found and explored.
An alternate way to browse the search results re-
turned by a search engine is to organize them into re-
lated clusters to guide the user in her search. When
the search results are clustered and organized in terms
of their distinguishing features, it may become easier
for users (i) to interpret the coverage of millions of
search results and (ii) to refine their search queries.
Traditionally, clustering has been applied to Web
pages in the context of document clustering such as
Clusty
2
and Mooter
3
. They have fair performance
and cluster descriptions are not identified in these sys-
1
http://www.google.com
2
http://www.clusty.com
3
http://www.mooter.com
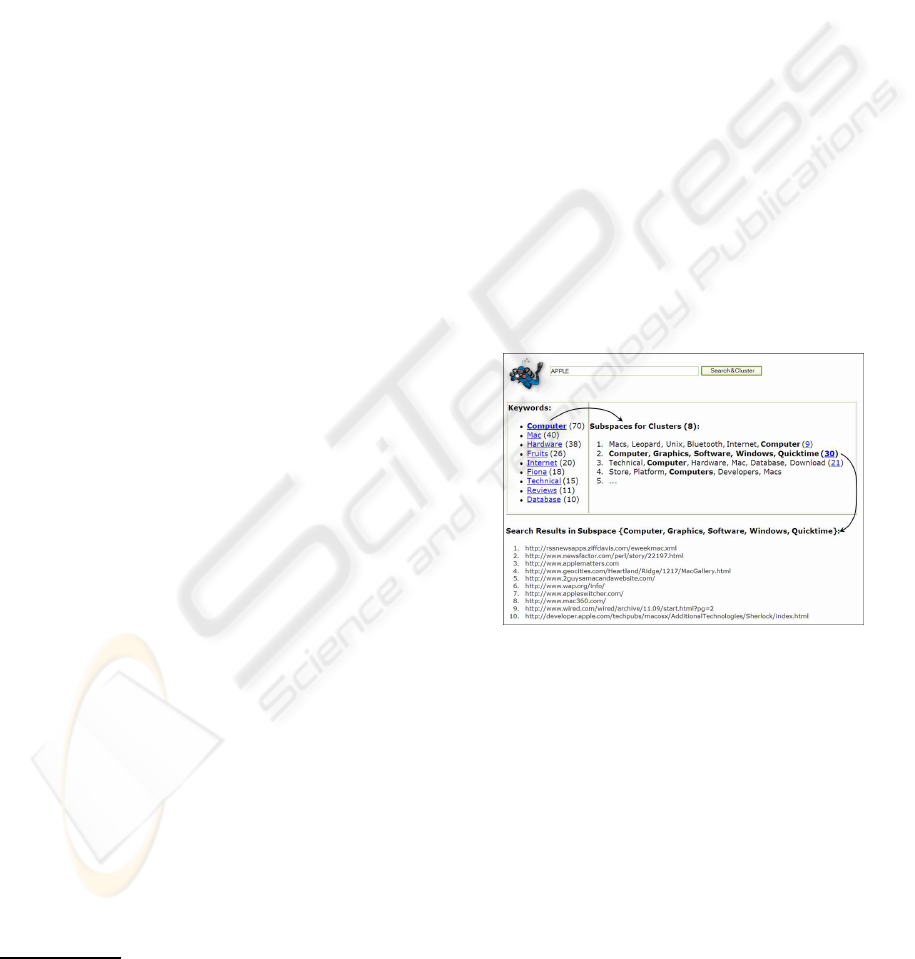
Figure 1: Clustered results for keyword query ‘apple’.
tems. (Crescenzi et al., 2005) utilizes the structure
of HTML pages to cluster them. They utilize lay-
out and presentation properties of blocks of similarly
presented links in identifying clusters of Web pages.
Their clustering algorithm is based on the observation
that similar pages share the same layout and presenta-
tion structures.
In this paper, we present a way to organize the
search results by clustering them into groups of Web
pages that belong to the same category. Subspace
clustering (Parsons et al., 2004) is an extension of tra-
ditional clustering that seeks to find clusters in dif-
ferent subspaces of feature space within a data set.
We choose subspace clustering since it provides the
distinguishing features that make up each cluster, in
334
Gelgi F., Vadrevu S. and Davulcu H. (2007).
SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS.
In Proceedings of the Third International Conference on Web Information Systems and Technologies - Web Interfaces and Applications, pages 334-339
DOI: 10.5220/0001288503340339
Copyright
c
SciTePress

addition to clustering the documents. These features
can be used as additional guidance information in or-
ganizing the search results.
Figure 1 illustrates the keyword query ‘apple’ and
the clusters of Web pages along with their subspace
labels. We refine the clusters obtained by subspace
clustering by merging similar clusters and partition-
ing them so that each Web page belongs to only one
cluster. The figure also shows the related keywords
comprising all labels, ordered in terms of their occur-
rence frequency. These keywords provide an addi-
tional way to filter and navigate through the search re-
sults. Figure 1 shows top four clusters along and their
subspaces for the keyword query ‘apple’ after filter-
ing the subspaces with the keyword ‘computer’ from
the related keywords area. The individual results of
any matching cluster can be displayed by clicking on
the corresponding subspace.
Related work includes clustering techniques have
been used previously in the area of information re-
trieval to organize the search results. (Zeng et al.,
2004) models the search result clustering problem as
ranking salient phrases extracted from the search re-
sults. The phrases (cluster names) are ranked by us-
ing a regression model with features extracted from
the title and snippets of search results. (Beil et al.,
2002) works on frequent-term based text clustering.
One of their data set is collected from Yahoo! subject
hierarchy classified into 20 categories with 1560 Web
pages. Their best F-measure is 43% for the Web data
which is substantially low compared with their exper-
iments on text documents. Other researchers (Leouski
and Croft, 1996; Leuski and Allan, 2000) utilize tra-
ditional machine learning based clustering algorithms
to cluster the search results and choose descriptive
cluster names from various frequency based features
of the documents.
The rest of the paper is organized as follows.
Problem description and formalization is given in
Section 2. Details of our algorithm is presented in
Section 3 and the experiments is presented in Section
4. We conclude and give the future work in Section 5.
2 PROBLEM DESCRIPTION
In large datasets such as Web, clustering algorithms
have to deal with two challenges as indicated in
(Agarwal et al., 2006): (i) sparsity – the data is sparse
if most of the entries of vectors are zero, (ii) high-
dimensional data – the number of features in dataset
is large. In the Web domain, we have both problems
since the features are terms in the domain, and a Web
page is related with a very small fragment of this term
set. Classical clustering techniques use feature trans-
formation and feature selection to overcome the de-
scribed problems above. On the other hand, newer
techniques such as subspace clustering (Parsons et al.,
2004) localizes its search and is able to identify clus-
ters that exist in multiple, possibly overlapping sub-
spaces instead of examining the dataset as a whole.
Subspace clustering also uncovers the relevant fea-
tures of the clusters and keeps the original ones that
make the interpretation easier.
Context can be defined as the subset of terms in
the domain. Hence one can consider context as the
subspace of the Web pages in the same cluster. In
our formalization, F refers to the feature set selected
from all the terms in the collection of Web pages.
Definition 1 (Subspace Cluster) A subspace cluster
is a cluster C = hf, wi composed of a pair of sets
where f ⊆ F is the feature set (or the subspace) of
the cluster and w ⊆ W is the set of Web pages be-
longing to the cluster. We denote f (C) and w(C) as
the features and Web pages of a cluster respectively.
Formal definition of our problem can be stated as:
Problem statement 1 Given a set of Web pages
W = {W
1
, W
2
, . . . W
n
} resulting from an ambigu-
ous keyword search K, find the clusters of Web pages
together with their descriptive terms. A Web page W
i
is defined as the set of the its terms.
This problem can be reduced a subspace cluster-
ing problem as follows:
Problem statement 2 Given a binary n × m ma-
trix M , where rows represent n Web pages (W =
{D
1
, D
2
, . . . D
n
}) and columns represent m terms
(F = {t
1
, t
2
, . . . t
m
}), find subspace clusters of Web
pages, W ⊆ W defined in the subspace of terms,
T ⊆ F.
Here D
i
= hd
i1
, d
i2
, . . . d
im
i represents the bi-
nary vector of the Web page W
i
where d
ij
= 1 when
t
j
∈ W
i
. In the matrix M, d
ij
correspond to the entry
in the i
th
row and j
th
column, that is M
ij
= d
ij
.
3 SCUBA DIVER ALGORITHM
Our subspace clustering algorithm given in Algo-
rithm 1 is composed of three steps: feature selection,
subspace clustering, and merging and partitioning.
3.1 Feature Selection
This step is given the first line in ScubaDiver func-
tion (ScubaDiver refers to the main function of the
algorithm) in Algorithm 1. SelectF eatures function
SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS
335

Algorithm 1 Clustering of Web Search Results
ScubaDiver(W, K)
Input: K, the search keyword; W, a set Web pages resulting from keyword
search K
Output: C, set of subspace clusters of the Web pages W
1: F ← SelectF eatures(
S
W ∈W
W )
2: for ∀W
i
∈ W
3: for ∀t
j
∈ F
4: if t
j
∈ W
i
then M
ij
← 1
5: else M
ij
← 0
6: C ← SCuBA(M, α, β)
7: C ← M erge(C, δ, ξ)
8: C ← P artition(W, C)
9: return C
End of ScubaDiver
Merge(C, δ, ξ)
Input: C, subspace clusters; δ, threshold for the common features; ξ,
threshold for the common Web pages;
Output: C, set of merged subspace clusters of the Web pages W
1: for ∀C
i
∈ C
2: for ∀C
j
∈ (C − {C
i
})
3: if (Jaccard(f(C
i
), f(C
j
)) > δ)∧
4: (Jaccard(w(C
i
), w(C
j
)) > ξ) then
5: C
′
← hf (C
i
) ∪ f (C
j
), w(C
i
) ∪ w(C
j
)i
6: C ← C − {C
i
, C
j
} ∪ {C
′
}
7: return C
End of Merge
P artition(W, C)
Input: W, set of Web pages; C, subspace clusters;
Output: C, set of partitioned subspace clusters of the Web pages W
1: for ∀W
i
∈ W
2: closest ← arg max
C
j
∈C
{similarity(v(C
j
), v(W
i
))}
3: w(closest) ← w(closest) ∪ {W
i
}
4: C
′
← {X|X ∈ (C − {closest}) ∧ W
i
∈ w(X)}
5: for ∀C
j
∈ C
′
6: w(C
j
) ← w(C
j
) − {W
i
}
7: return C
End of Partition
selects features for clustering among all the terms ap-
peared in the data.
In SelectF eatures function, data has first been
preprocessed then features have been selected by
three common frequency based methods in Informa-
tion Retrieval (IR). Term frequency of a term t is,
T F (t) =
n
t
P
k∈F
n
k
where n
t
is the number of occur-
rences of t in the domain. Document frequency of t is,
DF (t) =
|D(t)|
n
where D(t) is the set of Web pages
t appears. A common variation of Term frequency /
inverse document frequency of t is, T F/IDF (t) =
T F (t). lg
1
DF (t)
. Readers should note that deep anal-
ysis of feature selection is out of scope of this paper.
Based on the three measures abovethe features are
selected as top-m ranked terms among all the terms
in the data excluding the search keyword K. For ex-
ample, top-10 TF/IDF terms obtained from the Web
pages with the search keyword apple in our experi-
ments are ‘mac’, ‘recipe’, ‘ipod’, ‘search’, ‘software’,
‘computer’, ‘macintosh’, ‘list’, ‘store’ and ‘pie’.
3.2 Subspace Clustering
Due to its efficiency and effectiveness on binary data,
we use the subspace clustering algorithm SCuBA de-
scribed in (Agarwal et al., 2006) which is part of an
article recommendationsystem for researchers. In Al-
gorithm 1, lines from 2 to 5 prepare the binary matrix
M for SCuBA and line 6 generates the subspace clus-
ters. SCuBA works in two steps: (i) it compacts the
data by reducing the n × m matrix to n rows each of
which is a list of the size of its corresponding Web
page, and (ii) it searches for the subspaces by com-
paring each row to the successive rows to find the in-
tersecting rows and their subsets of columns.
SCuBA produces many small subspace clus-
ters with many overlapping Web pages. Exam-
ple of two subspace clusters generated from apple
search have {macintosh, computer, imac, mac}
and {macintosh, check, mac} as their feature sets
containing 4 Web pages each, 2 of which are com-
mon.
3.3 Merging and Partitioning
Final clusters are determined after merging step as the
post-processing on subspace clusters in lines 7 and 8
in Algorithm 1. In the Web data subspace clusters
obtained from SCuBA are in the form of sub-matrices
which are not significant in number and size. Clusters
needs to be relaxed to have irregular shapes and to
cover more data as opposed to strict sub-matrices.
A common scenario is the overlapping subspace
clusters which are the subsets of the same actual clus-
ter and the context. Hence it is reasonable to merge
the subspace clusters C
i
and C
j
if they share certain
amount of terms and Web pages. Jaccard similarity
coefficient is one of the common measure for com-
paring the similarity and diversity of the sets. The
Jaccard coefficient is defined as the size of the inter-
section divided by the size of the union of the sets,
Jaccard(X, Y ) =
|X∩Y |
|X∪Y |
.
In Algorithm 1, M erge function merges the sub-
space clusters by adopting the Jaccard coefficient to
measure the similarity of the set of features and Web
pages of two clusters. If the similarity is more than the
thresholds δ and ξ respectively, we merge the clusters.
Formally, in lines 3-6 if Jaccard(f(C
i
), f(C
j
)) > δ
WEBIST 2007 - International Conference on Web Information Systems and Technologies
336
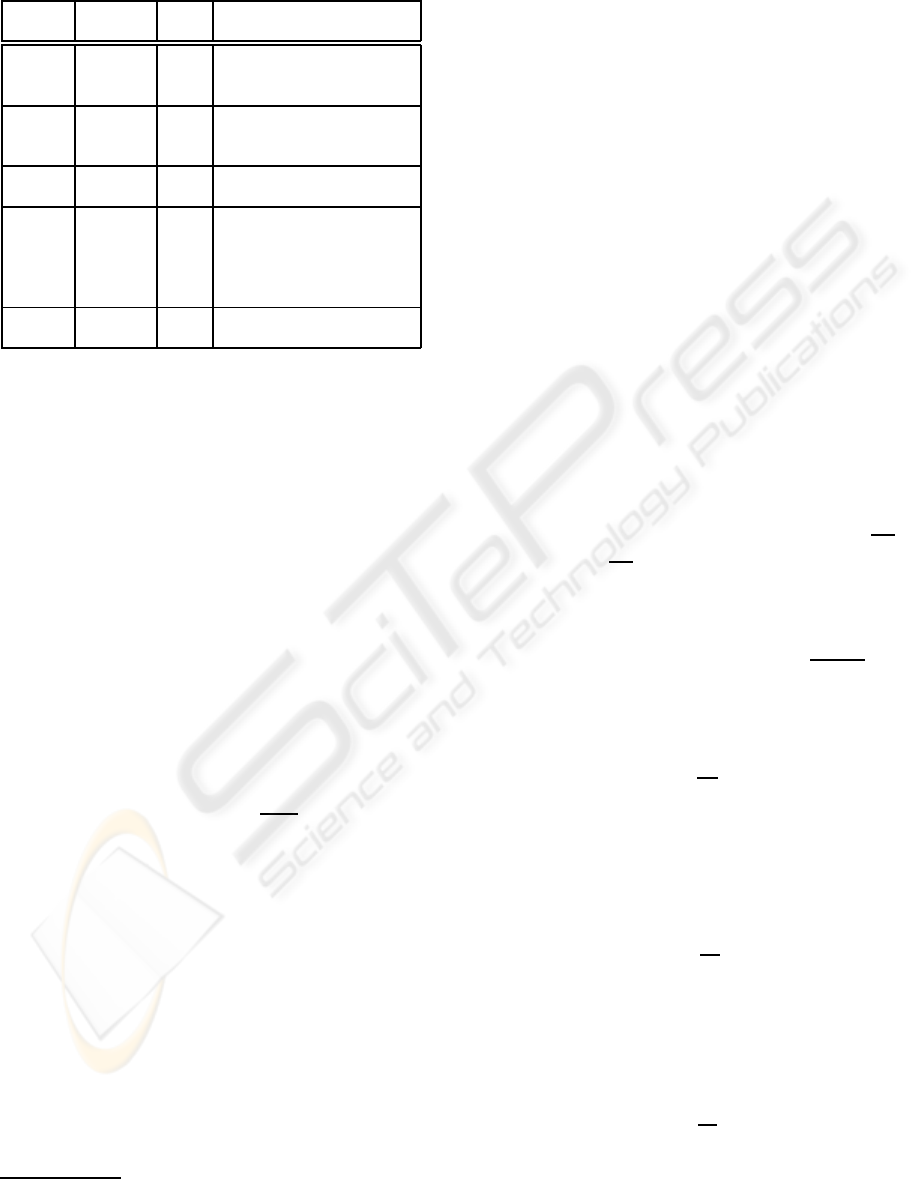
Table 1: Selected search keywords and their corresponding
categories in data sets.
Keyword # of # of Categories
categories pages
apple 6 648 Computers(463), Fruits(136),
Locations(17), Music(21),
Movies(6), Games(5)
gold 6 670 Shopping(471), Mining(151),
Movies(28), Motors(11),
Games(8), Sports(1)
jaguar 4 138 Cars(78), Video games(48),
Animals(9), Music(3)
paper 10 1422 Shopping(626), Materials(380),
Academic(113), Arts(107),
Money(78), Games(39),
Computers(27), Consultants(23),
Environment(19), Movies(10)
saturn 4 71 Cars(22), Planets(21),
Anime(19), Video games(9)
and Jaccard(w(C
i
), w(C
j
)) > ξ, the merged cluster
C
′
becomes C
′
= hf(C
i
) ∪ f (C
j
), w(C
i
) ∪ w(C
j
)i .
Following the same example given in Section
3.2, the two subspace clusters C
i
and C
j
is merged
due to the high overlap in their features and Web
pages. Their Jaccard coefficients for the features and
Web pages are Jaccard(f(C
i
), f(C
j
)) = 0.4 and
Jaccard(w(C
i
), w(C
j
)) = 0.33.
Note that subspace clustering is a soft clustering
method that allows a Web page to be in multiple cate-
gories. This flexibility is more realistic for real world
data. Besides, hard clustering is also possible. A sim-
ple idea is to assign each Web page to its closest sub-
space cluster and eliminate the duplicates from other
clusters. In the P artition function in Algorithm 1,
line 2 calculates the closest cluster for each Web page
W
i
. Here v(·) returns the feature vector. Subspace
cluster vector can be considered as the feature vector
of that cluster, and cosine measure can be used for the
similarity, similarity(x, y) =
x•y
|x||y|
where x and y
are the vectors of the cluster and the Web page.
Cosine is determined as one of the best measures
for Web page clustering, and also for binary and
sparse data (Strehl et al., 2000). Lines 4-6 remove
the duplicates from other clusters. All the remaining
Web pages which doesn’t belong to any cluster are put
in one cluster called ‘others’.
4 EXPERIMENTS
In our experiments, we identified some challenging
keywords inspired from (Zeng et al., 2004) on Open
Directory Project
4
(ODP).
4
http://www.dmoz.org
We used the search keywords ‘apple’, ‘gold’,
‘jaguar’, ‘paper’ and ‘saturn’ for data collection. For
each search keyword we prepared the data from the
resulting Web pages as givenin Table 1. In the prepro-
cessing step, the common data types of values such
as percentage, dates, numbers etc., stop words, and
punctuation symbols are filtered using simple regular
expressions to standardize the data.
In each keyword data, the features are selected as
top-1000 terms which are ranked based on TF/IDF
measure as mentioned in Section 3.1. We consider
1000 terms are sufficiently enough to capture the con-
textual information given in the Web pages. Discus-
sions on feature selection are given in Section 4.2.
Subspace clusters are required to have at least 3
features and 3 Web pages for the thresholds α and
β. For merging subspaces, the thresholds δ and ξ are
determined as 0.2 and 0.1 respectively.
4.1 Evaluation Metrics
To evaluate the quality of our results, the clusters are
compared with the actual categories given in ODP.
We use the common evaluation metrics in cluster-
ing (Rosell et al., 2004) such as precision, recall, F-
measure, purity, and entropy. Precision, p
ij
=
n
ij
n
i
and recall, r
ij
=
n
ij
n
j
compare each cluster i with each
category j where n
ij
is the number of Web pages ap-
pear in both the cluster i and the category j, n
i
and n
j
are the number of Web pages in the cluster i and in the
category j respectively. F-measure, F
ij
=
2p
ij
r
ij
p
ij
+r
ij
is a
common metric calculated similarly to the one in IR.
The F-measure of a category j is F
j
= max
i
{F
ij
}
and similarly the overall F-measure is:
F =
X
j
n
j
n
F
j
. (1)
Quality of each cluster can be calculated by purity
and entropy. Purity measures how pure is the clus-
ter i by ρ
i
= max
j
{p
ij
}. The purity of the entire
clustering can be calculated by weighting each clus-
ter proportional to its size as:
ρ =
X
i
n
i
n
ρ
i
(2)
where n is the total number of Web pages.
The entropy of a cluster i is E
i
=
−
P
j
p
ij
log p
ij
. Calculating the weighted av-
erage over all clusters gives the entire entropy of the
clustering:
E =
X
i
n
i
n
E
i
. (3)
Note that for soft clustering, n in Equations 2 and
3 has to be the sum of the sizes of the clusters since
SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS
337
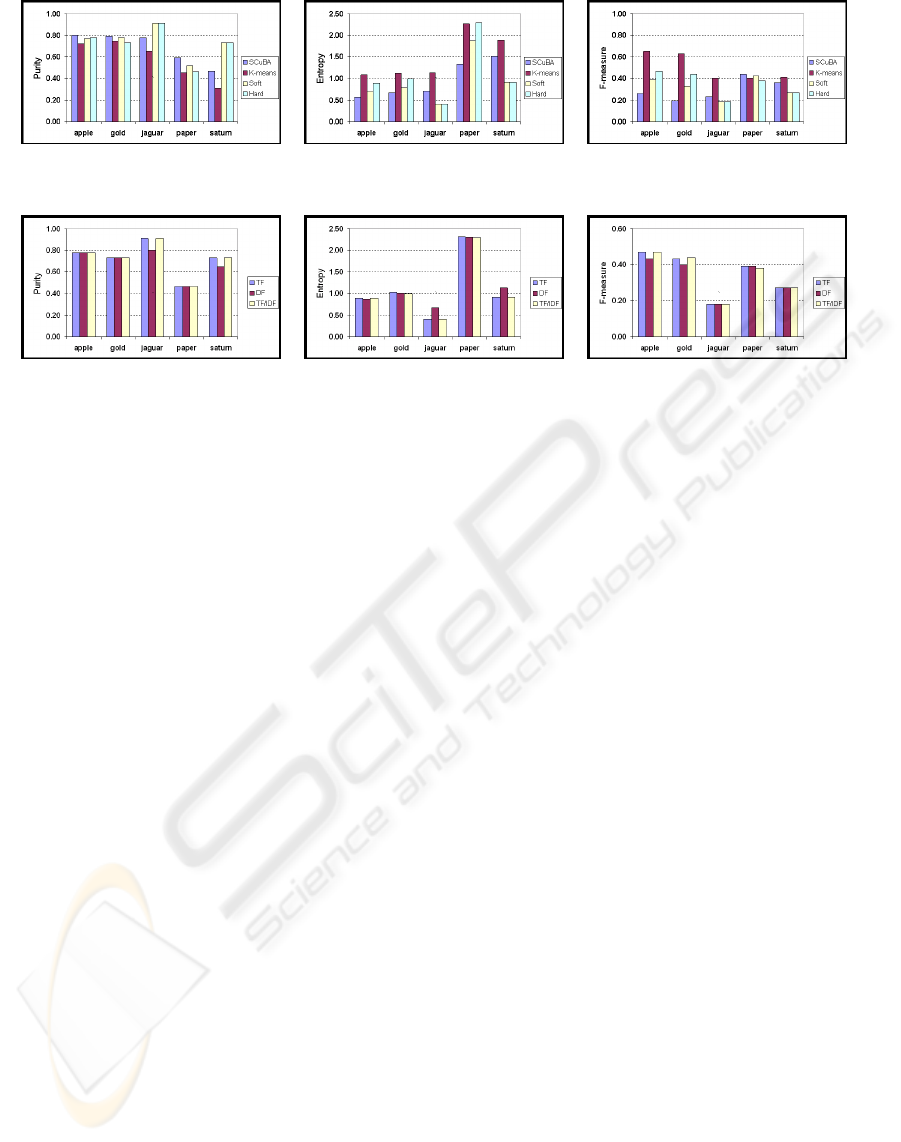
(a) (b) (c)
Figure 2: Comparison of clustering methods.
(a) (b) (c)
Figure 3: Effect of the future selection methods.
a Web page might appear in more than one clusters.
F-measure is related with the size of categories hence
n remains the same in Equation 1.
4.2 ODP Results
First we use a wrapper which sends the given search
keyword to http://www.dmoz.org, and collects
the resulting categories and the Web pages belong to
those categories. Collected pages are categorized by
their main ODP categories. Next, all the text is ex-
tracted from the collected Web pages.
K-means clustering method is used as a baseline
measure to demonstrate to quality of our method. K-
means is one of the common clustering methods pre-
ferred for its speed and quality. In our experiments,
even K is provided which is a great advantage for K-
means over our method. For each keyword data, K-
means has been executed 20 times and the results are
the average of all runs. Purity, entropy and F-measure
are deviated in the interval of ±0.05.
Figure 2 and Table 2 presents the performance of
the subspace clustering vs. the baseline method, K-
means. SCuBA refers to the initial subspace clusters
generated by SCuBA algorithm, Soft refers the soft
clusters after merging the subspace clusters, and Hard
refers to the final hard clusters after partitioning.
As shown in Figure 2(a) and (b), our method sur-
passes K-means in purity and entropy measures sig-
nificantly although the number of clusters are pro-
vided to K-means. SCuBA generates small but pure
subspace clusters. However, F-measure is low due to
the excessive number of clusters, and there are too
many redundant clusters with many duplicate pages
as shown in Table 3. Although sensitive and ag-
gressive merging in our method reduces the number
of clusters substantially and increases the F-measure,
there are still too many clusters and duplicates in soft
clustering, and F-measure is not comparable with K-
means. In addition, F-measure is especially low in
jaguar and saturn data since they don’t have rich
subspaces that prevents to identify common subspace
clusters to merge.
Features of some of the subspace clusters are pre-
sented in Table 4. One can notice the common terms
such as ‘contact’, ‘privacy’, and ‘see’ in paper data
that lead the worst quality among the other keywords.
Merging due to the common terms degenerates the
purity of the clusters as opposed to F-measure. An-
other reason for the purity to be low in paper data is
its context ambiguity; the context of categories have
more overlaps than the other keywords have. For in-
stance, many Web pages in Shopping, Materials, Arts,
and Money have content about the quality of papers.
Determining the number of clusters has been a
challenging problem for clustering methods. As
shown in Table 3, our algorithm generated more clus-
ters than the actual for apple and gold keywords.
Sometimes main clusters can not be generated due
to the completely separate context in subcategories.
For example, hardware and software subcategories
are identified however they are not clustered together.
Clusters are less in paper data due to the merging
caused by common terms in the data.
Top-1000 terms are sufficient to include all the de-
scriptive and discriminative terms in the collections.
However, they also contain common and ambiguous
terms which hinders clustering process such as ‘e-
mail’,‘forum’, and ‘contact’.
TF, DF and TF/IDF measures have not affected
WEBIST 2007 - International Conference on Web Information Systems and Technologies
338

Table 2: Performance comparison of clustering methods. P, E and F refers to purity, entropy and F-measure respectively.
SCuBA Soft K-means Hard
Keyword P E F P E F P E F P E F
apple 0.80 0.57 0.26 0.77 0.70 0.39 0.72 1.08 0.65 0.78 0.89 0.47
gold 0.79 0.67 0.19 0.78 0.78 0.33 0.75 1.11 0.63 0.73 0.99 0.44
jaguar 0.78 0.71 0.23 0.91 0.40 0.18 0.65 1.12 0.40 0.91 0.40 0.18
paper 0.59 1.34 0.44 0.52 1.87 0.42 0.45 2.27 0.40 0.46 2.29 0.38
saturn 0.47 1.52 0.36 0.73 0.91 0.27 0.31 1.89 0.41 0.73 0.91 0.27
Table 3: Comparison of actual clusters with clustering methods. Clusters and Pages refers to number of clusters and number
of total Web pages in the clusters respectively.
# of # of SCuBA Soft K-means Hard
Keyword Cat. pages Clusters Pages Clusters Pages Clusters Clusters
apple 6 648 801 4402 181 2406 6 23
gold 6 670 578 3276 165 2077 6 27
jaguar 4 138 15 88 4 95 4 4
paper 10 1422 2054 12593 120 3516 10 6
saturn 4 71 12 86 3 66 4 3
Table 4: Sample features of one subspace cluster for each
keyword.
Keyword Sample features Related Category
apple macintosh, users, computer, Computers
product, check, imac, mac
gold necklace, ring, pendant, earring Shopping
bracelet, shipping, silver, jewelry
jaguar auto, cars, parts, support Cars
paper printing, contact, privacy, product, Shopping
unique, see
saturn planet, sun, image, satellite Planets
the performance of subspace clustering significantly
as shown in Figure 3. Especially, TF and TF/IDF
showed nearly the same performance. As opposed
to the expectations, although the common terms are
ranked in lower, it is surprising to find out TF/IDF is
not able to eliminate them.
Consequently, our subspace clustering based algo-
rithm preserves the quality of the clusters initially ob-
tained from SCuBA while significantly reducing the
number of clusters. Furthermore, it is better than a
common state of art clustering algorithm although the
number of clusters are provided.
5 CONCLUSION
We present a novel subspace clustering based algo-
rithm to organize search results by simultaneously
clustering and identifying their distinguishing terms.
We present experimental results illustrating the effec-
tiveness of our algorithm by measuring purity, en-
tropy and F-measure of generated clusters based on
Open Directory Project (ODP). As the future work,
we will work on feature selection to eliminate com-
mon terms to increase the quality of the features.
Currently, merging is a simple rule based method,
whereas one can explore the use of sophisticated rela-
tionship analysis over clusters.
REFERENCES
Agarwal, N., Haque, E., Liu, H., and Parsons, L. (2006).
A subspace clustering framework for research group
collaboration. International Journal of Information
Technology and Web Engineering, 1(1):35–38.
Beil, F., Ester, M., and Xu, X. (2002). Frequent term-based
text clustering. In Proceedings of SIGKDD’02, pages
436–442, New York, NY, USA. ACM Press.
Crescenzi, V., Merialdo, P., and Missier, P. (2005). Clus-
tering web pages based on their structure. Data and
Knowledge Engineering, 54:279–299.
Leouski, A. and Croft, W. B. (1996). An evaluation of tech-
niques for clustering search results. Technical Report
IR-76, University of Massachusetts, Amherst.
Leuski, A. and Allan, J. (2000). Improving interactive re-
trieval by combining ranked lists and clustering. In
Proceedings of RIAO’2000, pages 665–681.
Parsons, L., Haque, E., and Liu, H. (2004). Subspace clus-
tering for high dimensional data: A review. SIGKDD
Explorations, 6(1):90.
Rosell, M., Kann, V., and Litton, J.-E. (2004). Compar-
ing comparisons: Document clustering evaluation us-
ing two manual classifications. In Proceedings of
ICON’04.
Strehl, A., Ghosh, J., and Mooney, R. (2000). Impact of
similarity measures on web-page clustering. In Pro-
ceedings of AAAI’00, pages 58–64. AAAI.
Zeng, H.-J., He, Q.-C., Chen, Z., Ma, W.-Y., and Ma, J.
(2004). Learning to cluster web search results. In
Proceedings of ACM SIGIR’04, pages 210–217, New
York, NY, USA. ACM Press.
SCUBA DIVER: SUBSPACE CLUSTERING OF WEB SEARCH RESULTS
339
