
INCLUSION OF TIME-VARYING MEASURES IN TEMPORAL DATA
WAREHOUSES
Elzbieta Malinowski
∗
and E. Zim
´
anyi
Department of Informatics & Networks,Universit
´
e Libre de Bruxelles
50 av.F.D.Roosevelt, 1050 Brussels, Belgium
Keywords:
Temporal data warehouses, time-varying measures, data warehouse design.
Abstract:
Data Warehouses (DWs) integrate data from different source systems that may have temporal support. How-
ever, current DWs only allow to track changes for measures indicating the time when a specific measure value
is valid. In this way, applications such as fraud detection cannot be easily implemented since they require to
know the time when changes in source systems have occurred. In this work, based on the research related
to Temporal Databases, we propose the inclusion of time-varying measures changing the current role of the
time dimension. First, we refer to different temporal types that are allowed in our model. Then, we study
different scenarios that show the usefulness of inclusion of different temporal types. Further, since measures
can be aggregated before being inserted into DWs, we discuss the issues related to different time granularities
between source systems and DWs and to measure aggregations.
1 INTRODUCTION
Data warehouses (DWs) store and provide access
to large volumes of historical data supporting the
decision-making process. The structure of DWs is
based on a multidimensional view of data usually rep-
resented as a star schema, consisting of fact and di-
mension tables. A fact table contains numeric data
called measures. Dimensions are used for exploring
the measures from different analysis perspectives.
Current multidimensional models include an om-
nipresent time dimension that serves as a time-
varying indicator for measures, e.g., total sales in
March 2005; however, this dimension cannot be used
for representing the time when changes in other di-
mensions have occurred, e.g., when a product has
changed its ingredients. Therefore, usual multidi-
mensional models are not symmetric in representing
changes for measures and dimensions.
On the other hand, Temporal Databases (TDBs) al-
low to represent and manage time-varying informa-
tion. Two different temporal types
2
are considered:
∗
The work of E. Malinowski was funded by a scholar-
ship of the Cooperation Department of the Universit
´
e Libre
de Bruxelles.
2
Usually called time dimensions; however, we use the
term “dimension” in the multidimensional context.
valid time (VT) and transaction time (TT) that al-
low to know, respectively, when the data is true in
the modeled reality and current in the database. If
both temporal types are used, they define bitemporal
time (BT). These temporal types are used for repre-
senting events, i.e., something that happens at a par-
ticular time point, or states, i.e., something that has
extent over time. For the former an instant is used; it
is represented as a non-decomposable time unit called
granule with the size called granularity. A state is
represented by an interval or period indicating the
time between two instants.
Temporal Data Warehouses (TDWs) join the re-
search achievements of TDBs and DWs in order to
manage time-varying multidimensional data. TDWs
raise several issues, e.g., consistent temporal aggre-
gations, storage methods, etc. However, very little
attention has been drawn to conceptual modeling for
TDWs and to the analysis of which temporal support
should be included in TDWs considering that TDBs
and DWs are semantically different.
Firstly, DW data is integrated from existing source
systems whereas TDB data is inserted by users. Sec-
ondly, DW data is neither modified nor deleted
3
while
TDB data can be changed by users directly. Finally,
3
We ignore modifications due to errors during data load-
ing and deletion for purging DW data.
181
Malinowski E. and Zimányi E. (2006).
INCLUSION OF TIME-VARYING MEASURES IN TEMPORAL DATA WAREHOUSES.
In Proceedings of the Eighth International Conference on Enterprise Information Systems - DISI, pages 181-186
DOI: 10.5220/0002454301810186
Copyright
c
SciTePress

DWs are designed according to users’ analysis needs
based on the multidimensional model where measures
and dimensions play different roles. TDB design is
concerned with transactional applications where all
data is handled in a similar manner.
In this paper, we introduce temporal extensions for
the MultiDimER model (Malinowski and Zim
´
anyi,
2005). Due to space limitations, we only refer to
measures
4
. Section 2 briefly recalls the main fea-
tures of the MultiDimER model and Section 3 de-
scribes temporal types allowed in the model. Fur-
ther, since source systems and DWs may have differ-
ent time granularities
5
, e.g., source data is introduced
on a daily basis yet DW data is aggregated by month,
we consider two different situations: when measures
are not aggregated before integration into a TDW and
when these aggregations are realized. We refer to
the former in Section 4 presenting several scenarios,
for which different temporal types are required. Sec-
tion 5 considers the latter and refers to the mapping
between different time granularities and to aggrega-
tion of measures. Finally, Section 6 surveys works
related to TDWs and Section 7 gives the conclusions.
2 OVERVIEW OF THE
MULTIDIMER MODEL
In the MultiDimER model (Malinowski and Zim
´
anyi,
2005) a schema is defined as a finite set of dimensions
and fact relationships. A dimension is an abstract con-
cept for grouping data that shares a common semantic
meaning. It represents either a level, or one or more
hierarchies. Levels correspond to entity types (Fig-
ure 1 a). Every instance of a level is called a member.
A hierarchy contains several related levels (Fig-
ure 1 b). It express different structures according to
the criteria used for analysis (Figure 1 c), e.g., geo-
graphical location. Cardinalities (Figure 1 d) indicate
the minimum and the maximum numbers of members
in one level that can be related to a member in another
level. Given two consecutive levels of a hierarchy,
the higher level is called parent and the lower level is
called child. A level of a hierarchy that does not have
a child level is called leaf.
Levels contain one or several key attributes (repre-
sented in bold and italic in Figure 1) and may also
have other descriptive attributes. A key attribute of a
parent level defines how child members are grouped.
A key attribute in a leaf level or in a level forming a
dimension without hierarchy indicates the granularity
4
In (Malinowski and Zim
´
anyi, 2006) time-varying di-
mensions have been introduced.
5
We consider the granularity as a time precision in
which measure values are recorded.
Key attribute
Other attributes
Level name
a)
(1,N)
b)
c)
(0,N)
(1,1)
(0,1)
Criterion
d)
Key attribute
Other attributes
Level name
1
Fact
relationship
name
Measure attributes
e)
Key attribute
Other attributes
Level name
2
Figure 1: Notations for multidimensional model: a) one-
level dimension, b) hierarchy, c) analysis criterion, d) cardi-
nalities, and e) fact relationship.
of measures in the associated fact relationship.
A fact relationship (Figure 1 e) represents an n-
ary relationship between leaf levels. It may contain
attributes commonly called measures.
3 TEMPORAL TYPES IN TDWs
Current DWs do not offer different temporal types,
thus users may have difficulties in expressing their
needs for some kinds of applications, e.g., for fraud
detection. In the temporal extension of the Multi-
DimER model we allow to include VT, TT, or bitem-
poral time (BT) coming from source systems and ad-
ditionally, the time when data is loaded into a TDW.
The inclusion of VT for representing when the data
is valid in the modeled reality is important for TDW
applications since it allows to aggregate measures cor-
rectly (Eder et al., 2002).
Regarding TT, three different approaches exist: (1)
ignoring TT (Body et al., 2003; Mendelzon and Vais-
man, 2003), (2) transforming TT from source systems
to represent VT (Mart
´
ın and Abell
´
o, 2003), or (3) con-
sidering TT generated in a TDW in the same way as
TT is used in TDBs (Mart
´
ın and Abell
´
o, 2003; Kon-
cilia, 2003), i.e., allowing to know when data was in-
serted, modified, or deleted from DWs. However, us-
ing the first approach traceability applications, e.g.,
for fraud detection, cannot be implemented. The sec-
ond approach is semantically incorrect because data
may be included in databases after their period of va-
lidity has expired, e.g., client’s previous address. In
the third approach, since TDW data is neither modi-
fied nor deleted, TT generated in a TDW represents
indeed the time when data was loaded into a TDW.
This time is called in our model data warehouse load-
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
182
ing time (DWLT).
Further, in the modeling process, application re-
quirements determine the type of temporal support
needed in each element of a TDW (attributes, levels,
measures, etc.). Obviously that depends on whether
or not the different data sources of the TDW provide
temporal support. For example, snapshot systems
(Jarke et al., 2003), which in order to find the changes
require to compare data with the previous versions,
do not offer any temporal support except VT that may
be included as a user-defined attribute. On the other
hand, logged systems (Jarke et al., 2003), which reg-
ister all actions in the log files, contain TT; they also
may include VT similar to snapshot systems.
4 TEMPORAL SUPPORT FOR
NON-AGGREGATED
MEASURES
In this section we refer to the case when time gran-
ularities attached to measures in source systems and
in a TDW are the same, i.e., measures are not aggre-
gated. Considering that temporal support in TDWs
depends on both the availability of temporal types in
source systems and the kind of required analysis, we
present next examples that refer to these two aspects.
Case 1. Sources: non-temporal, TDWs: DWLT
In real-world situations, many sources can be non-
temporal or temporal support is implemented in an
ad-hoc manner that can be both inefficient and dif-
ficult to automate. Nevertheless, decision-making
users may require the history of how source data has
evolved (Yang and Widom, 1998). Thus, the measure
values can be timestamped when loaded to the TDW.
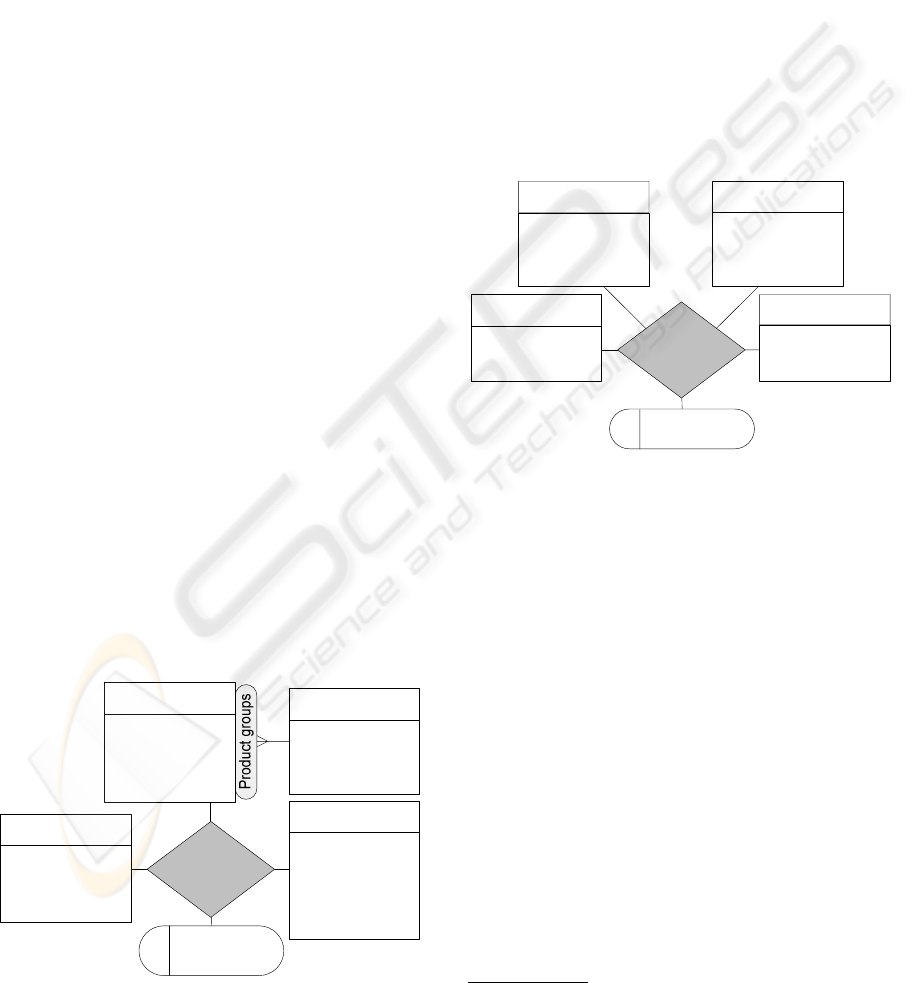
An example is given in in Figure 2 representing the
schema for analysis of the history of Product inven-
tory considering different suppliers and warehouses.
Inventory
Quantity
Cost
DW
LT
Supplier
Supplier id
Supplier name
Supplier address
Other attributes
Warehouse
WH number
WH name
WH address
City name
State name
Other attributes
Product
Product number
Product name
Description
Size
Other attributes
Category
Category name
Description
Responsible
Max amount
Figure 2: Inclusion of DWLT for measures.
The important question is whether it is necessary to
have the time dimension in the model after including
temporal types for measures. If the time dimension
has only the attributes that contain a granule, this di-
mension is not required anymore. The additional in-
formation, e.g., if it is the week day, the last day of the
month, can be obtained applying time manipulation
functions. However, in some TDW applications this
calculation can be very time-consuming or some data
cannot be acquired at all, e.g., occurred events
6
. Thus,
whether this dimension will be included depends on
users’ requirements and the DBMS capabilities.
Case 2. Sources and TDWs: VT This case occurs
when source systems can offer VT, which is also re-
quired in a TDW. Figure 3 gives an example of an
event model used for the analysis of banking transac-
tions. Different types of queries can be formulated for
Transactions
Amount
VT
Bank entity
Entity id
Entity name
Entity address
Other attributes
Client
Client id
Client name
Client address
Other attributes
Transaction type
Id
Name
Other attributes
Account
Account No.
Account type
Other attributes
Figure 3: Inclusion of VT for measures.
this model. For example, analysis of clients’ behavior
considering the maximum or minimum withdraw, the
total number of transactions during lunch hours, etc.
This can help, for example, to avoid cancellation of
an account or to promote some new services.
Case 3. Sources: TT, TDWs: VT In this case, users
require to know either the time when an event oc-
curred in reality or a period of validity for data repre-
senting state. However, source systems can only offer
the time when data was modified in a source system,
i.e., TT. Thus, the analysis if TT can be used for ap-
proximating VT should be made. For example, if a
measure represents clients’ account balance, VT for
this measure can be calculated considering transac-
tion times of two consecutive operations.
Nevertheless, TT cannot always be used for calcu-
lating VT, since some data can be inserted in source
systems (registering TT) when they are not valid in
the modeled reality, e.g., employee’s previous salary.
In many applications, only the user knows VT.
6
In Costa Rica when an event such as earthquake occurs,
sales of water bottles and canned food increases.
INCLUSION OF TIME-VARYING MEASURES IN TEMPORAL DATA WAREHOUSES
183
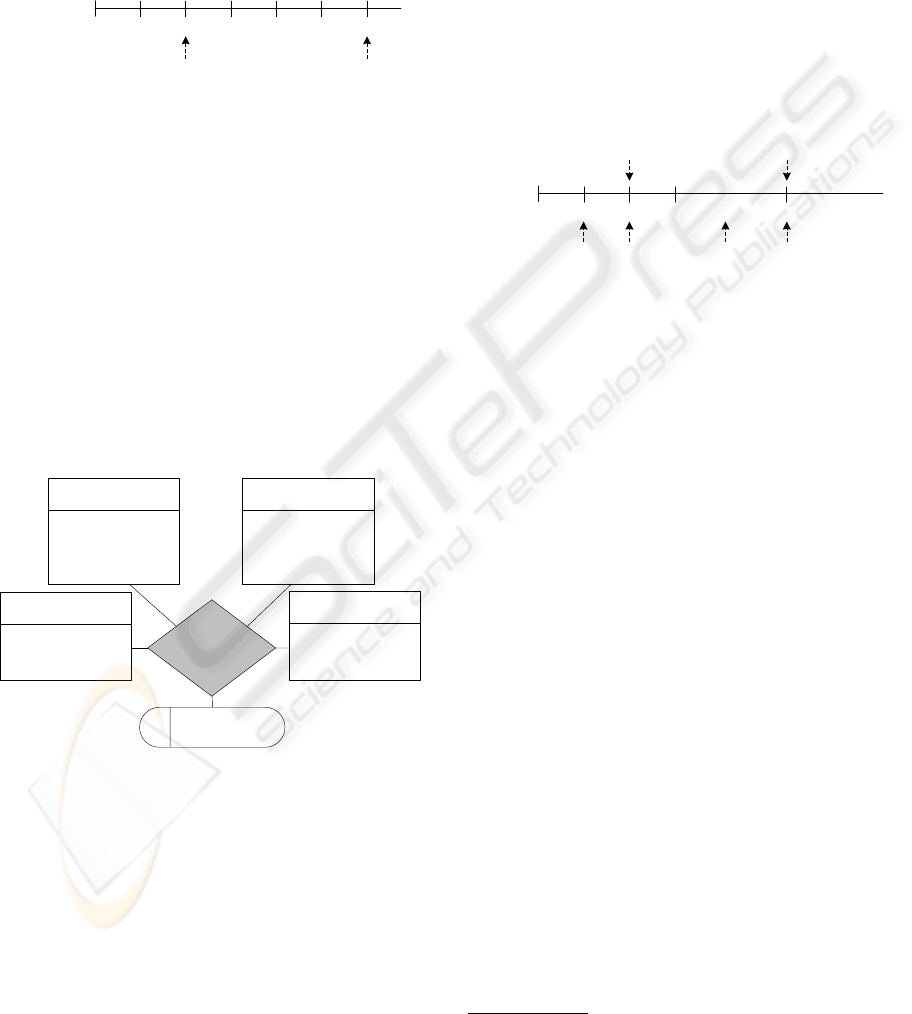
Case 4. Sources: VT, TDWs: VT and DWLT In
the previous two cases, we include VT in a TDW,
which is the most common practice. However, the ad-
dition of DWLT can give the information since when
the data has been available for the decision-making
process helping to better understand decisions made
in the past and to adjust loading frequencies.
100
DWLT
1
10
no sales
10
13
...
Sales
Time
(weeks)
11
5
200 500
20
12
14
DWLT
2
Figure 4: Example of having VT and DWLT.
For example, based on a growing tendency of prod-
uct sales during weeks 10, 11 and 12 (Figure 4), it
was decided to buy more products. However, only in
the next DW load, occurred eight weeks later, a sud-
den decrease of sales has been revealed. Thus, an ad-
ditional analysis can be performed to understand the
causes of these changes in sales behavior. Further, the
decision of more frequent loads may be taken.
Case 5. Sources: TT, TDWs: TT (DWLT, VT) DW
data can be needed for traceability applications (e.g.,
for fraud detection) where changes to data and time
when they have occurred should be available. That is
possible if source systems have TT.
Fraud
detection
Amount
TT
Insurance agency
Agency id
Agency address
Other attributes
Insurance object
Object id
Object name
Other attributes
Insurance type
Type id
Insurance name
Insurance category
Other attributes
Client
Client id
Client name
Client address
Other attributes
Figure 5: Example of a TDW for insurance company with
TT for representing time of measure changes.
An example given in Figure 5 is used for an insur-
ance company having as an analysis focus the amount
of insurance payments. Since investigators suspect
an internal fraud by modification of the amount of
insurance paid to clients, the detailed information
is required indicating when changes in measure val-
ues have been introduced. Further, the inclusion of
DWLT would give the additional information since
when data has been available for the investigation
process while the inclusion of VT would allow to
know when the payment was received by client. In
many real systems, the combination of both, TT and
VT, i.e., BT will be included.
Case 6. Sources: BT, TDWs: BT and DWLT TDW
data should offer a timely consistent representation of
information (Bruckner and Tjoa, 2002). Since some
delay may occur between the time when the data is
valid in the reality, when it is known in the sources,
and when it is stored in the DW, it is sometimes neces-
sary to include VT, TT and DWLT. Figure 6 shows an
example of the usefulness of having these three tem-
poral types. This example is based on the conceptual
model for managing temporal consistency in active
DWs (Bruckner and Tjoa, 2002).
100
DWLT
1
14
...
Salary
Time
(months)
2
8
3
DWLT
2
200
VT[2:5]
VT[6:NOW]
TT
1
TT
2
Figure 6: Example of having VT, TT, and DWLT.
In this example, a salary 100 with VT from the
second to fifth months was stored at the third month
(TT
1
) in a source system. Afterwards, at the eighth
month (TT
2
) a new salary was inserted with value
200 and VT from the sixth month until NOW. When
data was loaded into TDW at DWLT
1
, the value of the
salary was unknown. In the next loading DWLT
2
the
value 100 was stored in the TDW. However, depend-
ing on which instant of time users want to analyze
different values can be retrieved
7
.
5 TEMPORAL SUPPORT FOR
AGGREGATED MEASURES
In this section, we will analyze how to match different
time granularities between source and TDW systems
and how to aggregate measures to which these time
granules are attached. We also refer to temporal types
that can be used for aggregated measures in TDWs.
5.1 Different Time Granularities
Between Source Systems and
TDWs
Since TDW measures can be aggregated with regard
to time before loading, an adequate mapping between
multiple time granularities of a source system and a
7
For more details and analysis, readers can refer to
(Bruckner and Tjoa, 2002).
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
184
TDW should be considered. Two mappings are dis-
tinguished: regular and irregular (Dyrsen, 1994). In
the former, some conversion constant exists, so if one
granule is represented by an integer it can be con-
verted to another by a simple multiply or divide strat-
egy, e.g., minutes and hours or days and weeks.
In irregular mappings, granules cannot be con-
verted by a simple multiply or divide, e.g., month
and days, since each month is formed by a different
number of days. Thus, the mapping between different
granules must be specified explicitly.
Further, some mappings between different granu-
larities are not allowed (Bettini et al., 2000; Dyrsen,
1994), e.g., between weeks and months since a week
can belong to two months. Nevertheless, this situation
can be found in DW applications, e.g., the analysis of
employees’ salaries for each month having some em-
ployees with a salary received on weekly basis. We
call the mapping of such granularities forced.
5.2 Aggregation of Measures with
VT
After considering the mapping between different time
granularities, the aggregation of measure values must
be realized taking into account (1) applied functions,
e.g., sum, average and (2) type of measures, e.g., flow
or stock (Lenz and Shoshani, 1997).
However, in some cases the procedures for mea-
sure aggregations could be complex. A simplifying
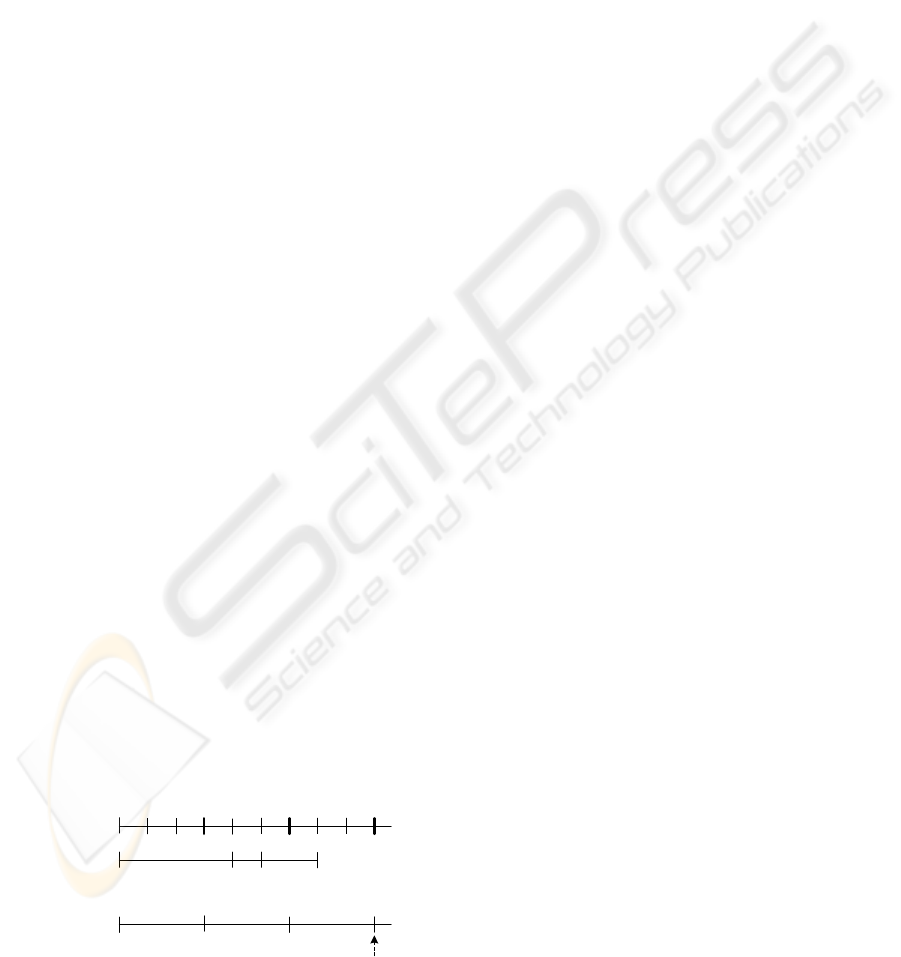
example is given in Figure 7 where the time granular-
ity in sources (month) requires a regular mapping to
DW granularity (quarter). This example includes dif-
ferent cases: (1) the same salary is paid during several
months overlapping different quarters (salary 20 and
40), (2) during a quarter different amounts of salary
can be paid (quarter 2), and (3) during several months
of a quarter an employee does not receive a salary
(quarter 3). The required measure is average salary
per quarter. For the first quarter, the average value is
calculated easily. The second quarter, simple average
does not work, thus the weighted mean value may be
given instead. However, for the third quarter, a user
should indicate how the value must be specified. In
the example, we opt for giving an undefined value.
20
13 6
12
Sources: month
Salary
DW: quarter
9
VT
1
3
30
40
VT
2
VT
3
20Avg. salary 30
?
DWLT
2
Figure 7: Example of coercion function for salary.
Real situations could be more complicated de-
manding clear specifications of coercion functions
(Merlo et al., 1999) or semantic assumptions (Bet-
tini et al., 2000). The idea of coercion functions
is not new in the TDB research community, e.g.,
(Merlo et al., 1999) use them for calculating values
attached to timestamps of different granularities be-
tween subtypes and supertypes or (Bettini et al., 2000)
for proposing a new framework for TDBs.
It should be noted that coercion functions are al-
ways required for the forced mapping, since a finer
time granule can map to more than one coarser time
granule, e.g., a week to two months. Therefore, mea-
sure values to which a finer granule is attached must
be distributed. For example, suppose that a salary is
paid on weekly basis and this measure is stored into
a TDW with a granule month. If the week belongs to
two months, e.g., January and February, a user may
specify that the percentage of salary that is assigned
for a month is obtained from the percentage of the
week contained in the month (e.g., 2 days from 7).
5.3 Temporal Types for Aggregated
Measures in TDWs
For aggregated measures, if source systems are non-
temporal, only DWLT can be included; if TT forms
part of source systems, this time will not be included
in a TDW. The purpose of having TT is to analyze
changes occurred to individual data, and TT for ag-
gregated data is meaningless.
On the other hand, VT may exist in source systems
for every individual measure. If measure values are
aggregated regarding time, VT must be adjusted to the
corresponding TDW granule. For example, the VT of
the aggregated measure of salary equal 20 in Figure 7
is equal 1 (quarter 1), even though VT for this salary
in a source system overlaps also quarter 2.
6 RELATED WORK
Most works related to TDWs include VT, e.g., (Body
et al., 2003; Eder et al., 2002; Mendelzon and Vais-
man, 2003). The inclusion of TT is a less common
practice and in Section 3 we already discussed exist-
ing approaches. Only (Bruckner and Tjoa, 2002) dis-
cuss the inclusion of VT, TT, and DWLT for active
data warehouses. However, unlike our approach, they
limit the usefulness of these temporal types for only
active DWs and do not offer a conceptual model that
includes these types.
Very few conceptual models for TDWs have been
proposed, e.g., (Body et al., 2003; Eder et al., 2002;
Mendelzon and Vaisman, 2003). These models for-
mally describe the temporal support for multidimen-
INCLUSION OF TIME-VARYING MEASURES IN TEMPORAL DATA WAREHOUSES
185

sional models. However, they are mainly concerned
about the temporal querying of data, correct aggrega-
tions, or evolutions of the multidimensional structure.
None of them refer to the features discussed in this
work, i.e., the inclusion of different temporal types
for measures and the problem of different time gran-
ularities between source systems and TDWs.
There are many works in TDBs related to transfor-
mations from finer to coarser (or vice versa) granular-
ities. For example, (Dyrsen, 1994) defines mappings
between different granularities as explained in Sec-
tion 5.1 while (Bettini et al., 2000) and (Merlo et al.,
1999) refer to the problem of conversion of differ-
ent time granularities and of handling data attached
to these granules
8
. On the other hand, multiple time
granularities for measures and dimensions are implic-
itly considered in (Eder et al., 2002). They mainly
focus on correct measure distributions between dif-
ferent temporal versions of dimension members.
Even though the aspect of managing data with
multiple time granularities is widely investigated in
TDBs, this is still an open research in TDWs.
7 CONCLUSIONS
TDWs extend DWs allowing to represent time-
varying multidimensional data. This extension is
based on the research achievements of TDBs and
should consider the semantic differences between
TDBs and DWs.
Based on a conceptual multidimensional model
called MultiDimER, we offer a temporal extension
for levels, hierarchies, and measures, ensuring that all
TDW elements are treated symmetrically. In this pa-
per, we referred to time-varying measures.
First, we proposed the inclusion in TDWs of dif-
ferent temporal types. Afterwards, we referred to two
different situations when the time granularity for rep-
resenting TDW measures is either the same or coarser
than the one in source systems. For the former, we
presented several cases justifying the inclusion of TT,
VT, or BT from source systems and of DWLT gen-
erated in a TDW. For the latter, we referred to exist-
ing proposals in TDBs that can be used in TDWs for
transformations of different time granularities and for
adequate handling of aggregations for measures. Fur-
ther, we presented different temporal types that may
be included for aggregated data, i.e., VT and DWLT.
The inclusion of temporal types in conceptual mod-
els allows to consider temporal semantics as an inte-
gral part of TDWs. Further, it allows to expand the
analysis spectrum for decision-making users.
8
More detailed references can be found, for example in
(Bettini et al., 2000).
REFERENCES
Bettini, C., Jajodia, S., and Wang, X. (2000). Time Gran-
ularities in Databases, Data Mining, and Temporal
Reasoning. Springer.
Body, M., Miquel, M., B
´
edard, Y., and Tchounikine, A.
(2003). Handling evolution in multidimensional struc-
tures. In Proc. of the 19th Int. Conf. on Data Engineer-
ing, pages 581–592.
Bruckner, R. and Tjoa, A. (2002). Capturing delays and
valid times in data warehouses – towards timely con-
sistent analyses. Journal of Intelligent Information
Systems, 19(2):169–190.
Dyrsen, C. (1994). Valid-Time Indeterminacy. PhD thesis,
University of Arizona.
Eder, J., Koncilia, C., and Morzy, T. (2002). The COMET
metamodel for temporal data warehouses. In Proc. of
the 14th Int. Conf. on Advanced Information Systems
Engineering, pages 83–99.
Jarke, M., Lenzerini, M., Y.Vassiluiou, and Vassiliadis, P.,
editors (2003). Fundamentals of Data Warehouse.
Springer.
Koncilia, C. (2003). A bi-temporal data warehouse model.
In Proc. of Short Papers of the 15th Int. Conf. on Ad-
vanced Information Systems Engineering, pages 77–
80.
Lenz, H. and Shoshani, A. (1997). Summarizability in
OLAP and statistical databases. In Proc. of the 9th
Int. Conf. on Scientific and Statistical Database Man-
agement, pages 132–143.
Malinowski, E. and Zim
´
anyi, E. (2005). Hierarchies in a
multidimensional model: from conceptual modeling
to logical representation. Accepted for publication in
Data & Knowledge Engineering.
Malinowski, E. and Zim
´
anyi, E. (2006). A conceptual so-
lution for representing time in data warehouse dimen-
sions. In Proc. of the 3rd Asia-Pacific Conf. on Con-
ceptual Modelling. Accepted.
Mart
´
ın, C. and Abell
´
o, A. (2003). A temporal study of data
sources to load a corporate data warehouse. In Proc.
of the 5th Int. Conf. on Data Warehousing and Knowl-
edge Discovery, pages 109–118.
Mendelzon, A. and Vaisman, A. (2003). Time in multidi-
mensional databases. In Rafanelli, M., editor, Multidi-
mensional Databases: Problems and Solutions, pages
166–199. Idea Group Publishing.
Merlo, I., Bertino, E., Ferrari, E., and Guerrini, G. (1999).
A temporal object-oriented data model with multiple
granularities. In 6th Int. Workshop on Temporal Rep-
resentation and Reasoning, pages 73–81.
Yang, J. and Widom, J. (1998). Mantaining temporal views
over non-temporal information source for data ware-
housing. In Proc. of the 6th Int. Conf. on Extending
Database Technology, pages 389–403.
ICEIS 2006 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
186
