
SECURE ONLINE ENGLISH AUCTIONS
Jarrod Trevathan
School of Mathematical and Physical Sciences
James Cook University
Wayne Read
School of Mathematical and Physical Sciences
James Cook University
Keywords:
Online auctions, event timing, anonymity, group signature.
Abstract:
Security and privacy in online auctions is a major concern as auction participants have many opportunities
to cheat (e.g., repudiate bids, not deliver items, etc.). Online auctions such as those used by eBay are based
on a type of auction referred to as an English auction. Dispite the English auction being the most popular
type of auction, it has received less security coverage than other types of auctions (e.g., sealed-bid auctions).
An existing proposal for a “secure” English auction prevents the Auctioneer from closing the auction early
and from blocking bids, but does not protect a bidder’s anonymity. Another proposal provides anonymity, but
does not stop an Auctioneer from skewing its clock or blocking bids. This paper proposes a new scheme for
conducting secure and anonymous online English auctions using a modified type of group signature. Trust
is divided among three servers owned by separate companies to ensure anonymity and fairness. Our scheme
solves the problems of the existing English auction schemes and has following characteristics: unforgeability,
anonymity, unlinkability, exculpability, coalition-resistance, verifiability, robustness, traceability, revocation,
one-off registration, unskewability and unblockability. Our scheme has comparable efficiency to the existing
schemes for the enhanced security and privacy it provides.
1 INTRODUCTION
Online auctioning is now widely accepted as one of
the premiere means to do business on the web. Eng-
lish auctions are the most common type of online auc-
tion employed by Internet auctioneers (e.g., eBay
1
and uBid
2
). Such auctions are used to sell various
items from real estate to football tickets. An Eng-
lish auction allows one seller to offer an item for sale.
Many potential buyers then submit bids for the item
attempting to outbid each other. The winner is the
bidder with the highest bid after a given time-out pe-
riod where no bid higher than the current highest bid
has been made. The winner must pay the seller an
amount equal to the winning bid.
Since the participants are not physically present in
an online auction, there exist many security concerns
and opportunities for people to cheat. For example, a
bidder might repudiate having made a bid or the seller
doesn’t deliver the item. Furthermore, the Auctioneer
could influence the auction in a manner inconsistent
1
http://www.ebay.com
2
http://www.ubid.com
with its rules (e.g., block bids). Security and privacy
in electronic auctions has been covered in (Boyd and
Mao, 2000; Franklin and Reiter, 1996; Naor et al.,
1991; Trevathan, 2005; Viswanathan et al., 2000),
and numerous “secure” auction schemes have been
proposed. However, most of the schemes presented
so far have been for sealed bid auctions (i.e., bids re-
main secret until the close of bidding). An English
auction on the other hand is an open bid auction (i.e.,
everyone knows the values of the bids). This com-
bined with the nature of the auctioning process makes
English auctions more complicated than regular cryp-
tographic auction schemes.
The timing of events in English auctions is much
more critical than sealed bid auctions. As a result, this
presents some unique security risks. An English auc-
tion requires a real-time link between the bidders and
the Auctioneer. Frequent price quotes are issued to
update bidders regarding the current highest bid. As
bidders base their decisions on this information, its
timeliness directly influences the auction. A corrupt
Auctioneer could disadvantage certain bidders by de-
laying this information or by speeding up (skewing)
the clock in order to close the auction early. Fur-
387
Trevathan J. and Read W. (2006).
SECURE ONLINE ENGLISH AUCTIONS.
In Proceedings of the International Conference on Security and Cryptography, pages 387-396
DOI: 10.5220/0002096603870396
Copyright
c
SciTePress

thermore, the speed and ease of the bid submission
process is significant, especially when an auction is
nearing its end. A malicious Auctioneer could selec-
tively block bids based on bidder identity and/or bid
value.
(Stubblebine and Syverson, 1999) presented an
English auction scheme that prevents the Auctioneer
from closing the auction early and from blocking bids.
However it does not protect a bidder’s anonymity.
Alternately, a scheme by (Omote and Miyaji, 2001)
provides anonymity, but does not stop an Auction-
eer from skewing its clock or blocking bids. We be-
lieve the short-comings of the existing schemes can
be solved by basing the auction protocol on a modi-
fied group signature scheme.
The concept of group signatures was introduced
by (Chaum and van Heyst, 1991). A group signa-
ture scheme allows members of a group to sign mes-
sages on behalf of the group, such that the resulting
signature does not reveal the identity of the signer.
Signatures can be verified with respect to a single
group public key. Only a designated group manager
is able to open signatures, and thus reveal the signer’s
identity. Due to these unique security characteristics,
group signature schemes have recently been used as
the basis for auction protocols (see (Trevathan et al.,
2005; Trevathan et al., 2006)).
This paper presents a scheme for conducting online
English auctions in a secure and anonymous manner.
The new scheme solves the problems of the existing
proposals while maintaining all of their features. The
role of the Auctioneer is divided among two auction
servers (owned by separate companies) to ensure that
the correct timing of events is maintained and to pre-
vent bid blocking. (see (Naor et al., 1991).) Our
scheme uses a group signature that is altered so that
the role of the group manager is also divided among
two indepedent auction servers. This allows for bid
verification and protects a bidder’s identity unless the
two servers collude. In the case of a dispute (e.g.,
a bidder repudiates a bid), a court order can be used
to reveal the bidder’s identity and he/she can be per-
manently revoked from the auction proceedings. The
scheme is flexible and allows the group signature to
be updated as better techniques for group signatures
become available. Our scheme offers comparable ef-
ficiency trade-offs for its enhanced security and pri-
vacy characteristics.
This paper is organised as follows: the remainder of
this section discusses security issues inherent in Eng-
lish auctions and our contribution. Existing English
auction schemes and their shortcomings are discussed
in Section 2. The components of our new scheme are
introduced in Section 3 and the auction protocol is
described in Section 4. An informal security analysis
of the new scheme is given in Section 5. Section 6
presents an efficiency comparision of the new scheme
and Section 7 provides some concluding remarks.
1.1 Fundamentals of Online English
Auctions
There are four main activities in an online English
auction:
Initialisation – The Auctioneer sets up the auction
and advertises it i.e., type of good being auctioned,
starting time, etc.
Registration – In order to participate in the auction,
bidders must first register with the Auctioneer.
Bidding – A registered bidder computes his/her bid
and submits it to the Auctioneer. The Auctioneer
checks the bid received to ensure that it conforms
with the auction rules.
Winner Determination – The Auctioneer determines
the winner according to the auction rules. Online
English auctions can terminate according to the fol-
lowing rules (see (Kumar and Feldman, 1998; Stub-
blebine and Syverson, 1999)):
1. Expiration Time - The auction closes at a predeter-
mined expiration time.
2. Timeout - The auction closes when no bids higher
than the current highest bid are made within a pre-
determined timeout interval.
3. Combination of Expiration and Timeout - The auc-
tion closes when there is a timeout after the expira-
tion time.
1.2 Security Issues in Online English
Auctions
The core security requirements for an English auction
include:
Unforgeability - Bids must be unforgeable, otherwise
a bidder can be impersonated.
Verifiability - There must be publicly available infor-
mation by which all parties can be verified as having
correctly followed the auction protocol. This should
include evidence of registration, bidding and proof of
the winner of the auction.
Exculpability - Neither the Auctioneer nor a legiti-
mate bidder can forge a valid signature of a bidder.
Coalition-resistance - No coalition of bidders can
frame an innocent bidder by fabricating a bid.
Robustness - The auction process must not be af-
fected by invalid bids or by participants not following
the correct auction protocol.
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
388

Anonymity - The bidder-bid relationship must be
concealed so that no bidder can be associated or iden-
tified with the bid they submit.
One-time registration - Registration is a one-off pro-
cedure, which means that once a bidder has regis-
tered, they can participate in future auctions held by
the Auctioneer.
Unlinkability - Bids are unlinkable within an auction,
and also between plural auctions.
Traceability - Once a bidder has submitted a bid, they
must not be able to repudiate having made it. Other-
wise if a bidder wins and does not want to pay, they
might deny that they submitted the winning bid. In
this event the identity of the bidder who submitted the
bid in question can be revealed.
Revocation - Malicious bidders can be easily revoked
from all future auctions.
English auctions are open bid and the timely nature
of the auction process therefore raises several further
concerns. Due to the flexibility of closing rules for
English auctions this introduces the following unique
requirements:
Unskewability - The Auctioneer must not be able to
alter the auction timing. For example, speed up its
clock in an attempt to close the auction early, or slow
the auction down to keep the bidding process active
beyond the official timeout.
Unblockability - The Auctioneer cannot selectively
block bids based on bid amount or the identity of the
bidder.
Conditional bid cancellation - In online auctions us-
ing an expiration time, it is common for the auction to
continue for days or weeks. In this situation a bidder
might be reluctant to make such an open ended bid.
Therefore depending on the closing rule and the stage
of the auction it is desirable to allow bidders to con-
ditionally cancel bids. Note that bidders should not
be able to cancel bids when an auction is in a timeout
stage and cancellation must only be done in strict ac-
cordance with the Auctioneer’s bid cancellation pol-
icy.
2 EXISTING ENGLISH AUCTION
SCHEMES
Discussions regarding security for English auctions
can be found in (Kumar and Feldman, 1998; Tre-
vathan et al., 2005). Several “secure” English auc-
tion schemes have been proposed by (Lee et al., 2001;
Nguyen and Traore, 2000; Omote and Miyaji, 2001;
Stubblebine and Syverson, 1999). The first scheme
is due to (Stubblebine and Syverson, 1999). This
scheme requires bidders to register with the Auction-
eer. The Auctioneer must periodically timestamp the
auction proceedings with a Notary to prove to bid-
ders that it is not skewing its clock. Bidders submit
bids using a reverse hash chain and secret bid com-
mitments. This is done to ensure that the Auctioneer
cannot block bids, and that bidders are not able to re-
pudiate bids. The auction proceedings are recorded
on a public bulletin board that is readable by every-
one, but can only be written to by the Auctioneer.
We have identified the following problems with this
scheme:
1. There is no anonymity for the bidders.
2. Bids are linkable, meaning that the Auctioneer can
create profiles about individual bidders and their
bidding strategies.
3. All parties must trust the Notary. (i.e., to ensure the
correct timing is maintained.)
(Omote and Miyaji, 2001) refine a scheme by
(Nguyen and Traore, 2000) that uses a form of mod-
ified group signature (Ateniese et al., 2000; Ca-
menisch and Stadler, 1997; Chaum and van Heyst,
1991). This scheme allows a bidder to register once
and participate in any number of auctions held by the
Auctioneer. Bids are claimed to be unlinkable be-
tween different auctions, but linkable within a partic-
ular auction. This is achieved by requiring the bidder
to calculate a new signature generation key prior to
each auction.
In this scheme there are two mangers responsible
for conducting the auction. The Registration Man-
ager (RM) secretly knows the correspondence of the
bidder’s identity and registration key. RM works as an
identity escrow agency. The Auction Manager (AM)
hosts the auction and prepares bidder’s auction keys
in each round.
We have identified the following problems with this
scheme:
1. All bidders must update their keys between each
round of auctioning, which is essentially equiva-
lent to re-registering. Therefore, this negates the
author’s claims that registration is a one-off proce-
dure.
2. AM can skew its clock and/or selectively block
bids.
3. Revoking a bidder is inefficient as it requires AM
to reissue new keys to all of the existing bidders.
4. (Lee et al., 2001) describe a flaw in this scheme
during the winner announcement stage. Here AM
is able to erroneously inform any bidder that they
have won without being publicly verifiable. Lee et
al. propose a solution. However, this introduces
several more bulletin boards and requires computa-
tions that are an order of magnitude slower.
5. Bids are linkable within a current auction, but un-
linkable between plural auctions. The motivation
SECURE ONLINE ENGLISH AUCTIONS
389

for this is stated as the auction participants gain
utility in terms of entertainment from viewing the
auction. For example, when there is a rally between
two particular bidders, observers enjoy knowing
how many bids a bidder has submitted.
With regard to the last point, it is our opinion, that
in an anonymous auction scheme all bids (whether
in the same auction or not) must be totally unlink-
able. Observers can still see a rally, however, there is
no need to know exactly whom the bids are coming
from. Our scheme described in the next section, does
not allow bids to be linked within the same auction or
between plural auctions.
3 COMPONENTS OF OUR
SCHEME
The auction has four parties:
A Bidder, who is interested in buying an item from a
seller in an English auction.
An Auction Manager (AM), who organises the
auction proceedings, accepts bids and determines
the winner according to whoever has submitted the
highest bid. To participate in an auction, a bid-
der presents his/her real identity to AM. AM issues
the bidder with a token that allows him/her to register.
A Registration Manager (RM), who takes part in the
protocol in order to complete the registration of a
bidder, once a token has been obtained from AM. At
the end of the protocol, the bidder obtains a secret
key that enables him/her to generate signed bids in a
proper format.
An Auction Helper (AH), who aids AM in accepting
bids and determining the winner. AH is owned by a
separate company and is tasked with ensuring that
AM does not alter its clock or block bids.
The scheme uses a two-server trust approach that
can be broken down into two subsystems: the
anonymity subsystem and the auction subsystem (see
Figure 1). The anonymity subsystem protects the
anonymity of the bidders provided the AM and RM
do not collude. The auction subsystem ensures the
correct outcome of the auction as long as AM and AH
do not collude. There is no trust assumed between
RM and AH.
Each bidder, AM and AH are connected to a com-
mon broadcast medium with the property that mes-
sages sent to the channel instantly reach every party
connected to it. The broadcast channel is public so
that everybody can listen to all information commu-
nicated via the channel, but cannot modify it. It is
also assumed that there are private channels between
RM and any potential bidders (who wish to join the
auction proceedings).
3.1 Group Signatures
To join an auction, a bidder must first register with
RM (who plays the role of a group manager in a group
signature scheme). Once registered, a bidder can par-
ticipate in the auction by signing bids using the group
signature. Bids are submitted to an independent AM
who runs the auction (with the help of AH which is
explained later). AM (and AH) post the auction re-
sults on a publicly verifiable bulletin board.
One of the most efficient and popular proposals for
group signature schemes is due to (Ateniese et al.,
2000). This is the group signature scheme that is used
for the basis of our auction protocol. The (Ateniese et
al., 2000) group signature scheme informally works
as follows:
Let n = pq be an RSA modulus, where p and q are
two safe primes (i.e., p = 2p
′
+ 1, q = 2q
′
+ 1, and
p
′
, q
′
are also prime numbers). Denote by QR(n), the
set of quadratic residues - a cyclic group generated
by an element of order p
′
q
′
. The group public key
is Y = (n, a, a
0
, y = g
x
, g, h), where a, a
0
, g, h are
randomly selected elements from QR(n). The secret
key of the group manager is x.
To join the group, a user (bidder i) must engage in
a protocol with the group manager (i.e., RM and AM)
and receive a group certificate [B
i
, e
i
] where B
i
=
(a
x
i
, a
0
)
1/e
i
mod n with e
i
and x
i
chosen from two
integral ranges as defined in (Ateniese et al., 2000).
(x
i
is only known to the user/bidder).
In order to sign a message/bid, m, the user/bidder
has to prove possession of his member certificate
[B
i
, e
i
] without revealing the certificate itself. More
precisely, the user/bidder computes:
T
1
= B
i
y
w
mod n, T
2
= g
w
mod n,
T
3
= g
e
i
h
w
mod n SK(m)
where the value SK(m), computed over a message
m, indicates a signature of knowledge of the secret
key x
i
and the e
i
th root of the first part of the repre-
sentation of T
3
(in the implementation of our scheme,
the exact signature generation and verification proce-
dures will be presented).
In the case of a dispute, the group manager can
open a signature that reveals the identity of the signer.
This is due to the fact that the pair (T
1
, T
2
) is an El-
Gamal encryption of the user’s certificate (using the
public key of the group manager). That is, the group
manager can compute B
i
, using B
i
= T
1
/(T
2
)
x
.
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
390
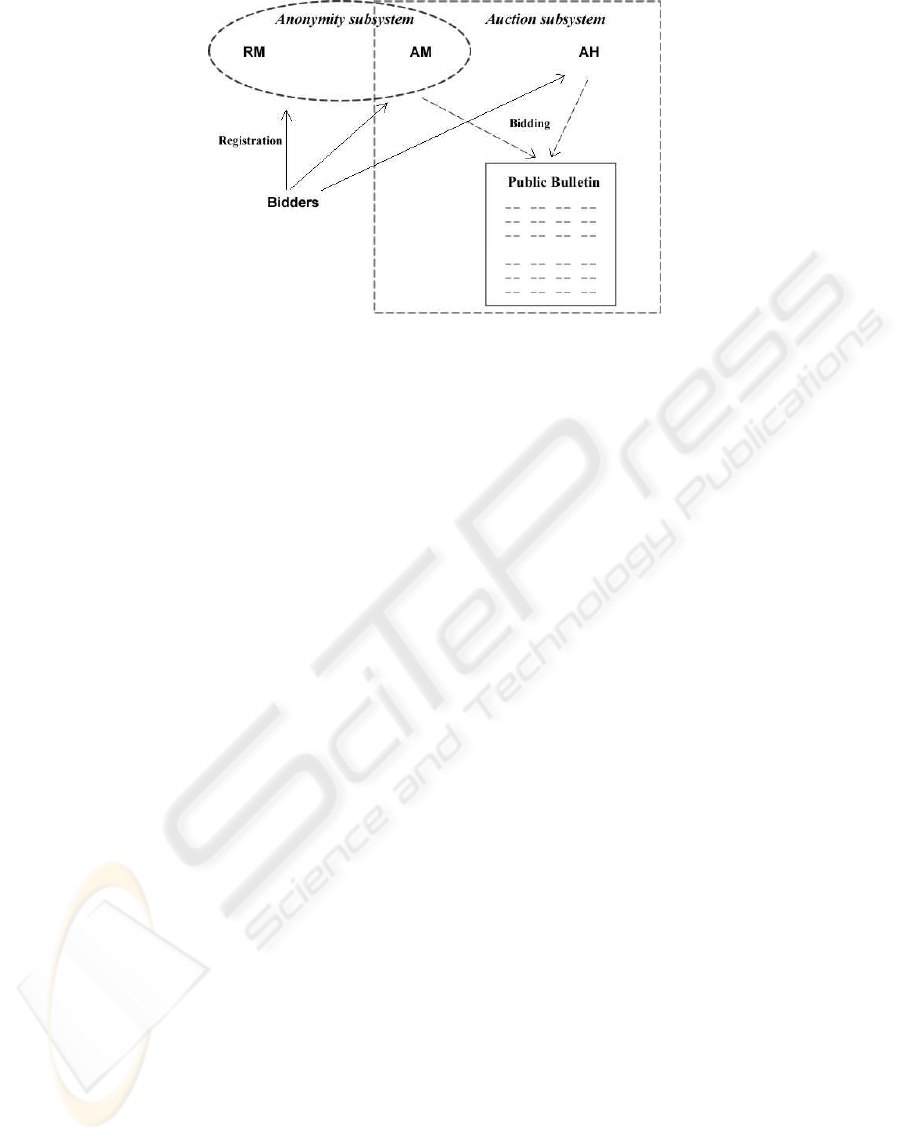
Figure 1: The Auction Model.
In certain circumstances users must be revoked
from the group. For example, a membership expires
or a user misbehaves. Reissuing keys to all existing
group members is unwieldy and inefficient for a large
group. Using a certificate revocation list to blacklist
malicious bidders requires the verifier of the signature
to check a list that is linear in the number of revoked
users.
(Camenisch and Lysyanskaya, 2002) propose a
scheme based on a dynamic accumulator that requires
a member to prove that they have not been revoked.
Informally, an accumulator is a method to combine
a set of values into one short accumulator such that
there is a short witness that a given value was incor-
porated into the accumulator. It is infeasible to find a
witness for a value that is not in the accumulator. A
dynamic accumulator allows values to be added and
deleted from the accumulator at unit cost. By incor-
porating dynamic accumulators into a group signature
scheme, revocation can easily be performed by delet-
ing a member’s value from the accumulator.
A user must check the accumulator prior to signing.
This requires an online link between the group man-
ager and the users. In terms of an auction, a bidder
must check the accumulator each time they submit a
bid. This is reasonable for English auctions, as there
is a real-time communication link between the Auc-
tioneer and bidders anyway.
The (Camenisch and Lysyanskaya, 2002) dynamic
accumulator scheme can be defined as follows: A
dynamic accumulator for a family of inputs {X
1
}
is a family of families of functions {F
1
} with the
following properties:
Efficient generation: There is an efficient proba-
bilistic algorithm G that on input 1
k
produces a ran-
dom element f of F
k
. Moreover, along with f, G also
outputs some auxiliary information about f, denoted
aux
f
.
Efficient evaluation: f ∈ F
k
is a polynomial-size
circuit that, on input (u, k) ∈ U
f
× X
k
, outputs a
value v ∈ U
f
, where U
f
is an efficiently-samplable in-
put domain for the function f; and X
k
is the intended
input domain whose elements are to be accumulated.
Quasi-commutative: For all k, for all f ∈ F
k
for
all u ∈ U
f
for all x
1
, x
2
∈ X
k
, f(f (u, x
1
), x
2
) =
f(f(u, x
2
), x
1
). If X = {x
1
, ..., x
m
} ⊂ X
k
, then by
f(u, X ) we denote f(f(...(u, x
1
), ...), x
m
).
Witness: Let v ∈ U
f
and x ∈ X
k
. A value w ∈ U
f
is called a witness for x in v under f if v = f(w, x).
Addition: Let f ∈ F
1
, and v = f(u, X ) be the
accumulator so far. There is an efficient algorithm A
to accumulate a given value x
′
∈ X
1
. The algorithm
outputs:
1. X
′
= X ∪ {x
′
} and v
′
= f(v, x
′
) = f(u, X
′
);
2. w
′
which is the witness for x ∈ X in v
′
.
Deletion: Let f ∈ F
1
, and v = f (u, X ) be the
accumulator so far. There exist efficient algorithms
D, W to delete an accumulated value x
′
∈ X . The
functionality of the algorithms includes:
1. D(aux
f
, v, x
′
) = v
′
such that v
′
= f(u, X {x
′
}),
and
2. W(w, x, x
′
, v, v
′
) = v
′
such that f(w
′
, x) = v
′
,
where x ∈ X and f(w, x) = v.
The (Camenisch and Lysyanskaya, 2002) dynamic
accumulator scheme is based on the strong RSA
assumption and accumulates prime numbers (i.e.,
the primes used for the membership certificates in
(Ateniese et al., 2000) group signature scheme).
The scheme also provides a proof that a committed
value was accumulated (we will omit these details).
The construction of a dynamic accumulator where
the domain of accumulated values consists of prime
numbers, is as follows:
SECURE ONLINE ENGLISH AUCTIONS
391

- F
k
is the family of functions that correspond to ex-
ponentiating modulo-safe prime products drawn from
the integers of length k. Choosing f ∈ F
k
amounts
to choosing a random modulus n = pq of length k,
where p = 2p
′
+ 1, q = 2q
′
+ 1, and p, p
′
, q, q
′
are all
prime. We will denote f corresponding to modulus n
and domain X
A,B
by f
n,A,B
.
- X
A,B
is the set {e ∈ primes : e 6= p
′
, q
′
∧ A ≤
e ≤ B}, where A and B can be chosen with arbitrary
polynomial dependence on the security parameter k,
as long as 2 < A and B < A
2
. X
′
A,B
is (any subset
of) of the set of integers from [2, A
2
− 1] such that
X
A,B
⊆ X
′
A,B
.
- For f = f
n
, the auxiliary information aux
f
is the
factorisation of n.
- For f = f
n
, U
f
= {u ∈ QR
n
: u 6= 1} and U
′
f
=
Z
∗
n
.
- For f = f
n
, f(u, x) = u
x
mod n. Note that
f(f(u, x
1
), x
2
) = f(u(x
1
, x
2
)) = u
x
1
x
2
mod n.
- Update of the accumulator value. Adding a value
˜x to the accumulator value v can be done as v
′
=
f(v, ˜x) = v
˜x
mod n. Deleting a value ˜x from
the accumulator is as follows: D((p, q), v, ˜x) =
v
˜x−1 mod (p−1)(q−1)
mod n.
- Update of a witness. Updating a witness u after ˜x
has been added can be done by u
′
= f(u, ˜x) = u
˜x
.
In case, ˜x 6= x ∈ X
k
has been deleted from the accu-
mulator, the witness u can be updated as follows. By
the extended GCD algorithm, one can compute the
integers a, b such that ax + b˜x = 1 mod n and then
u
′
= W(u, x, ˜x, v, v
′
) = u
b
v
′a
.
4 THE AUCTION PROTOCOL
This section describes the auction protocol. A high
level view of the protocol is given in Figure 2.
Lines dipict communication between parties while the
dashed circles indicate stages in the protocol. Lines
that pass through the dashed circles are communica-
tions that are performed during the particular stage.
4.1 Setup
Most activities of this stage need to be performed only
once (in order to establish the auction proceedings).
Let λ
1
, λ
2
, γ
1
, and γ
2
be some lengths, Λ, Γ be some
integral ranges, and H(.) be a collision-resistant hash
function. RM sets up the group public key and his
secret key by performing the following steps:
1. Chooses two safe primes p and q (i.e., p = 2p
′
+ 1
and q = 2q
′
+ 1, where p
′
and q
′
are prime num-
bers) and sets the RSA modulus n = pq
2. Chooses random elements a, a
0
, g, h ∈ QR(n)
3. Chooses a secret element x ∈
R
Z
∗
p
′
q
′
and sets y =
g
x
mod n
4. Publishes the group public key as Y =
(n, a, a
0
, y, g, h)
5. Creates the public modulus n for the accumulator,
chooses a random u ∈ QR
n
and publishes (n, u)
6. Set up (empty for now) public archives E
add
for
storing values that correspond to added users and
E
delete
for storing values that correspond to deleted
users
4.2 Registration
A user submits a request to AM to participate in the
auction proceedings. AM verifies the identity of the
requestor, and issues a token that is verifiable by RM.
The user then takes part in a protocol with RM, in
order to obtain his/her secret key and a certificate of
membership in the auction proceedings. Note that
the token does not carry the real identity of the bid-
der. All communication between RM and the owner
of a token is authenticated and recorded. The pro-
tocol between a new bidder i, and RM is as follows
(checks in which values are chosen from proper in-
tervals, the user knows discrete logarithms of values,
etc. are omitted):
1. Bidder i selects random exponents x
′
i
, r and sends
C
1
= g
x
′
i
h
r
mod n to the RM
2. RM checks that C
1
∈ QR(n). If this is the case,
RM selects random values α
i
, β
i
and sends them to
bidder i
3. Bidder i computes x
i
= 2
λ
1
+(α
i
x
′
i
+β
i
mod 2
λ
2
)
and sends to RM the value C
2
= a
x
i
mod n
4. RM checks that C
2
∈ QR(n). If this is the
case, RM selects a random e
i
∈ Γ and computes
B
i
= (C
2
a
0
)
1/e
i
mod n then sends the member-
ship certificate [B
i
, e
i
] to bidder i (note that B
i
=
(a
x
i
a
0
)
1/e
i
mod n)
5. Bidder i verifies that a
x
i
a
0
= B
e
i
i
mod n
6. Add the current u to the bidder’s membership cer-
tificate. Update u: u = f
n
(u, e
i
). Update E
add
:
store e
i
there
7. Verify that f
n
(u
i
, e
i
) = u
e
i
i
= u
RM creates a new entry in the membership table
and stores bidder i’s membership certificate [B
i
, e
i
]
and a transcript of the registration process in this lo-
cation.
4.3 Setup - Before Each Auction
AM organises the auction (i.e., advertising and calls
for auction). AM posts information to the bulletin
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
392
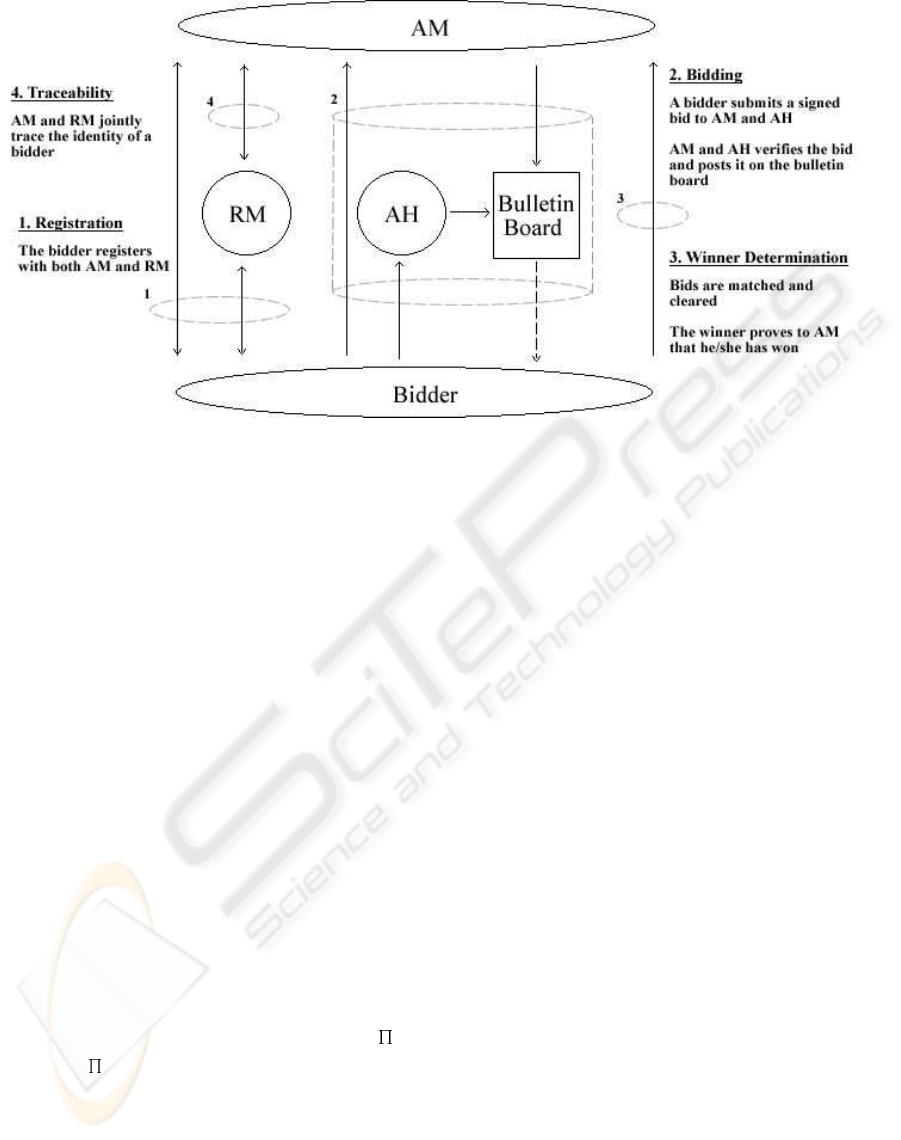
Figure 2: The Auction Protocol.
board regarding the auction including the auction id
(which uniquely identifies the auction), the reserve
price (minimum winning price that will be accepted),
the auction starting time and the auction closing rules.
4.4 Bidding
Using a membership certificate [B
i
, e
i
], a bidder can
generate anonymous and unlinkable group signatures
on a bid m. m contains the auction id and the amount
of the bid (i.e., m = id k bid value). Bidder i submits
a bid m to both AM and AH signed using his/her
secret key.
Update Membership - Prior to submitting a bid, a
bidder must check if there have been any changes to
the group (i.e., new bidders have been added, or other
bidders have been revoked). If this is the case, a bid-
der must perform a membership update. This is done
as follows:
An entry in the archive is called “new” if it was en-
tered after the last time bidder i performed an update.
1. Let y denote the old value of u
2. For all new e
j
∈ E
add
, u
i
= f(u
i
,
Q
e
j
) = u
e
j
i
and y = y
e
j
3. For all new e
j
∈ E
delete
, u
i
=
W (u
i
, e
i
,
Q
e
j
, y, u) (Note that as a result
u = f (u
i
, e
i
))
Sign Bid - In order to generate a signature on a mes-
sage/bid, m, bidder i performs the following:
1. Chooses a random value w and computes:
T
1
= B
i
y
w
mod n, T
2
= g
w
mod n,
T
3
= g
e
i
h
w
mod n
2. Chooses r
1
, r
2
, r
3
, r
4
(randomly) from predeter-
mined intervals and computes:
(a) d
1
= T
r
1
1
/(a
r
2
y
r
3
), d
2
= T
r
1
2
/(g
r
3
), d
3
=
g
r
4
, and d
4
= g
r
1
h
r
4
(all in mod n),
(b) c = H(g k h k y k a
0
k a k T
1
k T
2
k T
3
k
d
1
k d
2
k d
3
k d
4
k m),
(c) s
1
= r
1
− c(e
i
− 2
ξ
1
), s
2
= r
2
− c(x
i
− 2
λ
1
),
s
3
= r
3
− ce
i
w, and s
4
= r
4
− cw (all in Z).
3. In addition to T
1
, T
2
, and T
3
the bidder com-
putes the values C
e
= g
e
h
r
1
, C
u
= uh
r
2
, and
C
r
= g
r
2
h
r
3
and sends them to AM, with random
choices r
1
, r
2
, r
3
∈
R
Z
[n/4]
4. The output is
(c, s
1
, s
2
, s
3
, s
4
, r
1
, r
2
, r
3
, r
4
, T
1
, T
2
, T
3
, C
e
, C
u
, C
r
)
Prove Membership/Verify Bid - AM and AH check
the validity of the bidder’s signature using the group’s
public key Y. A bid of the correct form is considered
to be valid and is included in the auction (i.e., posted
on the bulletin board). An invalid bid is discarded.
There are two copies of the bid on the bulletin, one
posted by AM and the other posted by AH. AM and
AH verify the signature on the bid as follows:
1. Compute (all in mod n):
c
′
= H(g k h k y k a
0
k a k T
1
k
T
2
k T
3
k (a
c
0
T
(s
1
−c2
ξ
1
)
1
)/(a
s
2
−c2
λ
1
y
s
3
) k
(T
s
1
−c2
ξ
1
2
)/(g
s
3
) k T
c
2
g
s
4
k T
c
3
g
s
1
−c2
ξ
1
h
s
4
k m)
SECURE ONLINE ENGLISH AUCTIONS
393

2. AM, AH and the bidder engage in a protocol to
prove membership (see (Camenisch and Lysyan-
skaya, 2002) for details)
3. Accept the signature if and only if c = c
′
, and the
parameters s
1
, s
2
, s
3
, s
4
lie in the proper intervals
Bid Cancellation - If a bidder desires to cancel a bid,
they must send a copy of the bid they wish to cancel
and a CANCEL message signed using his/her group
key to both AM and AH. Upon receiving the CAN-
CEL message, AM and AH check the bidder’s signa-
ture on the message using the group’s public key Y.
If the signature is valid, AM and AH then check what
stage the auction is in. If the auction close rule is cur-
rently in an expiration time stage, AM and AH each
post a message to the bulletin stating that the particu-
lar bid has been cancelled. If the auction is currently
in a timeout stage, the CANCEL message is discarded
and the bid remains in effect.
4.5 Winner Determination
Once the auction has closed, AM and AH then deter-
mine the auction outcome according to which bidder
has made the highest bid. The winning bidder can
produce a copy of the signed bid as evidence that they
have won.
4.6 Traceability
In the event of a dispute, RM (with the help of AM)
can open the signature on a bid to reveal which bidder
is the original signer. This process is as follows:
1. Check the signature’s validity via the verification
procedure
2. Recover B
i
(and thus the identity of bidder i) as
B
i
= T
1
/T
2
x
mod n
RM then checks the registration transcripts, and
determines the token associated with this certificate.
AM, who knows the relation between tokens and real
identities, can determine the identity of the bidder.
Note that in our scheme, revealing the identity of a
bidder does not reveal any information about his/her
past bids.
4.7 Revocation
When a bidder has been caught breaking the auction
rules, they can be permanently revoked from the auc-
tion proceedings by cancelling the bidder’s ability to
sign future bids. To achieve this, the bidder’s prime
number used in his/her membership certificate is not
included when the dynamic accumulator is updated.
This can be done as follows: Retrieve e
i
which is the
prime number corresponding to the bidder’s member-
ship certificate. Update u: u = D(ψ(n), u, e
i
). Up-
date E
delete
: store e
i
there.
5 SECURITY
This section provides an informal security analysis
of the online English auction scheme presented in
this paper based on the characteristics described in
Section 1.2.
Unforgeability - Only bidders that are members of
the group are able to sign messages on behalf of the
group. This is due to the unforgeability of the under-
lying group signature.
Anonymity - Given a valid signature
(c, s
1
, s
2
, s
3
, s
4
, T
1
, T
2
, T
3
) identifying the ac-
tual signer is computationally difficult. Determining
which bidder with certificate [B
i
, e
i
] has signed a
bid, requires deciding whether the three discrete
logarithms log
y
T
1
/B
i
, log
g
T
2
, and log
g
T
3
/g
e
i
are equal. This is assumed to be infeasible under
the decisional Diffie-Hellman assumption, and thus
anonymity is guaranteed. Note that in our auction,
RM can figure out the certificate associated with each
signature, but cannot determine the identity of the
bidder associated with this certificate.
Unlinkability - Deciding if two signatures
(c, s
1
, s
2
, s
3
, s
4
, T
1
, T
2
, T
3
) and
(ec, es
1
, es
2
, es
3
, es
4
,
f
T
1
,
f
T
2
,
f
T
3
) were computed by the
same bidder is computationally hard (with the same
argument as for anonymity).
Exculpability - Neither a bidder nor AM, AH and/or
RM can sign on behalf of another bidder. This is be-
cause the secret key x
i
, associated to user i is com-
putationally hidden from RM. RM, at most, can learn
a
x
i
mod n, which cannot help him to learn the ex-
ponent x
i
(since the discrete logarithm over the safe
composite modulo n, is difficult).
Coalition-resistance - This is due to the follow-
ing theorem: (Ateniese et al., 2000) Under the
strong RSA assumption, a group certificate [B
i
=
(a
x
i
a
0
)
1/e
i
mod n, e
i
] with x
i
∈ Λ and e
i
∈ Γ can
be generated only by the group manager provided that
the number K of certificates the group manager issues
is polynomially bounded.
Verifiability - All bids (including signatures) are
posted to the public bulletin, therefore all parties can
verify the auction outcome.
Robustness - Invalid bids will not be posted to the
bulletin board. Moreover, malicious bidders will be
revoked from the system, and thus cannot affect the
auction outcome.
Traceability - RM is always able to open a valid sig-
nature and, with the help of AM, identify the signer
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
394

Table 1: Comparison of CDA schemes.
SS99 OM001 Our Scheme TX03
Registration 1 exp. 480 mul. 30 exp. 2 exp.
Signing 1 exp. 240 mul. 25 exp. 17 exp.
Verification 1 exp. 320 mul. 21 exp. 16 exp.
Revocation N/A O(ℓ) O(1) O(1)
of the bid.
Revocation - Bidders can be easily revoked from
the future auctions if they have broken the auction
rules. See theorem 2 in (Camenisch and Lysyanskaya,
2002).
One-time registration - Once a bidder has received
a signature generation key, they are free to participate
in future auctions.
Unskewability - AH observes AM’s clock (and vice
versa) therefore any clock skews will not go unno-
ticed. AM’s clock can be trusted as long as both AM
and AH do not collude.
Unblockability - A bidder must submit his/her bids
to both AM and AH, who post the bid on the bulletin
board. If either tries to block a bid, then only one
confirmation of the bid will be posted to the bulletin
board which will indicate that one of the parties has
blocked a bid. Bids cannot be blocked unless AM and
AH collude.
Conditional bid cancellation - Bidders can condi-
tionally cancel bids by sending a CANCEL message
to AM and AH as long as the auction is not in a time-
out stage.
6 EFFICIENCY
This section discusses the efficiency considerations of
the new scheme. We contrast our approach with the
existing English auction schemes. Table 1 shows the
amount of work performed during each major stage
of the auction in terms of the number of modular ex-
ponentiations (exp) or multiplications (mul) required.
The schemes compared include: (Stubblebine and
Syverson, 1999) (SS99), (Omote and Miyaji, 2001)
(OM01), our scheme, and (Tsudik and Xu, 2003)
(TX03). ((Tsudik and Xu, 2003) is an alternate im-
plementation of our approach.)
The registration, signing and verification proce-
dures for SS99 are relatively efficient. However, SS99
do not protect a bidder’s identity, nor do they dis-
cuss revocation issues. To incorporate revocation into
this scheme, it is likely that the registration procedure
would have to be repeated between auctions. Further-
more, SS99 do not address the issue of one-time reg-
istration. Once again bidders would have to repeat
the registration process for each auction they want to
participate in.
OM01 is significantly less efficient than SS99.
OM01 does not address bid cancellation whereas
SS99 does. Furthermore, OM01 does not prevent
the Auctioneer from skewing its clock. However,
OM01 protects a bidders identity and addresses one-
time registration. The cost of one-time registration
in OM01 is issuing new keys to bidders between auc-
tions, which is essentially equivalent to re-registering.
The revocation method in OM01 is tied in with the
one-time registration mechanism and therefore must
also be repeated between each auction. To revoke a
bidder requires the Auctioneer to perform work pro-
portional to O(ℓ) where ℓ is the number of bidders.
In contrast, our scheme has the most practical one-
time registration procedure. That is, once a bidder has
registered, there is no work required to retain mem-
bership other than regularly checking the accumula-
tor. We address bid cancellation, clock-skewing and
privacy concerns. To revoke a bidder, the Auction-
eer only has to update the accumulator. Bidders must
check the accumulator value prior to each bid which
is a constant operation. Our auction scheme can also
be implemented using TX03 which has significant ef-
ficiency gains.
The efficiency of our scheme is comparable to
the existing proposals. First of all our scheme has
an enhanced set of security requirements that are
much more comprehensive. Furthermore, our scheme
clearly has the most efficient revocation method. In
addition, we have the most practical one-time regis-
tration procedure.
7 CONCLUSIONS
This paper presented a scheme for conducting se-
cure and anonymous online English auctions. Such
a scheme is vital for protecting the security and
anonymity of participants who engage in online auc-
tioning. The timeliness of information and verifia-
bility of the Auctioneer’s actions is critical in an on-
line English auction. We have shown that the exist-
ing “secure” English auction schemes are inadequate
for the task. The scheme by (Stubblebine and Syver-
SECURE ONLINE ENGLISH AUCTIONS
395

son, 1999) does not provide anonymity for the bid-
ders and requires all parties to trust a public Notary.
The scheme by (Omote and Miyaji, 2001) does not
prevent an Auctioneer from skewing his/her clock or
from blocking bids.
In direct contrast, our scheme solves all of the prob-
lems of the existing schemes and has a more compre-
hensive set of security requirements. We use a group
signature to provide verification of bids and to pro-
tect the identities of bidders. The group signature is
modified so that the identity of a bidder is divided
among two separate parties (i.e., the anonymity sub-
system). The role of the Auctioneer is also divided
among two parties to prevent clock-skewing and bid-
blocking (i.e., the auction subsystem). The scheme
has comparable efficiency to the existing proposal for
its enhanced security and privacy characteristics. The
efficiency and security of the scheme rests with the
underlying group signature scheme used. Our ap-
proach offers the client flexibility in choosing from
any group signature scheme. The scheme offers effi-
cient one-time registration and revocation procedures
that are clearly better suited to handling multiple auc-
tions than existing proposals.
REFERENCES
Ateniese, G., Camenisch, J., Joye, M. and Tsudik, G.
(2000). A practical and provably secure coalition se-
cure coalition-resistant group signature scheme in Ad-
vances in Cryptology - Proceedings of CRYPTO 2000,
vol. 1880 of Lecture Notes in Computer Science,
Springer-Verlag, 255-270.
Ateniese, G., Song, D. and Tsudik, G. (2002). Quasi-
Efficient Revocation of Group Signatures, in Proceed-
ings of Financial Cryptography, vol. 2357 of Lecture
Notes in Computer Science, Springer-Verlag, 183-
197.
Boyd, C. and Mao, W. (2000). Security Issues for Elec-
tronic Auctions, Technical Report, Hewlett Packard,
TR-HPL-2000-90.
Camenisch, J. and Lysyanskaya, A. (2002). Dynamic Ac-
cumulators and Application to Efficient Revocation of
Anonymous Credentials, in Advances in Cryptology -
Proceedings of CRYPTO 2002, vol. 2442 of Lecture
Notes in Computer Science, Springer-Verlag, 61-76.
Camenisch, J. and Stadler, M. (1997). Efficient Group
Signature Scheme for Large Groups, in Advances
in Cryptology - Proceedings of CRYPTO ’97, vol.
1294 of Lecture Notes in Computer Science, Springer-
Verlag, 410-424.
Chaum, D. and van Heyst, E. (1991). Group Signatures,
in Advances in Cryptology - Proceedings of EURO-
CRYPT’91, vol. 547 of Lecture Notes in Computer
Science, Springer-Verlag, 257-265.
Franklin, M. and Reiter, M. (1996). The Design and Imple-
mentation of a Secure Auction Service, IEEE Trans-
actions on Software Engineering, vol. 22, 302-312.
Kumar, M. and Feldman, S. (1998). Internet Auctions, in
Proceedings of the Third USENIX Workshop on Elec-
tronic Commerce, 49-60.
Lee, B., Kim, K. and Ma, J. (2001). Efficient Public Auc-
tion with One-time Registration and Public Verifiabil-
ity, in International Conference on Cryptology in In-
dia - Proceedings of INDOCRYPT 2001, vol. 2247 of
Lecture Notes in Computer Science, Springer-Verlag,
162-174.
Naor, M., Pinkas, B. and Sumner, R. (1999). Privacy Pre-
serving Auctions and Mechanism Design, in The 1st
ACM Conference on Electronic Commerce, 129-139.
Nguyen, K. and Traore, J. (2000). An On-line Public Auc-
tion Protocol Protecting Bidder Privacy, in Proceed-
ings of ACSIP 2000 - Australasian Conference on In-
formation Security and Privacy, vol. 1841 of Lecture
Notes in Computer Science, Springer-Verlag, 427-
442.
Omote, K. and Miyaji, A. (2001). A Practical English Auc-
tion with One-Time Registration, in Proceedings of
ACSIP 2001 - Australasian Conference on Informa-
tion Security and Privacy, vol. 2119 of Lecture Notes
in Computer Science, Springer-Verlag, 221-234.
Stubblebine, S. and Syverson, P. (1999). Fair On-line Auc-
tions Without Special Trusted Parties, in Proceed-
ings of Financial Cryptography 1999, vol. 1648 of
Lecture Notes in Computer Science, Springer-Verlag,
230-240.
Tsudik, G. and Xu, S. (2003). Accumulating Composites
and Improved Group Signing, in Advances in Cryptol-
ogy - Proceedings of ASIACRYPT 2003, vol. 2894 of
Lecture Notes in Computer Science, Springer-Verlag,
269-286.
Trevathan, J. (2005). Security, Anonymity and Trust in
Electronic Auctions, Association for Computing Ma-
chinery Crossroads, Spring Edition, 3-9, vol. 11.3.
Trevathan, J., Ghodosi, H. and Read, W. (2005). Design
Issues for Electronic Auctions, in 2nd International
Conference on E-Business and Telecommunication
Networks, 340-347.
Trevathan, J., Ghodosi, H. and Read, W. (2006). An
Anonymous and Secure Continuous Double Auction
Scheme, in 39th International Hawaii Conference on
System Sciences, 125(1-12).
Viswanathan, K., Boyd, C. and Dawson, E. (2000). A
Three Phased Schema for Sealed Bid Auction System
Design, Proceedings of ACSIP 2000 - Australasian
Conference on Information Security and Privacy, vol.
1841 of Lecture Notes in Computer Science, Springer-
Verlag, 412-426.
SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY
396
