A HYBRID CLUSTERING CRITERION FOR R*-TREE

ON BUSINESS DATA

Yaokai Feng, Zhibin Wang, Akifumi Makinouchi

The Graduate School of Information Science and Electrical Engineering, Kyushu University, Japan

Keywords: Multidimensional indices, R*-tree, clustering

criterion, Multidimensional range query, TPC-H.

Abstract: It is well-known that multidimensional indices are efficient to improve the query performance on relational

data. As one successful multi-dimensional index structure, R*-tree, a famous member of the R-tree family,

is very popular. The clustering pattern of the objects (i.e., tuples in relational tables) among R*-tree leaf

nodes is one of the deceive factors on performance of range queries, a popular kind of queries on business

data. Then, how is the clustering pattern formed? In this paper, we point out that the insert algorithm of R*-

tree, especially, its clustering criterion of choosing subtrees for new coming objects, determines the

clustering pattern of the tuples among the leaf nodes. According to our discussion and observations, it

becomes clear that the present clustering criterion of R*-tree can not lead to a good clustering pattern of

tuples when R*-tree is applied to business data, which greatly degrades query performance. After that, a

hybrid clustering criterion for the insert algorithm of R*-tree is introduced. Our discussion and experiments

indicate that query performance of R*-tree on business data is improved clearly by the hybrid criterion.

1 INTRODUCTION

More and more applications need processing

multidimensional range queries on business data

usually stored in relational tables. For example,

Relational On-Line Analytical Processing in data

warehouse is required to answer complex and

various types of range queries on large amount of

such data. In order to obtain good performance for

such multidimensional range queries, multi-

dimensional indices are helpful (V. Markl and Bayer,

1999a; V. Markl and Bayer, 1999b), in which the

tuples are clustered among the leaf nodes to restrict

the nodes to be accessed for queries.

So many index structures exist. Among them,

-tree (Beckmann and Kriegel, 1990) is one of the

well-known and successful ones, and widely used in

many applications and researches (C. Chung and

Lee, 2001; D. Papadias and Delis, 1998; H.

Horinokuchi and Makinouchi, 1999; H. P. Kriegel

and Schneider, 1993; Jurgens and Lenz, 1998). R*-

tree is also used in this study. Anyway, we want to

note that our proposal in this study can also be used

to other hierarchical index structures, including the

other members of R-tree family.

In the works (C. Chung and Lee, 2001; Kotidis

and

N. Roussopoulos, 1998; Jurgens and Lenz 1998;

N. Roussopoulos and Y. Kotidis, 1997; S. Hon and

Lee, 2001), the aggregate values are pre-computed

and stored in a multidimensional index as

materialized view. When required, the aggregate

values can be retrieved efficiently. In this study, we

also use a multidimensional index for relational data.

However, it is completely different from the related

works in that our study focuses on enhancing R*-

tree to speed up evaluation of range queries

themselves.

In this paper, it is pointed out that the clustering

pat

tern of tuples among the leaf nodes is a decisive

factor on search performance. But, there exist many

very slender leaf nodes when R*-tree is used to

index business data, which greatly degrades query

performance. Slender nodes mean the nodes whose

MBRs (Minimum Bounding Rectangle) have at least

one very narrow side (even the side length is zero) in

some dimension(s). Clearly, slender nodes have very

small, even 0, areas (volumes in 3 or more

dimensional spaces. Note that, area and volume are

used interchangeably in this paper). Some examples

are those MBRs roughly shaped as line segments in

2-dimensional spaces and roughly shaped as plane or

line segments in 3-dimensional spaces.

According to our discussion in this paper, the

reaso

n of so many slender leaf nodes existing

becomes clear. The insert algorithm of R*-tree,

especially, its criterion (called clustering criterion)

346

Feng Y., Wang Z. and Makinouchi A. (2005).

A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 346-352

DOI: 10.5220/0002552703460352

 SciTePress

of choosing subtrees for new coming tuples,

determines the clustering pattern of tuples among the

leaf nodes. After that, we make it clear that the

present clustering criterion in the insert algorithm of

R*-tree is not suitable to R*-tree applied to business

data. Instead, a hybrid clustering criterion is

proposed. Our discussion and experiment indicate

that query performance of R*-tree on business data

is improved much by the new clustering creation.

The rest of the paper is organized as follows.

Section 2 describes how to use multidimensional

indices for relational data. Section 3 presents our

observations when R*-tree is used to business data

and the reason of our observations is discussed in

detail. Section 4 is our proposal: a hybrid clustering

criterion for R*-tree. Section 5 gives experimental

result, and Section 6 concludes the paper.

2 INDEXING BUSINESS DATA

USING R*-TREE

In this section, let us see how to use R*-tree to

business data and give some terms. Due to the

limitation of pages, R*-tree is not introduced in this

paper. Readers can refer the works (Beckmann and

Kriegel, 1990, Y. Feng, A. Makinouchi and H. Ryu,

2004).

Let T be a relational table with n attributes,

denoted by T(A1, A2, …, An). Attribute Ai (1 ≤ i ≤

n) has domain D(Ai), a set of possible values for Ai.

The attributes often have types such as Boolean,

integer, floating, character string, date, and so on.

Each tuple t in T is denoted by <a1,a2, … ,an>,

where ai (1 ≤ i ≤ n) is an element of D(Ai).

When R*-tree is used in relational tables, some

of the attributes are usually chosen as index

attributes, which are used to build R*-tree. For

simplification of description, it is supposed without

loss of generality that the first k (1≤ k ≤ n) attributes

of T, <A1,A2, … ,Ak>, are chosen as index

attributes. Since R*-tree can only deal with numeric

data, an order-preserving transformation is necessary

for each non-numeric index attributes. After

necessary transformations, the k index attributes

form a k-dimensional space, called index space,

where each tuple of T corresponds to one point.

It is not difficult to find such a mapping

function for Boolean attributes and date attributes (Y.

Feng, A. Makinouchi and H. Ryu, 2004). The work

(H. V.Jagadish and Srivastava, 2000) proposes an

efficient approach that maps character strings to real

numeric values within [0,1], where the mapping

preserves the lexicographic order. This approach is

also used in this study to deal with attributes of

character string.

We call the value range of Ai, [li, ui] (1≤ i ≤ k)

data range of Ai, an index attribute (in this paper,

“dimension” and “index attribute” are used

interchangeably). The length of the data range of Ai,

|ui-li|, is denoted by R(Ai). The k-dimensional

hyper-rectangle, [l1,u1]× [l2,u2]×…×[lk, uk], forms

the index space. Attributes specified in the range

query condition is called query attributes.

If R*-tree is used to index business data stored

in a relational table, all the tuples are clustered in

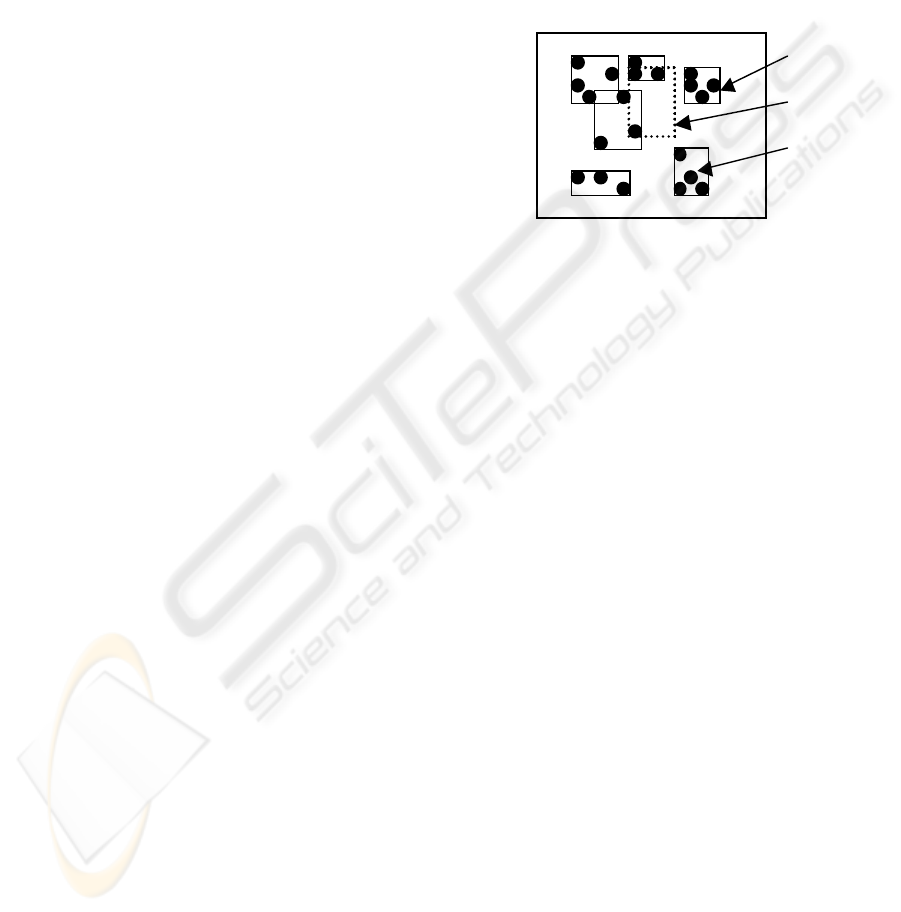
R*-tree leaf nodes. See Figure 1.

leaf nodes

query range

Figure 1. Leaf nodes and query range.

tuple

Figure 1: Leaf nodes and query range

Figure 1 shows an example of leaf nodes and query

range. Query range, given by user, refers to the

region, where the user wants to find the result.

Clearly, from Figure 1, if the tuples are properly

clustered among the leaf nodes, the number of leaf

nodes to be accessed for this range query will drop.

Thus, the clustering pattern is a deceive factor on

query performance. The question is that who decides

the clustering pattern? The answer is “clustering

criterion” in the insert algorithm of R*-tree.

R*-tree is constructed by inserting the objects

one by one. In constructing procedure, the insert

algorithm has to choose a proper subtree to contain

each new-coming tuple. The criterion that decides

which subtree should be chosen is called insert

criterion or clustering criterion in this paper. Of

course, for a given dataset, this criterion decides the

final clustering pattern of the tuples among leaf

nodes. In this paper, it will be pointed out that the

present clustering criterion of R*-tree cannot lead to

a proper clustering pattern when R*-tree is used to

business data. And a novel clustering criterion will

be proposed.

3 OBSERVATIONS AND OUR

EXPLANATION

In this section is our observations on R*-tree used

for business data. And, the observations are also

explained.

A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA

347

3.1 Observations

Just as pointed out in our other work (Y. Feng, A.

Makinouchi and H. Ryu, 2004), because of the

particularity of business data, some new features

occur when R*-tree is used to index business data.

As a feature of business data, the data ranges of

attributes are very different from each other. For

instance, the data range of “Year” from 1990 to

2003 is only 13 while the amount of “Sales” for

different “Product” may be up to several hundreds of

thousands.

Another typical example of such attributes with

small cardinalities is Boolean attribute, which has

inherently only two possible values. Attributes with

other data type may also semantically have small

cardinality (e.g., “Weekday” with seven values). In

LINEITEM table of TPC-H benchmark,

RETURNFLAG, SHIPINSTRUCT, and

SHIPMODE have only 3, 4, and 7 distinct values,

respectively, although their data type is character

string.

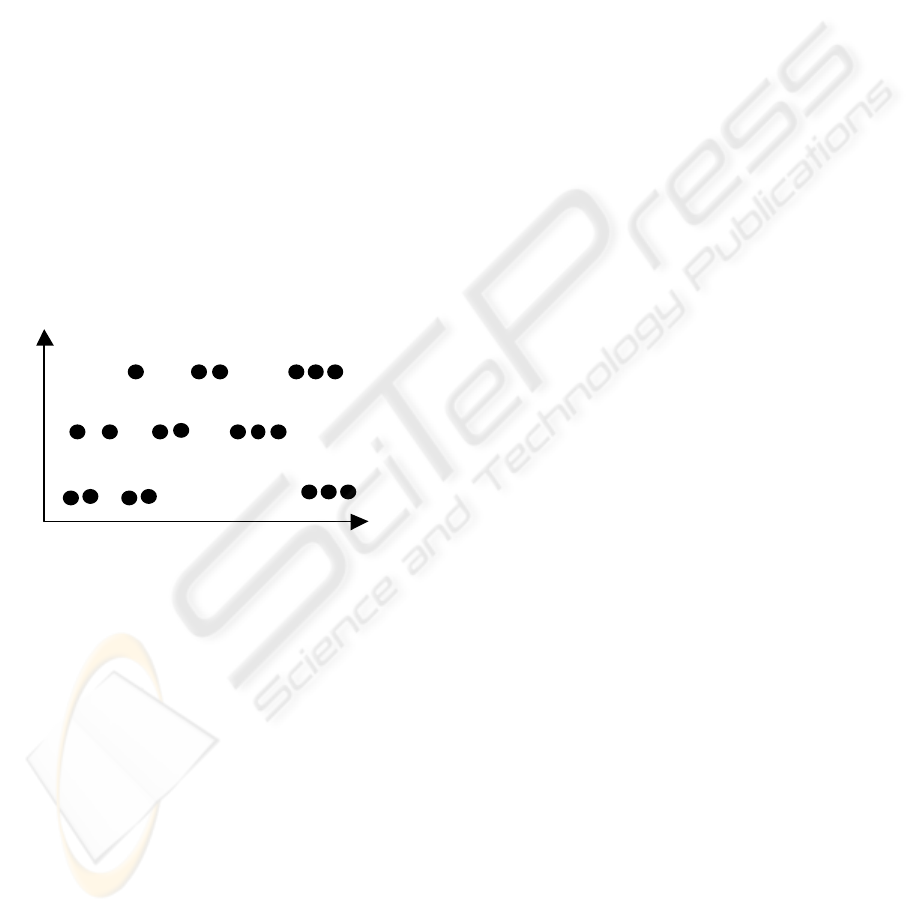
Figure 2 shows an example in 2-dimensional

space.

x-axis (floating value)

y-axis (3 values)

Figure 2. Tuples in index space.

In Figure 2, y-axis has only 3 different values. On

the contrary, x-axis type is floating and has many

possible values. Thus, the tuples (black dots) are

distributed in lines.

In order to investigate the slender nodes in R*-tree

used in business data, using the LINEITEM table in

TPC-H benchmark, an R*-tree was constructed and

all the areas (or say volumes) of the leaf nodes are

computed. Totally 200,000 tuples are generated in

this table having 16 attributes. Six attributes,

SHIPDATE (date), QUANTITY (floating),

DISCOUNT (floating), SHIPMODE (character

string), SHIP-INSTRUCT (character string), and

RETURNFLAG (character string), are selected as

index attributes since they are often used as query

attributes in the queries of the benchmark. The page

size of our system is 4KB and each leaf node can

contain at most 77 tuples. The R*-tree has 4 levels

with 4649 leaf nodes. We observe that, 2930 of these

4649 leaf nodes have 0-area. Over 60%! And, there

are still many leaf nodes have only very-small areas.

We also use 200,000 6-dimensional synthetic

data with Zipf distribution to investigate existing of

slender nodes. The observation is very similar. Zipf

distribution is often used in the researches related to

business data (S. Hong, B. Song and S. Lee. 2001).

Certainly, the basic reason that slender nodes

exist is he distribution of tuples in the index space.

3.2 The Existing Clustering Criterion

in R*-tree

Since the clustering criterion is so important on the

clustering pattern of tuples among leaf nodes of R*-

tree (which is one of deceive factors on query

performance) and this study tries to introduce a new

clustering criterion, let us briefly recall the present

clustering criterion of R*-tree as follows.

A new-coming tuple will be inserted in the

node (subtree) at the current level with

1) (for leaf level) the least enlargement of overlap

area, if tie occurs then

2) the least enlargement of MBR area, if tie occurs

again then

3) the least MBR area.

This criterion means that, if the new tuple

reaches at the leaf level, the new-coming tuple is

tried to enter each node and the enlargement of

overlap area in each case among the leaf nodes is

calculated. And the node with the least enlargement

of overlap area is chosen to contain the new-coming

tuple. If several nodes have the least enlargement

then, the enlargement of MBR area in each case is

calculated and the node with the least enlargement

of MBR area is chosen. If tie occurs again then the

node with the smallest MBR area is chosen. If tie

still occurs, then arbitrary one of those nodes with

the smallest MBR area is chosen. For the

intermediate level, the area enlargement of overlap

among the nodes is not calculated and only (2) and

(3) in the criterion are used.

Figure 2: Tuples index space

In the next subsection, we will know that the

existing of slender leaf nodes is a “positive

feedback”. That is, once some slender leaf nodes

exist, they will become more and more as the new

tuples are inserted, which greatly deteriorates search

performance.

3.3 Positive Feedback

Let us consider the insertion algorithm of R*-tree,

using the example depicted in Figure 3 (a). Node A

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

348

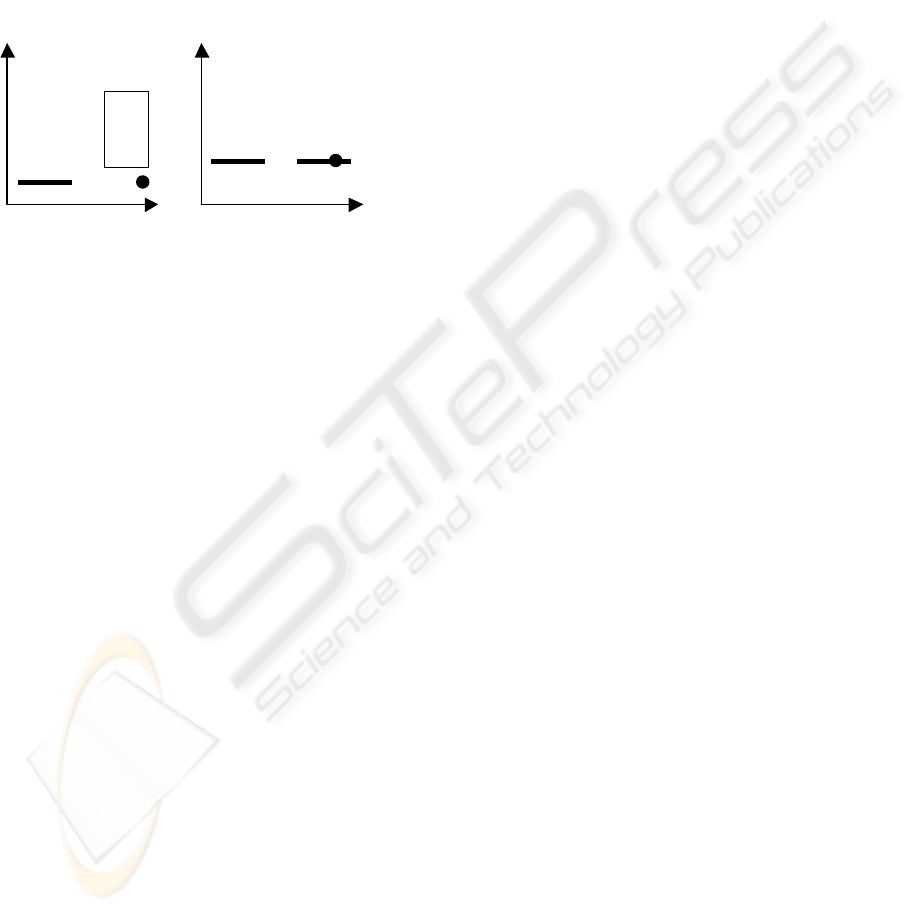
is a slender node and point p is to be newly inserted.

Certainly it should be inserted in Node B since it is

so nearer to Node B than to Node A. However,

according to the insert algorithm of R*-tree, p will

be inserted to Node A in this case. This is because

the area increment of doing so is smaller than that of

inserting p to Node B. Even if the enlargement of

overlap area among the nodes at this level is

considered, Node A also tends to be chosen. After p

is inserted Node A, Node A becomes very long,

which may deteriorate the overlap between Node A

and the other nodes.

Node A

Node B

Node A Node B

(a) (b)

Figure 3. Slender nodes exist.

Let us to see another case shown in Figure 3 (b).

There are two MBRs shaped as line segments, A and

B. Let assume p is a new tuple to be inserted. Where

should it go? Intuitively, p should be included in

Node B. Actually, p may be inserted in Node A,

although this enlarges the overlap (between A and

B) and also leads to a long node A. This is because

the insertion algorithm of R*-tree cannot determine

which node, A or B, should be selected since both

overlap area increment and area increment of

selecting A and selecting B are 0. As a result, either

Node A or Node B is selected as default without

consideration of actual overlap. Here, we assume

that without loss of generality Node A is selected.

Same as the previous case, after p is inserted Node A,

Node A becomes very long, which may deteriorate

the overlap between Node A and the other nodes.

And, when a new point (tuple) with the same y-axis

coordinate as p is inserted again, the same process is

repeated and the new point is also inserted into Node

In this way, the new-coming tuples tend to be

inserted into the existing slender nodes and the

repeated insertions of such tuples lead to the

overflow of slender nodes and the slender nodes are

split again and again. As a result,

1) many slender nodes are generated,

2) the space utilization of such nodes degrades

much and the total number of nodes in R*-tree

tends to increase,

3) very slender nodes tend to be very long (there is

a low band on the number of tuples in each leaf

node),

4) overlapping among the leaf nodes is very heavy,

which greatly destroy search performance. This

study does not aim at eliminating the existing of

slender nodes since its existing, basically speaking,

is from the distribution of tuples (as mentioned

above). The main purpose of this study is to

decrease the overlap among leaf nodes by making

the clustering pattern more proper and reasonable.

At the same time, the number of slender nodes is

also decreased and the total space utilization of

nodes also can be improved.

4 A HYBRID CLUSTERING

CRITERION

Generally speaking, the present clustering criterion

(mentioned above) of R*-tree is based on area,

including overlap area enlargement, MBR area

enlargement, and MBR area, which leads to many

slender nodes and very heavy overlap among the

leaf nodes. In this section, we explain how to deal

with the problem of slender nodes by a hybrid

clustering criterion.

Figure 3: Slender nodes exist

Our approach to this problem includes the

following two points.

(1) Modifying the area calculation.

Why a proper subtree or a leaf node can not be

found for new-coming tuples? The reason is that the

enlargements both on overlap area and on MBR area

are zero for 0-area nodes. Thus, comparison can not

be made reasonably among inserting the tuples to

the existing nodes.

In order to avoid this situation, we modified the

area calculation. That is, when the area of a

rectangle, a node MBR or the overlap region of two

node MBRs, is calculated, all the zero-sides (i.e., the

side length is zero), if exist, of this rectangle is set to

a trivial non-zero positive value (e.g., 10

-4

in our

experiments).

Let us recall the original area calculation of

rectangle R as follows.

,)(

∏

SRArea

where S

is the side length of R in dimension i. d is

dimensionality of the index space.

In this study, this area calculation is modified as

follows.

A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA

349

⎩

⎨

⎧

=−

′

∏

,)(

otherwiseS

Svaluetrivial

SRaAre

where the trivial-value is set to 10

-4

in this paper.

Anyway, this trivial value must be less than the unit

in this attribute to avoid confusing. In the same time,

the trivial-value should not be too small, or the

calculation result cannot be expressed. These two

conditions are not difficult to be guaranteed in real

applications. In this way, most of un-comparable

situations caused by 0-area nodes can be avoided.

Note that, this modification only changes the

clustering pattern of tuples among the leaf nodes and

it has no effect on the correctness of the query result.

(2) Introducing a distance-criterion.

If the above area-criterion still cannot decide

which subtree or leaf node is most suitable to one

new-coming tuple, which means the area-based

clustering criterion is no longer in force, the nearest

subtree or leaf node to the new-coming tuple is

chosen.

Summarily speaking, the hybrid clustering criterion

combines the modified area-based one with a

distance-based one. The procedure is as follows.

1) For leaf level, compare the enlargements of

overlap areas using the modified calculation. If

tie then

2) Compare the enlargements of MBR areas using

the modified calculation. If tie then

3) Choose the nearest subtree (a leaf node for leaf

level).

Now, let us see how to calculate the distance from

one point to a rectangle region.

For a point p= (p

, …, p

) and a rectangle R.

Let the points s= (s

, …, s

) and t = (t

, …, t

) be the

two vertices of the node MBR with the minimum

coordinates and maximum coordinates in each axis,

respectively. The distance from p to R, dist(p, R),

can be given by

⎪

⎩

⎪

⎨

⎧

otherwisep

tpt

sps

where

iii

−=

∑

,),(

rpRpdist

5 EXPERIMENTS

Using the TPC-H data (Council, 1999), we

performed various experiments to show how much

the range query performance is improved using the

hybrid clustering criterion.

Dataset and index attributes: Lineitem table of

TPC-H benchmark, which has 16 attributes of

various data types including floating, integer, date,

string, Boolean. The table used in our experiments

has 200,000 tuples. Six of the total 16 attributes are

chosen as index attributes, including SHIPDATE

(date), QUANTITY (floating), DISCOUNT

(floating), SHIPMODE (character string),

SHIPINSTRUCT (character string), and

RETURNFLAG (character string), since they are

often used as query attributes in the queries of the

benchmark.

System: the page size in our system is 4KB and

all the index structures are built based on “one node

one page”.

Queries: the query ranges of QUANTITY

(floating) and DISCOUNT (floating) both are

changed from 10% to 100%. As for the date attribute

of SHIPDATE (date), the query range is the period

of one year and it is selected randomly for each

query. As for the other 3 attributes (character string),

since their numbers of possibly different values are

only 3, 4, and 7, respectively. One value is chosen

randomly in each of the 3 attributes. Each query is

repeated 100 times for different location and the

average numbers of accessed different nodes are

presented. The average number of node accesses is a

common criterion for evaluating query performance

(H. V. Jagadish and Srivastava, 2000).

5.1 Effect of the Hybrid Clustering

Criterion on R*-tree

In order to know effect of the new clustering

criterion on R*-tree itself, the total numbers of nodes

in R*-trees with different clustering criterions and

the result is present in Table 1, where M refers to the

upper bound on the number tuples contained in each

leaf node of R*-tree.

Table 1: R*-tree with different clustering criterion.

R*-tree with

original clustering

criterion

R*-tree with

hybrid clustering

criterion

M 77 77

Height 4 4

Total

number

of nodes

4892 3783

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

350

From Table 1, we can know that the hybrid

clustering criterion make R*-tree more compact.

5.2 Effect of the Hybrid Clustering

Criterion on Query Performance

Table 2: Comparison on the number of accessed different

nodes

Query

range

R*-tree with

original

clustering criterion

R*-tree with

hybrid

clustering criterion

10% 369.91 95.12

20% 648.90 126.33

30% 603.65 131.31

40% 388.67 137.30

50% 683.29 237.27

60% 489.00 248.10

70% 708.24 231.10

80% 691.89 275.48

90% 571.10 357.62

100% 764.55 358.49

The result of comparison on the number of accessed

different nodes is included in Table 2.

From Table 2, we can know that the hybrid

clustering criterion can greatly improve the query

performance. Anyway, note that,

(1) In Table 2, the first column, query range, refers

to the side length of the query range in the two

floating attributes, i.e., QUANTITY and

DISCOUNT. The query with same size of query

range in the floating attributes is repeated 100 times

with different locations (randomly). However, this

query range is not relevant to the other index

attributes, which is explained before.

(2) According to Table 2, the number of accessed

different nodes is not always increase as the “query

range” in the first column grows. This is because

that the query ranges in the other 4 index attributes

change randomly at the same time when the query

ranges in the two floating attributes grow.

Moreover, the CPU time cost is also tested and

compared, which is presented in Table 3.

From Table 3, we can observe that the hybrid

clustering criterion also lead to a shorter CPU time,

which means that it is effective even for main-

memory-resident R*-tree, where the I/O is no long

the bottleneck of the query performance. Note that,

our OS is FreeBSD 4.9 and main memory is 128MB.

Table 3: Comparison on CPU time (ms)

Query

range

R*-tree with

original

clustering criterion

R*-tree with

hybrid

clustering criterion

10% 16.401 5.939

20% 28.180 8.117

30% 26.582 8.499

40% 17.780 9.074

50% 33.137 15.817

60% 25.103 16.769

70% 33.940 15.874

80% 34.420 19.101

90% 32.721 24.772

100% 41.671 25.751

6 CONCLUSIONS

It is important to process various types of range

queries on business data. R*-tree is one of the

successful multidimensional index structures and is

also helpful to improve query performance on

business data. In this paper, we pointed out that

many slender nodes, including many 0-area nodes,

exist if R*-tree is applied to business data, which

greatly degrade query performance. The reason that

many slender nodes occur was made clear in this

paper and a hybrid clustering criterion is introduced

to deal with the problem of slender nodes.

According to our discussion, the hybrid clustering

criterion can improve the clustering pattern of tuples

among leaf nodes, especially it can decrease the

overlap among the leaf nodes. And our approach

clearly improved query performance of R*-tree in

our experiments.

ACKNOWLEDGEMENT

This research is partially supported by Japan Society

for the Promotion of Science, Grant-in-Aid for

Scientific Research 15650017 and 16200005.

REFERENCES

C. Chung, S. Chun, J. Lee, and S. Lee (2001). Dynamic

Update Cube for Range-Sum Queries. Proc. VLDB

Intl. Conf.,

Council (1999). TPC benchmark H standard specification

(decision support)".

http://www.tpc.org/tpch/

D. Papadias, N. Mamoulis, and V. Delis (1998).

Algorithms for Querying by Spatial Structure. Proc.

VLDB Intl. Conf.

A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA

351

H. Horinokuchi, and A. Makinouchi (1999). Normalized

R*-tree for Spatiotemporal Databases and Its

Performance Tests. IPSJ Journal, Vol. 40, No. 3.

H. P. Kriegel, T. Brinkhoff, and R. Schneider (1993).

Efficient Spatial Query Processing in Geographic

Database Systems.

H. V. Jagadish, N.Koudas, and D. Srivastava (2000). On

Effective Multi-Dimensional Indexing for Strings.

Proc. ACM SIGMOD Intl. Conf.

J. Han and M. Kamber (2001). Data Mining—Concepts

and Techniques. Morgan Kaufmann press.

M. Jurgens, and H.-J. Lenz (1998). The Ra*-tree: An

Improved R-tree with Materialized Data for

Supporting Range Queries on OLAP-Data. Proc.

DEXA Workshop.

N. Beckmann, and H. Kriegel (1990). The R*-tree: An

Efficient and Robust Access Method for Points and

Rectangles. Proc. ACM SIGMOD Intl. Conf.

N. Roussopoulos, S.K and F. Vincent (1995). Nearest

neighbor Query. Proc. ACM SIGMOD Intl. Conf.

N. Roussopoulos, Y. K and M. Roussopoulos (1997).

Cubetree: Organizaiton of and Bulk Incremental

Updates on the Data Cube. Proc. ACM SIGMOD Intl.

Conf.

R. Agrawal, A. Gupta, and S. Sarawagi (1997).

ModelingMultidimesnional Databases. Proc. Intl. Conf.

on Data Engineering (ICDE).

S. Hon, B. Song, and S. Lee (2001). Efficient Execution of

Range-Aggregate Queries in Data Warehouse

Environments. Proc. the 20th Intl. Conf. on

conceptual modeling.

S. Hong, B. Song and S. Lee (2001). Efficient Execution

of Range-Aggregate Queries in Data Warehouse

Environments, Proc. 20th

international Conference on

CONCEPTUAL MODELING (ER 2001).

V. Markl, F. Ramsak, and R. Bayer (1999a). Improving

OLAP Performance by Multidimensional Hierarchical

Clustering. Proc. IDEAS Intl. Synposium.

V. Markl, M. Zirkel, and R. Bayer (1999b). Processing

Operations with Restrictions in Relational Database

Management Systems without external Sorting. Proc.

Intl. Conf. on Data Engineering.

Y. Feng, A. Makinouchi, and H. Ryu (2004). Improving

Query Performance on OLAP-Data Using Enhanced

Multidimensional Indices. Proc. ICEIS Intl. Conf.

Y. Kotidis, and N. Roussopoulos (1998). An Alternative

Storage Organization for ROLAP Aggregate Views

Based on Cubetrees. Proc. ACM SIGMOD Intl. Conf.

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

352