OPTIMAL TRADE-OFF FOR MERKLE TREE TRAVERSAL

Marek Karpinski

∗

Dept. of Computer Science

University of Bonn

Yakov Nekrich

†

Dept. of Computer Science

University of Bonn

Keywords:

Identiﬁcation and Authentication, Merkle Trees, Public Key Signatures, Authentication Path, Fractal Tree

Traversal, Trade-off, Amortization.

Abstract:

In this paper we describe optimal trade-offs between time and space complexity of Merkle tree traversals

with their associated authentication paths, improving on the previous results of Jakobsson, Leighton, Micali,

and Szydlo (Jakobsson et al., 03) and Szydlo (Szydlo, 04). In particular, we show that our algorithm requires

2 log n/ log

(3)

n hash function computations and storage for less than (log n/ log

(3)

n+1) log log n+2 log n

hash values, where n is the number of leaves in the Merkle tree. We also prove that these trade-offs are optimal,

i.e. there is no algorithm that requires less than O(log n/ log t) time and less than O(t log n/ log t) space for

any choice of parameter t ≥ 2.

Our algorithm could be of special use in the case when both time and space are limited.

1 INTRODUCTION

Merkle trees have found wide applications in cryp-

tography mainly due to their conceptual simplicity

and applicability. Merkle trees were ﬁrst described by

Merkle (Merkle, 82) in 1979 and studied intensively.

In cryptographic applications, however, Merkle trees

were not very useful for small computational devices,

as the best known techniques for traversal required a

relatively large amount of computation and storage.

Several recent papers, e.g., (Jakobsson et al., 03) and

(Szydlo, 04), improved the time and space complex-

ity of Merkle trees. In this paper we address the issue

of possible further improvements of Merkle tree tra-

versals.

Merkle tree is a complete binary tree such that val-

ues of internal nodes are one-way functions of the val-

ues of their children. Every leaf value in a Merkle tree

can be identiﬁed with respect to a publicly known root

and the authentication path of that leaf. An authen-

tication path of a leaf consists of the siblings of all

nodes on the path from this leaf to the root.

∗

Work partially supported by DFG grants , Max-Planck

Research Prize, DIMACS and IST grant 14036 (RAND-

APX).

†

Work partially supported by IST grant 14036 (RAND-

APX).

Merkle trees have many cryptographic applica-

tions, such as certiﬁcation refreshal (Micali, 97),

broadcast authentication protocols (Perrig et al., 02),

third party data publishing (Devanbu et al., 01),

zero-knowledge sets (Micali et al., 03) and micro-

payments (Rivest, Shamir, 96). A frequent prob-

lem faced in such applications is the Merkle tree tra-

versal problem, the problem of consecutively out-

putting the authentication data for every leaf. In

(Merkle, 87) Merkle has proposed a technique for

traversal of Merkle trees which requires O(log

space and O(log n) time per authentication path in

the worst case. Recently, two results improving a

technique of Merkle have appeared. In (Jakobsson

et al., 03) the authors describe a Merkle tree tra-

versal algorithm with O(log

n/ log log n) space and

O(log n/ log log n) time per output. In (Szydlo, 04)

Szydlo describes a method requiring O(log n) space

and O(log n) time and provides a proof that this

bound is optimal, i.e. he proves that there is no traver-

sal algorithm that would require both o(log n) space

and o(log n) time. Observe that we measure the time

complexity of outputting the authentication path of a

single leaf.

In this paper we investigate further the trade-off be-

tween time and space requirements of Merkle tree tra-

versals.

275

Karpinski M. and Nekrichâ

a Y. (2005).

OPTIMAL TRADE-OFF FOR MERKLE TREE TRAVERSAL.

In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 275-282

DOI: 10.5220/0001414202750282

 SciTePress

First, we present an algorithm that works in

O(log n/h) time and

O((log n/h)2

) space per round for arbitrary para-

meter h ≥ 1. For h = O(1) our result is equivalent

to the result of Szydlo; however, we consider all op-

erations (not just computations of one-way functions)

in our analysis. Our result is also an extension of that

of Jakobsson, Leighton, Micali and Szydlo (Jakobs-

son et al., 03); we prove that it can be extended for

arbitrary values of h.

Secondly, we show that the results of Szydlo

and Jakobsson, Leighton, Micali, Szydlo remain

true, if we consider all operations and not just

hash computations. (If h is not a constant,

we ignore time that we need to output the val-

ues in the last case). In particular, we show

that an algorithm with 2 log n/ log log log n hash

functions evaluations and storage requirement of

(log n/ log log log n + 1) log log n + 2 log n hash val-

ues per output can be constructed. This algorithm

works with O(log n/ log

(3)

n) operations per output.

At the end, we show that if a tree traversal algo-

rithm works in time O(log n/h), then required space

is Ω((log n/h)2

). Thus we show that our trade-off

is optimal.

The presented results give a complete answer to the

question of time and space complexity of the Merkle

tree traversal problem. These results are also impor-

tant for practical applications.

2 PRELIMINARIES AND

NOTATION

Below we denote by a hash a one-way function, and

hash computation will denote a computation of the

value of a one-way function. In a Merkle tree leaf

values are hash values of leaf pre-images. Leaf pre-

images can be, for instance, generated with a pseudo-

random generator. We will denote by leaf-calc a

function that computes pre-images of the leaves.

Let φ

=hash◦leaf-calc be the function that computes

value of the i-th leaf. Let φ

(parent)=hash(left-

child||right-child) be the function that computes the

value of the parent node from the values of its chil-

dren. We will presume that we need one computation

unit to compute φ

or φ

We must generate n outputs, where n is the num-

ber of leaves. Every output consists of the leaf pre-

image and its authentication path. An authentication

path consists of the siblings of all nodes on the path

to the root. Outputs for the leaves must be gener-

ated consecutively left-to-right. This makes our task

easier, because outputs for consecutive leaves share

many common node values.

In order to verify a leaf, one consecutively com-

putes the values of its ancestors. Veriﬁcation succeeds

only if the computed root value equals to the known

root value.

In this paper the following notation will be used. H

will denote the Merkle tree height. We will say that a

node is on level A, if its depth is H −A. The i-th node

from the left on level A will be denoted by (A, i). A

job, computing node (A, i) will also be denoted by

(A, i). We will say that A is the job level and i is the

index of the job. Sometimes we will identify a subtree

of the Merkle tree by its root node (A, i). We will

use a subtree height h as a parameter in our algorithm

and L will be equal to H /h. We say that a node N is

needed if it is a part of an authentication path.

3 MAIN IDEA

We describe here the main idea of our algorithm and

key observations on which the algorithm is based.

The well-known evaluation algorithm, shown on

Fig. 1, is used to compute the value of the i-th node

on level A and is an important part of all Merkle tree

traversal algorithms.

Eval (A,i)

if (A == 0)

return φ

(i);

else

minlev := A − 1

V := Eval(A − 1, 2i)

V := φ

(V, Eval(A − 1, 2i + 1))

minlev := A

return V

Figure 1: Evaluation of the i-th node on level A

This basic version of algorithm Eval requires

O(2

) computational units and A storage units. The

last follows from the fact that at most one node value

V for every height i = 0, 1, . . . , A has to be stored at

every stage of the algorithm. These stored values will

be further called tail values. Variable minlev stores

the value of the minimal level and equals to the min-

imum level for which the tail value of a job must be

stored.

Our algorithm uses procedure Eval to estimate

the values of nodes that will be needed in the fu-

ture authentication paths. The set of computations

for ﬁnding the value of node (A, i) using procedure

Eval(A, i) will be further called a job (A, i).

Our algorithm combines two important observa-

tions that were also used in the papers of Jakobsson,

Leighton, Micali and Szydlo (Jakobsson et al., 03),

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

276

and Szydlo (Szydlo, 04). The ﬁrst key observation

on which our algorithm is based is that during the

computation of node (A, i) its children (A − 1, 2i),

(A − 1, 2i + 1) as well as all other descendants are

computed. Therefore by storing intermediate results

of evaluation some future computations can be saved.

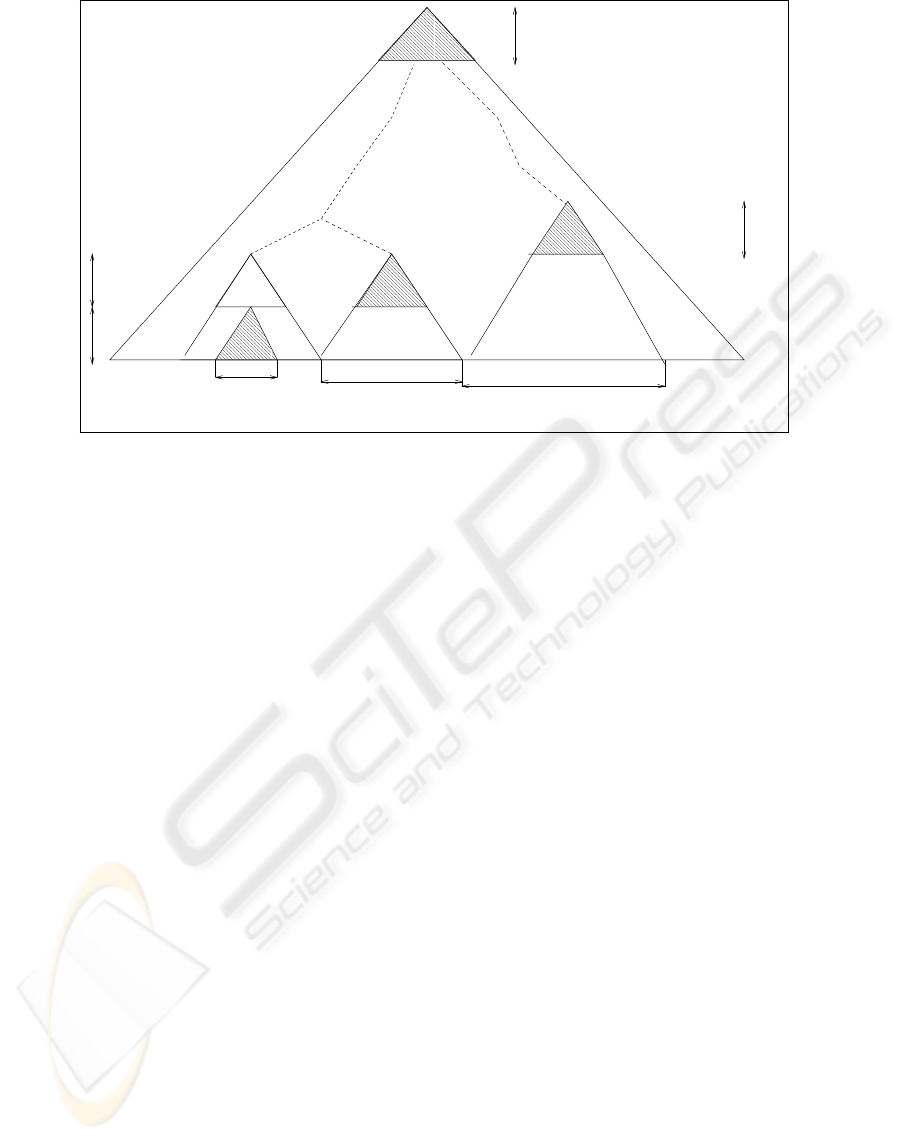
Actually, for every computed node N on level ih all

its descendants on levels ih − 1, . . . , ih − h (i.e. a

complete subtree of height h rooted in N) will be re-

tained to be used in the future authentication paths.

Thus only nodes at height ih, i = 1, . . . , L will be

computed directly (see Fig 2).

Another key observation is that we can schedule

the computations of the nodes needed in the future in

such a way that at most H storage units are necessary

to store all tail values.

In section 6 a further constant improvement is de-

scribed. We show that in a subtree only nodes with

odd indices must be stored. We also show that the

next subtree can be computed as the nodes of the cur-

rent subtree are discarded so that the total number of

nodes used by subtrees on a level is 2

4 ALGORITHM DESCRIPTION

Our algorithm consists of three phases: root genera-

tion, output, and veriﬁcation. During the ﬁrst phase

the root of the Merkle tree is generated. Addition-

ally, the initial set of subtrees with roots at (0, 2

i = 1, . . . , L is computed and stored. The veriﬁcation

phase is identical to the traditional veriﬁcation phase

(see, for instance, (Jakobsson et al., 03)). The output

phase consists of 2

rounds, and during round j an

image of the j-th leaf and its authentication path are

output. In the rest of this section we will describe an

algorithm for the output phase and prove its correct-

ness.

For convenience we will measure time in rounds.

During each round 2L computation units are spent on

computation of subtrees needed in the future authen-

tication paths. Thus our algorithm starts at time 0 and

ends at time 2

− 1, and the i-th round starts at time

i. In the ﬁrst part of the algorithm description we will

ignore the costs of all operations, except of the com-

putations of hash functions. Later we will show that

the number of other operations performed during a

round is O(L).

During round j we store L already computed sub-

trees with roots at (sh, m

) where j ∈ [m

, (m

1)2

), s = 0, 1, . . . , L. During the same round we

also spend 2L computation units in order to compute

jobs (sh, m

+ 1) and construct the corresponding

subtrees. At round (m

+ 1)2

the subtree (sh, m

)

will be discarded, However the subtree (sh, m

+ 1)

will be retained for the next 2

rounds, while subtree

(sh, m

+ 2) is computed.

During each round there are at most L different

jobs competing for 2L computation units. These jobs

will be called active. Active jobs are scheduled ac-

cording to the following rules:

1. A job (ih, k) k = 1, . . . , H/2

becomes active at

time (k −1)2

, i.e. during the (k −1)2

-th round.

2. All active jobs (s

′

, k

′

) with s

′

> s such that mini-

mal level of (s

′

, k

′

) does not exceed s have priority

over the job (s, k

) on level s.

3. In all other cases jobs with the lower level have pri-

ority over jobs with the higher level.

Consider job (sh, i) that becomes active at time

(i − 1). Rule 2 guarantees us that all jobs with

levels s

′

h such that s

′

> s do not store any tail val-

ues on levels 1, 2, . . . , sh − 1 when the computation

of job (sh, i) starts. Therefore, when job (sh, i) is

computed, only one tail node on each of the levels

(s − 1)h, (s − 1)h + 1, . . . , sh − 1 will be stored.

Now consider a job (s

′′

h, is

′′

) on level s

′′

h, s

′′

1, . . . , s − 1. If job (sh, i) stores a tail node on level

˜s < s

′′

, then (s

′′

h, is

′′

) is either already completed

(rule 3), or did not start yet (rule 2).

This scheduling guarantees us that at any time only

one tail value for a level i = 1, 2, . . . , H will be stored

by all jobs (sh, i). Only 2L subtrees (one currently

used and one currently computed for each level ih)

must be stored at each round, and subtrees require

(2H/h)(2

h+1

−1) space. Hence the memory require-

ment of our algorithm is O((2H/h)2

) + O(H) =

O((H/h)2

These considerations allow us to formulate the fol-

lowing trade-off between time and space complexity.

Theorem 1 Merkle tree can be traversed in time

O(H/h) with O((H/h)2

) storage units for any h ≥

Corollary 1 Merkle tree can be traversed in time

O(log n/ log

(3)

n) with

O(log n log log n/ log

(3)

n) storage units.

In the next subsections we will prove the algorithm

correctness by showing that all values are computed

on time, and we prove the time bound stated in the

theorem by analysis of the operations necessary for

the job scheduling.

4.1 Correctness Proof

In this section we show that job (sh, k) will be com-

pleted at time k2

Lemma 1 Suppose that at time (k − 1)2

for every

level i = h, 2h, . . . , (s−1)h, (s +1)h, . . . Lh there is

at most one unﬁnished job on level i. Then job (sh, k)

will be completed before k2

OPTIMAL TRADE-OFF FOR MERKLE TREE TRAVERSAL

277

2 2 2

h+1

h+2

Figure 2: Subtrees computed at a round of the algorithm

Proof: Consider the time interval [(k − 1)2

, k2

There is at most one job (s

′′

h, k

′′

) with s

′′

> s, such

that the minimal level of (s

′′

h, k

′′

) is smaller than

s. After less than 2

sh+1

hash computations minimal

level of (s

′′

h, k

′′

) will be at least sh. Besides that,

there are also jobs with lower indices that must be

completed before (sh, k ) can be completed. There are

at most 2

(s−s

′

such jobs for every s

′

< s. All jobs

on level s

′

h require less than 2

(s−s

′

h+1

= 2

computation units for every s

′

< s. Hence, the total

number of computation units needed for these jobs is

(s − 1)2

. Thus we have 2

sh+1

computation units

left to complete the job (sh, k).

Lemma 2 At every moment of time there is only one

running job on level sh, s = 1, 2, . . . , L.

Proof: At time 0 we start only one job on level sh.

For every level sh and every index i, we can prove

by induction using Lemma 1 that at time interval

i, 2

(i + 1)) there is only one running job with

index i on level sh.

Lemma 3 The computation of job (sh, i) will be ﬁn-

ished before time i2

Proof: Easily follows from Lemma 1 and Lemma 2.

In our computation only every h-th node on the

computation path is computed directly. Below we will

show which nodes should be retained during the com-

putation of (sh, i).

All nodes (ih − m, s2

+ j), where m = 1, . . . , h

and j = 0, . . . , m − 1 must be retained. In other

words, all descendants of (ih, s) at levels ih −

1, . . . , (i − 1)h must be retained.

Proposition 1 Descendants of a node (ih, m) are

needed during rounds [m2

, (m + 1)2

Proof: Indeed, children of (ih, m) are needed during

rounds [m2

h−1

, (m+1)2

) and [m2

, m2

h−1

). For descendants on other levels this proposi-

tion is proved by the fact that when a node is needed,

the sibling of its parent is also needed.

Combining Lemma 3 with Proposition 1, we see

that every node will be computed before it is needed

for the ﬁrst time.

4.2 Time Analysis

We have shown above that our algorithm performs 2L

hash function computations per round. Now we will

show that all other operations will take O(L) time per

round.

Lemma 4 Job scheduling, according to rules 1.-3.

can be implemented in O(L) time per round.

For every level s = ih we store a list Q

of level s

jobs that have to be performed. When a new job on

level ih becomes active or when the minimal level of

some job becomes smaller than ih, it is added to Q

Lists Q

are implemented as queues (FIFO).

At round j our algorithm checks all queues Q

ascending order. If a non-empty Q

is found, we

spend 2L hash computations on computing the last

job l in Q

. If the job l is ﬁnished after k < 2L hash

computations, or if the minimal level of l becomes

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

278

higher than (i + 1)h − 1 we remove l from Q

and

traverse queues Q

, Q

i+1

, . . . Q

until another non-

empty queue is found.

Procedure Eval can require up to H − 1 recursive

calls in the worst case. However, an equivalent non-

recursive implementation is possible (see procedure

EvalBottom in Appendix ).

5 THE LOWER BOUND

In this section we prove the lower bound on space and

time complexity of Merkle tree traversals and show

that the algorithm described above is asymptotically

optimal. We prove the following result:

Theorem 2 Any Merkle tree traversal algorithm

with average time per round O(log n/a) requires

Ω((log n/a)2

) space for any a > 1 .

In order to prove this theorem, we will consider only

time required for the hash computations.

First, we distinguish between nodes with even and

odd indices, further called even and odd nodes re-

spectively. Even internal nodes are needed after their

children. In case of odd internal nodes the situation

is opposite: they are needed before their children.

Namely, (s, 2i + 1) is needed during the time inter-

val [2i2

, (2i + 1)2

) and its children, (s − 1, 4i + 3)

and (s − 1, 4i + 2), are needed during [2

s−1

(4i +

2), 2

s−1

(4i+3)) and [2

s−1

(4i+3), 2

s−1

(4i+4)) re-

spectively. We can generalize this observation: an odd

node is needed before all its proper descendants. We

have just proved it for children; to extend the proof

by one more generation, observe that when a node is

needed and it is not the root, then the sibling of its

parent is needed.

During the computation, when we execute

v = Eval(s, i) = φ

(Eval(s−1, 2i), Eval(s−1, 2i+1))

we can remove v

= Eval(s − 1, 2i) and v

Eval(s − 1, 2i + 1) or not. Suppose that we are not

removing value v

, j = 0, 1, even though we will not

keep v

until it is needed . Then we can normalize

our algorithm by removing v

and keeping v instead:

computing v is the only use for v

other than including

it in a certiﬁcate. Clearly, this normalization increases

neither memory nor time.

For every odd node in a Merkle tree we do three

things: (a) we account for a certain number of steps –

steps used to compute this node using other remem-

bered values, (b) we account for a certain number of

memory units (one memory unit allows to store one

value through one round) and (c) we account for a

certain number of job units; job units correspond to

the steps that would be executed if this value were

computed from scratch.

Computing Eval(s, i) takes 2

s+1

− 1 computation

units, and in our lower bound reasoning we can esti-

mate this as 2

steps. By adding s’s over all needed

odd nodes we obtain the total number of job units.

The number of job units for odd nodes on level s

is 2

H−s−1

= 2

H−1

= n/2. Therefore the to-

tal number of job units for odd nodes of the Merkle

tree is Hn/2. We do not count the costs of comput-

ing needed values of even nodes in our lower bound

proof.

We account for the remembered values in order in

which children precede the parents.

Suppose that we remember the value of node v

during the computation of node v, but do not remem-

ber the value of v

, where v

is an ascendant of v

Then we can save more job units by remembering v

instead of v

. Hence, if we remember the value of v

on level l

during computation of node v on level l,

then values of all nodes on levels l

, l

+ 1, . . . , l are

also remembered. Therefore when a node on level s

is computed it is either computed “from scratch” with

s+1

− 1 steps or it is computed with 1 step because

its children were already computed and remembered.

Suppose that we remember the result Eval(s, 2i +

1) and we use this value a times for computation of

node values (including node (s, 2i+1) ). The last use,

when Eval(s, 2i + 1) is needed, requires 2

memory

units. If we want to use this value twice, we have to

compute it before its parent (or other odd ancestor is

needed), and since the parent (ancestor) is needed for

s+1

rounds or more, we need at least 2

s+1

memory

units. By induction, if we want to use Eval(s, 2i +

1) for a node values, we need to use at least 2

a−1

memory units.

Consider a node (s, 2i + 1). Suppose that its value

was used in a computations. As shown above, we

need either 2

s+1

− 1 steps or 1 step to compute it. If

we need 1 step, then the total number of job values

we accounted for is a, and the total number of mem-

ory units is 2

a−1

. Suppose that we needed 2

s+1

−1

steps to compute (s, 2i + 1). Then the total number

of job units is a(2

s+1

− 1), and the number of mem-

ory units is 2

a−1

. Now we can distribute the steps

and memory units between the job units that we have

accounted for. Each of them receives a

−1

steps and at

least 2

a−1

/a memory units.

If we use z

to express the amount of steps a

job unit k = 1, 2, . . . , Hn/2 obtains, then the min-

imal number of obtained memory units is f(z

) =

1/z

. Note that f (z) is a convex function of z

(the second derivative is positive for positive z). The

total number of steps

= Hn/2a. Since f(z) is

convex,

Hn/2

f(z

) ≥ f(

Hn/2

) and

f(z

) ≥

(Hn/2)f(a) = 2

/a × Hn/4

Thus we have shown that if the computation takes

Hn/2a steps, then it uses at least 2

/a×Hn/4 mem-

OPTIMAL TRADE-OFF FOR MERKLE TREE TRAVERSAL

279

ory units. Since the total number of rounds is n,

during an average round we must remember at least

/4a values.

6 A CONSTANT IMPROVEMENT

In this section we describe an improved version of

the algorithm from the section 4. In our improved

version we do not compute all nodes in the subtrees.

Instead of this, only the nodes with odd indices are

computed. This is possible because even nodes will

be needed after their children are needed. Therefore,

if we store both children of an even node until their

parent is needed, we can compute its value with one

hash computation.

Thus, in a subtree (ih, k) we only compute nodes

(ih − 1, 2k + 1), (ih − 2, 4k + 1), (ih − 3, 8k + 1), . . .

and only the nodes (ih − 1, 2k + 1), (ih − 2, 4k +

1), (ih − 2, 4k + 3), . . . , (ih − h, k2

+ 1), . . . , (ih −

h, k2

+ 2

− 1) must be stored. (see an example on

Fig. 3)

Computation of all odd descendants of (ih, k) will

take time 2

ih−1+1

−1+2

ih−2+1

−1+. . .+2

ih−h+1

−

1 =

h−1

k=0

ih−k

− h = 2

ih+1

− 2

(i−1)h+1

− h. We

will need h extra hash computations to compute the

even nodes. Therefore the total number of computa-

tions for subtree (ih, k) is 2

ih+1

− 2

(i−1)h+1

It is easy to see that there is at most one “new” even

node at every round. Therefore it takes at most one

extra computation per round to deal with even nodes

(if we compute even nodes just as they are needed ).

To compute the node (s, j) with one hash computa-

tion we have to store its odd child (s−1, 2j+1) during

rounds [(2j + 1)2

s−1

, (2j + 2)2

s−1

). Thus there are

at most h odd nodes that should be kept “extra time”

and at most h nodes that are a part of an authentica-

tion path during each round. Therefore the total mem-

ory requirement is (2

− 1 + 2h)L per subtree. We

need the ﬁrst summand to store the odd nodes in the

subtree and we need the second summand to store the

even nodes from the current authentication path and

odd nodes kept “extra time”.

The nature of our trade-off depends on the subtree

height h. For subtree height h = 1 this improvement

results in speed-up of almost factor 2. This allows us

to formulate the following result

Corollary 2 A Merkle tree traversal algorithm can

be implemented with log n hash function evalua-

tions, 3 log n memory locations for hash values and

O(log n) time for other operations per round

For larger values of h the time improvement be-

comes very small but we have an almost two-fold de-

crease of the space used by hash values. In the last

case we can also schedule our computation in such

way that the values in the next subtree are computed

almost exactly at the time when the corresponding

values in the current subtree “expire” and can be dis-

carded. In this case at most one extra value per sub-

tree would have to be stored. In our modiﬁed pro-

cedure computation of odd nodes of subtree (ih, k),

i = 2, 3, , . . . , L − 1 is divided into two stages. In

the ﬁrst stage descendants of (ih, k) on level (i − 1)h

(“leaves” of the subtree) are computed. We will fur-

ther call nodes ((i − 1)h, 2

k + j), j ∈ [0, 2

) bot-

tom level nodes of subtree (ih, k). In the second stage

the odd nodes are computed from bottom level nodes.

Observe that computation of the subtree (ih, k) takes

place in the same time interval [2

(k − 1), 2

k) as

in our ﬁrst algorithm. The idea of our modiﬁcation is

that nodes ((i − 1)h, 2

k + j), j ∈ [0, 2

), i.e. bot-

tom level nodes of (ih, k), are computed slower than

odd nodes of subtree (ih, k − 1) are discarded. Com-

putation of the odd nodes from the bottom tree nodes

is performed during the last 2

rounds of the inter-

val [2

(k − 1), 2

k). We will further call the jobs

computing the bottom level nodes secondary jobs,

and the last job computing the remaining odd nodes

of the subtree will be called a primary job. In order

to reserve 2

rounds for the primary job, we allocate

(i−1)h

−1 rounds for computation of every secondary

job. A pseudocode description of the modiﬁed proce-

dure Eval is given in Appendix.

Now we prove the space bound of our modiﬁed al-

gorithm. First we show that a secondary job of a node

on ih can be completed in 2

(i−1)h

− 1 rounds.

Lemma 5 Suppose that at time (k − 1)2

(i−1)h

− m, m = 0, 1, . . . , 2

− 1 for every level

l = h, 2h, . . . , (i − 1)h, (i + 1)h, . . . Lh there is at

most one unﬁnished secondary job of a job on level l.

Then the m-th secondary job of (ih, k) will complete

before (k − 1)2

+ (m + 1)2

(i−1)h

− m − 1 .

Proof: Consider the time interval [(k − 1)2

(i−1)h

−m, (k −1)2

+(m+1)2

(i−1)h

−m−1).

There is at most one job (i

′′

h, k

′′

) with i

′′

> i,

such that the minimal level of (i

′′

h, k

′′

) is smaller

than i. After at most 2

ih+1

− 2 hash computations

minimal level of (i

′′

h, k

′′

) will be at least ih. Be-

sides that, there are also jobs on lower levels that must

complete before (sh, k) can be completed. There are

at most 2

(i−i

′

such jobs for every index 1 < i

′

< i.

Thus for any ﬁxed i

′

< i all jobs on level i

′

require

(i−i

′

h+1

− 1) < 2

ih+1

− 2 job units. Another

h+1

− 1)2

(i−1)h

< 2

ih+1

− 2 computation units are

claimed by subtrees on level h. Hence the total num-

ber of computation units required by all other jobs is

strictly less than (L − 1)(2

ih+1

− 2).

Thus we have at least 2

ih+1

− 1 computation units

left to complete the m-th secondary job of (ih, k).

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

280

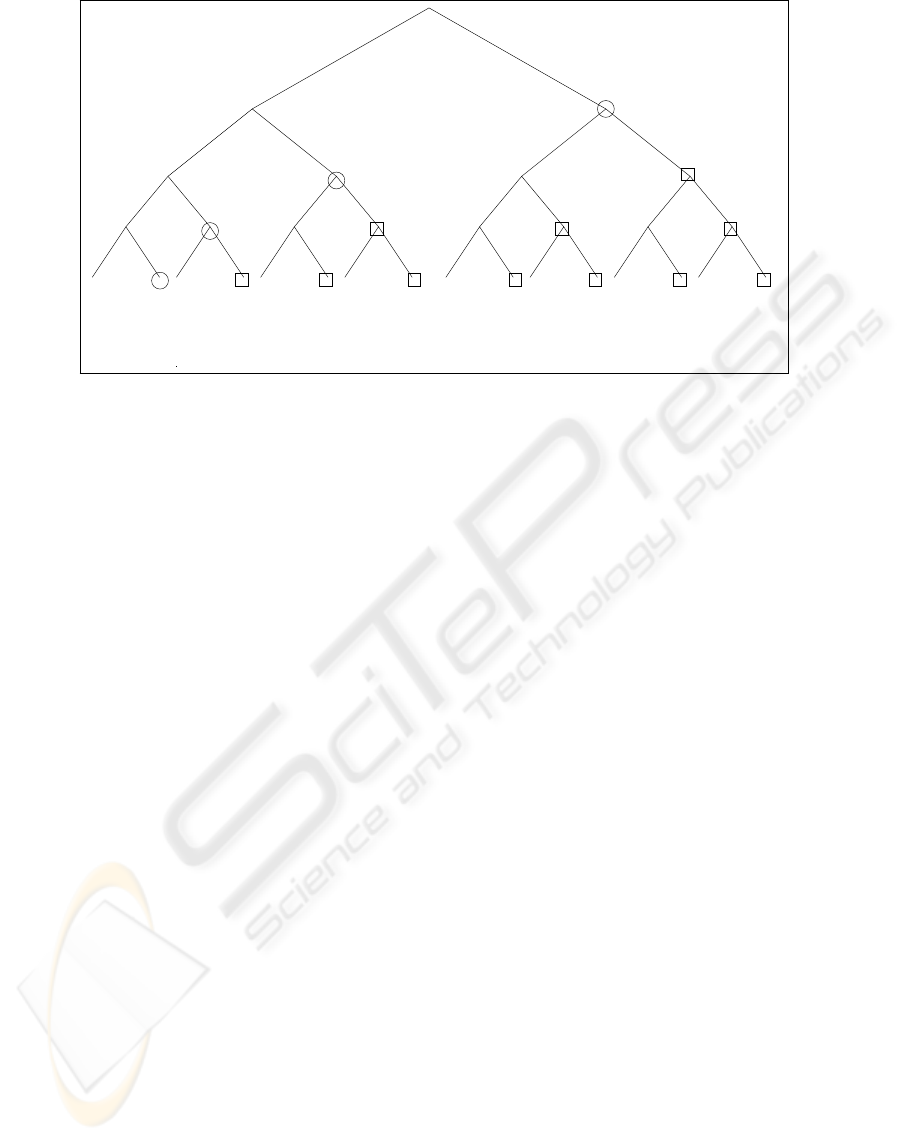
Figure 3: Example of a subtree. Computed nodes are marked by circles. Nodes marked by circles or squares are stored.

Lemma 6 Computation of the m-th secondary job of

(ih, k), i = 2, 3, . . . , L−1 will be ﬁnished before time

(k − 1)2

+ (m + 1)2

(i−1)h

− m − 1

Proof is analogous to the Proof of Lemma 3

It easily follows from Lemma 6 and the above dis-

cussion that the computation of the m-th bottom node

of (sh, k) will be ﬁnished in interval [2

(k − 1) +

(i−1)h

−m, 2

(k−1) +(m+1)2

(i−1)h

−m−1). It

remains to compute how many odd nodes of (ih, k −

1) are discarded before 2

(k − 1) + m2

(i−1)h

− m.

Let w = 2

. After 2

h(i−1)

m rounds the number

of remaining nodes can be estimated as (w − m)/2 +

(w−m)/4+. . .+(w−m)/w ≤ (w−m). We did not

count the nodes of the current authentication path in

this estimation. Therefore the total number of stored

nodes in subtrees (ih, k) and (ih, k − 1) in interval

(k − 1), 2

k − 2

) is limited by 2

The primary job for (sh, k) can be computed in 2

rounds. This job can be performed in-place, because

when a new node is computed its even child can be

discarded.

In the modiﬁed algorithm we apply the job schedul-

ing scheme only to subtrees on levels ih, i =

2, . . . , L−1. Since there is only one subtree for i = L,

it is not recomputed. Therefore the total number of

tail nodes does not exceed H − h.

During each round we use two reserved computa-

tion units to compute the next level h subtree. By

the same argument as above we can see that the num-

ber of remaining nodes in the current level h subtree

after m rounds is limited by 2

− m . Therefore

the total number of nodes in the current and future

subtrees of level h is limited by 2

. This computa-

tion would require up to h additional units for the tail

values. Therefore the total number of tail values is

H − h + h = H.

The above considerations allow us to formulate the

following

Theorem 3 A Merkle tree traversal can be imple-

mented in O(L) time with 2L hash operations. This

algorithm requires L2

+ 2H memory locations to

store hash values.

In the last Theorem we have ignored time neces-

sary to output the log n values per round. The re-

sult described in the abstract follows if we choose

h = log

(3)

7 CONCLUSION

In this paper we describe the ﬁrst optimal trade-off be-

tween time and space complexity of Merkle tree tra-

versals.

We believe it is possible to improve further the con-

stants in the described trade-off by differentiating be-

tween various types of nodes in our procedure.

Another interesting problem was described in

(Szydlo, 04): given space to store only S hash nodes,

what is the minimal number of hash computations per

round? (Szydlo, 04) proposes it in a combination with

(Jakobsson et al., 03) as a starting point of this inves-

tigation.

Yet another interesting problem is the complexity

of the traversal of the so-called skew (unbalanced)

Merkle trees (Karpinski, Nekrich, 04).

OPTIMAL TRADE-OFF FOR MERKLE TREE TRAVERSAL

281

REFERENCES

Coppersmith,D., Jakobsson,M., “Almost Optimal Hash Se-

quence Traversal”, Financial Cryptography, 2002,

102-119

Devanbu, P., Gertz, M., Martel,C., Stublebine, S. G., “Au-

thentic Third Party Data Publication” 14th IFIP Work-

shop on Database Security, 2000

Jakobsson, M., “Fractal Hash Sequence Representation and

Traversal”, ISIT, 2002, p. 437

Jakobsson, M., Leighton, T., Micali, S., and Szydlo, M.,

“Fractal Merkle Tree Representation and Traversal”,

RSA Cryptographers Track, RSA Security Confer-

ence, 2003.

Karpinski, M., Nekrich, Y., A Note on Traversing Skew

Merkle Trees, ECCC Report TR04-118.

Lipmaa, H “On Optimal Hash Tree Traversal for Optimal

Time Stamping”, Proc. Information Security Confer-

ence, 2002, LNCS 2433, 357-371.

Merkle, R., “Secrecy, Authentication and Public Key Sys-

tems”, UMI Research Press, 1982

Merkle, R., “A Digital Signature Based on a Conventional

Encryption Function”, Proc. Crypto 1987, 369-378.

Micali, S., “Efﬁcient Certiﬁcate Revocation” , Technical

Report TM-542b, MIT Laboratory for Computer Sci-

ence, March 22, 1996

Micali, S., Rabin, M., Kilian, J., “Zero-Knowledge Sets”,

Proc. 44th FOCS, 2003, 80-91 .

Perrig, A., Canetti, R., Tygar, D., Song D., “ The TESLA

Broadcast Authentication Protocol” , Cryptobytes, vol

5, pp. 2-13. Available at

http://citeseer.nj.nec.com/

perrig02tesla.html

Rivest, R., Shamir, A., “PayWord and MicroMint - Two

Simple Micropayment Schemes”, CryptoBytes, vol.

1, pp. 7-11. Available at

theory.lcs.mit.edu/

∼rivest/RivestShamir-mpay.ps

Szydlo, M., “Merkle Tree Traversal in Log Space and

Time”, Proc. Eurocrypt 2004, LNCS 3027, 541-554.

APPENDIX

In this Appendix we give a pseudocode description

of the modiﬁed procedure Eval(A,k), A = ih. Recall

that ﬁrst all descendants of (A, k) on level (i−1)h are

computed and computation of the m-th descendant

starts at time 2

(k − 1) + 2

(i−1)h

m − m. Procedure

EvalBottom is algorithmically identical to procedure

Eval in section 3. That is, the same sequence of hash

computations is performed. Therefore all proofs in

section 4 remain valid if we use EvalBottom or Eval1

Eval1 (A,k)

i := A/h

if ( round = 2

(k − 1) + 2

(i−1)h

m − m)

bottom[m] := \

EvalBottom(2

(i−1)h

, m+(k−1)2

)

EvalTop(A, k)

Figure 4: Procedure Eval1

instead of Eval . However the implementation pre-

sented here does not use recursion. Observe that vari-

ables T ail

lev

are global, i.e. common for all proce-

dures EvalBottom.

EvalBottom (A,k)

ind := 2

minlev := lev := 0

while (lev < A)

V := φ

(ind)

while (ind mod 2 = 1)

V := φ

(T ail

lev

, V )

lev := lev + 1

minlev := minlev + 1

ind := ind/2

T ail

lev

:= V

ind := (ind + 1)2

lev

minlev := lev := 0

EvalTop (A,k)

ind := 2

minlev := lev := 0

while (lev < A)

V := bottom[ind]

while (ind mod 2 = 1)

lef tind := 2

lev

ind

rightind := 2

lev

(ind + 1)

bottom[lef tind] := \

(bottom[lef tind], bottom[rig h tind])

lev := lev + 1

minlev := minlev + 1

ind := ind/2

ind := (ind + 1)2

lev

minlev := lev := 0

Figure 5: Procedures EvalBottom and EvalTop

Procedure EvalTop(A,k) computes all odd nodes of

the height h subtree rooted in (A, k) if all descendants

of (A, k) on level (i−1)h are known. The pseudocode

is very similar to EvalBottom but EvalTop(A,k) works

in-place, i.e. with only a constant number of addi-

tional variables.

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

282