
GUARANTEERRING SECURITY OF FINANCIAL TRANSACTION
BY USING QUANTUM CRYPTOGRAPHY IN BANKING
ENVIRONMENT
Solange Ghernaouti-H
´
elie and Mohamed Ali Sfaxi
HEC - University of Lausanne
1015 Switzerland
Keywords:
Security guarantee, Quantum cryptography, Key management, secure financial transactions, IPSEC, perfor-
mances.
Abstract:
Protocols and applications could profit of quantum cryptography to secure communications. The applications
of quantum cryptography are linked to telecommunication services that require very high level of security
such as bank transactions.
The aim of this paper is to present the possibility to use quantum cryptography in critical financial transactions,
to analyse the use of quantum key distribution within IPSEC to secure these transactions and to present the
estimated performances of this solution.
After having introduced basic concepts in quantum cryptography, we describe a scenario of using quantum
key distribution in bank transactions in Switzerland. Then, we propose a solution that integrate quantum
key distribution into IPSEC. A performance analysis is done to demonstrate the operational feasibility of this
solution.
1 INTRODUCTION
Banks and financial establishments need to secure
transaction and communication between them and
their clients. In fact, everyday thousand of million
dollars transactions are performed between banks.
This transmission must be secure and need to satisfy
security requirement such as authentication, confiden-
tiality and integrity. Quantum cryptography could be
used, in this context, to offer unconditional secure
communication.
The next section presents a scenario for quantum
cryptography application to secure bank transaction
over Internet and Intranet architectures. Then, we
prove the feasibility of the use of quantum cryptog-
raphy within the framework of IPsec.
Quantum cryptography could be applied to IP Se-
curity protocol (IPsec) [RFC 2401]. This protocol is
related to a collection of standards that was designed
specifically to create secure end-to-end secure con-
nections. The standard was developed by the Internet
Engineering Task Force (IETF) to secure communi-
cations over both public and private networks.
2 QUANTUM CRYPTOGRAPHY
FOR BANKS AND FINANCIAL
ESTABLISHMENTS
Nowadays, Banks and financial institutions use either
symmetric cryptography or asymmetric cryptography.
Both techniques, as proved above, are not uncondi-
tionally secure. So transactions could be corrupted
and altered without the awareness of the bank. This
constitutes a serious danger because criminals and
malicious organizations could profit of the breach to
steal and highjack. Securing critical financial transac-
tion is mandatory and will be more and more neces-
sary to master economical crime.
2.1 Quantum Cryptography solution
To ensure maximum security, we need to maximize
the security in each field such as storage, generation,
processing and transmission of data. In this para-
graph, we will focus on securing transmissions. The
transmissions are either from bank building to another
bank building of the same company, from cash dis-
penser to bank and from a bank to another. The dif-
ference resides in the distance, the degree of security
268
Ghernaouti-Hélie S. and Ali Sfaxi M. (2005).
GUARANTEERRING SECURITY OF FINANCIAL TRANSACTION BY USING QUANTUM CRYPTOGRAPHY IN BANKING ENVIRONMENT.
In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 268-274
DOI: 10.5220/0001414102680274
Copyright
c
SciTePress

required and the duration and the quantity of infor-
mation to send. Quantum cryptography ensures the
unconditional security of transmission and the aware-
ness if an eavesdropper tries to intercept or modify
the content of the transmission. Quantum cryptog-
raphy aims exploiting the laws of quantum physics
in order to carry out a cryptographic task. The un-
certainty relations of Heisenberg can in particular be
exploited to implement communication channels that
cannot be passively - i.e. without disturbance of the
transmission - eavesdropped. Its legitimate users can
detect eavesdropping, no matter what technology is
available to the spy (Bennet1984; Gisin2002).
The power of quantum cryptography lies primarily
in the fact that the keys distributed on the quantum
channel are invulnerable to eavesdropping and can
be guaranteed without assumptions on the comput-
ing power of an eavesdropper (Mayers1998; Lo1999).
Banks can actually use quantum cryptography at least
in two of the three types of transaction: bank build-
ing to another bank building of the same bank com-
pany or/and cash dispenser to the bank. In fact, we as-
sume that the distance connecting two bank buildings
in less than 100 km. So, the use of quantum cryptog-
raphy based on optical fiber is possible (IdQuan2004).
In this case, either a big amount of data could be ex-
change or a tiny amount of data that could be transmit-
ted frequently between bank buildings. Transmission
from cash dispenser to banks (if the cash dispenser is
not in the bank) can also be done using quantum cryp-
tography based on optical fiber. In fact, the danger is
that a malicious person could intercept the communi-
cations between the bank and the cash dispenser and
modify them like for instance credit some bank ac-
count or change the identification of debited account.
Transaction, using quantum cryptography, would be
at that moment unconditionally secure and no one can
intercept them. Here we ensure the integrity and the
confidentiality of the transmitted data.
Figure 1: Swiss bank - application of quantum cryptogra-
phy
2.2 Example of a bank scenario
In this paragraph, we present a scenario of quantum
cryptography implementation in Switzerland (small
country size). The bank company is called Swiss
Bank (SB). We assume that each bank have a head
quarter in every Canton. A main data base is located
in Zurich and every head quarter bank has to commu-
nicate all transaction to the data base in Zurich. SB
installs optic fiber between some head quarters in or-
der to create a ”private” quantum network (Figure 1).
At least, each head quarter has a quantum cryptogra-
phy receiver/sender. In order to reduce the volume of
exchanged data every 6 hours all head quarters send
data about transaction to Zurich (6h30, 12h30, 18h30
and 0h30).
The steps are the following:
All head quarters gather all transactions realized in
the Canton. Bank head quarter located in the far-
thest Cantons from Zurich sends their adjacent can-
ton. For instance, Lugano’s SB head quarter sends
data to Bellinzona, Poschiavo sends to Brigue... us-
ing quantum cryptography. These ”nodes” has to wait
until all adjacent cantons send have finished sending
data (or time-out) then decrypt data and send them
to the following BS head quarter according to a list.
Finally, the nearest and direct linked to Zurich head
quarters (Winterthur, Zoug, St-Gall, Coire...) ex-
change keys and communicate in a secure way using
quantum cryptography.
Every head quarter (say H) has two different lists.
Reception list: it is a list of all the head quarters that
send data to H. Send List: usually it contains only one
head quarter (the nearest to Zurich) but for availability
purpose it contains 2 BS head quarters.
Example of such lists (for Bellinzona):
Reception list Send list
Lugano Coire
St-Moriz
Ascona
The possible cost of such scenario is:
The optical fiber total length: about 2000 Km
Number of quantum cryptography station: (twice the
number of links) about 80
The cost of optical fiber per meter = 6 CHF
The cost of 2 quantum cryptography station = 150,000
CHF
The total cost of the scenario is 12000000 + 6000000
= 18 Million CHF 12 Million Euros.
So the price to ensure an unconditional secure trans-
mission is about 12 Million Euros.
This cost is huge but if we estimate the prestige gain
(in the image, the reputation and in term of confi-
dence) of the bank this expense is justifiable. This
long term investment will be beneficial to the bank.
GUARANTEERRING SECURITY OF FINANCIAL TRANSACTION BY USING QUNATUM CRYPTOGRAPHY IN
BANKING ENVIRONMENT
269
To apply this solution, we need to use algorithms
and protocols. IPsec could support the use of quan-
tum cryptography. We present the feasibility and the
theoretical performances of such application.
3 SEQKEIP OPERATING MODE
As IPsec uses classical cryptography to secure com-
munication, in this paragraph, we propose to use
quantum cryptography to replace the classical cryp-
tographic protocols used for symmetric distribution.
Using QKD in IPsec has already been proposed
and implemented by Elliot of BBN technologies (El-
liott2002). It proposes the idea of using QKD in IPsec
as Key generator for AES. In 2003, BBN technologies
describes the possibility of integrating QKD within
the standard IKE (Elliott2003) and announces some
concerns linked to the compatibility of QKD with
IKE. In our paper, we propose a QKD solution for
IPsec called SEQKEIP that is not based on IKE but
on ISAKMP. Using this method, we avoid the prob-
lem of compatibility between IKE and QKD.
The idea is to stick to the traditional IPsec and the
Internet Security Association and Key management
Protocol (ISAKMP). In fact, ISAKMP does not im-
pose any condition to is the negotiation mechanisms
or to the SAs parameters. To use quantum cryptog-
raphy with IPsec we have simply to define the two
phases described above. We create a Secure Quan-
tum Key Exchange Internet Protocol (SeQKEIP). The
SeQKEIP like IKE uses ISAKMP mechanisms and
takes advantage of quantum cryptography in order to
build a practical protocol.
SeQKEIP runs nearly like the IKE. It includes
3 phases: the phase 1 for the negotiation of the
ISAKMP SA, phase 2 for the negotiation of SA and
we add a phase called ”phase 0” in which Alice
and Bob will share the first secret key. There are
only three modes in SeQKEIP: Quantum Mode, Main
Mode and Quick mode. Quantum mode is the quan-
tum cryptography key exchange in the phase 0. Main
Mode is used during the phase 1 and Quick Mode is
an exchange in phase 2. Both the Main Mode and the
Quick Mode are nearly the same of those in IKE.
Phase 0: Key exchange - Quantum Mode
This phase is the beginning of the secure exchange
using quantum cryptography. After, these exchange
both the sender and the receiver share a secret key.
This key constitutes the pre-shared secret in IKE
mechanism.
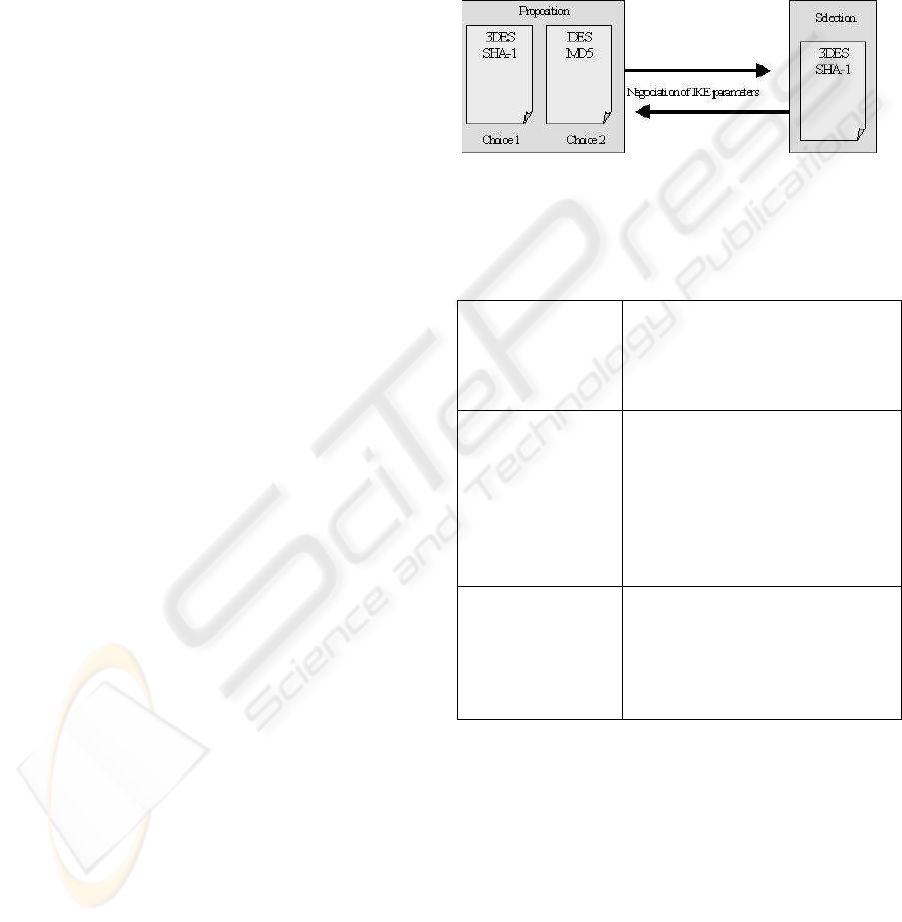
Phase 1: Negotiation of ISAKMP SA - Main Mode
During this phase, the cryptographic algorithm and
the hash function are negotiated. Only the two pa-
rameters discussed in the phase 1 constitute the Se-
QKEIP attribute. The method to authenticate is
the pre-shared secret (the secret key exchanged with
Quantum Key Exchange method). Contrarily to IKE,
SeQKEIP do not define DH groups and do not need
to use digital signature nor digital certificates (Figure
2). No cryptographic key are generated in this phase.
The first exchanged key is used to encipher packets
and to authenticate users.
Figure 2: Message exchanged during the first phase
After the phase 0 and the phase 1, both sender and
receiver will have the following information:
Shared secret key This key is generated during the
phase 0 with Quantum Key ex-
change mechanism. The secret
key is used to authenticate users
and to encrypt packet.
Encryption algo-
rithm
The encryption algorithm is ap-
plied to the phase 2 (negotia-
tion of SA parameters). The al-
gorithm could be 3DES, DES,
AES. But, if we want to have
the maximum security, we have
to use One-Time-Pad function
(OTP).
Hash function The hash function will give the
opportunity to the sender and
the receiver to check the in-
tegrity of the message and the
authentication of the correspon-
dents.
Note that the phase 0 and the phase 1 are totally
independent and could be done at the same time. We
need the secret key only from the phase 2.
Phase 2: Negotiation of SA - Quick Mode
As in IKE, the exchanged messages in phase 2 are
protected in authentication and confidentiality by the
negotiated parameters of the phase 1 and phase 0. The
authentication is guaranteed by the addition of the
HASH block after the ISAKMP header and the con-
fidentiality is ensured by the encryption of the whole
message blocks. The aim of this phase is to nego-
tiate the SA. i.e. to negotiate the ”IPsec” parame-
ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS
270
ters. The SA parameters are (Mason2002): Desti-
nation address, Security Parameter Index (SPI), the
security mechanism (AH or ESP) and encryption &
Hash function, the session key and additional attribute
like the lifetime of SA.
For SeQKEIP, to extend security, we can use One-
Time-Pad encryption function. The first exchanged
key, in this case, will have the length of the message.
We do not need thus any encryption algorithm for SA.
We still need a Hash function to verify the integrity of
the data. The run of IPsec could be modified in order
to use one-time-pad function.
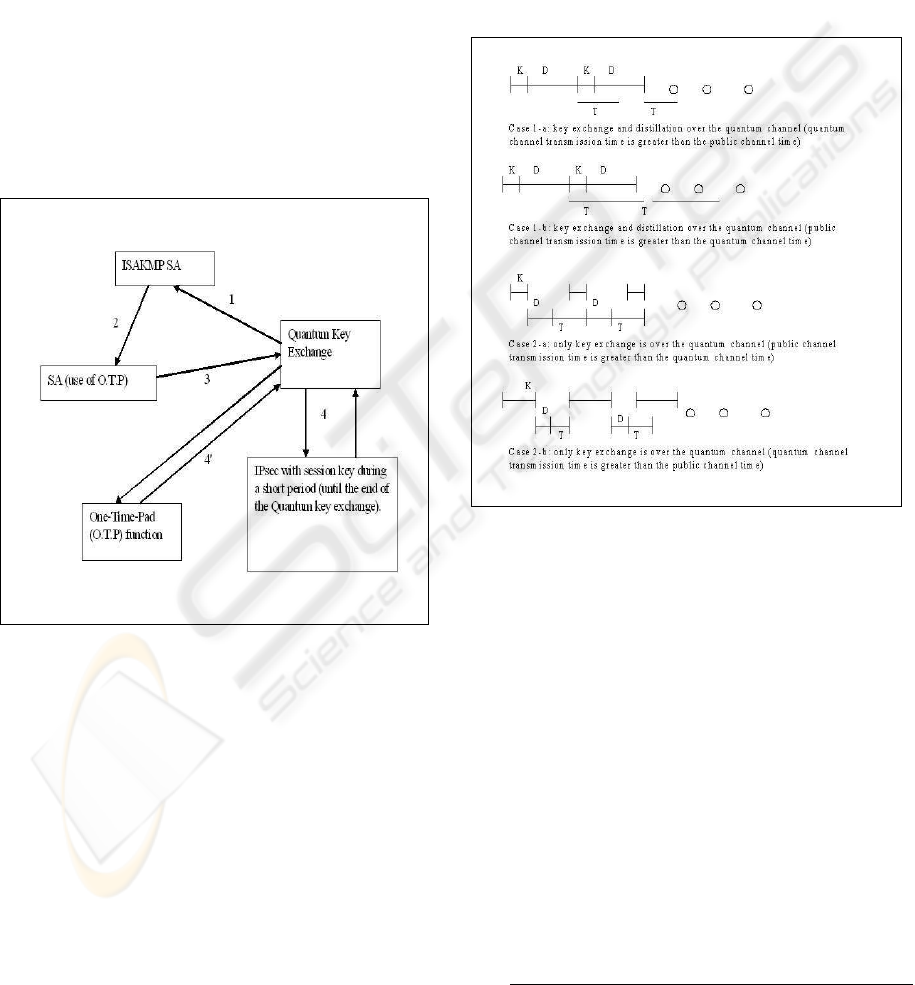
In the beginning (Figure 3), the phase 0 and the
phase 1 start (1&2). After these two phases the para-
meters of the protocol are fixed. In (3), we will use
key exchanged thanks to quantum cryptography. This
key will be used either as a session key (4) or in the
one-time-pad function (4’).
Figure 3: Functioning of IPsec with Quantum Cryptography
In (4), we use traditional symmetric cryptography
algorithms to exchange data. The IPsec packets are
the same as without the use of quantum cryptography.
The session key, therefore, is exchanged using quan-
tum key exchange. The lifetime duration of the ses-
sion key is very short and it is equal to the time needed
to exchange the secret key using quantum cryptogra-
phy. This solution is a transition solution to the (4’)
In (4’), we use quantum cryptography concepts to-
tally. The idea is to shift completely to the uncon-
ditional secure functions .i.e. quantum key exchange
and one-time-pad function. After fixing the SA para-
meters, the ”session” keys length will be of the size
the data in the IPsec packet. Then, it is possible to use
one-time-pad function (simply perform an XOR of
the message and the key and then send the result). We
need to exchange key for every packet. The weakness
of this solution resides in the time needed to exchange
the key. The total bit rate is highly affected due to this
problem but as the quantum cryptography technology
is progressing, this issue will soon be solved.
There are two possibilities. The first case is to
exchange the key and distillation using the quantum
channel (Time division multiplexing). The other is to
exchange only the key over the quantum channel and
all the other data over the public channel (Figure 4).
Figure 4: the two cases of using totally quantum cryptogra-
phy in IPsec
K: the duration to exchange the quantum key
D: the duration of key distillation
T: the duration of transmitting the message
1-first solution:
In this case, we propose to use the quantum channel
to exchange the key and for distillation. There are two
possibilities: K+D is greater than T (K+D>T) and
K+D is less or equal to T (K+D≤T).
The effectiveness (θ) of this solution is given by ( θ
represents the difference between the use of quantum
cryptography and the use of unenciphered transmis-
sion):
a- K+D > T
If K+D>T then
θ =
T × N
(K + D) + T × N + (N − 1) × ((K + D) − T )
(1)
GUARANTEERRING SECURITY OF FINANCIAL TRANSACTION BY USING QUNATUM CRYPTOGRAPHY IN
BANKING ENVIRONMENT
271

Where N is the number of packet.
θ =
T × N
(K + D) + T × N − (N − 1) × T + (K + D) × (N − 1)
(2)
Finally, after simplification:
θ =
T × N
T + (K + D) × N
(3)
If N is very large (infinite), θ is equal to:
lim
N →∞
θ =
T
K + D
(4)
Example 1 Traditionally, the size of MTU (Maximum
Transmission Unit) is 1500 bytes (i.e. 12 Kbits); we
suppose that the unprotected header size is 250 bytes,
so we have to secure 1250 bytes i.e. 10 Kbits. There-
fore, the key length will be 10Kbits if we want to use
One-Time-Pad function. The flow rate to exchange
the key is 1 MBit/s and about 100 MBit/s to exchange
normal data on optical fiber. We suppose that we
have an Internet connection of 1 Mbit/s. As the error
rate for exchanging quantum key is normally 50%, we
need to exchange 20 Kbits in order to get 10Kbits of
key length. We estimate the distillation data to be 40
Kbits. The time to XOR data with the key is neglected.
Having the previous assumption:
K = 20/1000 = 0.02 s
D = 40/100000 = 0.0004 s
And T = 12/1000 = 0.012 s
In this case, K+D (20.4 ms) is greater than T (12
ms). The effectiveness θ when the number of packet
N is infinite (4) is equal to 120/204 ˜60 % of the total
performance.
NB: if we have a faster Internet connection, say
10Mbit/s, the effectiveness θ given by (4) will be
equal to 6 % of the total performance. In this case,
the use of SeQKEIP is useless if we see only the per-
formance. But, as the rate of quantum key exchange
is progressing the effectiveness will increase.
b- K+D≤T
If K+D≤T then
θ =
T × N
(K + D) + T × N
(5)
if N is very large (infinite), θ is equal to:
lim
N →∞
θ =
T
T
= 1 (6)
So, in this case, there is no difference in the per-
formance between using SeQKEIP and IP. The addi-
tional time cost induced by the use of quantum cryp-
tography is negligible.
2-second solution
The quantum channel is used only to exchange the
key. The distillation is done over the public channel.
There are also two possibilities depending on the time
needed to exchange the key and, on the other hand, the
time to validate and send the message.
We take the same notation as previous:
K: the duration to exchange the quantum key
D: the duration of the key distillation
T: the duration of transmitting the message
So, we distinguish two scenarios: when K > D+T
and K ≤T+D.
a- K > D+T
If K>T+D then
θ =
T × N
K + (T + D) × N + (N − 1) × (K − (D + T ))
(7)
And, after simplification:
θ =
T × N
(T + D) + K × N
(8)
if N is very large (infinite), θ is equal to:
lim
N →∞
θ =
T
K
(9)
Example 2 We take the same parameters as in the
”NB” the previous example (10 Mbit/s for the Internet
connection, 1Mbit/s to exchange the quantum key).
Having the previous assumption:
K = 20/1000 = 0.02 s
D = 40/10000 = 0.004 s
And T = 12/10000 = 0.0012 s
In this case, K (20 ms) is greater than T +V (42 ms).
The effectiveness θ if the number of packet N is infinite
(9) is equal to 12/200 = 6 % of the total performance.
The flow rate configuration is the both solutions
gives the same performance rate (6 %) of the whole
performance. To upgrade this rate, the only solution
is to have the K ≤T+D in this case and K+D ≤T in
the previous solution.
b- If K≤T+D
If K≤T+D then
θ =
T × N
K + (T + D) × N
(10)
if N is very large (infinite), θ is equal to:
ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS
272

lim
N →∞
θ =
T
T + D
(11)
If we take the following configuration: the rate of
quantum key exchange is 1Mbit/s and the Internet
connection is 1Mbit/s, then T= 0.012 s and D = 0.04s.
T+V is greater than K (0.02 s). So, the effectiveness
θ if the number of packet N is infinite (11) is equal to
12/52 = 23 % of the total performance.
4 CONCLUSION
Classical cryptography algorithms are based on math-
ematical functions. The robustness of a given cryp-
tosystem is based essentially on the secrecy of its (pri-
vate) key and the difficulty with which the inverse of
its one-way function(s) can be calculated. Unfortu-
nately, there is no mathematical proof that will es-
tablish whether it is not possible to find the inverse
of a given one-way function. On the contrary, quan-
tum cryptography is a method for sharing secret keys,
whose security can be formally demonstrated.
As we have seen, using quantum cryptography in
conjonction with IPsec to offer a better level of se-
curity for organisations is possible. If, we apply the
quantum key exchange and one-time-pad function,
we reach the unconditional security in communica-
tion. The distillation of the quantum key could be
done in two different ways: over the optical chan-
nel or over the public channel. The cost of installing
this solution stills expensive nowadays. The perfor-
mance obtained when distilling the key over the op-
tical channel is higher than when using public chan-
nel (up to 100% when using optical channel versus
23% when using public channel). Actually, we can
reach 100Kbit/s when exchanging the quantum key
and hope to reach 1Mbit/s next few years. The possi-
ble flow rate over an optical fiber is 100Mb/s. If, we
use an Internet connection of 1Mbit/s, we get 60% of
the total performance (solution1, a) i.e. a flow rate
of 600Kbit/s if the distillation of the key is done over
the optical channel and we get only 23% of the to-
tal performance if we validate the key over the public
channel (solution 2, b) i.e. a flow rate of 230Kbit/s. If
we could reach the rate of 10Mbit/s in quantum key
exchange and we use the first solution, we will get a
performance of 100% in the flow rate i.e. 1Mbit/s.
ACKNOWLEDGEMENT
This work has been done within the framework
of the European research project : SECOQC -
www.secoqc.net. We would like to thank IDQuan-
tique S.A (www.idquantique.com) and specially Gre-
goire Ribordy and Olivier Gay for their help and use-
ful information.
REFERENCES
Ghernaouti-H
´
elie, S; Sfaxi, M.A; Hauser, A; Riguidel,
M;All
´
eaume, R (2004). “Business model: advan-
tages, scenarios, patents and laws related to quantum
cryptography”. Secoqc project deliverable.
All
´
eaume R (2004). “R
´
ealisation exp
´
erimentale de sources
de photons uniques, caract
´
erisation et application
`
a la
cryptographie quantique” (Secoqc partner)
Bennet, C; Brassard, G (1983). IEEE International Confer-
ence on Computers, Systems, and Signal Processing.
IEEE Press, LOS ALAMITOS
Bennet, (1992). C Quantum Cryptography: Uncertainty in
the Service of Privacy. Science 257.
Donald S.Bethune and William P.Risk (2002).
”AutoCompensating quantum cryptography”.
New journal of physics 4 (2002)42.1-42.15
URL: http://www.iop.org/EJ/article/1367-
2630/4/1/342/nj2142.html
Clark, C. W; Bienfang, J. C; Gross, A. J; Mink, A; Her-
shman, B. J; Nakassis, A; Tang, X; Lu, R; Su, D. H;
Williams, C. J; Hagley E. W; Wen, J (2000). ”Quan-
tum key distribution with 1.25 Gbps clock synchro-
nization”, Optics Express.
Artur Ekert (1991). “Quantum Cryptography based on
Bell’s Theorem”. Physical Review Letters. URL:
http://prola.aps.org/abstract/PRL/v67/i6/p661
1
Elliott, C (2002). ”Building the quantum network”. New
Journal of Physics 4 (46.1-46.12)
Elliott, C; Pearson, D; Troxel, G (2003). ”Quantum Cryp-
tography in Practice”.
Freebsd people. ”IPsec outline”. URL:
http://people.freebsd.org/˜julian/
IPsec
4 Dummies.html
freesoft (2004). ”IPsec Overview”. URL:
http://www.freesoft.org/CIE/Topics/141.htm
Gisin, N; Ribordy, G; Tittel, W; Zbinden, H. (2002).
”Quantum Cryptography”. Reviews of Modern
Physics 74 (2002): http://arxiv.org/PS
cache/quant-
ph/pdf/0101/0101098.pdf
Grosshans,Van Assche, Wenger,Brouri,Cerf,Grangier
(2003). ”Quantum key distribution using gaussian-
modulated coherent states” Letter to nature. URL:
http://www.mpq.mpg.de/Theorygroup/CIRAC-
/people/grosshans/papers/Nat421
238.pdf
R.Hughes,J.Nordholt,D.Derkacs,C.Peterson, (2002).
”Practical free-space quantum key distribu-
tion over 10km in daylight and at night”. New
journal of physics 4 (2002)43.1-43.14.URL:
http://www.iop.org/EJ/abstract/1367-2630/4/1/343/
Labouret, G (2000). ”IPsec: pr
´
esentation technique”. Herv
´
e
Schauer Consultants (HSC). URL : www.hsc.fr
GUARANTEERRING SECURITY OF FINANCIAL TRANSACTION BY USING QUNATUM CRYPTOGRAPHY IN
BANKING ENVIRONMENT
273

Lo, H.K; Chau, H.F. (1999). ”Unconditional se-
curity of quantum key distribution over
arbitrarily long distances”. Science 283:
http://arxiv.org/PS
cache/quant-ph/9803/9803006.pdf
Mason A, (2002). ”IPsec Overview Part Five:
Security Associations”. Cisco Press. URL:
http://www.ciscopress.com/articles/
printerfriendly.asp?p=25443
Mayers, D (1998). “Unconditionnal Security in Quantum
Cryptography”. J. Assoc. Comput. Math. 48, 351
Paterson, K.G; Piper, f; Schack, R (2004). ”Why Quantum
Cryptography?”. http://eprint.iacr.org/2004/156.pdf
Riguidel, M; Dang-Minh, D; Le-Quoc, C; Nguyen-Toan,
L; Nguyen-Thanh, M (2004). ”Quantum crypt- Work
Package I”. ENST/EEC/QC.04.06.WP1B. (Secoqc
partner)
Rivest, R.L; Shamir, A; Adleman, L.M (1978). ”A Method
of Obtaining Digital Signature and Public-Key Cryp-
tosystems”. Communication of the ACM 21 no. 2
1978.
Wootters, W.K; Zurek, W.H (1982). ”A single quantum can-
not be cloned”. Nature, 299, 802
IdQuantique (2004) ”A Quantum Leap for Cryptography”.
http://www.idquantique.com/files/introduction.pdf
ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS
274
