
On Swarm Optimality in Dynamic and Symmetric
Environments
⋆
Yaniv Altshuler
1
, Israel A. Wagner
1,2
and Alfred M. Bruckstein
1
1
Computer Science Department, Technion, Haifa 32000 Israel
2
IBM Haifa Labs, MATAM, Haifa 31905 Israel
Abstract. The field of multi agents and multi robotics has become increasingly
popular during the last two decades. The motivation behind multi agents based
systems is that many tasks can be much efficiently completed by using multiple
simple autonomous agents (robots, software agents, etc.) instead of a single so-
phisticated one. However, when examining such systems, one may be concerned
of the price-tag attached to the decentralized nature of swarm based approaches.
Meaning, while we simplify designs and control mechanisms in order to save
costs and computation resources, how far do our systems drift from optimal-
ity ? This work examines this issue by constructing an optimal algorithm for
the Dynamic Cooperative Cleaners problem (presented and analyzed in [2]). The
performance of the SWEEP algorithm of [2] is compared to this of an optimal
algorithm. The results of this comparison show that not only that the swarm al-
gorithm produces close results to the optimal solution, but also as the problem
gets harder, the performance of the two converge. In addition, insightful results
concerning optimal swarms in symmetric environments are presented.
1 Introduction
The fields of multi agents and multi robotics have become increasingly popular during
the last two decades. A multi agents system, or a swarm, can generally be defined as a
decentralized group of multiple autonomous units, either homogenous or heterogenous,
such that those units are simple and possess limited capabilities. Many research efforts
have been invested examining distributed systems models inspired by biology (behav-
ior based control model — [16,13], flocking and dispersing models — [22,18,19] and
predator-prey approach — [14,21]), physics [12], and economics [7–11]. The motiva-
tion behind multi agents and multi robotics systems is that by using multiple simple
autonomous agents instead of a single sophisticated one, many tasks can be performed
cheaply and easily, while the performance of those system remains satisfactory. In addi-
tion, such systems have several other advantages such as high scalability and adaptivity.
Application for which multi robotics systems fit successfully include covering, explo-
ration and patrolling [1], construction of complex structures and self-assembly [17, 15,
26], mapping and localizing [20, 27] and transportation [23,25, 24].
⋆
This research was partly supported by the Ministry of Science Infrastructural Grant No. 3-942
Altshuler Y., A. Wagner I. and M. Bruckstein A. (2005).
On Swarm Optimality in Dynamic and Symmetr ic Environments.
In Proceedings of the 1st International Workshop on Multi-Agent Robotic Systems, pages 64-71
DOI: 10.5220/0001196900640071
Copyright
c
SciTePress

However, when designing such systems, one must take into account the decrease in
performance which is inherent in such approaches, in comparison to an optimal central-
ized system (albeit much more complex and expensive).
In this work we examine this issue by constructing a centralized optimal algorithm
for the Dynamic Cooperative Cleaners problem (presented and analyzed in [2]. Similar
works appear in [4–6]). This problem assumes a grid, part of which is “dirty”, when the
“dirty” part is a connected region of the grid. On this dirty region several agents move,
each having the ability to “clean” the place it is located in. A deterministic evolution of
the environment is assumed, simulating a spreading contamination, or fire.
A cleaning algorithm designed to be used by a swarm of cleaning agents is pre-
sented and discussed in [2]. In addition, a lower bound over the cleaning time of agents
employing any algorithm (i.e. a lower bound over an optimal algorithm for the prob-
lem) is presented. The performance of the optimal algorithm described in section 4 is
compared to those of the sub-optimal SWEEP algorithm (described in section 3) and
the generic lower bound for the problem of [2].
The results of this comparison surprisingly show that although the SWEEP algo-
rithm is fully decentralized and extremely simple, assuming completely autonomous
agents and using no explicit form of communication, the improvements which can be
achieved by using an optimal algorithm is in no way significant enough to justify the
immense costs and complexity of such an algorithm.
In addition, several insightful and counter-intuitive results concerning optimal clean
strategies for symmetric environments are presented in section 6.
2 The Dynamic Cooperative Cleaners Problem
Let us assume that the time is discrete. Let G be a two dimensional grid, whose vertices
have a binary property of ‘contamination’. Let cont
t
(v) state the contamination state
of the vertex v in time t, taking either the value “on” or “off”. Let F
t
be the dirty sub-
graph of G at time t, i.e. F
t
= {v ∈ G | cont
t
(v) = on}. We assume that F
0
is a single
connected component. Let a group of k agents that can move across the grid G (moving
from a vertex to its neighbor in one time step) be placed in time t
0
on F
0
.
Each agent is equipped with a sensor capable of telling the condition of the square it
is currently located in, as well as the condition of the squares in the 8−Neighbors group
of the this square. An agent is also aware of other agents which are located in its square,
and all the agents agree on a common “north”. Each square can contain any number
of agents simultaneously. When an agent moves to a vertex v, it has the possibility
of causing cont(v) to become off. The agents do not have any prior knowledge of the
shape or size of the sub-graph F
0
except that it is a single connected component. Every
d time steps the contamination spreads. That is, if t = nd for some positive integer n,
then (∀v ∈ F
t
, ∀u ∈ 4−N eighbors(v) : cont
t+1
(u) = on). The agents’ goal is to
clean G by eliminating the contamination entirely, so that (∃t
success
: F
t
success
= ∅).
In addition, it is desired that this t
success
will be minimal.

3 The SWEEP Cleaning Algorithm
For solving the Dynamic Cooperative Cleaners problem the SWEEP algorithm was
suggested in [2]. The algorithm can be described as follows. Generalizing an idea from
computer graphics (which is presented in [3]), the connectivity of the contaminated re-
gion is preserved by preventing the agents from cleaning what is called critical points
— points which disconnect the graph of contaminated grid points. This ensures that the
agents stop only upon completing their mission. At each time step, each agent cleans
its current location (assuming this is not a critical point), and moves to its rightmost
neighbor — a local movement rule, creating the effect of a clockwise traversal of the
contaminated shape. As a result, the agents “peel” layers from the shape, while preserv-
ing its connectivity, until the shape is cleaned entirely.
4 An Optimal Cleaning Algorithm
In order to find the minimal cleaning time possible for a given contaminated shape F
0
,
we have designed a system in which all the cleaning agents are controlled by a central
unit (referred to as the queen). Upon initialization, the queen is given the complete
information regarding the contaminated shape. While the agents are traveling along the
grid, the queen is immediately aware of any new information discovered by the agents.
The queen’s orders as to the next desired movements of the agents are also immediately
transferred to the agents, which carry them out automatically.
Since the agents are completely bound to the desires of the queen, lacking even
the slightest amount of autonomy, this mechanism can be thought of as one big robot,
equipped with numerous long “cleaning hands”. Implementing such mechanism will
of course be very complicated and there is no doubt that such a robot will be very
expensive (remembering that the “cleaning hands” are capable of moving to very large
distances from one another). However, since we are interested in the optimality issue,
costs and complexity aspects are not of interest to us, at the moment.
For calculating the optimal solution to the problem, the queen uses the well known
A
∗
algorithm [28]. Upon initialization, the queen exhaustively searches for the shortest
path within the states space, where the initial state contains F
0
and the initial locations
of the agents. Every state can be developed into 2
k
states (since every agents can make
a single move clockwise or counterclockwise). Since the queen possesses complete
information regarding F
0
and knows exactly what the agents are doing, there is no
need for the agents to not clean certain contaminated squares (note that in the SWEEP
algorithm for example, sometimes the agents do not clean contaminated squares in order
to preserve the connectivity of the contaminated shape). Every d transitions between
states, the queen simulates a contamination spread. The success state is a state in which
there are no longer contaminated squares.
Once finding the shortest path within the states space from the initial state to a
success state, the queen starts moving the agents according to this path.
The optimality of this algorithm is immediately derived from the optimality of the
A
∗
algorithm in finding shortest paths in states spaces.

5 Experimental Results
A computer simulation of both the optimal algorithm described in section 4 and of
the SWEEP algorithm of [2] was constructed. Note that the size of the states spaces
covered by the optimal algorithm was at least :
2
k·f (F
0
)
(1)
where k is the number of agents, F
0
is the initial contaminated shape, and f() is the
lower bound over the cleaning time of [2], defined as :
f(F
0
) ≡ min{t|t ∈ N ∧ S
t
≤ 0} (2)
where :
S
t+d
≥ S
t
− d · k + (
p
8 · (S
t
− d · k) − 4 + 2) (3)
d is the number of time steps between contamination spreads and S
0
is the initial
area of F
0
, namely — S
0
= |F
0
|.
Three types of shapes were examined, varying in their convexity (i.e. their
S
0
c
0
value,
where c
0
is the initial circumference of the shape). Shapes whose
S
0
c
0
value is high are
referred to as convex shapes. Similarly, semi-convex and concave shapes are defined.
For each type of shape, three values for S
0
were chosen. For each value of S
0
,
three values for k were selected. For each set of values, six random simulations were
performed, in order to achieve statistical significance.
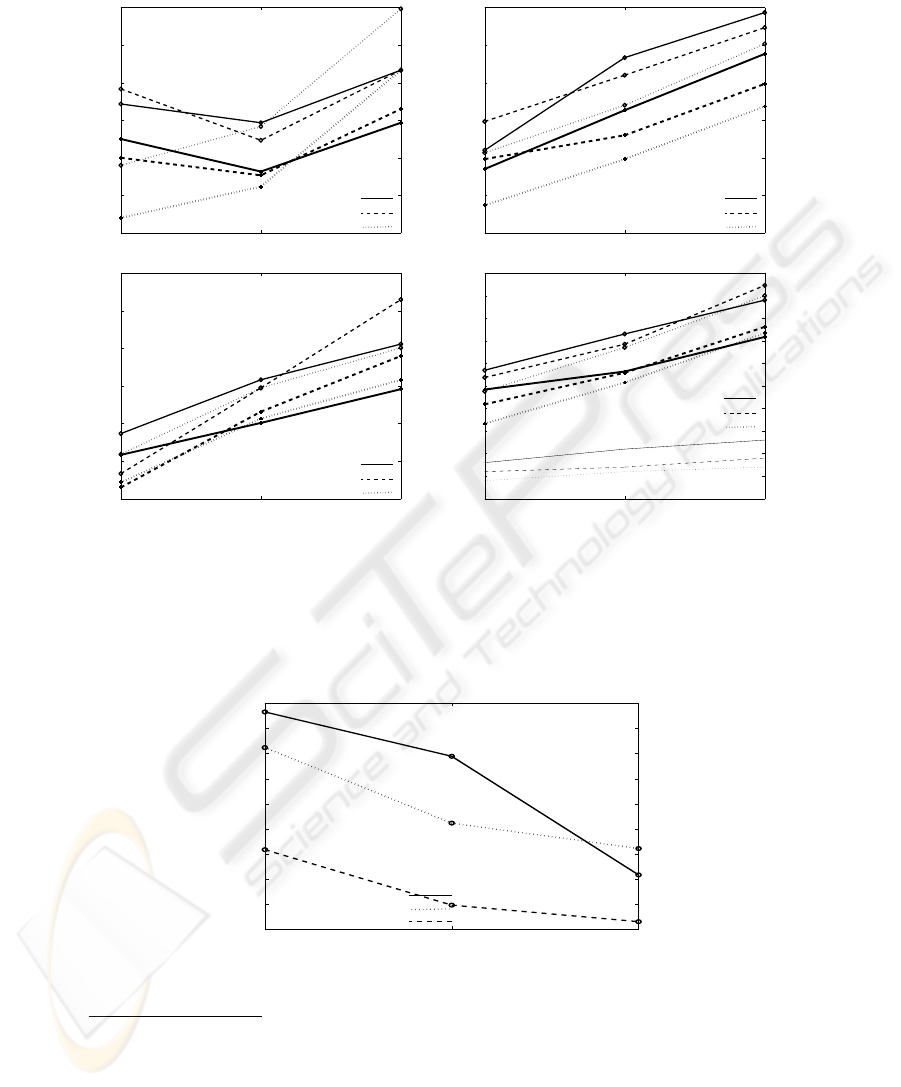
Figure 1 presents the results of the simulations, including the predictions of the
lower bound presented in equation 2. Note that although the sub-optimal cleaning al-
gorithm achieves results which are roughly 400% slower than the estimations of the
lower bound, the optimal algorithm achieves results which are also relatively far from
the lower bound’s estimations. This demonstrates the fact that the sub-optimal algo-
rithm’s performance are in fact, much closer to the optimal performances than expected
initially in [2].
After analyzing the results and trying to find a correlation between the number of
agents to the
perf ormance
optimal
perf ormance
sub−optimal
ratio, it seems that such correlation does not exist.
However, when focusing on the largest number of agents examined (8 agents), it can
be seen that as the size of F
0
gets bigger, the
perf ormance
optimal
perf ormance
sub−optimal
ratio gets smaller.
This holds for all three types of shapes. The meaning of this observation is that as the
problem is getting harder (larger initial shapes and more agents), the benefit from using
an optimal algorithm reduces (meaning, the sub-optimal algorithm achieves better and
better results). This is demonstrated in figure 2.
6 Symmetric Environments
In this section we shall present several comparisons of the SWEEP sub-optimal al-
gorithm and our optimal algorithm, in geometrical symmetric environments. Figure 3
presents the symmetric initial shapes chosen for this comparison. Four agents were
placed in symmetric places along the shapes, and both algorithms were tested.
30 40 50
10
15
20
25
30
35
40
Size of contaminated shape
Time steps
4 agents
6 agents
8 agents
Convex Shapes
30 40 50
10
15
20
25
30
35
40
Size of contaminated shape
Time steps
4 agents
6 agents
8 agents
Semi−Convex Shapes
30 40 50
20
30
40
50
60
70
80
Size of contaminated shape
Time steps
4 agents
6 agents
8 agents
Concave Shapes
30 40 50
0
5
10
15
20
25
30
35
40
45
50
Size of contaminated shape
Time steps
4 agents
6 agents
8 agents
Average
Fig.1. Comparison of sub optimal and optimal algorithms. The lower and thicker three lines rep-
resent the cleaning time of the optimal algorithm whereas the upper lines represent the SWEEP
cleaning algorithm’s performance. In the right chart on the bottom, the lower three lines represent
the lower bound of the optimal solution, as appears in equation 2.
30 40 50
1.15
1.2
1.25
1.3
1.35
1.4
1.45
1.5
1.55
1.6
Size of contaminated shape
Optimal / Sub−Optimal
Convex Shapes
Concave Shapes
Semi Convex Shapes
Optimality Ratio
(8 Agents)
Fig.2. Comparison of sub optimal and optimal algorithms. The Y -axes represents the
perf ormance
optimal
perf ormance
sub−optimal
ratio for various sizes. Note that as the problem gets bigger, the sub-
optimal performance of the algorithm gets closer to those of the optimal algorithm.
Fig.3. Symmetric initial shapes referred to as Shape-I, Shape-II and Shape-III respectively (left
shape is Shape-I).
Shape−I Shape−II Shape−III
0
50
100
150
200
250
300
350
400
450
Cleaning Time
Fig.4. Comparison of sub optimal and optimal algorithms. As can be seen once again, the per-
formance of the sub-optimal algorithm are only roughly 60% worse than those of the optimal
algorithm.
The comparison between the cleaning time of the optimal and sub-optimal algo-
rithms are presented in figure 4.
It is interesting to state that although the SWEEP algorithm, according to its defin-
ition, generates a symmetric behavior of the agents (meaning, the agents are traversing
the shape in the same manner, creating symmetric effects over it) this is not the case for
the optimal algorithm. Counter-intuitively, the optimal algorithm generates a remark-
ably non-symmetric behavior. The agents are divided into non-identical and non-stable
groups, while the effects the activities of the agents have on the shape transform it
quickly into a truly non-symmetric shape. Interestingly enough, this behavior occurs in
all three shapes (as well as in other symmetric shapes).
This insightful observation may lead to a change in the concepts which shape the
design of swarm algorithms in the future. Hitherto, it seems that most such works tend
to be biased by the belief that symmetric behavior generates high quality results while
being implemented into swarms’ behavior. Nevertheless, by ignoring this miss-belief,
an improvement in the performance of such algorithms may be achieved.
The reason for this may rely in low robustness of symmetric behaviors, which are
prone to “error resonance”, meaning — significantly increasing the effect of a small
error embedded within the swarm’s algorithm. By intentionally avoiding a symmetric
behavior, such traps may also be avoided, increasing the swarm’s robustness and sub-
sequently, its performance.
A demonstration of the above appears in figure 5.

Fig.5. The upper drawings demonstrate the symmetric nature of the SWEEP algorithm, while
the lower drawings demonstrate the non-symmetric behavior that was shown to be optimal for
Shape-II.
References
1. Vincent, P., Rubin, I.: “A Framework and Analysis for Cooperative Search Using UAV
Swarms”, ACM Simposium on applied computing, (2004).
2. Altshuler, Y., Bruckstein, A.M., Wagner, I.A.: “Swarm Robotics for a Dynamic Cleaning
Problem”, in “IEEE Swarm Intelligence Symposium 2005”, pp. 209–216, (2005).
3. Henrich, D.: “Space Efficient Region Filling in Raster Graphics”, The Visual Computer, pp.
10:205–215, Springer-Verlag, (1994).
4. Polycarpou, M., Yang, Y. and Passino, K.: “A Cooperative Search Framework for Distributed
Agents”, In Proceedings of the 2001 IEEE International Symposium on Intelligent Control
(Mexico City, Mexico, September 5–7). IEEE, New Jersey, 1–6, (2001).
5. Koenig, S., Liu, Y.: “Terrain Coverage with Ant Robots: A Simulation Study”, AGENTS’01,
May 28–June 1, Montreal, Quebec, Canada, (2001).
6. Rekleitisy, I., Lee-Shuey, V., Peng Newz, A., Chosety, H.: “Limited Communication, Multi-
Robot Team Based Coverage”, Proceedings of the 2004 IEEE International Conference on
Robotics and Automation, New Orleans, LA, April, (2004).
7. B.P.Gerkey, M.J.Mataric: “Sold! Market Methods for Multi-Robot Control”, IEEE Transac-
tions on Robotics and Automation, Special Issue on Multi-robot Systems, (2002).
8. G.Rabideau, T.Estlin, T.Chien, A.Barrett: “A Comparison of Coordinated Planning Methods
for Cooperating Rovers”, Proceedings of the American Institute of Aeronautics and Astro-
nautics (AIAA) Space Technology Conference, (1999).
9. S.M.Thayer, M.B.Dias, B.L.Digney, A.Stentz, B.Nabbe, M.Hebert: “Distributed Robotic
Mapping of Extreme Environments”, Proceedings of SPIE, Vol. 4195, Mobile Robots XV
and Telemanipulator and Telepresence Technologies VII, (2000).

10. M.P.Wellman, P.R.Wurman: “Market-Aware Agents for a Multiagent World”, Robotics and
Autonomous Systems, Vol. 24, pp.115–125, (1998).
11. R.Zlot, A.Stentz, M.B.Dias, S.Thayer: “Multi-Robot Exploration Controlled By A Market
Economy”, Proc. of the IEEE International Conference on Robotics and Automation, (2002).
12. D.Chevallier, S.Payandeh: “On Kinematic Geometry of Multi-Agent Manipulating System
Based on the Contact Force Information”, The 6
th
International Conference on Intelligent
Autonomous Systems (IAS-6), pp.188–195, (2000).
13. R.C.Arkin: “Integrating Behavioral, Perceptual, and World Knowledge in Reactive Naviga-
tion”, Robotics and Autonomous Systems, 6:pp.105-122, (1990).
14. M.Benda, V.Jagannathan, R.Dodhiawalla: “On Optimal Cooperation of Knowledge
Sources”, Technical Report BCS-G2010-28, Boeing AI Center, August (1985).
15. H.Bojinov, A.Casal, T.Hogg: “Emergent Structures in Moduluar Self-Reconfigurable Ro-
bots”, In Proceedings of the IEEE International Conference on Robotics and Automation,
pp.1734-1741, (2000).
16. R.A.Brooks: “A Robust Layered Control System for a Mobile Robot”, IEEE Journal of Ro-
botics and Automation, RA-2(1):14-23, March (1986).
17. A.Castano, R.Chokkalingam, P.Will: “Autonomous and Self-Sufficient CONRO Modules for
Reconfigurable Robots”, In Proceedings of the Fifth International Symposium on Distributed
Autonomous Robotic Systems (DARS 2000), pp. 155-164, (2000).
18. J.Deneubourg, S.Goss, G.Sandini, F.Ferrari, P.Dario: “Self-Organizing Collection and Trans-
port of Objects in Unpredictable Environments”, In Japan-U.S.A. Symposium on Flexible
Automation, pp.1093-1098, Kyoto, Japan, (1990).
19. A.Drogoul J.Ferber: “From Tom Thumb to the Dockers: Some Experiments With Foraging
Robots”, In Proceedings of the Second International Conference on Simulation of Adaptive
Behavior, pp.451-459, Honolulu, Hawaii, (1992).
20. D.Fox, W.Burgard, H.Kruppa, S.Thrun: “Collaborative Multi-Robot Exploration”, Au-
tonomous Robots, 8(3):325-344, (2000).
21. T.Haynes, S.Sen: “Evolving Behavioral Strategies in Predators and Prey”, Gerard Weiss and
Sandip Sen, Adaptation and Learning in Multi-Agent Systems, pp.113-126. Springer, (1986).
22. M.J.Mataric: “Designing Emergent Behaviors: From Local Interactions to Collective Intel-
ligence”, J.Meyer, H.Roitblat, and S.Wilson, Proc. the Second International Conference on
Simulation of Adaptive Behavior, pp.432-441, Honolulu, Hawaii, MIT Press, (1992).
23. D.Rus, B.Donald, J.Jennings: “Moving Furniture with Teams of Autonomous Robots”, Proc.
IEEE/RSJ International Conference on Intelligent Robots and Systems, pp.235-242, (1995).
24. D.Stilwell, J.Bay: “Toward the Development of a Material Transport System Using Swarms
of Ant-Like Robots”, In Proceedings of IEEE International Conference on Robotics and
Automation, pp.766-771, Atlanta, GA, (1993).
25. Z.Wang, Y.Kimura, T.Takahashi, E.Nakano: “A Control Method of a Multiple Non-
Holonomic Robot System for Cooperative Object Transportation”, Proc. Fifth International
Symposium on Distributed Autonomous Robotic Systems (DARS), pp.447-456, (2000).
26. E.Yoshida, S.Murata, S.Kokaji, K.Tomita, H.Kurokawa: “Micro Self-Reconfigurable Ro-
botic System Using Shape Memory Alloy”, In Proceedings of the Fifth International Sym-
posium on Distributed Autonomous Robotic Systems (DARS 2000), pp.145-154, (2000).
27. R.Madhavan, K.Fregene, L.E.Parker: “Distributed Heterogenous Outdoor Multi-Robot Lo-
calization”, In the proceedings of IEEE International Conference on Robotics and Automa-
tion (ICRA), pp.374–381, (2002).
28. Hart, P.E., Nilsson, N.J., Raphael, B.: “A formal basis for the heuristic determination of
minimum cost paths”, IEEE Transactions on Systems Science and Cybernetics 4(2): 100–
107, (1968).
