
MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME
HUMANOID MOTION GENERATION
Doik Kim, Youngjin Choi, and ChangHwan Kim
Intelligent Robotics Research Center
Korea Institute of Science and Technology (KIST)
39-1 Hawolgok-dong, Seongbuk-gu, Seoul 136-791, Korea
Keywords:
Humanoid, COG, COG Jacobian, Balancing, Motion Generation.
Abstract:
For a legged robot such as a humanoid, balancing its body during a given motion is natural but the most impor-
tant problem. Recently, a motion given to a humanoid is more and more complicated, and thus the balancing
problem becomes much more critical. This paper suggests a real-time motion generation algorithm that guar-
antees a humanoid to be balanced during implementing a given motion. A desired motion of each arm and/or
leg is planned by the conventional motion planning method without considering the balancing problem. In
order to balance a humanoid, all the given motions are embedded into the COG Jacobian. The COG Jaco-
bian is modified to include the desired motions and, as a result, dimension of the COG Jacobian is drastically
reduced. With the motion-embedded COG Jacobian, balancing and performing a task is completed simultane-
ously, without changing any other parameters related to the control or planning. Validity and efficiency of the
proposed motion-embedded COG Jacobian is simulated in the paper.
1 INTRODUCTION
A high mobility of a humanoid makes it difficult to
generate a motion and to interact with environment in
real time. Many previous works in motion generation
of a humanoid is to replay a pre-defined joint motion
and modify it little by a certain control method in real
situation. (Yamaguchi et al., 1999; Nagasaka et al.,
2004) For a complicated, smooth and agile motion, it
is necessary to develop a real time motion generating
method. In addition, it is desired to include dynam-
ics to improve the stability of a humanoid. Dynam-
ics, however, requires a large amount of computation.
The center of gravity(COG) can be a simple alterna-
tive of full dynamics, since it can be treated as a usual
kinematics which needs less computation than that of
dynamics, and ,furthermore, it reflects dynamic prop-
erties such as the mass and the mass center. Thus, the
COG is the important property which relates to the
stability, motion, and dynamics.
In order to use the COG relation in motion gen-
eration, the COG Jacobian is needed. The COG Ja-
cobian is firstly proposed by Kagami, et al, in 2000,
but they developed a numerical method(Kagami et al.,
2000). An analytic formulation of the COG Jaco-
bian is proposed by Sugihara, et al, in 2002(Sugihara
et al., 2002; Sugihara and Nakamura, 2002). They
used the COG Jacobian as follows: At first, the ZMP
trajectory is predefined and it is used as a desired mo-
tion of the COG Jacobian. Motions of some limbs are
used as constraints. An optimization problem that sat-
isfies the COG Jacobian and given constraints simul-
taneously, are solved to generate joint motion. As an
application, Sugihara, et al, used the COG Jacobian
for whole body cooperative balancing(Sugihara and
Nakamura, 2002), but the method needs large com-
putation in optimization.
The method proposed in this paper is that all the
given motions are embedded in the COG Jacobian to
generate joint motions in real time. In order to em-
bed motions into the COG Jacobian, a humanoid is
divided into several sections. A motion of each sec-
tion is considered independently, and relations of each
independent motion are combined with the motion-
embedded COG Jacobian. The dimension of the mod-
ified COG Jacobian and the number of constraints are
reduced drastically, since motions are considered in-
dependently. In addition, the modified COG Jacobian
guarantees the balancing a humanoid and performing
a task.
This paper is organized as follows: Section 2 de-
scribes the overall system. Section 3 introduces
55
Kim D., Choi Y. and Kim C. (2005).
MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 55-61
DOI: 10.5220/0001187500550061
Copyright
c
SciTePress

the COG Jacobian suggested by Sugihara, et al, in
2002(Sugihara et al., 2002; Sugihara and Nakamura,
2002). Section 4 derives the motion-embedded COG
Jacobian. Section 5 simulates the suggested algo-
rithm, and section 6 concludes the paper.
2 OVERALL SYSTEM
For a human, if arms do a certain task, they focus on
the task not on the balancing. The remaining parts of
the human balance its body regardless of the task. The
proposed method, i.e., the motion-embedded COG Ja-
cobian, implements the fact. Consequently, when we
plan a motion, balancing problem does not need to be
considered, and furthermore, a conventional motion
planning method can be applied without any modifi-
cation.
Desired COG-ZMP
Desired Arm & Leg
Motion
COG-ZMP Control
Motion Control
Inverted Pendulum Model
Motion Embedded
COG Jacobian
Joint Control
Humanoid
Angle
Real COG
& ZMP
Real Arm & Leg
Motion
Figure 1: Humanoid Control Flow
The overall control scheme can be divided into two
major categories: 1) COG and ZMP related algo-
rithms and 2) motion related algorithms. The COG-
ZMP related algorithms are based on the inverted
pendulum model
1
and the motion related algorithms
focus on how to distribute the COG-ZMP profile
and given task motion to each joint with guaranteing
the balancing and performing the given task motion.
Fig. 1 shows the overall control flow.
For the stability of a humanoid, the COG-ZMP pro-
file is predefined for several basic motion, for ex-
ample, forward/backward movement, side movement
and turning. The COG-ZMP profile is derived from
the inverted pendulum model, which gives relatively
simple relation. COG is calculated from the internal
1
In this paper, we don’t include the planning of COG
and/or ZMP. You can find this subject in references(Hirai
et al., 1998; Choi et al., 2004).
joint information, thus it represents the pose of a hu-
manoid. ZMP is an dynamic property that represents
the stability whether a humanoid is to be rollover or
not. Two properties are tightly related, and therefore,
the predefined COG-ZMP are controlled simultane-
ously with real COG and ZMP, in order to guarantee
the pose and the stability.
Figure 2: Mahru
Before developing the motion-embedded COG Ja-
cobian, a humanoid is divided into several parts. A
humanoid has four limbs attached at the main body.
Hereafter, each limb and the main body will be called
a section. For a human, a task is done with some sec-
tions, usually two arms, and balance the body with
other sections, usually two legs. It means that not
all sections are dedicated into one task, but they do
their own tasks, for example, balancing or a given
task. Thus the motion of each section can be given
independently. According to the existence of a given
desired motion, the section is classified into the idle
section and the busy section: the idle section has no
given motion and the busy section has a given mo-
tion. If a section has zero motion, i.e., it is fixed at
current position, it can be considered as an idle sec-
tion or a busy section. In most case, a supporting sec-
tion which is attached on the ground are considered
as a busy section, since they have a role of balanc-
ing the body. A given motion of each limb or a main
body can be given as a joint motion and/or a Carte-
sian motion. If a busy section has a given motion in
the Cartesian space, it will be called C-busy section
ICINCO 2005 - ROBOTICS AND AUTOMATION
56
and a section with a given motion in the joint space
is J-busy section. Motion control step in Fig. 1 is
done for a C-busy section. A J-busy section will be
controlled at the joint control step.
The given motion and corresponding COG-ZMP
profile are distributed to joints of a humanoid by us-
ing the COG Jacobian, i.e., the motion of the inverted
pendulum model is transformed into the motion of a
complicated multi-body model. By using the motion-
embedded COG Jacobian, the stability and a given
motion are guaranteed simultaneously.
The algorithm suggested in this paper is applied to
the humanoid, Mahru, developed at IRRC(Intelligent
Robotics Research Center), KIST in 2004 shown in
Fig. 2. Mahru has the height of about 150cm, and
the weight is about 67kg. It has 6-dof for each legs
and arms, 1-dof for the waist, 2-dof for the neck, and
each hand has 4-dof. In total, it has 35-dof. A stereo
camera is equipped.
3 COG JACOBIAN
2
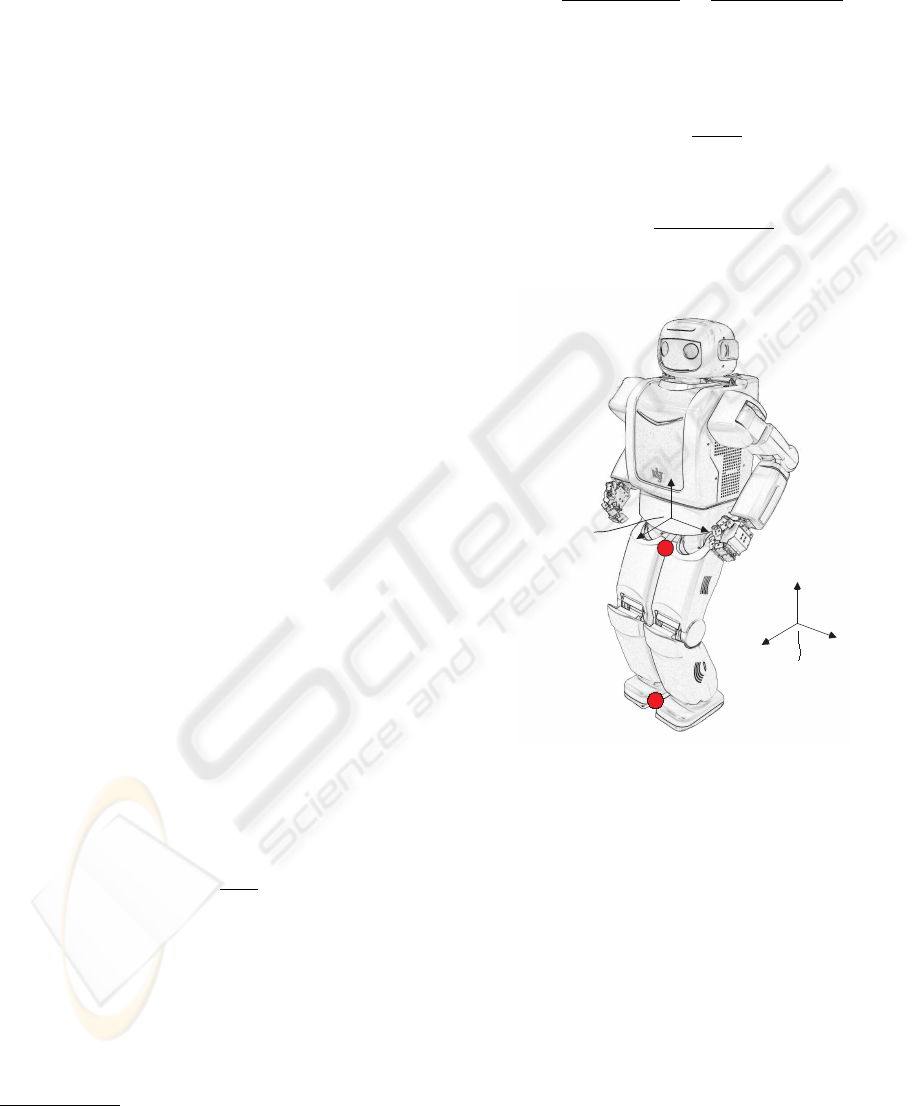
Let us consider a n-DOF humanoid. There are two
referential frames to describe a humanoid as shown in
Fig. 3. The world coordinate frame is fixed on some-
where in the world and represents the global motion
of a humanoid. The body center frame is fixed on a
humanoid to describe the local motion. Almost all
the properties of a humanoid is described in the body
center frame. The leading superscript
o
(·) implies that
the elements are represented in the body center frame,
and without it, a value is based on the world coordi-
nate frame.
The COG, p
G
, of a humanoid is a function of joint
angle vector, q, i.e., p
G
= f(q). Thus, there exists a
Jacobian J
G
which can relate
˙
q to
˙
p
G
as:
˙
p
G
= J
G
˙
q (1)
where the (3 × n) matrix J
G
is defined by
J
G
≡
∂p
G
∂q
(2)
We call J
G
the COG Jacobian hereafter. p
G
is a quite
complex function with multiple arguments. Kagami,
et al, proposed the numerical method to calculate
it(Kagami et al., 2000), which unfortunately needs
a large amount of computation. Sugihara, et al, de-
veloped a fast and accurate calculation method of J
G
with the following approach(Sugihara et al., 2002).
2
This section is borrowed from Sugihara, et
al,(Sugihara et al., 2002; Sugihara and Nakamura,
2002).
Firstly, the relative COG velocity with respect to
the body center frame,
o
˙
p
G
, can be expressed as:
o
˙
p
G
=
P
n−1
i=0
m
i
o
˙
r
G
i
P
n−1
i=0
m
i
=
P
n−1
i=0
m
i
o
J
G
i
˙
q
P
n−1
i=0
m
i
(3)
where m
i
is the mass of link i,
o
r
G
i
is the position of
the center of mass of link i with respect to the body
center frame, and
o
J
G
i
(3 × n) is defined by
o
J
G
i
≡
∂
o
r
G
i
∂q
(4)
Therefore, Jacobian
o
J
G
which relates
˙
q to
o
˙
p
G
is
o
J
G
=
P
n−1
i=0
m
i
o
J
G
i
P
n−1
i=0
m
i
(5)
Body Center
Frame
COG
X
Y
Z
World Coorinate
Frame
ZMP
Figure 3: Coordinate System of Mahru
Secondly, suppose link 1 is the base section, which
is fixed in the world frame (for example, when the
right leg is the supporting leg, the right leg is fixed on
the ground and becomes the base section), the COG
velocity with respect to the world coordinates frame,
˙
p
G
is
˙
p
G
=
˙
p
o
+ ω
o
× R
o
o
p
G
+ R
o
o
˙
p
G
=R
o
{
o
˙
p
G
−
o
˙
p
1
+ (
o
p
G
−
o
p
1
) ×
o
ω
1
}
=R
o
o
J
G
˙
q
+ R
o
{−
o
J
v
1
+ [(
o
p
G
−
o
p
1
)×]
o
J
ω
1
}
˙
q
1
(6)
where p
o
is the position of the body center, ω
o
is the
angular velocity of the body center, and R
o
is the at-
titude matrix of the body center with respect to the
MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION
57

world frame.
o
p
1
is the position of the base section,
o
ω
1
is the angular velocity of the base section,
o
J
v
1
is
the linear velocity part of the base Jacobian and
o
J
ω
1
is the angular velocity part of the base Jacobian with
respect to the body center frame. [v×] means outer-
product matrix of a vector v (3 × 1).
˙
q
i
is the joint
velocity of section i. Note that the base section can be
any section that is fixed on the ground, but here, we
assigned the base section with the number 1 without
loss of generality.
In order to use Eq. (6) in the following section, it is
rewritten here as:
˙
p
G
=
m
X
i=1
R
o
o
J
G
i
˙
q
i
+ R
o
{−
o
J
v
1
+ [(
o
p
G
−
o
p
1
)×]
o
J
ω
1
}
˙
q
1
(7)
where m is the number of sections.
Now, let us derive the motion-embedded COG Ja-
cobian from Eq. (7).
4 MOTION-EMBEDDED COG
JACOBIAN
4.1 Embedment of J-Busy Section
It is easy to embed a joint motion into the COG Jaco-
bian, since the joint motion can be directly replaced
˙
q
i
in Eq. (7).
If section j is a J-busy section, Eq. (7) becomes
˙
p
G
− R
o
o
J
G
j
˙
q
j
=
m
X
i=1,i6=j
R
o
o
J
G
i
˙
q
i
+ R
o
{−
o
J
v
1
+ [(
o
p
G
−
o
p
1
)×]
o
J
ω
1
}
˙
q
1
(8)
The second term of the left hand side compensates
the motion of the jth section. Therefore, the other
sections shown in the right hand side can generate a
joint motion with the compensated COG motion.
If at least one section, i.e., the base section, is an
idle section, then Eq. (8) can compensate motions of
the other sections. If all sections are the J-busy sec-
tion, there is no section to compensate given motions.
In this case, an optimization method needs to be ap-
plied.
4.2 Embedment of C-Busy Section
Let us derive the motion-embedded COG Jacobian for
the C-busy section. Each section of a humanoid is
considered as an independent section, i.e., any section
can have its own motion independently without con-
sidering other sections. In general, the i-th section has
the following relation:
o
˙
x
i
=
o
J
i
˙
q
i
(9)
where
o
˙
x
i
= [
o
˙
p
T
i
;
o
ω
T
i
]
T
is the end point velocity of
the section,
o
˙
p
i
and
o
ω
i
are the linear and the angular
velocity, respectively.
˙
q
i
is the joint velocity, and
o
J
i
is the usual Jacobian matrix represented in the body
center frame.
In our case, the body center is floating, and thus the
end point motion about the world coordinate frame is
written as follows:
˙
x
i
= X
−1
i
˙
x
o
+ X
o
o
˙
x
i
(10)
where
˙
x
o
= [
˙
p
o
T
; ω
o
T
]
T
is the velocity of the body
center represented in the world coordinate system,
and
X
i
=
I
3
[R
o
o
r
i
×]
0
3
I
3
(11)
is a (6 × 6) matrix which relates the body center ve-
locity and the end point velocity of the i-th section.
I
3
and 0
3
are the (3 × 3) identity and zero matrix,
respectively. R
o
is the orientation of the body center
based on the world coordinate system.
o
r
i
is the posi-
tion vector from the body center to the end of the i-th
section based on the body center frame. The transfor-
mation matrix X
o
is
X
o
=
R
o
0
3
0
3
R
o
. (12)
By combining Eq. (9) and Eq. (10), the end point
velocity based on the world coordinate system is
˙
x
i
= X
−1
i
˙
x
o
+ X
o
o
J
i
˙
q
i
(13)
For simplicity, we will use the relation J
i
=
X
o
o
J
i
, hereafter.
From Eq. (13), we can see that all sections should
satisfy the compatibility condition, i.e., the body cen-
ter velocity,
˙
x
o
, in Eq. (13) for each section is the
same, so that sections are connected without being
broken., and thus arbitrary two sections, for example,
the i-th and j-th section should satisfy the following
relation:
X
i
(
˙
x
i
− J
i
˙
q
i
) = X
j
(
˙
x
j
− J
j
˙
q
j
). (14)
From Eq. (14), the joint velocity of any section can
be represented by the joint velocity of any other sec-
tion. However, all sections will be represented by the
base section, since the motion of the body center is
represented by the base section, as shown in Eq. (7).
The base section can be the supporting leg in the sin-
gle supporting phase or one of both legs in the double
supporting phase if a humanoid is standing. Let us
ICINCO 2005 - ROBOTICS AND AUTOMATION
58

express the base section with the subscript 1, then the
joint velocity of any section is expressed as:
˙
q
i
= J
−1
i
˙
x
i
− J
−1
i
X
i1
(
˙
x
1
− J
1
˙
q
1
), (15)
for i = 2, · · · , m, where m is the number of sections.
Here,
X
i1
=
I
3
[R
o
(
o
r
i
−
o
r
1
)×]
0
3
I
3
. (16)
Note that if a section is a redundant system, any null
space optimization scheme can be added in Eq. (15),
and J
−1
i
becomes a generalized inverse.
By substituting Eq. (15) into Eq. (7), the motion-
embedded COG Jacobian relation becomes
˙
p
G
= R
o
{−
o
J
v
1
+ [(
o
p
G
−
o
p
1
)×]
o
J
ω
1
}
˙
q
1
+
m
X
i=1
R
o
o
J
G
i
J
−1
i
(
˙
x
i
− X
i1
˙
x
1
)
+
m
X
i=1
R
o
o
J
G
i
J
−1
i
X
i1
J
1
˙
q
1
(17)
where J
v
1
= R
o
o
J
v
1
and J
ω
1
= R
o
o
J
ω
1
are the
linear and angular velocity part of the base section
Jacobian. Note that if i = 1,
˙
x
i
− X
i1
˙
x
1
= 0 and
R
o
o
J
G
i
J
−1
i
X
i1
J
1
˙
q
1
= R
o
o
J
G
i
˙
q
1
.
Finally, all desired motions,
˙
x
i
, are embedded in
the modified COG Jacobian. Thus the effect of the
COG movement generated by the desired motion is
compensated by the base section. Eq. (17) can be
rewritten like the usual kinematic Jacobian of the base
section:
˙
p
meG
= J
meG
˙
q
1
(18)
where
˙
p
meG
=
˙
p
G
−
m
X
i=1
R
o
o
J
G
i
J
−1
i
(
˙
x
i
− X
i1
˙
x
1
), (19)
J
meG
= R
o
{−
o
J
v
1
+ [(
o
p
G
−
o
p
1
)×]
o
J
ω
1
}
+
m
X
i=1
R
o
o
J
G
i
J
−1
i
X
i1
J
1
. (20)
The modified COG motion,
˙
p
meG
, consists of two
relations: a desired COG motion(the first term) and
the relative effect of motions of each section(the sec-
ond term). The modified COG Jacobian, J
meG
also
consists of two relations: the effect of the body cen-
ter(the first term) and the effect of motions of each
section(the second term).
The modified COG Jacobian J
meG
is a (3 × n
1
)
matrix where n
1
is the dimension of the base sec-
tion, which is smaller than that of the original COG
Jacobian. For example, Mahru in Fig. 2 has a 6-dof
leg, and thus n
1
= 6 if the leg is the base section.
After solving Eq. (18), the joint motion of the base
section is obtained. The resulting base section mo-
tion balances a humanoid robot automatically during
the movement of all other sections. With the resulting
joint motion of the base section, the joint motion of all
other sections are obtained by Eq. (15). The resulting
motion follows the desired motion, regardless of the
balancing motion of the base section.
5 SIMULATION
In order to show the validity of the suggested algo-
rithm, a dynamic simulator developed at IRRC, KIST
is used. The simulator can simulate a humanoid
Mahru shown in Fig. 2.
To show the effect of the J-busy and C-busy sec-
tion, simultaneously, two arms are J-busy and two
legs are C-busy. The left and right foot is moved
up and down, in turn, with a sinusoidal function.
Two motions for arms are given: 1) both arms are
stretched forward as shown in Fig. 4 and 2) the right
arm is raised and waves it shown in Fig. 5. The de-
sired arm motions are obtained by the motion cap-
tured data(Kim et al., 2005). In order to move the
COG to the center of the supporting foot, a predefined
COG-ZMP trajectory is applied.
The first motion, stretching two arms forward, can
make the humanoid fall down since the mass center is
moved in front of the humanoid. By using the motion-
embedded COG Jacobian, the desired motion of arms
are compensated by the supporting leg, and thus the
leg moves the humanoid body back automatically as
shown in Fig. 4 (b), the side view.
The second motion, rasing and waving right hand,
makes a large disturbance to the humanoid since the
fast waving motion changes the mass center quickly
to the left and right. Thus if the right hand goes to the
right side when the right foot is off the ground, it is
difficult to move the COG and ZMP to the stable re-
gion, i.e., the left foot. However, the left leg compen-
sates the motions of arms by the motion-embedded
COG Jacobian, and consequently, the COG and ZMP
are still in the stable region as shown in Fig. 5.
The overall motions are complicated and it is easy
to make the humanoid unstable. However, by using
the motion-embedded COG Jacobian, any parameters
such as control gain, COG/ZMP trajectory, and etc,
do not need to be changed to stabilize or balance the
humanoid.
6 CONCLUDING REMARK
In this paper, a real-time motion generation method
for a humanoid is suggested. A desired motion of
each section is obtained by the conventional motion
MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION
59

planning method without considering the balancing
problem.
The method can balance a humanoid by using the
motion-embedded COG Jacobian, which reduces the
computation time to generate a motion and satisfies
the given motion and the balance, simultaneously.
Validity and efficiency of the suggested method is
examined by the simulation. Two motions are ap-
plied to the humanoid, and without changing any pa-
rameters on the control or planning, the humanoid ac-
complishes the given motions and it also balanced its
body.
In the paper, we assume that all the sections have
their own tasks. If a section does not have a desired
motion, i.e., an idle section, there are two possible
cases:
1. the idle section is considered as a busy section with
a zero motion, i.e., it is fixed at the current position.
In this case, the section is considered as a C-busy
section, and the method suggested in this paper can
be applied.
2. with some optimization scheme, the idle section is
used actively to balance the humanoid. Since the
idle section has no desired motion, by changing
its position actively, the humanoid can balance the
body more easily and naturally. The optimization
of the idle section is still under development.
REFERENCES
Choi, Y., You, B.-J., and Oh, S.-R. (2004). On the stability
of indirect ZMP controller for biped robot systems.
In International Conference on Intelligent Robots and
Systems, pages 1966–1971.
Hirai, K., Hirose, M., Haikawa, Y., and Takenaka, T. (1998).
The development of honda humanoid robot. In IEEE
International Conference on Robotics and Automa-
tion, pages 1321–1326, Leuven, Belgium.
Kagami, S., Kanehiro, F., Tamiya, Y., Inaba, M., and Inoue,
H. (2000). Autobalancer: An online dynamic balance
compensation scheme for humanoid robots. In The
4th International Workshop on Algorithmic Founda-
tion on Robotics (WAFR’00).
Kim, C.H., Kim, D., and Oh, Y. (2005). Solving an
inverse kinematics problem for a humanoid robot’s
imitation of human motions using optimization. In
ICINCO2005, (accepted).
Nagasaka, K., Kuroki, Y., Suzuki, S., Itoh, Y., and Yam-
aguchi, J. (2004). Integrated motion control for walk-
ing, jumping and running on a small bipedal enter-
tainment robot. In IEEE International Conference on
Robotics and Automation, pages 3189 – 3194.
Sugihara, T. and Nakamura, Y. (2002). Whole-body co-
operative balancing of humanoid robot using COG ja-
cobian. In International Conference on Intelligent Ro-
bots and Systems, pages 2575–2580, EPFL, Lausanne,
Swizerland.
Sugihara, T., Nakamura, Y., and Inoue, H. (2002). Realtime
humanoid motion generation through ZMP manipula-
tion based on inverted pendulum control. In IEEE In-
ternational Conference on Robotics and Automation,
pages 1404–1409, Washington, DC.
Yamaguchi, J., Soga, E., Inoue, S., and Takanishi, A.
(1999). Development of a bipedal humanoid robot —
control method of whole body cooperative dynamic
biped walking. In IEEE International Conference on
Robotics and Automation, pages 368–374.
ICINCO 2005 - ROBOTICS AND AUTOMATION
60

(a) front view
(b) side view
Figure 4: example 1: both arms move forward
(a) front view
(b) side view
Figure 5: example 2: right arm is raised and waves
MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION
61
