Neural Network Modeling for ALSTOM Gasifier

Armando Rivadeneyra Bardales

, Danilo Soares Barboza

, William Ipanaqué

Martin Flores

Universidad de Piura, Piura-Perú

Universidad de Santa Catarina, Brasil

Abstract. Neural Network Model Based Predictive Control (MPC) has become

a good choice of control strategy in many cases especially in the process

industry because it could face non linearities and cross coupling variables [6],

being modeling the first step to achieve this end. The model of a gasifier,

provided by ALSTOM Power Technology Centre, is of an industrial standard

and has been validated against a set of real data from test facilities. This makes

the challenge all the more relevant to practicing engineers. The paper sets out

the specifications and describes the design and performance of neural networks

modeling and presents a neural network approach to model the ALSTOM

Benchmark Challenge gasifier. This is a complex non-linear process, with a

high degree of cross coupling of the variables, manual control is difficult.

1 Introduction

Power generation is responsible for a significant part of the total emissions of solid,

liquid and gaseous pollutants all around the world. Due to a predicted higher long-

term availability of solid fuels, in particular coal, compared to oil and natural gas,

solid fuels will play an important part in future energy supply.

As a result of this, Integrated Gasification Combined Cycle (IGCC) power plants,

combining gasification with a gas and steam cycle, are being developed around the

world.

Low emission power generation techniques are being developed around the world

to provide environmentally clean and efficient power. To this scope, ALSTOM has

carried out researches on the combustion of pulverized coal using an Integrated

Gasification Combined Cycle (IGCC) power plant.

The operation of this Pilot Integrated plant (PIP) is based upon the Air Blown

Gasification Cycle (ABGC). First, limestone is added to the pulverized coal to

minimize sulphur originated from the coal.

Then, the mixture is fluidized in a stream of air and steam and conveyed into the

gasifier. As a result, a low calorific value fuel gas is produced by the reaction between

the air and steam and the carbon and volatiles from the coal. The limestone, ash and

unreacted carbon are removed as bed material from the base of the gasifier or

elutriated to avoid carrying it out of the top of the gasifier as fines with the product

gas.

Rivadeneyra Bardales A., Soares Barboza D., Ipanaqué W. and Flores M. (2005).

Neural Network Modeling for ALSTOM Gasiﬁer.

In Proceedings of the 1st International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 94-102

DOI: 10.5220/0001182600940102

 SciTePress

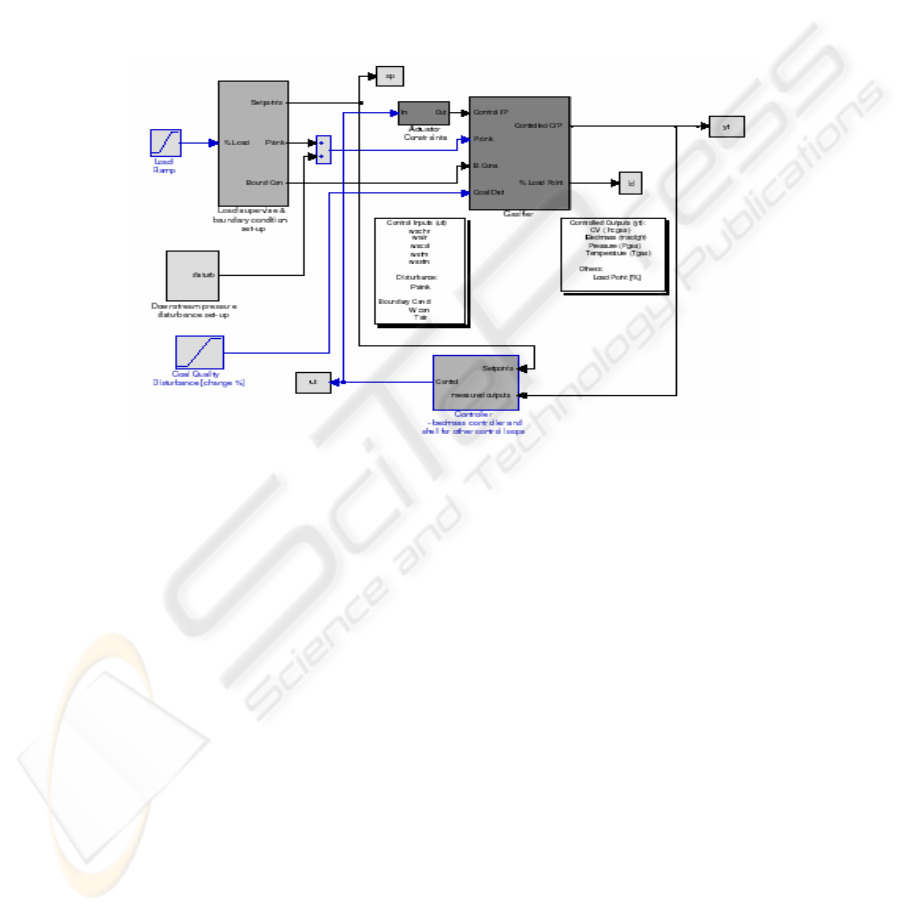
In 1997 the ALSTOM Power Technology Centre issued an open challenge to the

UK academic control community, which addressed the control of a Gasifier plant.

The 'Challenge information pack' included three linear models (derived from

ALSTOM's comprehensive non-linear model of the system), together with a detailed

specification comprising output limits, control input constraints and disturbance tests

[1] and [2].

The second round of the challenge was issued in June 2002 (see reference [3]), and

extends the original study by providing participants with the full non-linear model of

a gasifier in MATLAB\SIMULINK shown in Figure 1.

It includes an expanded specification to incorporate set point changes and coal

quality disturbances.

Fig. 1. MATLAB/SIMULINK model plant.

In this paper a practical design procedure of Neural Networks Dynamical

Modeling is studied and applied to a simulated non linear plant of gasifier.

The rest of this paper is organized as follows. Section 2 discusses modeling using

neural network and included a short summary about the gasifier. Also are explained in

section 2 data acquisition for identification and the simulation results obtained after

the neural model have determined, and finally in section 3 some conclusions are

drawn from work.

2 Modeling Using Neyral Network

Neural networks have found widespread application to solving modeling and global

optimization problems, and have been used for control of power systems. For further

control design using Model Based Predictive Control, we require to find a non linear

model for this purpose.

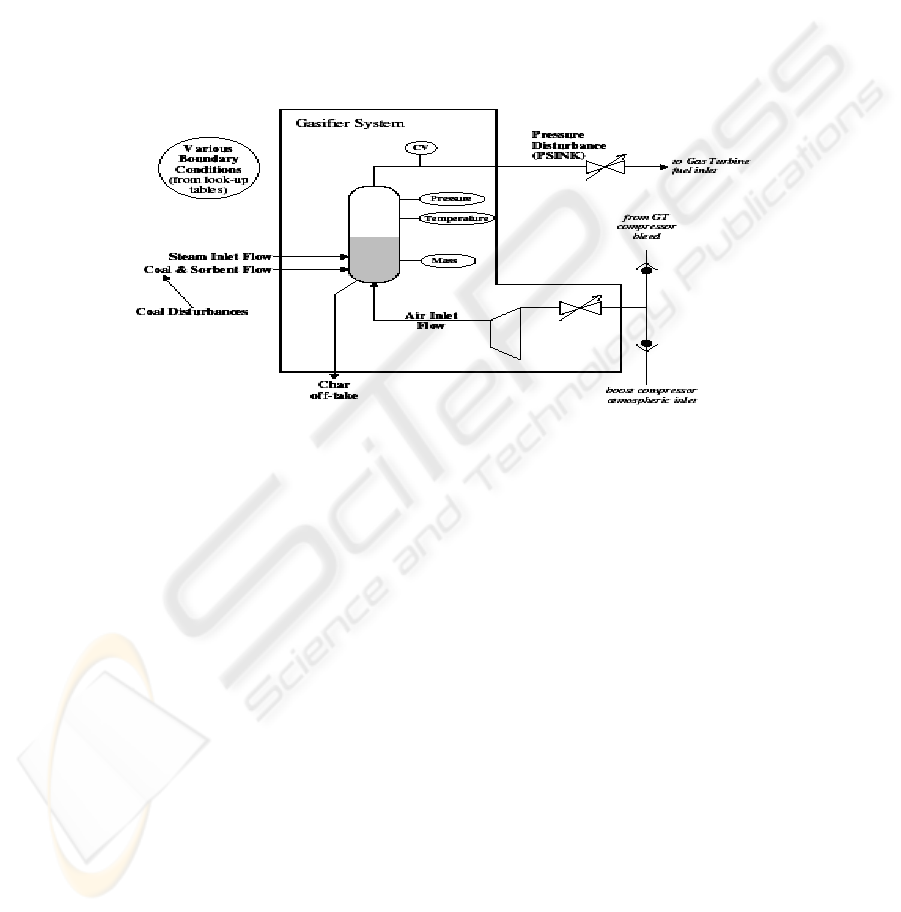
2.1 Plant Description

A schematic of the plant is shown in Figure 2. The gasifier is a non-linear,

multivariable component, having five controllable inputs (coal, limestone, air, steam

and char extraction) and four outputs (pressure, temperature, bed-mass and gas

quality) with a high degree of cross coupling between them.

Note that as limestone is used to absorb sulphur in the coal its flow rate must be set

to a fixed ratio of coal flow, nominally 1:10 limestone to coal. This leaves effectively

a four-input four-output regulation problem for the control design [4].

Other non-control inputs for the model include boundary conditions (to allow

maneuvers to different operating points), a disturbance input (PSINK) which

represents pressure disturbances, and a coal quality input.

Fig. 2. Gasifier Schematics.

The controllable inputs then are:

• Char extraction flow - WCHR (kg s-1)

• Air mass flow - WAIR (kg s-1)

• Coal flow - WCOL (kg s-1)

• Steam mass flow - WSTM (kg s-1)

The controlled outputs are:

• Fuel gas calorific value - CVGAS (J kg-1)

• Bed mass - MASS (kg)

• Fuel gas pressure - PGAS (N m-2)

• Fuel gas temperature - TGAS (K)

2.2 Data acquisition for the identification

The set of data to the training process and validation process were collected from the

model of the plant given by ALSTOM, after knowing the dynamics of the system and

after several testing process using a random signal as inputs within the measure of the

range of each input.

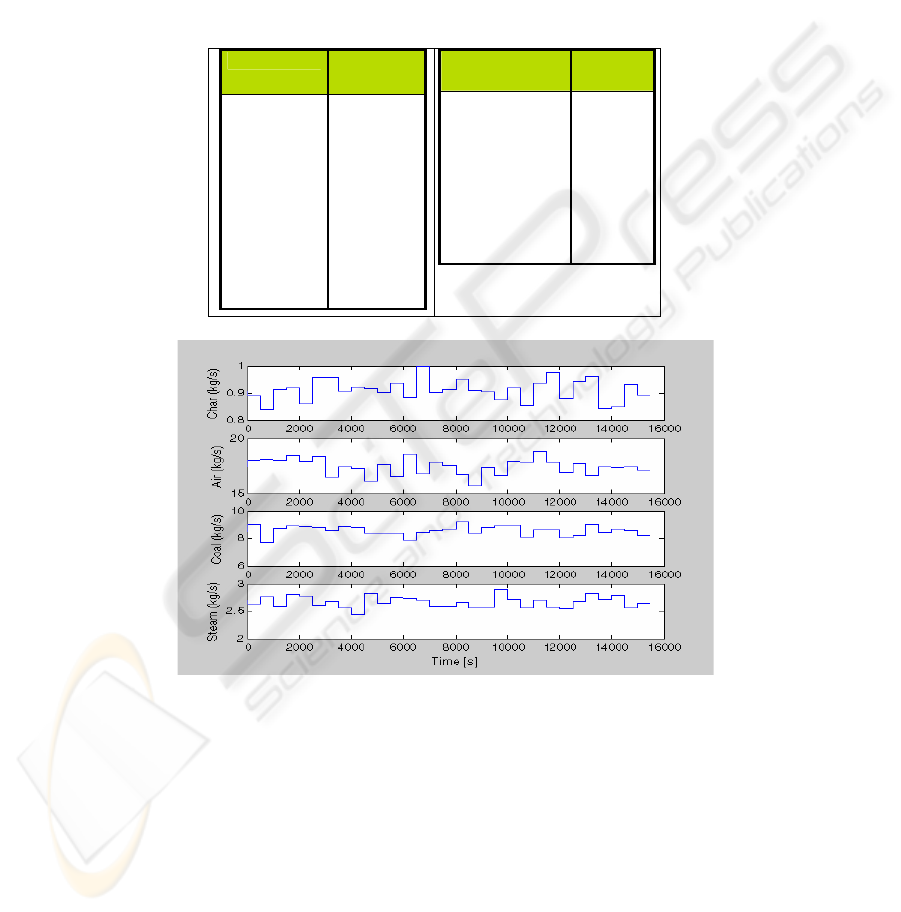
The type of input has suggested for the identification and validation of the model is

the PRS (Pseudo-random Signal), this is used for the design of experiments of

identification [5].

We will consider variations on every input of the gasifier. Figure 3 and 4 shows the

PRS inputs and the output for this signal respectively, where the dot line represents

their mean values shown in Table 1. This PRS takes randomic values, within 10%

range of the 100% load case for the gasifier, as inputs to the model plant and with the

result output data we got the set to train the network.

Table 1. Input and output var and its mean values.

Inputs Values

(kg/s)

WCHR 0.9

WAIR 17.42

WCOL 8.55

WSTM 2.70

WLS 0.85

Outputs Values

CVGAS

(J/kg)

4.36e+6

MASS (kg) 10000

PGAS(N/m

) 2.0e+6

TGAS (K) 1223.2

Fig. 3. Simulated PRS input.

Fig. 4. Simulated output for a PRS input.

As explained above limestone must be set to a fixed ratio of the coal flow,

nominally 1:10. This leaves effectively a four-input four-output regulation problem

for model design which simplifies the quantity of data needed to train the neural

network on the identification process.

2.3 Plant Identification

At first we need to define which kind of neural network we will use. As we move into

the neural network field we find that one of the most common network used in this

field to approximate a nonlinear continues function is the two layers perceptron [8],

being the first layer function sigmoid and the second layer function lineal as shown in

the Figure 5.

The number of units of the output layer is limited to the number of outputs, in this

case four and the number of units of the hidden layer can not be less than the number

of output units because they would be linearly dependent. After several tests we found

four units were a good choice.

Also as inputs we added one delayed output following observable states black box

equation showed below [7]:

Ec.1 Generalized model type input-output:

{}

)(),...1(),(),(),...1(),()1( mkukukunkykykyhky

−

(1)

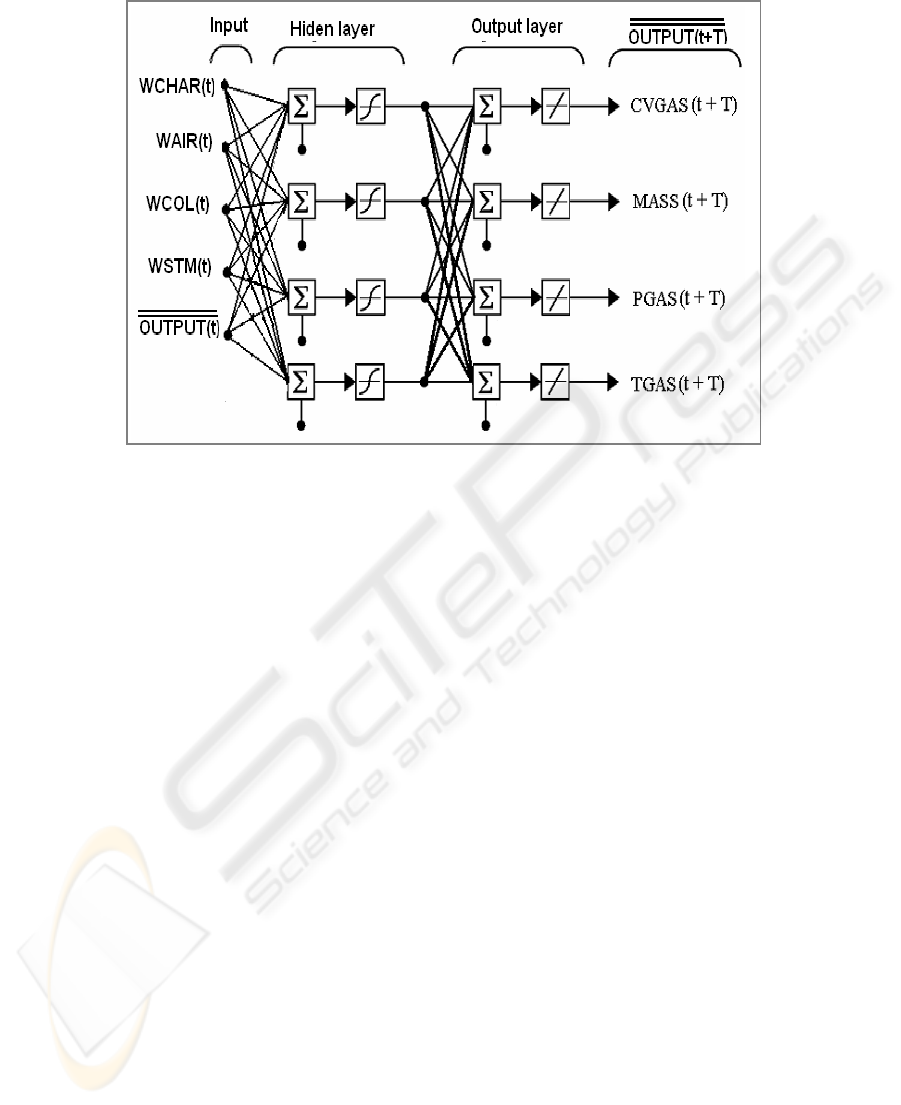
Fig. 5. Neural network schematics

We have included in our testing process more past output data using a delayed

network and organizing a past data set [8], but experimentally it did not improve the

performance of the network. As the simple network performance good enough, we

leave the attempts of using delayed networks.

This set of data collected were used for training and validating the neural network,

this is divided in two parts, first part for training and second one for validating. In

order to avoid square error function to minimize, as a priority, greater module signals

we have normalized all signals as in their original values these would have more

effect on the total value of the error. Normalization is hardly recommended by some

training algorithms [8].

Figures 6 shows simulated outputs when the neural network model if feed with

training data. In this figure we can distinguish two lines, the first one is a red dot line

referred to the output when PRS inputs signal were applied to the SIMULINK plant

model; the continues blue line refers to the simulated output of the network.

Same as above Figure 7 shows simulated outputs when validating data were

applied to the network.

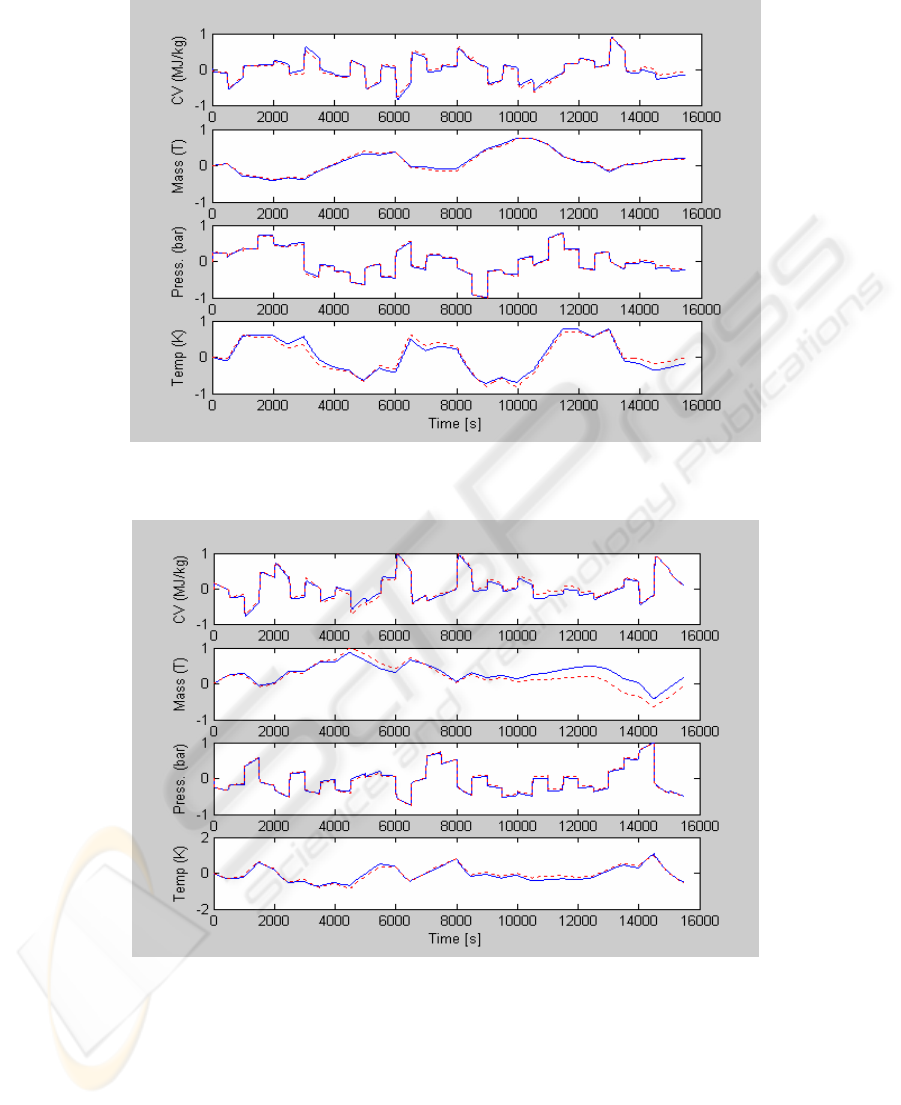
Fig. 6. Simulated output for training data.

Fig. 7. Simulated output for validating data.

100

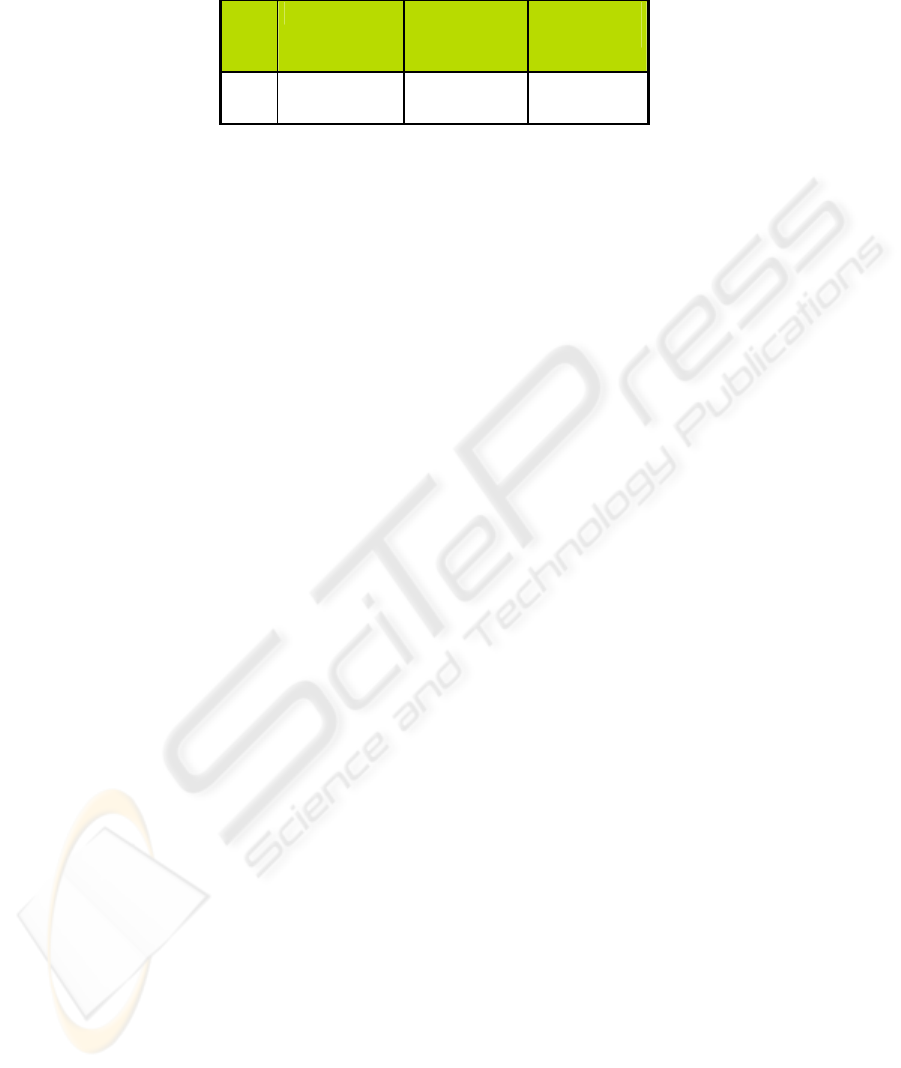
Table 2. Mean Square Error

Table 2 shows the Mean Square Error (MSE) for: the training process, the

simulation with the information of training and the simulation with other information

for validation. MSE are low for the simulation of neuronal network with the same

data using in the training, while using other data, column of validation, the MSE is

greater. This is because when simulating using training data set we do not use delayed

output as input to the network; and when simulating using validating data, this set of

data is completely new for the network so it tries to follow what it have learned from

the training process.

3 Conclusions

The present paper consists on a first study of the Gasifiers Modeling by empirical

methods, specifically the based on Neural Networks:

− The theoretical study of the gasification has allowed us to know the principles of

this complex process.

From the system’s point of view, we conclude that the Gasifier plants are a

platform for the development of the methodologies of advanced control.

− The theoretical study on neural networks has allowed us to familiarize with this

technology so useful and applicable to so diverse problems. In specific, the

application of this technology to the empirical modeling of dynamical systems can

be very much suitable in case of systems with highly non linearity.

− The simulated ALSTOM Gasifier offers us an important tool for the application of

methodologies of modeling, allowing us to extract conclusions before the

application to the real system.

− For the case of variations of maximum 10 % in the inputs, was not found

difficulties in training the net. It is important that information would be

representative of the behavior of the system in the whole operation range.

− With the employment of Neural Network to the simulator, the familiarization has

been obtained as much by the Neural Network Toolbox of Matlab, as by the

methodology of application of static networks for a dynamical process type black

box, defined by its inputs and outputs.

Training

simulation

Validating

simulation

MSE 9.4413e-005 0.0025456 0.069403

101

− Some architectures were proved and a network type perceptron with two layers, the

first one of sigmoid and linear the second one has been chosen as firstly attempt for

the application of the methodology.

References

1 Dixon R., A.W. Pike and M. S. Donne, “The ALSTOM benchmark challenge on gasifier

control”. Proc. Instn. Mech. Eng., Part I, J of Syst and Cont Eng, 214, (16), 2000, pp 389-

394.

2 Special Issue on the ALSTOM Gasifier Control Benchmark Challenge, Proc. Instn. Mech.

Eng., Part I Journal of Systems and Control Engineering, 214, (16), 2000.

3 Dixon,R., 2002, “Alstom Benchmark Challenge II: Control of a Non-Linear Gasifier

Model”, ALSTOM, available from

http://www.iee.org/OnComms/PN/controlauto/Specification_v2.pdf

4 Dixon R., A.W. Pike (2004), Introduction to the 2nd Alstom BenchmarkChallenge on

Gasifier Control. University of Bath, ID-255 UK, Loughborough University, LE11 3TU,

UK.

5 Ljung, L (1987). “System identification”. Prentice Hall, Englewood cliffs, NJ.

6 Paulo Gil, Jorge Henriques, António Dourado, H. Duarte-Ramos “Non-Linear predictive

control based on a recurrent neural network”, Portugal – Disponible en CiteSeer, Scientific

Literature Digital Lybrary, http://citeseer.ist.psu.edu/388047.html

7 Sjoberg J., Zhang Q., Ljung L., Benveniste A., Delyon B., Glorennec P.-Y., Hjalmarsson

H., Juditsky A. (1995,December), "Nonlinear black-box modeling in system identification:

a unified overview," Automatica, Vol.31, No.12, pp.1691-1724.

8 Howard Demuth, Mark Beale, “Neural Network Toolbox User’s Guide Version 3.0”,

Neural Network Toolbox 4.0.1, http://www.mathworks.com

102