
SOLVING AN INVERSE KINEMATICS PROBLEM FOR A
HUMANOID ROBOT’S IMITATION OF HUMAN MOTIONS USING
OPTIMIZATION
ChangHwan Kim, Doik Kim and Yonghwan Oh
Intelligent Robotics Research Center
Korea Institute of Science and Technology
P.O. Box 131, Cheongryang, Seoul 130-650, Korea
Keywords:
Human Motion Imitation, Inverse Kinematics Problem, Motion Capture System, Optimization.
Abstract:
Interactions of a humanoid with a human are important, when the humanoid is requested to provide people
with human-friendly services in unknown or uncertain environment. Such interactions may require more com-
plicated and human-like behaviors from the humanoid. In this work the arm motion of a human is discussed
as the early stage of human motion imitation by a humanoid. A motion capture system is used to obtain
human-friendly arm motions as references for the humanoid. However the captured motions may not be ap-
plied directly to the humanoid, since the differences in geometric or dynamics aspects as length, degrees of
freedom, and kinematics and dynamics capabilities exist between the humanoid and the human. To overcome
this difficulty a method to adapt captured motions to a humanoid is developed. The geometric difference in
the arm length is resolved by scaling the arm length of the humanoid with a constant based on a length ra-
tio. Using the scaled geometry of the humanoid the imitation of actor’s arm motion is realized by solving an
inverse kinematics problem that is formulated as an optimization problem. The errors between the captured
trajectories of actor arms and the approximated trajectories of humanoid arms are minimized. Such dynamics
capabilities of the joint motors as limits of joint position, velocity and acceleration are also imposed on the
optimization problem. Two motions of one hand waving and performing a statement in sign language are
imitated by a humanoid in dynamics simulation.
1 INTRODUCTION
Interactions between a human and a robot, especially
a humanoid, will have been being more important for
the robot to work with the human in unknown or un-
certain environment. Such interactions may require
more complicated and human-like motions from a hu-
manoid such that the motions are safe and friendly to
humans. The humanoid can be controlled by planning
motions or may be taught by humans to perform com-
plex motions for working with humans. For the sec-
ond case the humanoid may learn certain motions di-
rectly from a human through its cameras and other de-
vices. In other words the humanoid will be required to
move more intelligently if it lives with humans daily
in the future. From this reason the humanoid needs to
imitate human motions.
The process of human motion imitation begins with
measuring human motions as accurately as possible.
The most popular way for the measurement is to use
a motion capture system that can capture the motions
of a human in the form of time trajectories of mark-
ers attached on the human body. These human mo-
tions have been used for animation or human motion
analysis. However those captured motions may not
be applicable directly to the humanoid, since the dif-
ferences between the two characters, human and hu-
manoid, in the geometric and system aspects exist.
On the other hands, the lengths, masses, and move-
ment capabilities of the humanoid are much differ-
ent from those of the human such that the appropriate
conversion of the captured motions to the humanoid
is needed.
The imitation of a human motion by a humanoid
has been studied by some researchers. (Dasgupta and
Nakamura, 1999) presented an adaptation method of
human motion capture data to obtain a feasible walk-
ing pattern for a humanoid. The developed method
used a Fourier expansion to determine desired trajec-
tories of the Zero Moment Point (ZMP) from human
motion capture database. An optimization problem
to compute the reaction forces of the foot against the
ground corresponding to the desired ZMP trajectories,
was formulated. Arm motions were not however dis-
85
Kim C., Kim D. and Oh Y. (2005).
SOLVING AN INVERSE KINEMATICS PROBLEM FOR A HUMANOID ROBOT’S IMITATION OF HUMAN MOTIONS USING OPTIMIZATION.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 85-92
DOI: 10.5220/0001180100850092
Copyright
c
SciTePress

cussed in this work.
(Nakaoka et al., 2003) explored a procedure to let
a humanoid (HRP-1S) imitate a Japanese folk dance
captured by a motion capture system. Symbolic rep-
resentations for primitive motions that consisted of
essential arms’ postures and legs’ steps, were pre-
sented. The time trajectories of joint positions were
first generated to imitate the primitive motions. These
trajectories were then modified satisfying mechanical
constraints of the humanoid. Especially, for the dy-
namic stabilities the trajectory of waist was modified
to be consistent with the desired ZMP trajectory. The
imitation of the Japanese folk dance was performed
in OpenHRP dynamics simulator and was realized by
the real humanoid of HRP-1S as well. As the exten-
sion of this work, (Nakaoka et al., 2004) updated the
forgoing developed method. The updated method fo-
cused more on leg motions using a symbolic descrip-
tion of leg motion primitives in the same Japanese
folk dance. By solving a inverse kinematics problem
for the upper body of a human the arm motions of
the humanoid were determined. The joint positions
obtained from that inverse kinematics problem were
then modified by the velocity limits of joint motors.
The leg motions were also obtained from the inverse
kinematics problem and were modified according to
the desired ZMP trajectories. The entire dance was
performed at the half of the speed of the original cap-
tured dance to avoid falling down.
(Pollard et al., 2002) also developed a method to
adapt captured human motions to a humanoid that
consists of only a upper body. The captured upper
body motions of an actor was optimized, minimiz-
ing the posture differences between the humanoid and
the actor. The limits of joint position and velocity of
the humanoid were also involved. However, in these
studies the description of the conversion of the mo-
tion capture data to the humanoid was not made in
that detail.
(Zhao et al., 2004) presented a kinematics mapping
of captured human motion data to a humanoid intro-
ducing a similarity function. The similarity function
was defined using the errors between the joint posi-
tions of an actor and those of a humanoid. The num-
ber of degrees of freedom (DOF) of the humanoid was
assumed to be same as that of the human, which may
not be very realistic.
In the studies mentioned so far the procedure to
obtain the trajectories of joint position and velocity
of a humanoid from human motion capture data has
been explored insufficiently. In other words, it was
not clearly described to transform motions of a hu-
man having more DOF to the humanoid having less
DOF. Therefore this work will discuss more details
about that conversion process.
It is one of the key tasks for a humanoid to imitate
human arm motions, since such tasks are essential in
providing people with human-friendly behaviors. It is
also difficult to imitate the arm motions due to com-
plexity and delicateness of the motions. In addition,
incorrect imitation of arm and hand motions may lead
misunderstandings to people about the original mean-
ing. The imitation of human arm motions will be dis-
cussed as the start of human motion imitation.
As mentioned earlier it is difficult to apply captured
human arm motions to a humanoid because of several
differences between a human and a humanoid as fol-
lowed
• arm length difference
• length rate difference of upper and lower arms
• less degrees of freedom of a humanoid than those
of a human
• dynamics capability difference
To resolve the difficulty due to the differences
above an efficient method using optimization for con-
verting captured human arm motions to a humanoid
will be discussed. In addition, a simple way to im-
pose limits of joint position and velocity will be pro-
posed. Two human arm motions will be imitated by
the humanoid in dynamics simulation to evaluate the
developed method.
2 GEOMETRIC SCALING OF
HUMANOID ARMS
One of the difficulties of adapting human motions to
a humanoid robot is to have the work space of hu-
manoid arms be similar to that of human arms. To re-
solve this difficulty (Hodgins and Pollard, 1997) pro-
posed a rule for geometric and mass scaling to adapt
existing simulated behaviors of a character to new
characters. In the proposed rule the geometric scal-
ing for running motion of a human was done using a
scaling factor based on the height and the leg length of
a new character. For other motions a different scaling
factor was selected for more reliable animation.
In this work a scaling rule similar to (Hodgins and
Pollard, 1997) is used. In detail the arm length of
the humanoid robot is scaled by multiplying a dimen-
sionless constant, ρ = (
L
human
L
robot
) to it. L
human
de-
notes the sum of the lengths of the upper and lower
arm of an actor as seen in Fig.1. L
robot
is also de-
fined for the humanoid in the same manner. Therefore
the lengths of the upper and lower arms of humanoid
are scaled as ρL
upper
robot
and ρL
lower
robot
. The same scaling
rule is applied to the left or right arm using different
scaling constants, respectively. The boundary of the
work space of the arms may then become similar to
the actor’s. However, the scaled work space may not
be identical to that of the actor due to the differences
ICINCO 2005 - ROBOTICS AND AUTOMATION
86

Figure 1: The upper body of a human in capturing (left) and
a humanoid having 27 degrees of freedom (right).
in the length ratios of the arms. Due to this when the
position and orientation of humanoid hands are imi-
tated, the orientation of the upper arm is also forced
to match with human’s at the same time. Based on
the scaled geometry of the humanoid the actor’s arm
motions are imitated by solving an inverse kinematics
problem in the following section.
3 OPTIMIZATION
FORMULATION FOR INVERSE
KINEMATICS
Human motions can be recorded and stored using a
motion capture system. It can be formulated as an in-
verse kinematics problem for a humanoid to perform
these captured motions. In the following subsections
it will be shown that this inverse kinematics problem
can be formulated as an optimization problem consid-
ering motor capabilities.
3.1 Minimization of Errors in Arm
and Hand Postures
The trajectories of humanoid arms can be determined
using the captured position and orientation trajecto-
ries of actor’s hands and upper arms as some re-
searchers like (Lenarcic and Ravani, 1994) had done.
The method presented in (Lenarcic and Ravani, 1994)
is possible to solve the inverse kinematics problem
discussed herein, since the humanoid has 6DOF for
an arm and a hand. The method can solve the
inverse kinematics problem using a generalized in-
verse matrix of the Jacobian of an end-effector (hand
of the humanoid) and joint velocity limits. It may
however be difficult to impose such more general
constraints as dynamic stabilities and avoiding self-
collision on those methods. Furthermore, although
the position and orientation of the humanoid is suc-
cessfully imitated, the arm motion of the humanoid
may be matched incorrectly with that of the actor
due to the difference in degrees of freedom. In other
words, more accurate imitation of the hand motions
may cause more errors in the motion of the upper arm,
since the humanoid has less degrees of freedom, espe-
cially at the wrist, than the actor. Due to this reason a
more general method is needed to minimize the errors
in the trajectories of hand and upper arm simultane-
ously. This can be accomplished using optimization
with weights on hand and upper arm motions sepa-
rately. Additionally, use of optimization allows to im-
pose more general constraints as motor capacities.
An optimization problem is formulated now to de-
termine the optimal postures of the humanoid arms
imitating the actor’s arm motions captured by the mo-
tion capture system. The same optimization problem
is solved repeatedly at each of the time grid points in
the entire motion interval. Once the optimal posture
is obtained at a certain time grid point, this posture is
used as the initial value for the optimization problem
for the next time grid point. Therefore, the increment
of configuration of the humanoid is defined as the op-
timization variable as follows
∆q
j
i
= q
j
i
− q
j
i−1
for j = 1 ∼ 6 (1)
where q
j
i
is the j
th
joint in the arm at the i
th
time
grid point. Notice that the joint numbers j = 1 ∼ 6
are given from the shoulder to the hand for the both
arms as seen in Fig.1. It is also noticed that the op-
timization formulation defined here can be applied to
the both arms. Therefore the solution procedure will
be explored for the right arm through the entire paper
but it can be simply repeated to the left one as well.
Six markers were used when the motion of each
arm of the actor was captured; three markers were at-
tached on the hand (wrist, thumb, pinky), one marker
at the elbow, one on the bicep, and the last one on
the shoulder. First, the error between the actor hand
and the humanoid hand is considered. That error is
defined in terms of the distances between the three
markers on the actor hand and the corresponding three
points on the humanoid hand approximated from the
given configuration. Secondly, the orientation error
between the upper arms of the actor and the humanoid
is involved. Therefore, at the i
th
time grid point,
t = t
i
, the error function to be minimized is given
as
min
∆θ
i
f(∆θ
i
) = E
hand
(∆θ
i
)
T
W E
hand
(∆θ
i
)
+ W
10
ks
elbow
(∆θ
i
)k
2
(2)
SOLVING AN INVERSE KINEMATICS PROBLEM FOR A HUMANOID ROBOT’S IMITATION OF HUMAN
MOTIONS USING OPTIMIZATION
87

where
E
hand
(∆θ
i
) =
r
ac
wrist
(t
i
) − r
hr
wrist
(∆θ
i
)
r
ac
thumb
(t
i
) − r
hr
thumb
(∆θ
i
)
r
ac
pinky
(t
i
) − r
hr
pinky
(∆θ
i
)
W = diag [ W
1
W
2
. . . W
9
]
∆θ
i
= [ ∆q
1
i
. . . ∆q
6
i
]
T
(3)
and W
10
is a weight for the second term in Eq. (2).
r
ac
wrist
(t
i
), r
ac
thumb
(t
i
) and r
ac
pinky
(t
i
) are the captured
trajectories of the position vectors of three markers
on the wrist, thumb and pinky of the actor hand,
respectively. Similarly, three points, r
hr
wrist
(∆θ
i
),
r
hr
thumb
(∆θ
i
), and r
hr
pinky
(∆θ
i
) are defined on the hu-
manoid hand in terms of the increments of joint posi-
tions and correspond to the three points on the actor
hand.
ks
elbow
k in (2) denotes the magnitude of the vec-
tor representing the orientation difference between the
upper arm of the actor and that of the humanoid as
seen in Fig.2. Its square is written in terms of ∆θ
i
as
ks
elbow
(∆θ
i
)k
2
=
(
r
ac
el/sh
(t
i
)
T
kr
ac
el/sh
(t
i
)k
r
hr
el/sh
(∆θ
i
)
)
2
− r
hr
el/sh
(∆θ
i
)
T
r
hr
el/sh
(∆θ
i
)
(4)
where
r
ac
el/sh
(t
i
) = r
ac
el
(t
i
) − r
ac
sh
(t
i
) (5)
r
hr
el/sh
(∆θ
i
) = r
hr
el
(∆θ
i
) − r
hr
sh
(∆θ
i
) (6)
where r
ac
el
(t
i
) and r
ac
sh
(t
i
) are the position vectors of
the elbow and the shoulder of the actor at the time
grid point, t
i
, which are determined from the capture
marker data. r
hr
el
(∆θ
i
) and r
hr
sh
(∆θ
i
) are the approx-
imated position vectors of the elbow and the shoulder
of the humanoid in the configuration, ∆θ
i
, at the time
grid point, t
i
.
As seen in Fig.2 the position and orientation of the
humanoid hand are matched with those of the actor
hand by minimizing the first term in the objective
function in (2), since a plane can be defined by three
points. This method has advantages of reducing com-
putation efforts, since it does not need to compute the
orientation angles of the hand from its rotational ma-
trix.
Minimizing the error in the position and orienta-
tion for the hand may not be enough to imitate the
entire arm motions of the actor, since the humanoid
has less degrees of freedom for the arm than the ac-
tor does. Due to this the orientation error between the
upper arm of the humanoid and the actor is reduced
Figure 2: Marker positions on the hands of actor and hu-
manoid, and the vector s
elbow
.
by minimizing the second term in Eq.(2). Therefore
the proposed method does not calculate the Euler an-
gles for the configuration from the rotational matrices
given in the captured motions. This advantage allows
to obtain analytical gradients of the objective function
and reduce computations for the iterative optimization
process.
3.2 Kinematic Constraints of Motor
Capabilities
The imitation of the arm motions can be limited by
several kinematic constraints as motor capabilities.
The motor capabilities consist of the angle limit, ve-
locity, and acceleration. The angle limits of the joints
are imposed with easy as
q
lower
j
≤ q
j
i
≤ q
upper
j
for j = 1 ∼ 6 (7)
where q
lower
j
and q
upper
j
for j = 1 ∼ 6 are the posi-
tion limits of the joints for the arm, and q
j
i
= q
j
(t
i
)
as in (1).
Recalling Eq.(1), the joint positions at the time, t
i
,
can be given in a discrete form as
q
j
i
= q
j
i−1
+ ∆q
j
i
for j = 1 ∼ 6 (8)
where the joint positions, q
j
i−1
for j = 1 ∼ 6 are
known from the previous time grid point, t
i−1
. The
inequalities in Eq.(7) are then rewritten in terms of the
incremental limits of the joint positions using Eq.(8)
as
∆q
lower
j
≤ ∆q
j
i
≤ ∆q
upper
j
for j = 1 ∼ 6 (9)
where
∆q
lower
j
= q
lower
j
− q
j
i−1
∆q
upper
j
= q
upper
j
− q
j
i−1
.
(10)
ICINCO 2005 - ROBOTICS AND AUTOMATION
88
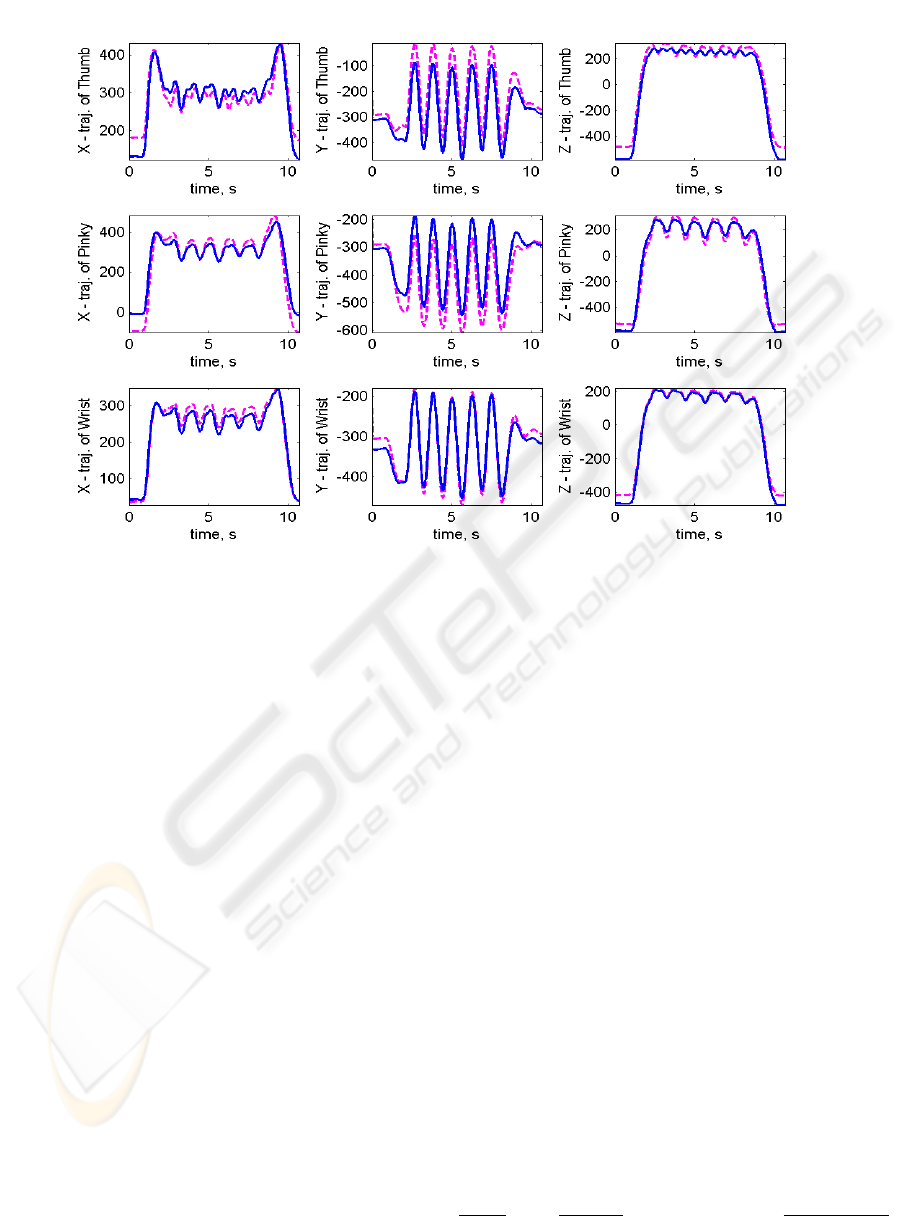
Figure 3: The marker trajectories of the actor’s right hand (solid lines; mm unit) and the optimal trajectories of corresponding
points on the humanoid hand (dash lines) for the motion of waving the right hand.
The capacities of motors at the joints are also lim-
ited by the bounds of motor angular velocities and ac-
celerations as follows
˙q
lower
j
≤ ˙q
j
i
≤ ˙q
upper
j
for j = 1 ∼ 6 (11)
¨q
lower
j
≤ ¨q
j
i
≤ ¨q
upper
j
for j = 1 ∼ 6 (12)
where ˙q
lower
j
, ¨q
lower
j
, ˙q
upper
j
, and ¨q
upper
j
for j = 1 ∼
6 are the lower and upper bounds of the joint veloci-
ties and accelerations, respectively. The joint veloci-
ties and accelerations at t
i
can be written in a discrete
form using the Backward Difference Method (BDM).
Using the BDM the inequalities in Eqs.(11) and (12)
can be rearranged in terms of the increments of joint
position at t = t
i
as
∆ ˙q
lower
j
≤ ∆q
j
i
≤ ∆ ˙q
upper
j
for j = 1 ∼ 6 (13)
Ƭq
lower
j
≤ ∆q
j
i
≤ ∆¨q
upper
j
for j = 1 ∼ 6 (14)
where
∆ ˙q
lower
j
= ∆t ˙q
lower
j
∆ ˙q
upper
j
= ∆t ˙q
upper
j
Ƭq
lower
j
= ∆t ˙q
j
(t
i−1
) + ∆t
2
¨q
lower
j
Ƭq
upper
j
= ∆t ˙q
j
(t
i−1
) + ∆t
2
¨q
upper
j
.
(15)
In the equations above ˙q
j
(t
i−1
) can be determined us-
ing the BDM.
The imitation of the arm motion is done by mini-
mizing the objective function in Eq.(2) subject to sets
of bounds for the joint increments in Eqs.(9), (13) and
(14). This optimization problem is solved using SQP
algorithm for nonlinear programming.
3.3 Gradients
In this work a gradient-based optimization scheme is
used so that the analytical gradients of the objective
and constraint functions are recommended to reduce
optimization iterations. All the constraints in Eqs.(9),
(13) and (14) are the bounds on the optimization vari-
ables, ∆q
j
i
for j = 1 ∼ 6 such that their gradients are
simply obtained. The gradient of the objective func-
tion in (2) is given as
∂f
∂∆θ
i
= 2
∂E
hand
∂∆θ
i
T
W E
hand
+W
10
∂(ks
elbow
k
2
)
∂∆θ
i
(16)
SOLVING AN INVERSE KINEMATICS PROBLEM FOR A HUMANOID ROBOT’S IMITATION OF HUMAN
MOTIONS USING OPTIMIZATION
89

where using Eqs.(3) and (4)
∂E
hand
∂∆θ
i
=
−
∂r
hr
wrist
∂∆θ
i
−
∂r
hr
thumb
∂∆θ
i
−
∂r
hr
pinky
∂∆θ
i
=
−
∂r
hr
wrist
∂θ
i
−
∂r
hr
thumb
∂θ
i
−
∂r
hr
pinky
∂θ
i
.
(17)
Equations (1) and (3) were used herein, since ∆θ
i
=
θ
i
− θ
i−1
and θ
i−1
is known. In addition,
∂(ks
elbow
k
2
)
∂∆θ
i
= −
∂r
hr
el/sh
∂∆θ
i
T
r
hr
el/sh
+ 2
(
r
ac
el/sh
T
kr
ac
el/sh
k
2
r
hr
el/sh
)
∂r
hr
el/sh
∂∆θ
i
T
r
ac
el/sh
(18)
Equations (17) and (18) are determined easily, since
the Jacobians of the position vectors for those equa-
tions are given analytically.
As mentioned before, since all the error terms are
written in terms of the position vectors that are repre-
sented with the joint positions, the gradients above are
obtained analytically. Due to the same reason compu-
tation efforts may be reduced compared with obtain-
ing gradients numerically. The proposed method can
also deal with general constraints given in terms of
the position vectors such as self-collision avoidance.
4 EXAMPLES: WAVING AND
SIGN LANGUAGE
To evaluate the developed method a couple of mo-
tions of an actor were captured by the Hawk Digital
System commercially available from Motion Analy-
sis Inc.. 25 markers were attached on the upper body.
The motions of waving and performing a statement in
sign language were recorded at the rate of 60 Hz with
642 frames and 1978 frames, respectively.
For the motion of waving the captured trajecto-
ries of the three markers on the right hand of actor
and those of the corresponding three points on the
right hand of humanoid are plotted in Fig.3 showing
good agreements with each other. In some parts of
the motion for the thumb and pinky small errors be-
tween the humanoid and the actor was observed. That
may be due to the limits of joint positions and veloci-
ties of the humanoid. Therefore another procedure to
compensate the motion imitated insufficiently may be
needed. This is also another task for the future work.
The optimal joint positions obtained from the opti-
mization problem are shown in Fig.4. The figure also
shows that the joint positions are bounded by the time
varying limits obtained from the position and velocity
bounds of joint motors. These varying limits are ob-
tained from the set of bounds for the joint increments
in Eqs.(9) and (13) in Sec. 3.2. It is noticed that the
bounds by the acceleration limits in (14) are not con-
sidered in this work but it will have to be added in the
future work. The dynamics simulation for this motion
is given in Fig.5.
In Fig.6 a statement in sign language is imitated by
the humanoid. The statement means, ”I’d like to give
hope and pleasure to you, and I love all of you.”. The
motion imitated is well matched with one performed
by the actor.
Once the joint positions are obtained from the cap-
tured trajectories of the actor arms, the joint veloci-
ties are determined numerically. These joint positions
and velocities are then applied to the humanoid as de-
sired trajectories for controlling the humanoid with
PID controller. The converted two motions are sim-
ulated in the dynamics simulator developed by the
Korea Institute of Science and Technology as seen in
Figs.5 and 6 .
5 DISCUSSION
A method has been proposed to transform the motion
capture data of human arms to joint positions and ve-
locities available to a humanoid. The method was able
to overcome less degrees of freedom in the humanoid.
The proposed method employed a general optimiza-
tion scheme imposing limits on the capacities of the
joint motors such that it could provide a solution pro-
cedure for an inverse kinematics problem. Since the
error terms in the objective function were written in
terms of only the marker’s trajectories, less computa-
tion efforts were needed than obtaining Euler angles
of the arms from rotational matrices. Due to this it
may be useful to control a humanoid in real time. In
addition it is easy to impose general constraints as the
Zero Moment Point (ZMP) and self-collision avoid-
ance on the humanoid motions, because a general op-
timization scheme was used. Two captured motions
of waving and performing a statement in sign lan-
guage have been imitated by the humanoid, showing
good agreements with the captured motions through
dynamics simulation. The method will be extended
to whole body imitation considering dynamic balanc-
ing and self-collision avoidance in the near future.
ICINCO 2005 - ROBOTICS AND AUTOMATION
90
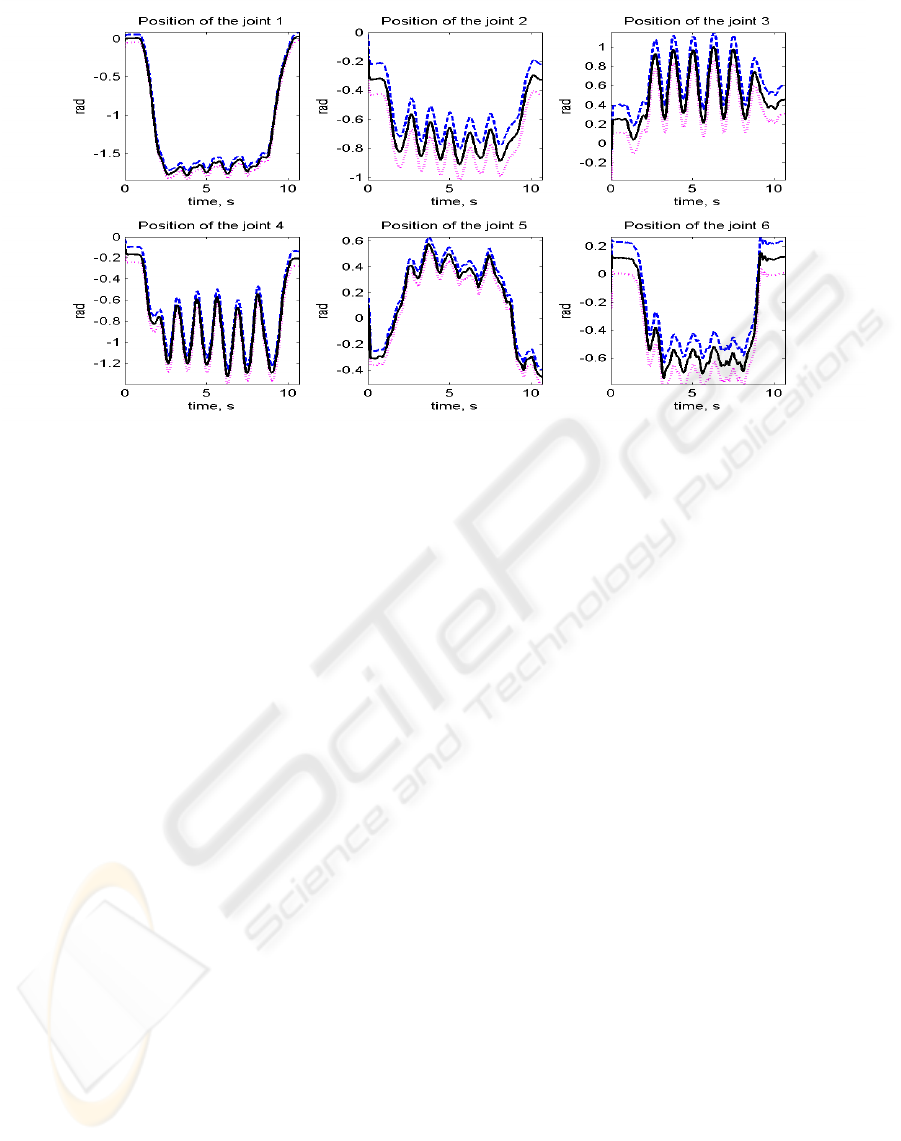
Figure 4: The optimal joint positions (solid lines) of the right arm for the motion of waving the right hand with upper (dash
lines) and lower (dot lines) limits: The joints 1, 2, and 3 are for the shoulder, the joint 4 for the elbow, and the joints 5 and 6
for the wrist and the hand, respectively.
REFERENCES
Dasgupta, A. and Nakamura, Y. (1999). Making feasible
walking of humanoid robots from human motion cap-
ture data. In International Conference on Robotics
and Automation, pages 1044–1049. Detroit, Michi-
gan.
Hodgins, J. K. and Pollard, N. S. (1997). Adapting simu-
lated behaviors for new charaters. In SIGGRAPH97
Proceedings. Los Angeles, CA.
Lenarcic, J. and Ravani, B. (1994). Advances In Robot
Kinematics And Computational Geometry. Kluwer
Academic Publishers, 101 Philip Drive, Norwell, MA
02061, U.S.A., 1st edition.
Nakaoka, S., Nakazawa, A., Yokoi, K., Hirukawa, H., and
Ikeuchi, K. (2003). Generating whole body motions
for a biped humanoid robot from captured human
dances. In International Conference on Robotics and
Automation, pages 3905–3910. Tapei, Taiwan.
Nakaoka, S., Nakazawa, A., Yokoi, K., and Ikeuchi, K.
(2004). Leg motion primitives for a dancing hu-
manoid robot. In International Conference on Robot-
ics and Automation, pages 610–615. New Orieans,
LA, U.S.A.
Pollard, N. S., Hodgins, J. K., Riley, M. J., and Atkeson,
C. G. (2002). Adapting human motion for the control
of a humanoid robot. In International Conference on
Robotics and Automation. Washington, DC, U.S.A.
Zhao, X., Huang, Q., Peng, Z., and Li, K. (2004). Kine-
matics mapping and similarity evaluation of humanoid
motion based on human motion capture. In Interna-
tional Conference on Intelligent RObots and Systems.
Sendai, Japan.
SOLVING AN INVERSE KINEMATICS PROBLEM FOR A HUMANOID ROBOT’S IMITATION OF HUMAN
MOTIONS USING OPTIMIZATION
91

Figure 5: Waving the right hand: the captured motion of the actor (the 1
st
row) and the motion imitated by the humanoid (the
2
nd
row).
Figure 6: Sign language motions: the captured motions of the actor (the 1
st
and 3
rd
row) and the motions imitated by the
humanoid (the 2
nd
and 4
th
row).
ICINCO 2005 - ROBOTICS AND AUTOMATION
92
