Variable Support Control for the Wave Equation

A Multiplier Approach

Antonio Agresti

, Daniele Andreucci

and Paola Loreti

Mathematics Department, Sapienza University, Piazzale Aldo Moro, 5, 00185, Rome, Italy

SBAI Department, Sapienza University, Via Antonio Scarpa, 16, 00161, Rome, Italy

Keywords:

Exact Controllability, Wave Equation, Variable Control Subset, Multiplier.

Abstract:

We study the controllability of the multidimensional wave equation in a bounded domain with Dirichlet boun-

dary condition, in which the support of the control is allowed to change over time.

The exact controllability is reduced to the proof of the observability inequality, which is proven by a multiplier

method. Besides our main results, we present some applications.

1 INTRODUCTION

The controllability of the wave equation or more ge-

nerally of partial differential equations has been stu-

died intensively in the last 30 years. Exact control-

lability for evolutive systems is a challenging mathe-

matical problem, also relevant in engineering applica-

tions. The exact controllability of the wave equation

with Dirichlet boundary condition using the multi-

plier method is studied in (Lions, 1988) see also (Ko-

mornik, 1994) for a systematic study of this method

and, for an approach using theory of semi-groups see

(Tucsnak and Weiss, 2009). All these results do not

allow the support of the control to change over time,

while this variability is required in some applications

(see (Dessi et al., 2004)-(Carcaterra et al., 2014)).

The numerical implementation of controllability

problems is widely studied in literature (see for is-

tance (Glowinski and Lions, 1995), (Castro et al.,

2008), (M

unch, 2005), (Zuazua, 2005) and the refe-

rences therein). In this works, the abstract procedure

used to show the controllability plays an important

role to prove the convergence of the scheme; see e.g.

(Castro et al., 2008). The present results provide the

abstract framework to the numerical implementation

in the variable support control case.

In this paper we provide a controllability result

which extends the classical controllability results and

admits variability of the control support over time.

We have to point out that even in the ﬁxed support

case, the subset of the boundary, on which the cont-

rol acts, cannot be chosen arbitrarily; for an extensive

discussion on these topics see (Bardos et al., 1992).

The common strategy to prove the exact control-

lability is to study an equivalent property i.e. the ex-

act observability for the adjoint system (for more on

this see (Komornik and Loreti, 2005), (Tucsnak and

Weiss, 2009)). Our approach is based on the multi-

plier method (see (Komornik, 1994), (Lions, 1988)),

which seems the most powerful in the multidimen-

sional case. Although the strategy of the proof is

quite classical and follows essentially (Lions, 1988),

this approach leads to some unexpected results and it

opens some questions on the optimality of these re-

sults; see (Agresti et al., 2017) for more on this.

Here we dwell more on the multidimensional case

which seems to be closer to applications, providing

some explicit examples in special geometries.

Let us begin with some notations:

• Let Ω be a bounded domain of R

with d ≥ 1,

of class C

or convex. From the hypothesis on the

boundary, we know that the exterior normal vector

ν is well deﬁned H

d−1

-a.e. on ∂Ω; where H

d−1

is the d −1 dimensional Hausdorff measure (see

(Evans and Gariepy, 2015)). Moreover, we denote

dΓ the measure H

d−1

restricted to ∂Ω.

• For each t ∈ (0,T ) and T > 0, Γ(t) denotes an

open subset of ∂Ω.

• Finally, we deﬁne

Σ :=

[

t∈(0,T )

Γ(t) ×{t}; (1.1)

and we suppose it to be H

d−1

⊗L

-measurable

(as deﬁned in (Evans and Gariepy, 2015) Chapter

1).

Agresti, A., Andreucci, D. and Loreti, P.

Variable Support Control for the Wave Equation - A Multiplier Approach.

DOI: 10.5220/0006832600330042

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 33-42

ISBN: 978-989-758-321-6

In this paper we want to study the following property.

Deﬁnition 1.1 (Exact Controllability). We say that

the system











−∆w = 0 , (x,t) ∈ Ω ×(0,T ) ,

w = 0 , (x,t) ∈ ∂Ω ×(0,T ) \Σ,

w = v , (x,t) ∈ Σ ,

w = w

, (x,t) ∈ Ω ×{0},

= w

, (x,t) ∈ Ω ×{0};

(1.2)

is exactly controllable in time T > 0, if for all

∈ L

(Ω) and w

∈ H

−1

(Ω) there exists a

control v ∈ L

(Σ) such that the unique solution w ∈

C([0, T ]; L

(Ω)) ∩C

([0,T ]; H

−1

(Ω)) of (1.2) satis-

ﬁes

w(x,T ) = z

, w

(x,T ) = z

. (1.3)

Of course, the problem (1.2) has to be intended in

a weak sense, which we give below (see Deﬁnition

1.3).

In the following, it will be useful to know some

properties of the solution of the wave equation with

null Dirichlet boundary condition, i.e.











−∆u = 0 , (x,t) ∈ Ω ×R

u = 0 , (x,t) ∈ ∂Ω ×R

u = u

, (x,t) ∈ Ω ×{0},

= u

, (x,t) ∈ Ω ×{0};

(1.4)

where R

:= [0,∞). In particular, we will need the

following proposition; see (Pazy, 2012) for the notion

of classical and mild solution.

Proposition 1.2. The following holds true:

i) For each (u

) ∈ H

(Ω) ×L

(Ω), then the pro-

blem (1.4) has an unique mild solution u in the

class

(Ω)) ∩C(R

(Ω)).

ii) For each (u

) ∈ (H

(Ω) ∩H

(Ω)) ×H

(Ω),

then the problem (1.4) has an unique classical so-

lution u in the class

C(R

(Ω) ∩H

(Ω)) ∩C

(Ω)).

Proof. Let {f

: k ∈N} and {λ

: k ∈N} be respecti-

vely the eigenfunctions and the eigenvalues of the

Laplace operator with null Dirichlet boundary condi-

tion.

Since Ω is of class C

or convex, then f

∈ H

(Ω) ∩

(Ω) for all k ∈ N; for a proof see (Taylor, 2011) or

(Grisvard, 2011). Then, the solution u of the problem

(1.4) is

u(t) =

∞

∑

k=0



cos(λ

t) ˆu

0,k

sin(λ

ˆu

1,k



; (1.5)

where

ˆu

i.k

:= (u

, f

)

(Ω)

Ω

dx , i = 0, 1 .

Then the representation of the solution in (1.5) readily

implies the claim in i) −ii).

With this in hand, we can give a deﬁnition of so-

lution for the problem (1.2).

Deﬁnition 1.3 (Weak Solution of (1.2)). A map w ∈

C([0, T ]; L

(Ω)) ∩C

([0,T ]; H

−1

(Ω)) is a weak solu-

tion of (1.2) with v ∈ L

(Σ) and (w

) ∈ L

(Ω) ×

−1

(Ω) if and only if

−hw

(s),u(s)i

−1

×H

+ hw(s),u

(s)i

×L

−hw

−1

×H

+ hw

×L

Γ(t)

v∂

u dΓdt , (1.6)

for all 0 < s ≤ T and for all mild solutions u of (1.4)

and initial data (u

) ∈ H

(Ω) ×L

(Ω).

For the motivation see (Komornik and Loreti,

2005); for other equivalent formulations one may

consult (Lions, 1988).

Remark 1.4. Note that, on the RHS of (1.6) it appears

∂

u i.e. the normal derivative of u. Although the re-

gularity of a mild solution u is not sufﬁcient to have a

well deﬁned trace for ∂

u, in the sense of Sobolev spa-

ces (see (Taylor, 2011) Chapter 4), the normal deriva-

tive ∂

u is a well deﬁned element of L

(∂Ω ×(0,t))

for each t > 0: this result is generally called hidden

regularity; the proof relies on a clever integration by

parts argument, for details see (Komornik, 1994), (Li-

ons, 1988) or (Lasiecka and Triggiani, 1983). By this,

the last term in the RHS of (1.6) is well deﬁned since

v ∈ L

(Σ).

Before proceeding in the analysis of the weak so-

lutions, we recall the following well known result

about the solutions of the wave equation (1.4).

Corollary 1.5 (Energy conservation). For each t ∈

and each mild solution u of (1.4) with initial data

) ∈ H

(Ω) ×L

(Ω), the energy

E(t) =



k∇u(·,t)k

(Ω)

+ ku

(·,t)k

(Ω)



, (1.7)

is constant, and it is equal to the initial energy



k ∇u

(Ω)

+ k u

(Ω)



. (1.8)

We conclude the treatment of the weak solution

with the following well posedness result, for a proof

see (Komornik and Loreti, 2005).

Theorem 1.6 (Well Posedness). For each (w

) ∈

(Ω) ×H

−1

(Ω) and v ∈L

(Σ), there exist a unique

weak solution of (1.2) in the sense of Deﬁnition 1.3.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

For brevity, as we said above, here we conﬁne our-

selves to the study of the following equivalent pro-

perty.

Deﬁnition 1.7 (Exact Observability). Let u ∈

C(R

(Ω)) ∩C

(Ω)) be the unique mild

solution of (1.4) for the initial data (u

) ∈

(Ω)×L

(Ω). Then the system is called exactly ob-

servable in time T > 0 if there exists a constant C > 0

such that

|∂

dΓ ⊗dt =

Γ(t)

|∂

dΓ dt ≥



k ∇u

(Ω)

+ k u

(Ω)



, (1.9)

for all (u

) ∈ H

(Ω) ×L

(Ω).

We remind that ∂

u is a well deﬁned L

(∂Ω ×

(0,T )) element (see Remark 1.4).

We are now in a position to prove an identity, which

is the basic tool in proving the exact observability for

some Σ’s.

Lemma 1.8 (A multiplier identity). Let u ∈

C(R

(Ω)) ∩C

(Ω)) be the mild solu-

tion corresponding to initial data (u

) ∈ H

(Ω) ×

(Ω). Then for each 0 ≤ s < τ and ξ ∈ R

, we have

∂Ω

(x −ξ) ·ν |∂

dΓ(x) dt =



Ω



∇u ·(x −ξ) +

d −1





+ (τ −s)E

;

(1.10)

where E

is the initial energy of the system as deﬁned

in (1.8) and [ f (t)]

:= f (s

) − f (s

Proof. For reader’s convenience, we divide the proof

into three steps.

Step 1. We ﬁrst suppose that u

are smoother, i.e.

∈ H

(Ω) ∩H

(Ω) and u

∈ H

(Ω). By Proposi-

tion 1.2, the solution to (1.4) is a classical solution, in

particular the quantities u

, for 1 ≤k, j ≤d, belong

to C(R

(Ω)); this will be used in the proof.

Under this assumption, the wave equation is solved by

u almost everywhere on Ω×R

, then we can multiply

the wave equation by (x −ξ) ·∇u and on integrating

over Ω ×(s,t), we obtain

Ω

((x −ξ) ·∇u)u

dx dt

−

Ω

((x −ξ) ·∇u)∆u dx dt = 0 . (1.11)

For the ﬁrst term on the LHS in (1.11), with a simple

integration by parts argument, we obtain

Ω

(x −ξ) ·∇u u



Ω

(x −ξ) ·∇u u



−

Ω

(x −ξ) ·

∇((u

)

)dx dt



Ω

(x −ξ) ·∇u u



Ω

)

dx dt ;

where, in the last inequality, we have used the Green’s

formulas, u

= 0 on ∂Ω ×(s,τ) and ∇ ·(x −ξ) = d.

For the second term in (1.11) we use a similar argu-

ment. Indeed, by Green’s formulas

Ω

((x −ξ) ·∇u) ·∆u dx dt

∂Ω

∂

u(x −ξ) ·∇u dΓdt

−

Ω

∇((x −ξ) ·∇u) ·∇u dx dt .

Now, using that ((u

)

= 2u

and ∇(x

−

)

= δ

k, j

for all 1 ≤ k, j ≤ d (here δ

k, j

is the Kro-

necker’s delta), one obtains

∇((x −ξ) ·∇u) ·∇u = |∇u|

(x −ξ) ·∇(|∇u|

);

pointwise. With simple computations, we have

Ω

((x −ξ) ·∇u) ·∆u dx dt =

∂Ω

(x −ξ) ·ν|∂

d −2

Ω

|∇u|

dx dt .

Putting all together and using that E(t) ≡ E

(cfr.

Corollary 1.5), we obtain

∂Ω

(x −ξ) ·ν|∂



Ω

(x −ξ) ·∇u u



+ (t −τ)E

d −1

Ω

−|∇u|

dx dt .

(1.12)

Step 2. In this step we rewrite the last term on LHS

in (1.12). Indeed, under the assumption of Step 1, the

wave equation is solved by u a.e. on Ω ×(s,τ), so

that on multiplying it by u, integration over Ω ×(s, τ)

and using Green’s formulas (recall that u = 0 on ∂Ω×

(s,τ))

0 =

Ω

u(u

−∆u)dx dt



Ω



−

Ω

−|∇u|

dx dt . (1.13)

Variable Support Control for the Wave Equation - A Multiplier Approach

Step 3. Combining the equalities (1.12)-(1.13) we

obtain (1.10) for classical solutions.

In the general case, choose sequences such that {u

0,k

k ∈ N} ⊂ H

(Ω) ∩ H

(Ω) and {u

1,k

: k ∈ N} ⊂

(Ω), such that

0,k

→ u

in H

(Ω), u

1,k

→ u

in L

(Ω).

Then passing to the limit in the identity (1.10) va-

lid for the solution u

for initial data (u

0,k

1,k

), one

obtain the claim.

Remark 1.9. The proof of Corollary 3.1 is based on

the multiplication of the wave equation against the

function m(x)·∇u = (x −ξ) ·∇u, which is called mul-

tiplier, which justiﬁes the name of the identity.

2 ALTERNATING OBSERVATION

For alternating observation we mean that there exists

a partition 0 =: t

−1

< t

< ··· < t

N−1

< t

=: T

of the interval [0,T ] such that

Γ(t) ≡ Γ

, ∀t ∈ (t

j−1

) j = 0 ..., N ; (2.1)

where Γ

⊂ ∂Ω is a ﬁxed subset for each j = 0 ... ,N.

Under the previous hypothesis, by (1.1) we have

Σ =

[

j=0

×(t

j−1

), (2.2)

up to a set of measure 0.

As pointed out in Section 1 the family {Γ

}

i=0,...,N

cannot be chosen arbitrarly; we construct this family

in a special form (see (2.5) below).

To do this, let {x

}

i=0,...,N

be an arbitrary family of

points in R

;

• For each i = 0,. .., N, deﬁne

= max{|x −x

||x ∈ Ω}, (2.3)

and for each i = 0, .. .,N −1, deﬁne

i+1,i

= |x

i+1

−x

|. (2.4)

• For each i = 0,. .., N, deﬁne

= {x ∈ ∂Ω |(x −x

) ·ν > 0}. (2.5)

Theorem 2.1 (Alternating Observability). In the pre-

vious notations, for each real number T such that

T > R

N−1

∑

i=0

i+1,i

+ R

, (2.6)

the system is exactly observable in time T , in the sense

of Deﬁnition 1.7 for Σ as in (2.2).

Proof. For each i = 0,. .., N, use the identity (1.10)

for ξ = x

, s = t

i−1

and τ = t

. On summing over i =

0,.. ., N such identities, we have

∑

i=0

i−1

(x −x

) ·ν |∂

dΓ(x) dt =

∑

i=0



Ω



∇u ·(x −x

) +

d −1

udx



i−1

+ T E

, (2.7)

since

∑

i=0

−t

i−1

) = T , where we take as above T =

It will be useful to adopt the following notation

(x) := u(x,s), u

(x) := u

(x,s),

where s ∈ [0, T ] and x ∈Ω. In the sum on the RHS of

(2.7) some cancellations are possible:

∑

i=0



Ω



∇u ·(x −x

) +

d −1





i−1

Ω



∇u

·(x −x

) +

d −1



−

N−1

∑

i=0

Ω



∇u

·[(x −x

i+1

) −(x −x

)]



−

Ω



∇u

·(x −x

) +

d −1



dx . (2.8)

For the ﬁrst and last term on the RHS of (2.8) we have



Ω



∇u

·(x −x

) +

d −1





≤ R

, (2.9)



Ω



∇u

·(x −x

) +

d −1





≤ R

. (2.10)

Moreover, for the terms in the sum on the RHS of

(2.8), we have



Ω



∇u

·(x

−x

i+1

)





≤ R

i+1,i

, (2.11)

for each i = 0, .. .,N.

For convenience, we postpone the proof of the ine-

qualities (2.9)-(2.11), see Lemma 2.2 below.

By deﬁnition of Γ

in (2.5) and R

in (2.3), clearly we

have

i−1

|∂

dΓ dt ≥

i−1

∂Ω

(x −x

) ·ν |∂

dΓ dt , (2.12)

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

for each i = 0, .. .,N.

Using the equation (2.7), the identity (2.8) and the es-

timates (2.9)-(2.12), we have



max

i=0,...,N



∑

i=0

i−1

|∂

dΓ dt ≥

2(T −R

−R

N,N−1

−···−R

1,0

−R

. (2.13)

Now, by assumption T > R

∑

N−1

i=1

i+1,i

+ R

, so

there exists a constant C = C

> 0, which depends on

T , such that

∑

i=0

i−1

|∂

dΓ dt ≥C

, (2.14)

which is exactly the observability inequality, as deﬁ-

ned in Deﬁnition 1.7.

We now prove the estimates (2.9)-(2.11); in particular

(2.9)-(2.10) and (2.11) follow respectively by i) and

ii) of the following Lemma.

Lemma 2.2. For each mild solution u ∈

C(R

(Ω)) ∩ C

(Ω)) of (1.4), the

following holds.

i) For each ξ ∈ R

and s ∈ R, then



Ω



∇u

·(x −ξ) +

d −1





≤ R

where R

= max{|x −ξ| : x ∈Ω}.

ii) For each ξ,η ∈ R

and s ∈ R

, then



Ω

(∇u

·(ξ −η))dx



≤ R

ξ,η

where R

ξ,η

= |ξ −η|.

Proof. i) By Chauchy-Schwarz inequality, we have



Ω



∇u

·(x −ξ) +

d −1





≤k u

k ∇u

·(·−ξ) +

d −1

≤

k∇u

·(·−ξ) +

d −1

;

(2.15)

here L

:= L

(Ω). Note that,

k∇u

·(·−ξ) +

d −1

= k ∇u

·(·−ξ) k

+(d −1)(∇u

·(·−ξ),u

)

(d −1)

k u

Since u = 0 on ∂Ω, then using Green’s identity the

middle term in the RHS of the previous equation is

equal to

Ω

(∇u

) ·(x −ξ) d x

Ω

(∇(u

)

) ·(x −ξ) d x

= −

Ω

)

(∇ ·(x −ξ))d x = −

k u

This implies

k ∇u

·(·−ξ) +

d −1

k ∇u

·(·−ξ) k



−(d −1)

(d −1)



k u

≤k ∇u

·(·−ξ) k

≤ R

k ∇u

since

−

d(d −1)

(d −1)

= −

< 0 ,

for all d ≥ 1.

Now returning to (2.15), we have



Ω



∇u

·(x −ξ) +

d −1





≤

k u

k ∇u

(k u

+ k ∇u

) = R

;

where the last inequality follows by the energy con-

servation (cfr. Corollary 1.5).

ii) The proof the second part of the Lemma is easier.

Indeed, by Cauchy-Schwarz inequality, we have



Ω

∇u

·(ξ −η) dx



≤k u

k ∇u

·(ξ −η) k

≤ R

ξ,η

k u

k ∇u

≤ R

ξ,η

;

where, the last inequality follows by the energy con-

servation.

2.1 The Role of {t

}

i=−1,...,N

One may wonder what is the role of the family

}

i=−1,...,N

, since in Theorem 2.1 only the sum T =

∑

i=0

−t

i−1

) appears.

To explain the role of these values, we have to recall

that if N = 0 (i.e. ﬁxed support control), Theorem

2.1 implies that the exact controllability holds for any

Variable Support Control for the Wave Equation - A Multiplier Approach

T > 2 max{|x −x

||x ∈ Ω}, where x

∈ R

is a ﬁxed

point. So, if for an index j ∈ {0,. ..,N} we have

−t

j−1

| > 2 max{|x −x

||x ∈ Ω}, (2.16)

then we can construct a control v such that suppv ⊂

×[t

j−1

] by using the ﬁxed support case of Theo-

rem 2.1. Indeed, ﬁx (w

) ∈ L

(Ω) ×H

−1

(Ω) and

let be w the unique weak solution of the problem (1.2)

for T = t

and v = 0; so by Theorem 1.6 we have

that (w(t

j−1

),w

j−1

)) is well deﬁned as an element

of L

(Ω) ×H

−1

(Ω). Since the inequality in (2.16)

holds, the ﬁxed case of Theorem 2.1 provides a cont-

rol ˜v such that the solution at time t = t

satisﬁes the

null condition; so after deﬁning v = 0 for t < t

j−1

< t < T and v = ˜v for t

j−1

< t < t

we have con-

structed a control for the initial condition (w

). So

if the inequality (2.16) holds for an index j the con-

trollability results follows by classical results, (see for

istance Theorem 6.1, Chapter 1 of (Lions, 1988)). In

the following Section we produce explicit examples

in which the inequality (2.16) is not satisﬁed by any

i = 0,... ,N; so our investigation produces new results

on controllability for the wave equation.

By the way, we point out that Theorem 2.1 allows

us to apply the Hilbert uniqueness method (or HUM,

see (Komornik and Loreti, 2005)-(Lions, 1988)); with

some effort one can prove that the control provided by

this method minimizes the energy of the control over

the possible controls (see Chapter 7 of (Lions, 1988)).

For this reason even in the case when (2.16) holds our

Theorem yields the existence of a minimizer control;

this remarkable property of the HUM control can be

useful in applications. For brevity we do not repro-

duce the needed calculations.

3 VARIABLE OBSERVATION

In this Section we state a fairly general observability

Theorem in which the subset Γ(t) of observation at

time t can vary at each time t ∈(0,T ).

As explained in Section 1, the family {Γ(t)}

t∈(0,T )

cannot be arbitrary and will be constructed in a si-

milar fashion to {Γ

}

i=0,...,N

(see (2.5) in Section 2).

To do this, let ϕ : [0, T ] → R

be a continuous and

piecewise differentiable curve in R

of ﬁnite length,

i.e.

L(ϕ) :=

|ϕ

(t)|dt < +∞. (3.1)

For such a ϕ, deﬁne

(t) = {x ∈ ∂Ω |(x −ϕ(t)) ·ν > 0}, (3.2)

[

t∈(0,T )

(t) ×{t}, (3.3)

= max

Ω

|x −ϕ(i)|, i = 0, T . (3.4)

Hereafter we assume that Σ

is H

d−1

⊗ L

measurable; for further discussion on this topic see

(Agresti et al., 2017).

Also, let P = {0 = t

−1

< t

< . ..t

N−1

< t

= T } be a

partition of the interval [0,T ]; deﬁne

ϕ, j

= ϕ(t

j−1

), (3.5)

ϕ, j

= {x ∈ ∂Ω |(x −x

ϕ, j

) ·ν > 0}, (3.6)

for all j = 0,. .. ,N. For future convenience, we set

[

j=0

ϕ, j

×(t

j−1

). (3.7)

In next theorem, we have to consider a sequence of

partitions {P

}

k∈N

of the interval [0,T ], so we will add

the upper index k in (3.5)-(3.6) in order to keep trace

of the dependence on P

; and we will set Σ

:= Σ

Now we are ready to state the main result of this

Section.

Theorem 3.1 (Variable Support Observability). Un-

der the above hypothesis, suppose there exists a se-

quence of partitions {P

}

k∈N

of the interval [0, T ],

such that sup

j−1

}∈P

−t

j−1

| & 0 as k % ∞ and

lim

k→∞



d−1

⊗L



∆Σ



= 0 , (3.8)

where P

= {0 = t

−1

< t

< ··· < t

= T }, L

is the

Lebesgue measure on R

and A∆B = (A\B)∪(B\A).

Furthermore, suppose that T veriﬁes

T > c

|ϕ

(t)|dt + c

. (3.9)

Then the system is exactly observable in time T (see

Deﬁnition 1.7) for Σ = Σ

For brevity we do not report the proof of Theorem

3.1; for the proof, other applications and further ex-

tension of this result we refer to (Agresti et al., 2017).

4 APPLICATIONS

In this Section we give some applications of Theo-

rems 2.1 and 3.1 in order to show the potentiality of

these results.

To begin, we focus our attention to Ω = B

:= {x ∈

||x| < 1}, i.e. the ball with center 0 and radius 1.

As usual, we denote with S

:= ∂B

the unit circle

with center 0.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

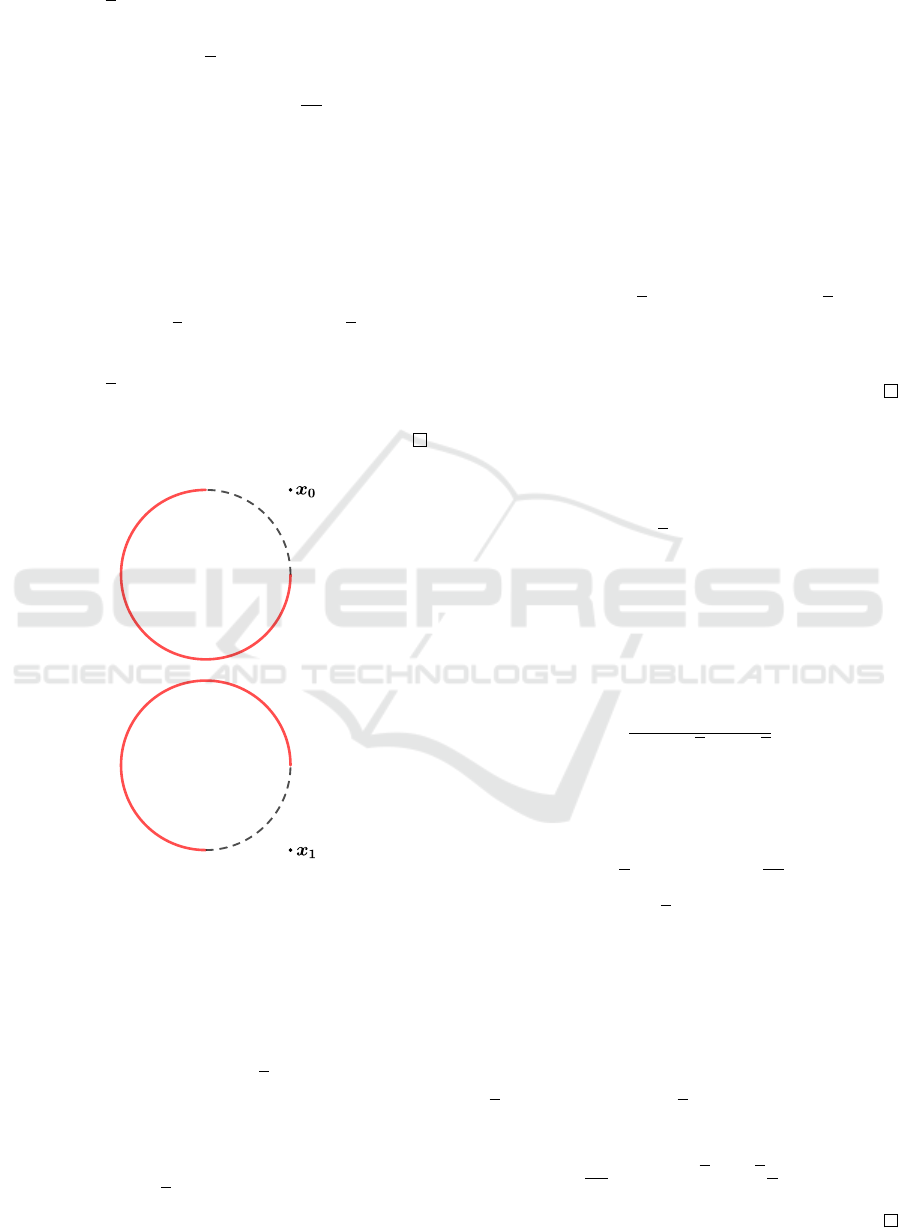
Corollary 4.1 (1-time alternating - Circle case). Let

T > 2(1 +

√

2) be a real number, deﬁne

z ∈ S



< arg z < 2π

, (4.1)

z ∈ S



0 < arg z <

3π

. (4.2)

Then the system (1.2) is exactly controllable for Ω =

, t

is an arbitrary element of (0,T ), and

Σ = d

×(0,t

)

[

×(t

,T ).

Proof. It is an easy consequence of Theorem 2.1 with

the choice x

= (1, 1) and x

= (1, −1). Indeed, by

(2.3)-(2.4) it is clear that

= R

√

2 + 1 , R

0,1

= 2

√

Moreover, the condition (2.6) in Theorem 2.1, implies

T > 2(1 +

√

2). Lastly, with simple geometrical con-

sideration, one can see Γ

= d

and Γ

= d

by (2.5);

see also Figure 1. This concludes the proof.

Figure 1: On the top (resp. bottom) we have represented

in red d

(resp. d

) and x

(resp. x

), to point out the con-

nection with the formula (2.5).

Remark 4.2. Note that in Corollary 4.1 there is no

assumption on the value t

∈ (0,T ); due to the dis-

cussion in Subsection 2.1 it is clear that Corollary 4.1

does not follow trivially by known results if

| < 2(1 +

√

2). (4.3)

We now extend Corollary 4.1 to the N-times alter-

nating case.

Corollary 4.3 (N-times alternating - Circle case). Let

T > 2(N + 1) + 2

√

2 be a real number and let d

be as in (4.1)-(4.2). Then the system (1.2) is exactly

controllable for Ω = B

, {t

}

i=0,...,N−1

any increasing

ﬁnite subfamily of (0,T ), and

Σ =

[

i=0,i∈2N

×(t

j−1

)

∪

[

i=0,i∈2N+1

×(t

j−1

)

. (4.4)

Proof. It is similar to the proof of Corollary 4.1. In

this case, we have to choose x

≡ x

= (1,1) if i is

even or x

≡ x

= (1, −1). Similar to Corollary 4.1,

we have

= R

√

2 + 1 , R

i,i+1

= 2

√

for all i = 0, .. .,N −1. As in the proof of Corollary

4.1, by (2.5) we have that Γ

≡ d

if i is even, other-

wise Γ

≡ d

and Σ is as in (4.4).

Remark 4.4. As did in Remark 4.2 for Corollary 4.1,

we observe that in Corollary 4.3 there is no assump-

tion on the values t

for i = 0,. .. ,N −1. In this case

we may require that

−t

j−1

| < 2(1 +

√

2), ∀j = 0, .. .,N ; (4.5)

to avoid triviality of the result in the previous Corol-

lary.

Below we give an interesting application of Theo-

rem 3.1.

Corollary 4.5. Let α ∈R

be a positive real number,

such that

α <

4(1 +

√

2) + π

√

. (4.6)

Then the system (1.2) is exactly controllable in time

T = π/(2α) with Ω = B

and Σ = ∪

t∈(0,T )

Γ(t) ×{t};

where

Γ(t) =

z ∈ S



+ αt < argz <

7π

+ αt

. (4.7)

Proof. Set ϕ(t) =

√

2(cos(αt),sin(αt)) for t ∈

(0,π/(2α)). It is easy to check that Γ(t) = Γ

(t)

(see Figure 2), to prove the Corollary we have only

to check the hypothesis of Theorem 3.1.

Indeed, it is clear that the condition (3.8) holds by

taking a sequence of partition P

= {t

}

j=0,...,k

with

= ( j/k)T and T := π/(2α).

By construction, the length of the curve is L(ϕ) =

√

2(π/2), and c

= 1 +

√

2 for i = 0, T . So condition

(3.9) is satisﬁed if

2α

> 2(1 +

√

2) +

√

, (4.8)

which is equivalent to (4.6).

Variable Support Control for the Wave Equation - A Multiplier Approach

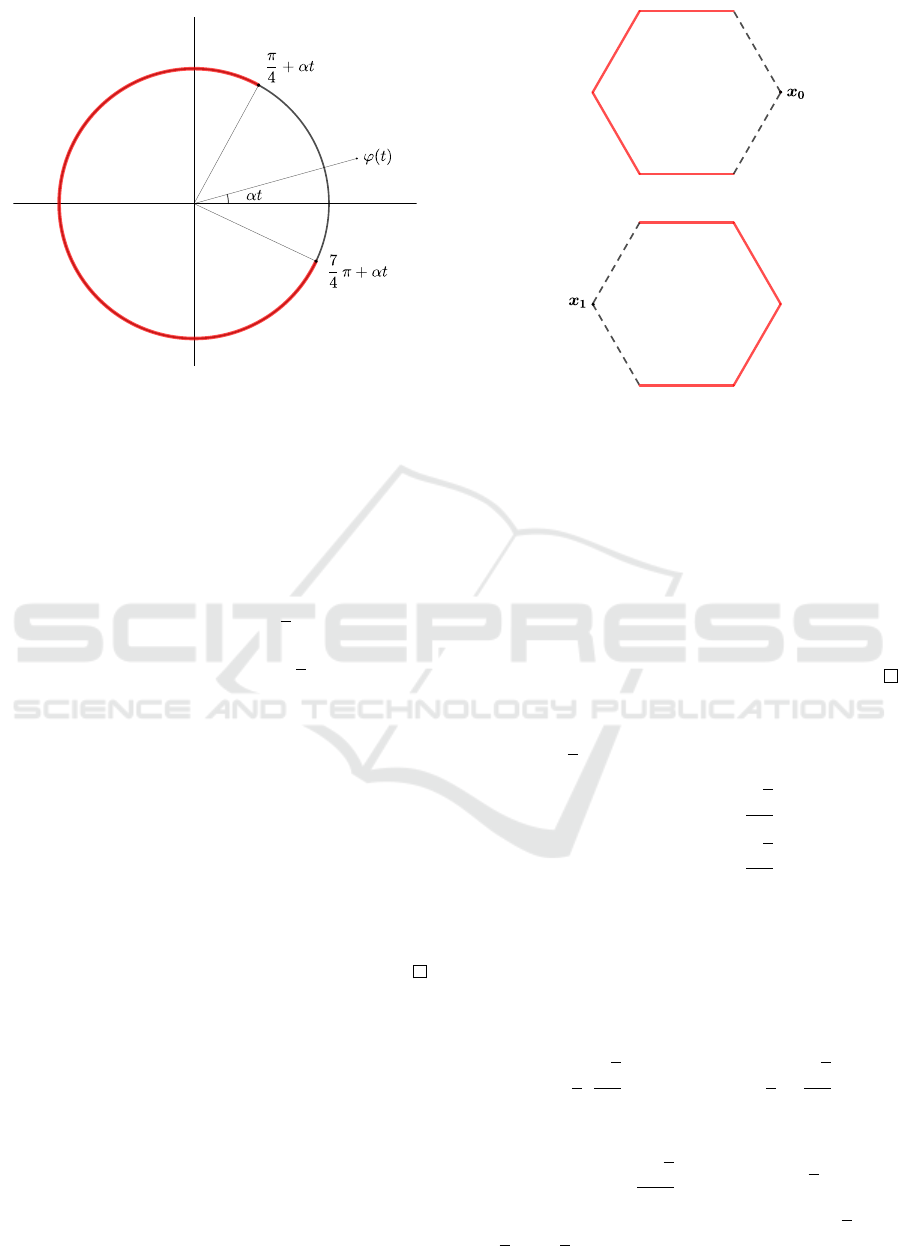
Figure 2: Construction of Γ

(t), in accordance with (3.2).

We now analyse a case of a convex domain; i.e.

the interior of the hexagon with side 1 and center 0, it

will be denoted by H ⊂ R

and we set E := ∂H .

In this situation, we have analogous result to Corolla-

ries 4.1, 4.3 and 4.5:

Corollary 4.6 (1-time alternating - Hexagon case I).

Let T > 6 be a real number, deﬁne

(x,y) ∈ E



x <

, (4.9)

(x,y) ∈ E



x > −

. (4.10)

Then the system (1.2) is exactly controllable for Ω =

H , t

is an arbitrary element of (0,T ), and

Σ = e

×(0,t

)

[

×(t

,T ).

Proof. As in the Proof of Corollary 4.1, we use The-

orem 2.1 with the choice x

= (1,0) and x

= (−1,0);

it is also clear that Γ

= e

and Γ

= e

by deﬁnition

(2.5) (see Figure 3).

Furthermore, by (2.3)-(2.4), we have

= R

0,1

= 2 ;

then by (2.6) the claim follows.

Corollary 4.7 (N-times alternating - Hexagon case).

Let T > 2(2 + N) be a real number and let e

as in (4.9)-(4.10). Then the system (1.2) is exactly

controllable for Ω = H , {t

}

i=0,...,N−1

any increasing

ﬁnite subfamily of (0,T ), and

Σ =

[

i=0,i∈2N

×(t

j−1

)

∪

[

i=0,i∈2N+1

×(t

j−1

)

Figure 3: On the top (resp. bottom) we have represented

in red e

(resp. e

) and x

(resp. x

), to point out the con-

nection with the formula (2.5).

Proof. Is similar to the proof of Corollaries 4.3 and

4.6.

In this case, we have to choose x

≡ x

= (1,0) if i

is even or x

≡ x

= (−1,0) otherwise; see Figure 3.

Moreover, by (2.3)-(2.4) we obtain

= R

i+1,i

= 2 .

Then condition (2.6) is equivalent to T > 4 + 2N =

2(2 + N) and the claim follows.

The last application consists in the following:

Corollary 4.8 (1-time alternating - Hexagon case II).

Let T > 5

√

3 be a real number, deﬁne

(x,y) ∈ E



y <

√

(x,y) ∈ E



y >

√

Then the system (1.2) is exactly controllable for Ω =

H , t

is an arbitrary element of (0,T ), and

Σ = e

×(0,t

)

[

×(t

,T ).

Proof. As in the Proof of Corollary 4.6, we use The-

orem 2.1 with the choice

√

, x

−

,−

√

By (2.3)-(2.4), we have

= R

√

, R

0,1

= 2

√

In this case, the condition (2.6) is T > 2(3

√

3)/2 +

√

3 = 5

√

3 as stated in the Corollary.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

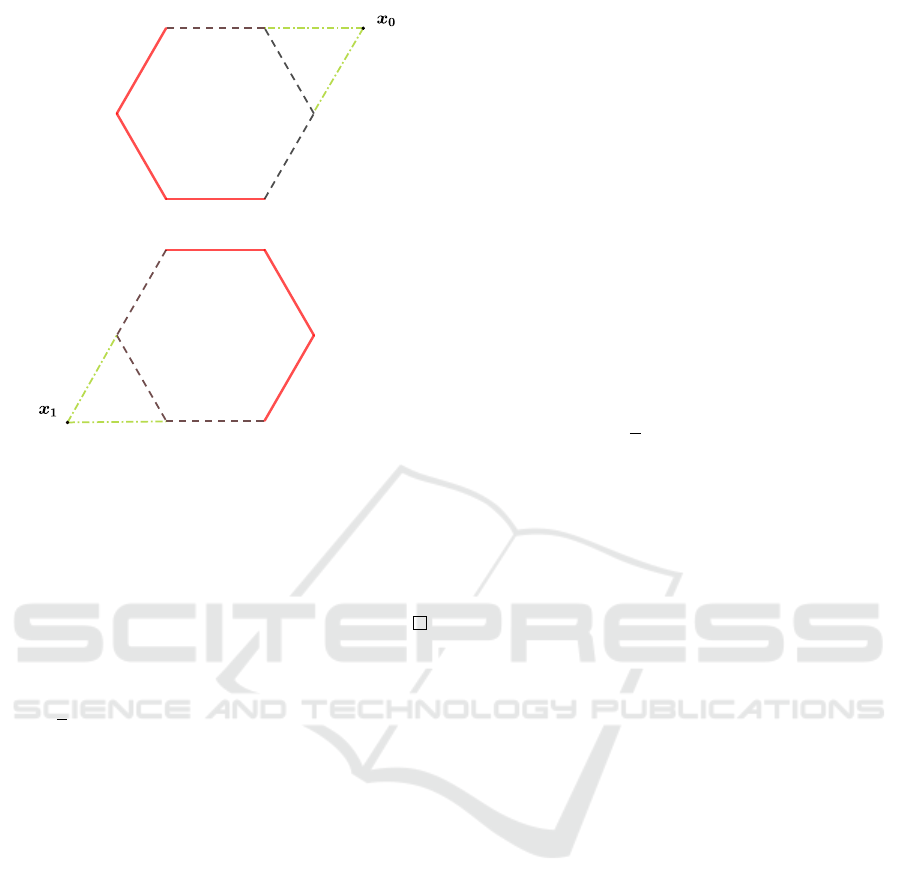
Figure 4: On the top (resp. bottom) we have represented

in red e

(resp. e

) and x

(resp. x

), to point out the con-

nection with the formula (2.5); the green lines are the pro-

longation of the hexagon sides.

Furthermore, with this choice of x

, by (2.5) one

can prove that Γ

= e

and Γ

= e

(see also Figure

4 for a geometrical construction); then the claim fol-

lows.

The analogous of Corollary 4.7 for the choice

of x

made in Corollary 4.8 can be easily

proven by the same argumentations (in this case

T >

√

3(3 + 2N)). In order to avoid repetition we do

not record the proof here; the same considerations

are valid for the content of Remarks 4.2 and 4.4.

We point out that Theorems 2.1 and 3.1 can be

applied to a very wide range of domains in R

for any

d > 1; we have chosen only two cases in this Section

in order to give a ﬂavour of the possible applications.

Note that, Theorem 3.1 needs the additional condition

(3.8), which is not in general immediate to prove,

though it can be proven to be valid for smooth Ω and

ϕ; this observation can be useful in applications.

5 CONCLUSIONS

To conclude we have shown that the exact controlla-

bility holds if T is sufﬁciently large and the subset of

observation Σ is suitable.

More speciﬁcally:

• Let {x

}

i=0...,N

be an arbitrary family of points in

, {t

}

i=−1,...,N

an increasing family of positive

numbers such that t

−1

= 0 and T := t

; then the

system (1.2) is exactly controllable if

T > R

N−1

∑

i=0

i+1,i

+ R

;

where R

i+1,i

are deﬁned in (2.3)-(2.4) and

Σ =

[

i=0

×(t

i−1

: = {x ∈ ∂Ω |(x −x

) ·ν > 0}.

See Theorem 2.1.

• Let ϕ : [0,T ] → R

be a continuous and piecewise

differentiable curve of ﬁnite length (see (3.1)). If

T > c

|ϕ

(t)|dt + c

;

: = max

x∈

Ω

|x −ϕ(i)|, i = 0, T ,

the system (1.2) is exactly controllable with

Σ =

[

t∈(0,T )

(t) ×{t},

(t) : = {x ∈ ∂Ω |(x −ϕ(t)) ·ν > 0}.

See Theorem 3.1.

These results can be helpful in engineering applica-

tions in which one has to control the evolution of a

structure (whose dynamics is governed by the wave

equation) by means of an action on a portion of the

boundary (see (Dessi et al., 2004)-(Carcaterra et al.,

2014)), but for structural reasons, one cannot act for a

long time on the same portion of the boundary, so that

the switch of the control is necessary.

Finally we mention that, the linear theory for ﬁxed

control support has been extended to nonlinear wave

equations, see for instance (Zuazua, 1993) or (Coron

and Tr

elat, 2006). With this in mind, we expect that

the variable support control results, proven before,

can be applied to show the exact controllability of sy-

stems driven by nonlinear wave equations with varia-

ble support control (see (Debnath, 1994) for explicit

physical examples).

REFERENCES

Agresti, A., Andreucci, D., and Loreti, P. (2017). Al-

ternating and variable controls. arXiv preprint

arXiv:1712.00797.

Bardos, C., Lebeau, G., and Rauch, J. (1992). Sharp sufﬁ-

cient conditions for the observation, control, and sta-

bilization of waves from the boundary. SIAM journal

on control and optimization, 30(5):1024–1065.

Variable Support Control for the Wave Equation - A Multiplier Approach

Carcaterra, A., Graziani, G., Pepe, G., and Roveri, N.

(2014). Cable oscillations in a streamﬂow: art in the

Tiber. Proceedings of the 9th International Confe-

rence on Structural Dynamics, A. Cunha, E. Caetano,

P. Ribeiro, G. Mller (eds.).

Castro, C., Micu, S., and M

unch, A. (2008). Numerical

approximation of the boundary control for the wave

equation with mixed ﬁnite elements in a square. IMA

Journal of Numerical Analysis, 28(1):186–214.

Coron, J.-M. and Tr

elat, E. (2006). Global steady-state sta-

bilization and controllability of 1D semilinear wave

equations. Communications in Contemporary Mathe-

matics, 8(04):535–567.

Debnath, L. (1994). Nonlinear water waves. Academic

Press.

Dessi, D., Carcaterra, A., and Diodati, G. (2004). Expe-

rimental investigation versus numerical simulation of

the dynamic response of a moored ﬂoating structure

to waves. Proceedings of the Institution of Mechani-

cal Engineers, Part M: Journal of Engineering for the

Maritime Environment, 218(3):153–165.

Evans, L. C. and Gariepy, R. F. (2015). Measure theory and

ﬁne properties of functions. CRC press.

Glowinski, R. and Lions, J.-L. (1995). Exact and approxi-

mate controllability for distributed parameter systems.

Acta numerica, 4:159–328.

Grisvard, P. (2011). Elliptic problems in nonsmooth dom-

ains, volume 69. SIAM.

Komornik, V. (1994). Exact controllability and stabiliza-

tion: the multiplier method, volume 36. Masson.

Komornik, V. and Loreti, P. (2005). Fourier series in control

theory. Springer Science & Business Media.

Lasiecka, I. and Triggiani, R. (1983). Regularity of hyper-

bolic equations under L

(0,T ; L

(Γ))-Dirichlet boun-

dary terms. Applied Mathematics and Optimization,

10(1):275–286.

Lions, J.-L. (1988). Contr

olabilit

e exacte, perturbations et

stabilisation de syst

emes distribu

es. tome 1. RMA, 8.

unch, A. (2005). A uniformly controllable and implicit

scheme for the 1-D wave equation. ESAIM: Mathema-

tical Modelling and Numerical Analysis, 39(2):377–

418.

Pazy, A. (2012). Semigroups of linear operators and appli-

cations to partial differential equations, volume 44.

Springer Science & Business Media.

Taylor, M. (2011). Partial differential equations I: Basic

Theory, volume 115. Applied Mathematical Sciences.

Tucsnak, M. and Weiss, G. (2009). Observation and cont-

rol for operator semigroups. Springer Science & Bu-

siness Media.

Zuazua, E. (1993). Exact controllability for semilinear

wave equations in one space dimension. In Annales

de l’Institut Henri Poincare (C) Non Linear Analysis,

volume 10, pages 109–129. Elsevier.

Zuazua, E. (2005). Propagation, observation, and control

of waves approximated by ﬁnite difference methods.

Siam Review, 47(2):197–243.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics