
TVL
1
Shape Approximation from Scattered 3D Data
E. Funk
1,2
, L. S. Dooley
1
and A. Boerner
2
1
Department of Computing and Communications, The Open University, Milton Keynes, U.K.
2
Department of Information Processing for Optical Systems, Institute of Optical Sensor Systems,
German Aerospace Center, Berlin, Germany
Keywords:
Shape Reconstruction, Radial Basis Function Interpolation, L
1
Total Variation Minimization, Iterative Large
Scale Optimization.
Abstract:
With the emergence in 3D sensors such as laser scanners and 3D reconstruction from cameras, large 3D point
clouds can now be sampled from physical objects within a scene. The raw 3D samples delivered by these
sensors however, contain only a limite d degree of information about the environment the objects exist in,
which means that further geometrical high-level modelling is essential. In addition, issues like sparse data
measurements, noise, missing samples due to occlusion, and the inherently huge datasets involved in such
representations makes this task extremely challenging. This paper addresses these issues by presenting a new
3D shape modelling framework for samples acquired from 3D sensor. Motivated by the success of nonlinear
kernel-based approximation techniques in the statistics domain, existing methods using radial basis functions
are applied to 3D object shape approximation. The task is framed as an optimization problem and is extended
using non-smooth L
1
total variation regularization. Appropriate convex energy functionals are constructed and
solved by applying the Alternating Direction Method of Multipliers approach, which is then extended using
Gauss-Seidel iterations. This significantly lowers the computational complexity involved in generating 3D
shape from 3D samples, while both numerical and qualitative analysis confirms the superior shape modelling
performance of this new framework compared with existing 3D shape reconstruction techniques.
1 INTRODUCTION
The analysis and perception of environments from
static or mobile 3D sensors is widely envisioned as
a major technological breakthrough and is expected
to herald a significant impact upon both society and
the economy in the future. As identified by the
German Federal Ministry of Education and Research
(H
¨
agele, 2011), spatial perception plays a pivotal role
in robotics, having an impact in many vital technolo-
gies in the fields of navigation, automotive, safety, se-
curity and human-robot-interaction. The key task in
spatial perception is the reconstruction of the shape
of the observed environment. Improvements in shape
reconstruction have direct impact on three fundamen-
tal research disciplines: self localization from cam-
era images (Canelhas et al., 2013), inspection in re-
mote sensing (Hirschm
¨
uller, 2011) and object recog-
nition (Canelhas, 2012). Applying 3D sensors in un-
controlled practical environments, however, leads to
strong noise and many data outliers. Homogeneous
surface colours and variable illumination conditions
lead to outliers and make it a difficult task to obtain
3D samples from over-exposed areas. Figure 1 shows
an example 3D point cloud obtained from a stereo
camera traversing a building. Many 3D points such as
marked by 1 suffer from strong noise. Occlusions
frequently occur in realistic scenes 2 and make
automated shape reconstruction even more challeng-
ing.
1
2
a) b)
Figure 1: a) The acquired 3D samples shown as a point
cloud. b) The scanned staircase as a photograph.
Dealing with noise and outliers inevitably in-
volves applying statistical techniques. In the last
decade, so-called kernel-based methods have become
well-accepted in statistical processing. Successful
294
Funk E., Dooley L. and Boerner A..
TVL1 Shape Approximation from Scattered 3D Data.
DOI: 10.5220/0005301802940304
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 294-304
ISBN: 978-989-758-091-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

techniques like deep learning or support vector ma-
chines exploit kernel-based methods in the fields of
machine learning and robotics for interpolation and
extrapolation (Sch
¨
olkopf and Smola, 2001). Since in-
terpolation and extrapolation are required when deal-
ing with error-prone 3D samples, the application of
kernel-based approximation techniques for shape ap-
proximation is especially relevant to this domain. The
initial aim was the investigation and development of a
suitable kernel for geometrical shape modelling from
noisy 3D samples.
Many indoor and urban outdoor environments
contain a rather small set of large planar shapes. This
information can be exploited to help reduce the noise
sensitivity leading to higher approximation accuracy.
Integrating piecewise smoothness into the approxima-
tion task has attracted a lot of interest in the image
processing community. A regularization technique,
also known as Total Variation (TV) minimization, is
applied to penalize strong variations in the colour val-
ues (Rudin et al., 1992; Getreuer, 2012). Pock et al.
(2011) extended the traditional TV approach to se-
cond derivatives of the filtered image pixels. Figure
2 shows the comparison of the TVL
1
approach with
state of the art statistical filtering techniques. The ex-
tension of the TV technique to 3D shapes, is still a
fertile area of research which is considered as the se-
cond aim in this paper.
(a) Ground truth (b) Input image
(c) Average
(d) Median (e) Huber (f) TV
Figure 2: Comparing the total variation minimization with
common statistical techniques for height maps filtering. Im-
age courtesy: Bredies et al., (2011).
A further challenge in automated shape approxi-
mation is the processing of large datasets. A realistic
dataset usually contains several millions of 3D points.
However, kernel-based and total variation techniques
suffer from high computational complexity prohibit-
ing their application to datasets which contain more
than a few thousand points (Bach et al., 2012). Such
methods normally require a set of linear equations
to be solved, which incurs O(N
3
) complexity. Even
if such a method could feasibly process N = 1,000
points in 10 ms, it would still take 115 days to process
1,000,000 points. This major complexity issue moti-
vated the third aim of this paper which is to develop
efficient strategies for handling non-smooth (L
1
) total
variation regularization on large datasets.
The remainder of this paper is organised as fol-
lows: A short overview of 3D shape reconstruction
approaches is provided in Section 2, including issues
such as approximation quality and stability. Section 3
discusses the three contributions of this work: i) ap-
plication of RBFs for implicit 3D shape modelling,
ii) integration of non-smooth TVL
1
regularization for
noise suppression, and iii) efficient optimization re-
ducing the computation complexity from O (N
3
) to
O(N). A critical quantitative analysis is then pre-
sented in Section 4, and concluding comments are
provided in Section 5.
2 LITERATURE REVIEW
The problem of reconstructing a surface of an object
from a set of scattered 3D points attracted a lot of at-
tention in the literature (Alexa et al., 2001; Ohtake
et al., 2003; Gomes et al., 2009) thus this section will
review existing techniques relating to the aims of this
paper, namely: shape representation using radial ba-
sis functions, statistical regularization model for noise
suppression, and efficient optimization.
2.1 Shape Reconstruction
Two general shape representation approaches for 3D
data currently exist: explicit and implicit representa-
tions.
Explicit Models are polygon meshes, non uni-
form B-Splines (NURBS) or Bezier curves (Hughes
et al., 2014). The research in computer graphics
lead to large number of software frameworks such
as OpenGL (Wolff, 2013) enabling the visualization
of parametric polygon meshes with the help of paral-
lel graphics hardware. For this reason initial research
on automated shape reconstruction from 3D scattered
points focused on the direct construction of triangle
meshes, also known as Delaunay-Triangulation. Me-
thods such as α shapes (Edelsbrunner and M
¨
ucke,
1994; Bernardini et al., 1999; Bodenm
¨
uller, 2009)
aim at create a polygonal mesh by connecting the in-
put samples by triangle edges. This however, leads to
inaccurate results when error-prone samples are pro-
vided. Other family of parametric shapes are NURBS
(Piegl and Tiller, 1997; Rogers, 2001) and Bezier
curves (Agoston, 2005), which are commonly used
in 3D modelling. These methods are able to create
smooth surfaces for non-uniform control point sets.
In order to apply these methods to automated shape
reconstruction from scattered 3D points, the surface is
TVL1ShapeApproximationfromScattered3DData
295

Figure 3: Smooth shape representation from scattered
points and surface orientations (arrows) via an implicit
function f (x).
defined as a graph in the parameter space. This makes
the problem non polynomial (NP) hard so its applica-
tion to larger datasets is prohibited (Zhao et al., 2001).
Implicit Models: Several state of the art tech-
niques represent a shape implicitly by an indicator
function f (x) to indicate inside f (x) < 0 or outside
f (x) > 0 of the object with x ∈ R
3
as the location in
the 3D space. The surface of the object is the set of all
x, where f gives zero. Figure 3 illustrates an implicit
shape where the dots indicate the samples on the sur-
face ( f (x) = 0) and the point orientations the normal
of the shape (∇ f (x
i
) = n
i
). This representation allows
to extract smooth surfaces from irregularly sampled,
noisy and incomplete datasets (Gomes et al., 2009).
Facing the noise sensibility issues of Delaunay-
Triangulation techniques, Alexa et al. proposed to
apply moving least squares (MLS) for smoothing (av-
eraging) the point samples prior to reconstructing a
mesh via a Delaunay-Triangulation technique (Alexa
et al., 2001). A simple implicit shape is for instance
a plane, defined by its four parameters n
T
x + d = 0
with n ∈ R
3
as the plane normal vector and d as off-
set to the origin along n. Defining a shape function as
f (x) = b(x)
T
u with b(x) = (x
1
,x
2
,x
3
,1) and u as the
plane coefficients u = (n
1
,n
2
,n
3
,d) enables to find u
via a regression task (Alexa et al., 2003). Similarly,
Guennebaud extended the shape model to spheres
and proposed the popular Algebraic Point Set Sur-
faces (APSS) method (Guennebaud and Gross, 2007).
Ohtake et al. and Oztireli et al. addressed the over
smoothing issues by applying non linear regression
for shape approximation (Ohtake et al., 2003; Oztireli
et al., 2009). The MLS techniques are well capable of
filtering data sets with moderate or small noise. How-
ever, it is still not feasible for realistic datasets, as in-
troduced in Figure 1.
Implicit Models with Basis Functions: Moti-
vated by the drawbacks of MLS approaches, Calakli
and Taubin proposed to apply a global optimization
process (Calakli and Taubin, 2011). Acquired 3D
samples are structured with an octree and the implicit
values of f (x) are distributed on the corners of the oc-
tree nodes (voxels). This approach enables large holes
to be closed and allows to handle sparse spatial sam-
ples which lead to isolated fragments when MLS is
applied. A similar approach is proposed by Kazhdan
and Hoppe, where the voxel corners are the B-Splines
control points (Kazhdan and Hoppe, 2013). Both ap-
proaches suffer from the fundamental drawback that
a priori information is required from an expert user to
define the depth of the octree structure, which makes
using it in automated applications very difficult.
Another family of implicit surface reconstruction
algorithms uses smooth radial basis functions (RBF).
The main difference between RBF based approxima-
tion and discrete octree models (Calakli and Taubin,
2011; Kazhdan and Hoppe, 2013) is that RBFs are
not necessarily centred on the octree leaves but di-
rectly on the samples. This reduces the risk of ap-
plying inappropriate discretisation and to lose shape
details (Gomes et al., 2009; Carr et al., 2001).
Novel approaches (Zach et al., 2007) propose to
create a dense grid of a user specified resolution and
to use the L
1
norm to penalize the changes between
the implicit grid corner values. Accurate results are
achieved when a fine grid is applied, although the ap-
proach does not consider the smoothness of the se-
cond derivative of the shape leading to non smooth
reconstruction. Another drawback of the method is
that it is restricted to small and compact objects since
the computation time and memory consumption for
the dense grid quickly become prohibitive.
Bredies et al. proposed to apply so-called gene-
ralized total variation minimization on depth images
to penalize the variance in the second derivatives lead-
ing to piecewise smooth shapes (Figure 2). The ac-
curacy of the method motivates its extension to 3D
shapes, which has not been reported in the literature.
Bredies et al. state that the stability of the approach
heavily depends on the smoothness of the data, which
is feasible when smooth RBFs are applied (Bredies
et al., 2010). Thus, when developing an RBF based
approximation model with a TV regularization, the
choice of an appropriate RBFs type is crucial.
With a popular RBF example being Gaussian,
which is of infinite differential degree, but tends to
smooth out fine detail, Wahba studied the application
of Duchon’s Thin Plate Splines (Duchon, 1977) that
facilitate control of the smoothness degree (Wahba,
1990). Due to its global definition domain, Thin Plate
Splines do not result in sparse systems and lead to
complex computations. Even more adverse, a change
of a single RBF centre affects the complete shape
model in the full approximation domain, which is not
the case for RBF using compact support such as Gaus-
sians. Later, Wendland proposed several RBF types
with compact support of minimal smoothness degree
(Wendland, 1995). Wendland’s RBFs also control
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
296

the smoothness of the approximated function and still
lead to sparse and efficient linear regression systems.
Moreover, as presented in Section 3, the smaller the
smoothness degree the more stable is the regression
process. The Thin Plate RBFs, however, have been
shown to achieve superior approximation quality in
the presence of noise (Tennakoon et al., 2013). Impor-
tant aspects when selecting an appropriate RBF type
are presented in Section 3.1.
2.2 Efficient L
1
Optimization
Extending the shape approximation with a L
1
penalty
requires more advanced techniques to solve the opti-
mization task. This issue has been discussed for some
time in the statistics and numerical optimization com-
munity. However, efficient techniques being capable
of dealing with thousands or millions of data samples
are in the current research focus.
Tibshirani proposed the Least Absolute Shrink-
age and Selection (Lasso) technique to minimize cost
functions such as
k y − Kα k
2
2
+ k α k
1
(1)
with k α k
1
=
∑
N
j
|α
i
| enabling its application on
images with several hundreds of thousands entries in
α (Tibshirani, 1994). This form is common for regres-
sion problems, where the signal y is approximated lin-
early by the model matrix K. The additional k · k
1
penalty term enforces only a small amount of non ze-
ros entries in α. This behaviour is suitable for prob-
lems where the vector α is expected to have many zero
entries. A common application is for example signal
approximation by only a small set of frequencies rep-
resented by α.
When representing a shape with N RBFs
f (x) =
N
∑
i
ϕ(x,x
i
)α
i
= k
T
α (2)
with k
i
= ϕ(x,x
i
) its second derivatives are penalized
by k Dα k
1
with D
j,i
= ∂
2
xx
ϕ(x
j
,x
i
). This way k Dα k
1
penalizes the amount of non smooth regions in the
extracted model. However, since the entries in Dα
are not separated as it is the case in (1), such prob-
lems are more difficult to solve and using the Lasso
technique is not possible. Initially, interior active sets
methods have been applied to solve the TVL
1
objec-
tive (Alizadeh et al., 2003). Chen et al. additionally
demonstrated that the efficiency of primal-dual me-
thods is of magnitudes higher than of the interior me-
thods (Chen et al., 2010). Also Goldstein et al. pro-
posed a primal-dual approach known as the Bregman
Split (Bregman, 1967) to separate the smooth data
term f
d
=k y−Kα k
2
2
from the non smooth regulariza-
tion term f
r
=k Dα k
1
and to optimize each of them
independently (Goldstein and Osher, 2009). Boyd et
al. extended the Bregman Split approach by Dykstra’s
alternating projections technique (Dykstra, 1982) and
proposed the Alternating Direction Method of Mul-
tipliers (ADMM) (Boyd et al., 2011), which further
improves the convergence. Discussions related to ap-
plications of ADMM are reported by Parikh and Boyd
(2014).
The bottleneck of ADMM is the minimization
of the smooth part f
d
=k y − Kα k
2
2
. Solving this
for α with efficient Cholesky factorization suffers
from a complexity of O(N
3
). However, an iterative
linear solver such as Jacobian or Gauss-Seidel may
reduce the complexity to O(N) as discussed by Saad
or Friedman et al. relating to L
1
regularization (Saad,
2003; Friedman et al., 2010). Nevertheless, further
investigations on the applicability of iterative linear
solvers and ADMM on 3D shape modelling do not
exist.
2.3 Summary
The presented state of the art in robust shape approxi-
mation and optimization methods covers several ap-
propriate options for investigation. Table 1 shows
the seminal methods summarizing the benefits and
drawbacks of each technique. The TVL
1
approach
(Bredies et al., 2010) delivers high quality with arte-
facts such as missing data, noise, outliers, or sharp
edges in the image domain. This technique, how-
ever, suffers from high computational complexity and
needs to be extended to 3D shape approximation.
Section 2.2 states that the ADMM technique is ex-
pected to outperform the efficiency of existing TVL
1
algorithms when extended with an iterative solver.
The next Section investigates the impact of dif-
ferent RBFs applied for signal and shape approxima-
tion from scattered 3D points before the new ADMM
technique for TVL
1
optimization on large datasets is
presented.
3 THE METHOD
The first part of this section pursues the first research
objective and discusses the fundamentals of RBF
based approximation and compares different types of
RBFs with respect to quality and stability when least
squares optimization is performed. Section 3.2 ap-
plies the proposed RBFs and defines the convex opti-
mization task to perform shape reconstruction from
scattered 3D samples augmented with a TV regular-
ization term. The last part of this section presents the
TVL1ShapeApproximationfromScattered3DData
297

Table 1: Shape approximation comparison. Here + indicates that a method is moderately successful in a particular aspect,
and ++ indicates that a method is very successful.
Method Missing Data Noise Outliers Comput. Speed Sharp Edges
α shapes (Edelsbrunner and M
¨
ucke, 1994) ++ +
Adaptive α shapes (Bernardini et al.,
1999)
+ ++ +
APSS (Guennebaud and Gross, 2007) + + + +
Smooth Signed Distance (Calakli and
Taubin, 2011)
++ + + +
Poisson (Kazhdan and Hoppe, 2013)
++ + + +
TVL
1
Depth Fusion (Bredies et al., 2010)
++ ++ ++ ++
developed optimization technique that allows to re-
duce the computational complexity while still being
able to solve TVL
1
regularized approximation tasks.
3.1 Interpolation with Radial Basis
Functions
When approximating any signal from a set of mea-
surements, the general aim is to determine a function
f : R
d
7→ R from a set of N sample values at x
i
∈ R
d
.
The core idea of RBF based approximation is that the
function f (x) may be represented by a linear combi-
nation of M weighted functions such as
f (x) =
M
∑
j
ϕ(x,x
j
)α
j
. (3)
Each of the basis functions ϕ(x,x
j
) is centered
at each measurement x
j
, and basically computes the
similarity between x and x
j
∈ R
d
. One possible form
for ϕ is a Gaussian ϕ(x,x
j
) = e
−kx−x
j
k/σ
with σ influ-
encing the width of the support.
The underlying idea of RBF approximation is il-
lustrated for a one-dimensional signal in Figure 4,
where f is defined as a sum of all given Gaussians
with their weights α
j
respectively. Usually it is as-
sumed that the widths σ of the basis functions are
known a priori so only the weighting factors α
j
are
to be found, leading to f (x).
The task is therefore to perform regression over N
samples and to find M weights via minimization of
Figure 4: Illustrative example of a function f (red line) con-
structed by a weighted linear combination of Gaussian ra-
dial basis functions.
min
α
N
∑
i
(y
i
−
M
∑
j
α
j
ϕ(x
i
,x
j
))
2
where y
i
is the i-th measured sample at position x
i
.
This can also be rewritten in matrix-vector form as:
min
α
k y − Kα k
2
2
. (4)
where K is often referred to as the design matrix or
the kernel matrix with K
i, j
= ϕ(x
i
,x
j
). The solution is
obtained via
α = A
−1
K
T
y (5)
with A = (K
T
K). This is the well known linear least
squares regression. Note that the function f (x) itself
is not restricted to be linear.
In the last two decades several types of RBFs have
been proposed for different applications. For the ap-
plication on shape approximation three RBF types are
investigated. i) The Gaussian which is the state of
the art, ii) Thin-Plate splines (Duchon, 1977) with
global smooth properties and the iii) compactly sup-
ported RBFs (CSRBFS) (Wendland, 1995) which en-
able sparse regression systems to be created and to
control the smoothness of the solution. Table 2 shows
the three types of the investigated RBFs with the cor-
responding explicit forms for data dimension d = 3.
Note that the scaling of each RBF type is achieved by
scaling the argument
ϕ
s
(r) = ϕ(
r
s
) with r =k x
i
− x
j
k
2
. (6)
In order to make a systematic decision which RBF
type is best suited for the underlying application,
Table 2: Investigated radial basis functions for data dimen-
sion d = 3.
Type ϕ
(
r) Cont. m
Gaussian e
−r
2
C
∞
CSRBF (1 − r)
2
+
C
0
(1 − r)
4
+
(4r + 1) C
2
(1 − r)
6
+
(35r
2
+ 18r + 1) C
4
Thin-Plate r
2m−3
C
m
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
298
the stability and the approximation quality is consid-
ered. When solving for α in (5), the condition of K
cond K = |
λ
max
λ
min
| plays an important role. λ
min
and
λ
max
are the minimal and maximal eigenvalues of K
respectively. In practice, it is not feasible to evalu-
ate the condition number on large systems since the
computation of the eigenvalues has a complexity of
O(N
3
). Therefore, a generalized approach to assess
the stability a priori is proposed.
Considering the minimal distance between two
samples as q
x
:=
1
2
min
j6=i
k x
i
− x
j
k
2
and interpret-
ing f (x) =
∑
M
j
ϕ(x)α
j
as a transfer function, it is
proposed to analyse the system behaviour in the fre-
quency domain. The key to this is the Fourier-Bessel
transform of ϕ(r) (Wendland, 2004). Interpreting the
frequency ω as the minimal distance q
x
between the
approximated samples provides the best-case stabil-
ity of the regression model without having to perform
experiments on data. More practically, the boundaries
for the lowest eigenvalue are discussed and put in re-
lation to the expected sample radius q
x
. This enables
qualitative assessment of a basis function without per-
forming any numerical experiments. Regarding the
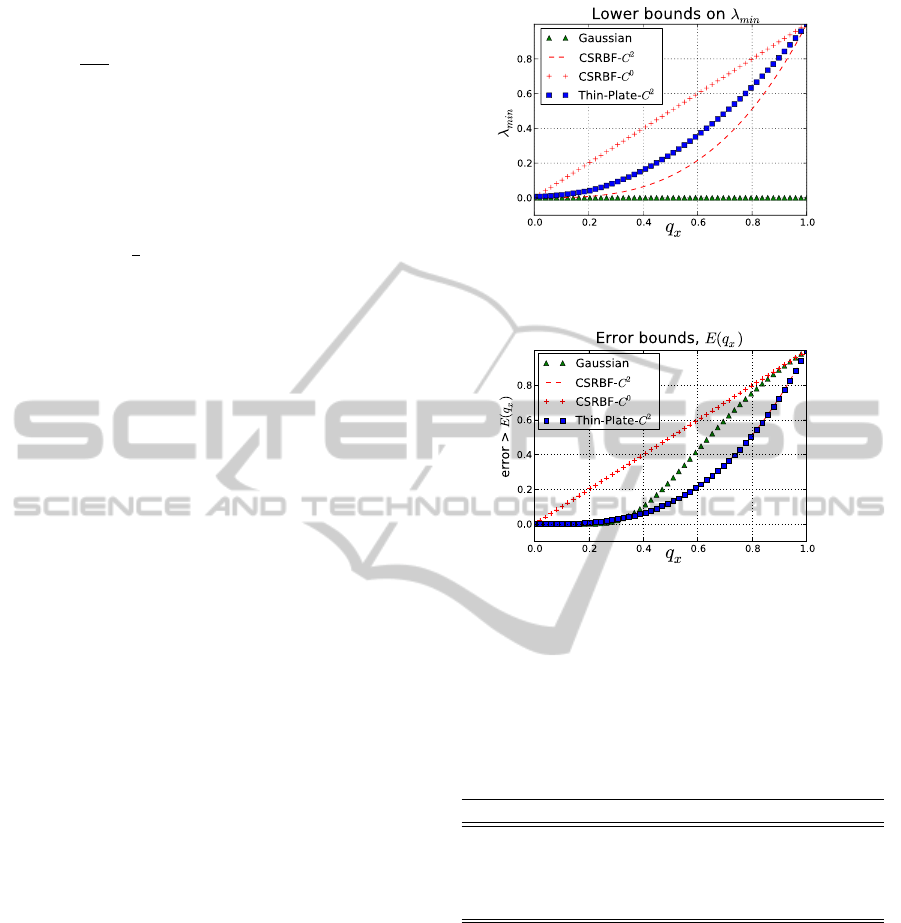
stability evaluation presented in Figure 5, the Thin-
Plate RBF is the only type, which remains stable for
all q
x
. Depending on the smoothness, CSRBF with C
0
and C
2
follow. The Gaussian RBF is the least stable
basis function with λ
min
slightly below zero.
Another important aspect when selecting an RBF
type is the approximation quality. Similarly to the
case of stability assessment, numerical experiments
often only indicate the behaviour of the RBFs re-
stricted to the given dataset. Thus, it is proposed to
appraise the theoretical error bounds in a similar way,
as has been shown with the generalized stability. The
diagram in Figure 6 presents the best achievable error
up to a positive scale factor for each RBF type given
the sampling density q
x
. It is clear that the higher the
sampling density, the better the approximation qual-
ity. Notably, the CSRBF-C
2
achieves higher quality
than other compact RBFs with lower sampling den-
sity q
x
and is very similar (overlays) with the global
Thin-Plate RBF.
This evaluation indicates the superior perfor-
mance of the Thin-Plate RBF, though this is not ap-
plicable in most realistic applications because the sup-
port is not restricted to the neighbouring domain. Fur-
thermore, the presented evaluations claim that ap-
plying the compactly supported RBFs with C
2
or
C
0
achieves comparable properties. Table 3 shows
the summarized investigation results, where a higher
number of plus signs reflect better performance. Ac-
cording to the evaluation it is clear that CSRBF is
more stable and more accurate than the Gaussian
Figure 5: The lower bounds for λ
min
(higher is better) of dif-
ferent RBFs depending on the normalized sampling radius
q
x
, d = 3 and different continuities C
m
.
Figure 6: The lower bounds (lower is better) for the approx-
imation error of each RBF type.
RBFs and provides comparable performance to the
Thin-Plate splines without requiring global support.
These key observations imply that using CSRBF for
3D data approximation is an attractive option which
will now be examined in the next Section.
Table 3: Comparative overview of the RBF models.
Gaussian Thin Plate CS-RBF
Stability + + + + + +
Approximation + + ++ + + + +
Smoothness + + + + + + + (+)
C
2
Efficiency + + +
3.2 Shape Reconstruction from
Scattered Points
The principal idea of shape modelling with RBF is
to extract an implicit function which represents the
shape by its zero value as introduced in Figure 3.
More formally, an algebraic function f (x), f : R
3
7→ R
needs to be constructed by regression. Given a set of
measured 3D points, the task is further to find a func-
tion f (x) which returns zero on every i-th sample x
i
and interpolates well between the samples. Since the
zero level alone does not provide information about
TVL1ShapeApproximationfromScattered3DData
299

Figure 7: Example sparse matrices K
∇
and K for (10) when
CSRBF is applied.
the orientation of the surface, the surface normals n
i
at every sample are used as constraints for the gradi-
ent ∇ f (x) wrt. x. The task is now to find f (x
i
) = 0
giving zero at every sample position and ∇ f (x
i
) = n
i
.
Integrating all this information, a convex cost func-
tional is defined.
min
α
N
∑
i
k f (x
i
) k
2
2
+ k n
i
− ∇ f (x
i
) k
2
2
(7)
To simplify the optimization problem the normaliza-
tion term k ∇ f (x
i
) k
2
= 1 is omitted. In order to obtain
the gradient ∇ f , only the gradient of ϕ needs to be
computed, which is precomputed analytically. Putting
(7) into matrix notation leads to the short form of the
cost function
min
α
α
α
k Kα
α
α k
2
2
+ k n − K
∇
α k
2
2
. (8)
The matrix K contains the values of the RBFs K
n,m
=
ϕ(x
n
,x
m
) ∈ R and K
∇n,m
= ∇ϕ(x
n
,x
m
) ∈ R
3
repre-
sents the derivatives of ϕ wrt. x
n
. The matrices are of
sizes K ∈ R
N×M
and K
∇
∈ R
3N×M
. At this point it be-
comes clear that radial basis functions with local sup-
port return for distant points x
n
,x
m
zeros which leads
to sparse matrices K and K
∇
improving the storage
and the computation efficiency. Figure 7 shows ex-
ample matrices K and K
∇
when a RBF with compact
support is applied. Black dots illustrate the non-zero
matrix values.
Figure 8 shows an example of applying CSRBF-
C
2
on a synthetic point set. The red line in Figure 8a)
indicates the cut-plane at which the Figure 8b) has
been rendered, while Figure 8c) shows the 3D shape
reconstruction.
Next, it is proposed to extend the cost term with
an additional total variation regularization term en-
forcing piecewise smoothness. In computer vision it
is accepted practise (Getreuer, 2012) to measure the
total variation by computing the Frobenius norm of
a Hessian matrix. In contrast, it is proposed to com-
pute the second derivatives with respect to the radius
r of the RBF ϕ(r). Comparing the single computa-
tion ∂
2
rr
ϕ(r) to the evaluation of the 3 × 3 Hessian
matrix with nine elements, this reduces the computa-
tional cost by a factor of nine and is easier to compute
analytically. Similar to the case when computing the
gradients of f , the second derivative is also a sum of
derived RBFs
TV (x) =
M
∑
m
∂
2
rr
ϕ(r)α
m
(9)
with r =k x
m
− x k
2
. Applying the TV regularization,
the cost function becomes
min
α
k Kα k
2
2
+ k n − K
∇
α k
2
2
+λ k Dα k
1
(10)
with D
n,m
= ∂
2
rr
ϕ(x
n
,x
m
) and λ as the weighting of
the regularization term. The factors α
m
corresponding
to the largest eigenvalue of D are attenuated the most
while weights lying in the kernel of D, are not affected
at all. Figure 9 shows an example when the input sam-
ples have been perturbed by noise (Figure 10a) and
the shape is reconstructed via a) simple least squares
(LSQ) and b) TV L
1
. In both images the red colour
corresponds to the TV cost intensity (9). Clearly,
when applying TV minimization the shape accuracy
of the reconstruction is improved and the red TV in-
tensity is reduced significantly.
Increasing the normally distributed sample noise
up to σ ≈ 30% of the bounding box, the effect of the
regularization is demonstrated in Figure 10. While the
simple LSQ model does not achieve a smooth shape
(Figure 10b) the new regularized approach in Figure
10c) shows considerable perceptual improvement in
terms of the quality of the shape reconstruction.
In the next section, the proposed numerical tech-
nique to efficiently solve the TVL
1
task is presented.
3.3 TVL
1
Solver
To minimize the task (10) it is proposed to apply the
Lagrangian approach from the Alternating Direction
Method of Multipliers (ADMM) (Boyd et al., 2011).
Formally, (10) is restated to
a) b) c)
Figure 8: a) Synthetic input points, b) the cut plane visu-
alizing f (x) as red ( f < 0) green ( f > 0), c) reconstructed
shape from a).
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
300

a) b) c)
Figure 10: a) Noisy 3D samples of the step function. b) Direct LSQ. c) TV L
1
regularized approximation.
a) b)
Figure 9: a) The TV cost (red) overlaid with the unregular-
ized shape obtained via LSQ. b) The reduced TV cost (less
red colour) after performing regularized approximation fol-
lowing (10).
min
α,z
L(α,z) = f
1
(α) + f
2
(z)+
b
T
(Dα − z) +
ρ
2
k Dα − z k
2
2
(11)
where f
1
(α) is the data part from (10) depending on
α, and f
2
(z) = λ k z k
1
is the non-smooth regular-
ization part weighted by λ. The basic approach is
to minimize for α, then for z iteratively. The terms
b
T
(Dα − z) and k Dα − z k
2
make sure that Dα is
close to z after an iteration finishes reducing the du-
ality gap. This restriction is controlled by ρ which is
usually a large scalar. The iterative optimization pro-
cess between α and z is summarized in Algorithm 1.
The minimization for z involves a sub gradient over
k · k
1
and its solution is known as the shrinkage oper-
ator (Efron et al., 2004) being applied on each element
z
i
independently:
z
i
= shrink(a, b)
= a − b · sign(b − a)
+
where a =
b
i
ρ
+ (Dα)
i
, b =
λ
ρ
(12)
with (Dα)
i
as the i-th element of the vector Dα and
sign(b − a)
+
gives 1 if b > a and zero otherwise.
Algorithm 1: ADMM for L
1
approximation
1. Solve for α:
(K
T
∇
K
∇
+ K
T
K + ρD
T
D)α = K
T
∇
n + D
T
(ρz − b).
2. Evaluate: z
k+1
i
= shrink(
b
i
ρ
+ (Dα)
i
,λ/ρ)
3. Evaluate: b
k+1
:= b
k
+ (Dα
k+1
− z
k+1
)ρ
While steps 2 and 3 are direct evaluations and can be
performed in parallel after Dα
k+1
has been precom-
puted, step 1 incurs high computational complexity.
It is proposed to solve α
k+1
via Gauss-Seidel itera-
tions well known from large scale linear system opti-
mization (Saad, 2003). However, the standard Gauss-
Seidel process suffers from difficult convergence con-
ditions. Thus, successive over relaxation (SOR) is ap-
plied with a weight factor ω. By applying SOR in step
1 Algorithm 1 is solved via:
α
k+1
i
= α
k
i
+ ω
y
i
− (K
T
∇i
K
∇
+ K
T
i
K + ρD
T
i
D)α
k
K
T
∇i
K
∇i
+ K
T
i
K
i
+ ρD
T
i
D
i
(13)
with y
i
= K
T
∇i
n + D
T
i
(zρ − b) and ith columns of a
matrix respectively. Considering that K
∇
, K and D
are sparse when CSRBF is applied, the computation
is reduced to Algorithm 2.
Algorithm 2: Matrix free TVL
1
.
1. For each RBF centre α
i
compute:
(a) Find all neighbouring centres and all neighbou-
ring samples located in the support of α
i
.
(b) Compute the equation (13) using only the
collected neighbours.
(c) Precompute Dα with the new α
k+1
i
.
2. Evaluate: z
k+1
i
= shrink(
b
i
ρ
+ (Dα)
i
,λ/ρ)
3. Evaluate: b
k+1
:= b
k
+ (Dα
k+1
− z
k+1
)ρ
The optimization is controlled by two important
parameters: ω for the successive over relaxation and
the RBF scaling s, as introduced in table 2 and (6).
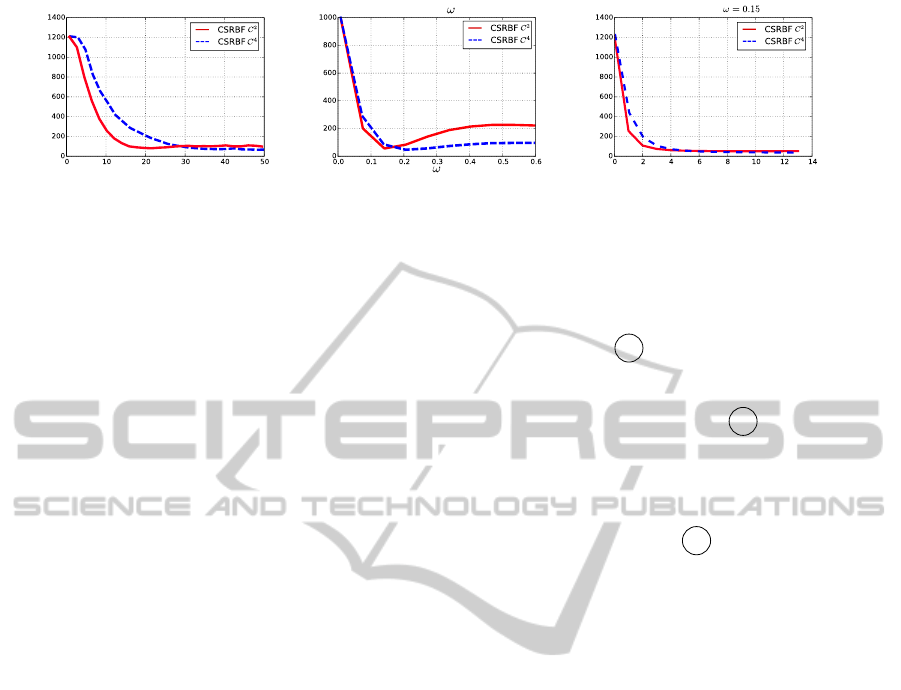
Figure 11 shows the effect of these parameters on the
approximation quality and the achieved convergence
rates. The experiments have been performed on the
synthetic dataset from Figure 8. Figure 11a) illus-
trates the approximation quality over the scaling s, the
quality attains its optimum when s = 10 is reached.
This observation corresponds to the generalized in-
vestigations from Figure 6, where s = 10 is q
x
= 0.1.
Furthermore, the empirical impact analysis of the over
TVL1ShapeApproximationfromScattered3DData
301
Minimal points within RBF support
Residuum
s
Residuum
Effect of
Iteration
Residuum
Convergence
a) b) c)
Figure 11: a) The impact of the scaling parameter s, b) the over relaxation weighting ω, c) convergence behavior for ω = 0.15
when CSRBF-C
2
or CSRBF-C
4
are applied.
relaxation parameter ω on the convergence concludes,
that ω ≤ 0.15 enables to remove the instability issues
for CSRBF-C
2
and CSRBF-C
4
when SOR is applied.
Note that when applying the Gaussian RBF, ω is re-
quired to be very small (ω ≈ 1e − 3), leading to an
impractically high number of iterations. This fact is
a consequence of the stability properties of the Gaus-
sian, investigated in Section 3.1.
The next section evaluates the proposed TVL
1
shape approximation framework with respect to ex-
isting methods by applying the algorithms on a large
dataset with an existing ground truth.
4 EVALUATION
This Section evaluates the proposed shape recon-
struction framework on different datasets and com-
pares it with two successful surface reconstruction
techniques: The Poisson approximation (Kazhdan
and Hoppe, 2013), and the Smooth-Signed-Distance
(SSD) algorithm (Calakli and Taubin, 2011). The
selected methods have been identified as success-
ful techniques for shape reconstruction under strong
noise. Both use the implicit model to represent the
shapes, however, in contrast to the presented work the
compared methods structure the data via an octree of
predefined depth and apply discrete optimization via
finite differences to extract the zero level of the sur-
face.
The analysis uses a 3D point cloud as the input,
and since 3D samples with a ground truth were not
available, a virtual camera flight was simulated in or-
der to generate error prone data with an established
ground truth. The simulation of the moving camera
and noisy 3D measurements were achieved by extend-
ing the CAD software Blender (Open Source Com-
munity, 2014). This enabled different noise levels
on the measurements to be applied and provided an
accurate model of the observed environment. Figure
12a) shows the ground truth model used for the simu-
lated measurements in assessing the quality of recon-
structed 3D shapes in Figure 12e). An outdoor scene
was selected since similar environments are used in
many robotic applications. The facade consisted of
large planar areas with a number of sharp edges as
identified in point 1 . The proposed TVL
1
tech-
nique performs significantly better than the Poisson
approach and similarly well compared to SSD. Dur-
ing the simulation several areas 2 have been oc-
cluded by the railing, thus have not been sampled.
This increases the difficulty of the reconstruction task.
Here, TVL
1
interpolates a shape, which corresponds
more to the ground truth than the two compared tech-
niques. The area marked by 3 is the balcony, where
only a small part of the floor has been sampled. In
such areas, both TVL
1
and SSD perform well, sig-
nificantly outperforming the Poisson approach. The
diagram in Figure 12f) shows the error distribution
of the reconstructed shapes. It is produced by re-
sampling the ground truth model and the approxi-
mated shapes with 5M points and by measuring the
minimal distance between each reconstructed sample
and a ground truth sample. The point-to-point (ptp)
distance is shown on the horizontal axis. The his-
togram height is normalized resulting in a fraction of
samples being inside a histogram bin. The further the
peak moves to the left of the diagram, the better is
the reconstruction accuracy. As also illustrated by the
Figures 12 a)-d), TVL
1
slightly outperforms SSD and
is significantly more accurate than Poisson.
5 CONCLUSION
This paper has presented a new 3D shape modelling
strategy for noisy error prone 3D data samples. Mod-
elling 3D shapes with radial basis functions has been
proposed with the choice of the most appropriate RBF
corroborated using generalized stability and approx-
imation quality assessments. The shape regression
model has been extended by non-smooth L
1
regu-
larization assuming planar areas to improve the ac-
curacy of the reconstructed shape in indoor and ur-
ban environments. Since the TVL
1
optimization task
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
302

a) Ground truth
1
2
3
0.1
0
m
b) TVL1-C
4
c) SSD
d) Poisson
e) Shape results
ptp-distance
fraction of samples
TVL1-
TVL1-
Poisson
SSD
f) Error histogram
Figure 12: Evaluation results for the proposed TVL
1
and
the compared techniques.
is computationally expensive, a low complexity opti-
mization technique has been developed. The opti-
mization process exploits the Lagrangian form of
the optimization task with an iterative over relax-
ation technique. This enables realistic datasets con-
taining several millions points to be effectively pro-
cessed. Quantitative analysis confirms that the pro-
posed method achieves superior accuracy on the syn-
thetic objects.
For future research, the presented solution will be
adapted and extended to recursive, real-time 3D map-
ping applications where environment measurements
are received as a data stream. The corresponding 3D
shape approximation model will be then able to recur-
sively modify its shape as new measurements become
available.
REFERENCES
Agoston, M. (2005). Computer Graphics and Geometric
Modelling: Implementation & Algorithms. Computer
Graphics and Geometric Modeling. Springer.
Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin,
D., and Silva, C. T. (2001). Point set surfaces. In
Proceedings of the Conference on Visualization ’01,
VIS ’01, pages 21–28, Washington, DC, USA. IEEE
Computer Society.
Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin,
D., and Silva, C. T. (2003). Computing and render-
ing point set surfaces. Visualization and Computer
Graphics, IEEE Transactions on, 9(1):3–15.
Alizadeh, F., Alizadeh, F., Goldfarb, D., and Goldfarb, D.
(2003). Second-order cone programming. Mathemat-
ical Programming, 95:3–51.
Bach, F. R., Jenatton, R., Mairal, J., and Obozinski, G.
(2012). Optimization with sparsity-inducing penal-
ties. Foundations and Trends in Machine Learning,
4(1):1–106.
Bernardini, F., Mittleman, J., Rushmeier, H., Silva, C., and
Taubin, G. (1999). The ball-pivoting algorithm for
surface reconstruction. IEEE Transactions on Visual-
ization and Computer Graphics, 5(4):349–359.
Bodenm
¨
uller, T. (2009). Streaming surface reconstruction
from real time 3D-measurements. PhD thesis, Techni-
cal University Munich.
Boyd, S., Parikh, N., Chu, E., Peleato, B., and Eckstein, J.
(2011). Distributed optimization and statistical learn-
ing via the alternating direction method of multipliers.
Found. Trends Mach. Learn., 3(1):1–122.
Bredies, K., Kunisch, K., and Pock, T. (2010). Total gene-
ralized variation. SIAM J. Img. Sci., 3(3):492–526.
Bregman, L. (1967). The relaxation method of finding
the common point of convex sets and its application
to the solution of problems in convex programming.
{USSR} Computational Mathematics and Mathemat-
ical Physics, 7(3):200 – 217.
Calakli, F. and Taubin, G. (2011). SSD: Smooth signed
TVL1ShapeApproximationfromScattered3DData
303

distance surface reconstruction. Computer Graphics
Forum, 30(7):1993–2002.
Canelhas, D. R. (2012). Scene Representation, Registration
and Object Detection in a Truncated Signed Distance
Function Representation of 3D Space. PhD thesis,
¨
Orebro University.
Canelhas, D. R., Stoyanov, T., and Lilienthal, A. J.
(2013). Sdf tracker: A parallel algorithm for on-line
pose estimation and scene reconstruction from depth
images. In Intelligent Robots and Systems (IROS),
2013 IEEE/RSJ International Conference on, pages
3671–3676. IEEE.
Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J.,
Fright, W. R., McCallum, B. C., and Evans, T. R.
(2001). Reconstruction and representation of 3d ob-
jects with radial basis functions. In Proceedings of the
28th Annual Conference on Computer Graphics and
Interactive Techniques, SIGGRAPH ’01, pages 67–
76, New York, NY, USA. ACM.
Chen, X., Lin, Q., Kim, S., Pe
˜
na, J., Carbonell, J. G.,
and Xing, E. P. (2010). An efficient proximal-
gradient method for single and multi-task regression
with structured sparsity. CoRR, abs/1005.4717.
Duchon, J. (1977). Splines minimizing rotation-invariant
semi-norms in sobolev spaces. In Schempp, W. and
Zeller, K., editors, Constructive Theory of Functions
of Several Variables, volume 571 of Lecture Notes in
Mathematics, pages 85–100. Springer Berlin Heidel-
berg.
Dykstra, R. (1982). An Algorithm for Restricted Least
Squares Regression. Technical report, mathematical
sciences. University of Missouri-Columbia, Depart-
ment of Statistics.
Edelsbrunner, H. and M
¨
ucke, E. P. (1994). Three-
dimensional alpha shapes. ACM Trans. Graph.,
13(1):43–72.
Efron, B., Hastie, T., Johnstone, I., and Tibshirani, R.
(2004). Least angle regression. Annals of Statistics,
32:407–499.
Friedman, J. H., Hastie, T., and Tibshirani, R. (2010). Reg-
ularization paths for generalized linear models via
coordinate descent. Journal of Statistical Software,
33(1):1–22.
Getreuer, P. (2012). Rudin-Osher-Fatemi Total Variation
Denoising using Split Bregman. Image Processing On
Line, 2:74–95.
Goldstein, T. and Osher, S. (2009). The split bregman
method for l1-regularized problems. SIAM J. Img.
Sci., 2(2):323–343.
Gomes, A., Voiculescu, I., Jorge, J., Wyvill, B., and
Galbraith, C. (2009). Implicit Curves and Sur-
faces: Mathematics, Data Structures and Algorithms.
Springer Publishing Company, Incorporated, 1st edi-
tion.
Guennebaud, G. and Gross, M. (2007). Algebraic point set
surfaces. ACM Trans. Graph., 26(3).
H
¨
agele, M. (2011). Wirtschaftlichkeitsanalysen neuartiger
Servicerobotik-Anwendungen und ihre Bedeutung f
¨
ur
die Robotik-Entwicklung.
Hirschm
¨
uller, H. (2011). Semi-global matching - motiva-
tion, developments and applications. In Fritsch, D.,
editor, Photogrammetric Week, pages 173–184. Wich-
mann.
Hughes, J., Foley, J., van Dam, A., and Feiner, S. (2014).
Computer Graphics: Principles and Practice. The
systems programming series. Addison-Wesley.
Kazhdan, M. and Hoppe, H. (2013). Screened poisson sur-
face reconstruction. ACM Trans. Graph., 32(3):29:1–
29:13.
Ohtake, Y., Belyaev, A., Alexa, M., Turk, G., and Seidel,
H.-P. (2003). Multi-level partition of unity implicits.
ACM Trans. Graph., 22(3):463–470.
Open Source Community (2014). Blender, open source
film production software. http://blender.org. Ac-
cessed: 2014-06-6.
Oztireli, C., Guennebaud, G., and Gross, M. (2009). Fea-
ture Preserving Point Set Surfaces based on Non-
Linear Kernel Regression. Computer Graphics Fo-
rum, 28(2):493–501.
Piegl, L. and Tiller, W. (1997). The NURBS Book. Mono-
graphs in Visual Communication. U.S. Government
Printing Office.
Rogers, D. F. (2001). Preface. In Rogers, D. F., editor,
An Introduction to NURBS, The Morgan Kaufmann
Series in Computer Graphics, pages xv – xvii. Morgan
Kaufmann, San Francisco.
Rudin, L. I., Osher, S., and Fatemi, E. (1992). Nonlinear
total variation based noise removal algorithms. Phys.
D, 60(1-4):259–268.
Saad, Y. (2003). Iterative Methods for Sparse Linear Sys-
tems. Society for Industrial and Applied Mathematics,
Philadelphia, PA, USA, 2nd edition.
Sch
¨
olkopf, B. and Smola, A. J. (2001). Learning with Ker-
nels: Support Vector Machines, Regularization, Opti-
mization, and Beyond. MIT Press, Cambridge, MA,
USA.
Tennakoon, R., Bab-Hadiashar, A., Suter, D., and Cao,
Z. (2013). Robust data modelling using thin plate
splines. In Digital Image Computing: Techniques and
Applications (DICTA), 2013 International Conference
on, pages 1–8.
Tibshirani, R. (1994). Regression shrinkage and selection
via the lasso. Journal of the Royal Statistical Society,
Series B, 58:267–288.
Wahba, G. (1990). Spline models for observational data,
volume 59 of CBMS-NSF Regional Conference Series
in Applied Mathematics. Society for Industrial and
Applied Mathematics (SIAM), Philadelphia, PA.
Wendland, H. (1995). Piecewise polynomial, positive defi-
nite and compactly supported radial functions of mini-
mal degree. Advances in Computational Mathematics,
4(1):389–396.
Wendland, H. (2004). Scattered Data Approximation. Cam-
bridge University Press.
Wolff, D. (2013). OpenGL 4 Shading Language Cookbook,
Second Edition. EBL-Schweitzer. Packt Publishing.
Zach, C., Pock, T., and Bischof, H. (2007). A globally opti-
mal algorithm for robust tv-l1 range image integration.
In Computer Vision, 2007. ICCV 2007. IEEE 11th In-
ternational Conference on, pages 1–8.
Zhao, H., Oshery, S., and Fedkiwz, R. (2001). Fast surface
reconstruction using the level set method. In In VLSM
01: Proceedings of the IEEE Workshop on Variational
and Level Set Methods.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
304
