The Gradient Product Transform for Symmetry Detection and Blood

Vessel Extraction

Christoph Dalitz, Regina Pohle-Fr

ohlich, Fabian Schmitt and Manuel Jeltsch

Institute for Pattern Recognition, Niederrhein Univerity of Applied Sciences, Reinarzstr. 49, 47805 Krefeld, Germany

Keywords:

Symmetry Detection, Image Filtering, Blood Vessels, Vesselness Filter, Angiography.

Abstract:

The “gradient product transform” is a recently proposed image ﬁlter for assigning each image point a symmetry

score based on scalar products of gradients. In this article, we show that the originally suggested method for

ﬁnding the radius of the symmetry region is unreliable, and a more robust method is presented. Moreover, we

extend the symmetry transform to rectangular symmetry regions so that it is more robust with respect to skew,

and the transform is generalised to also work with three dimensional image data. We apply the transform

to two different problems: detection of objects with rotational symmetry, and blood vessel extraction from

medical images. In an experimental comparison with other solutions for these problems, the gradient product

transform performs comparable to the best known algorithm for rotational symmetry detection, and better than

the vesselness ﬁlter for blood vessel extraction.

1 INTRODUCTION

A symmetry is a geometric transformation under

which a subset of an image is invariant. Formally,

when f (~x) is the pixel value at position ~x, then a re-

gion Ω is symmetric under the transformation σ if

f (σ(~x)) = f (~x) for all ~x ∈ Ω (1)

The class of the transformation σ deﬁnes the symme-

try type: reﬂection, rotation, or translation. In Fig-

ure 1, the symmetry region Ω is the church window

and it is invariant under reﬂections at the six yellow

axes, and also under rotations with angles α = k ·2π/6

around the intersection point of the axes. Rotations by

multiples of 2π/m form the symmetry group C

, with

the special case C

∞

denoting rotation invariance under

arbitrary angles.

A survey of symmetry detection algorithms can

be found in (Liu et al., 2010). Generally, these algo-

rithms assign each image point a “symmetry score”

that measures how suitable the point is as a symmetry

centre. The image of symmetry score values thus rep-

resents a “symmetry transform”, and symmetry points

correspond to maxima in the symmetry transform im-

age. The computation of the symmetry score depends

on the type of symmetry and is speciﬁc to each algo-

rithm.

For detecting C

(point reﬂection) symmetries in

greyscale images, Dalitz et al. have recently proposed

an algorithm that is based on scalar products of grey

value gradients at corresponding positions. Let us call

the resulting symmetry transform the gradient prod-

uct transform. In (Dalitz et al., 2013), this transform

was deﬁned based on a square shaped mask and meth-

ods were given for determining the size of the symme-

try region and for discriminating between rotational

symmetries and axial symmetries. The latter can be

useful for ﬁnding actual rotation symmetries, because

reﬂection symmetries can also show up as C

symme-

tries (see Figure 2).

The gradient product transform was reported in

(Dalitz et al., 2013) to perform comparable to or even

better than the method by Loy & Eklundh (Loy and

Figure 1: A symmetric object. The church window shows

reﬂection symmetries according to the yellow axes and a C

rotation symmetry.

177

Dalitz C., Pohle-Fröhlich R., Schmitt F. and Jeltsch M..

The Gradient Product Transform for Symmetry Detection and Blood Vessel Extraction.

DOI: 10.5220/0005234101770184

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 177-184

ISBN: 978-989-758-090-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

axis

rotation by

symmetry

Figure 2: A C

symmetry that also is a reﬂection symmetry.

Eklundh, 2006), an algorithm that performed best in

several comparative studies (Rauschert et al., 2011;

Park et al., 2008; Liu et al., 2013). Nevertheless,

there are still two shortcomings of the gradient prod-

uct transform as deﬁned by Dalitz et al., which we

address in the present article. The ﬁrst is that its def-

inition is based upon square shaped regions, which is

not appropriate for non circular point symmetric ob-

jects and which also makes the symmetry transform

very sensible to skew. We therefore generalise the

transform to work with rectangular regions and give

a recursion formula that allows for an efﬁcient com-

putation of the transform.

The other shortcoming is that the original method

for determining the size of the symmetry region is not

very robust. In (Dalitz et al., 2013), it is deﬁned as

the radius with the highest occurring symmetry score,

which worked in the experiments because the radii

used for testing were not greater than the largest sym-

metric object in each image. In this article we demon-

strate however that the symmetry score tends to in-

crease with the size of the trial region, even when

the size goes beyond the actual symmetry region. In

other words, the detected symmetry size for the origi-

nal method is generally simply the largest radius tried

out. We therefore propose a normalisation that reme-

dies this problem.

Comparative studies on symmetry detection usu-

ally discuss and evaluate symmetry transforms as

a means for locating symmetric objects within

an unsymmetrical environment (Park et al., 2008;

Rauschert et al., 2011; Liu et al., 2013), thereby only

taking the location of maxima of a symmetry trans-

form into account. From a more general viewpoint,

the symmetry transform can alternatively be consid-

ered as an image ﬁlter that transforms a greyscale im-

age into an image of symmetry scores. To demon-

strate the usefulness of such a ﬁlter, we apply the gra-

dient product transform as a preprocessing operation

to retina fundus photographs and show that blood ves-

sels can be easily extracted from this ﬁltered image.

In the preliminary study (Pohle-Fr

ohlich and Stalder,

2014), Pohle-Fr

ohlich & Stalder have demonstrated

that the gradient product transform can be useful for

blood vessel extraction in 3D medical images. In the

present article, we do a systematic evaluation of the

gradient product transform performance on the 2D

dataset of retina images by Staal et al. (Staal et al.,

2004) and compare it to the standard algorithm for

blood vessel extraction, the vesselness ﬁlter (Drech-

sler and Laura, 2010).

2 THE GRADIENT PRODUCT

TRANSFORM

The gradient product transform ﬁrst computes for

each image point ~x = (x,y) of a greyscale image and

for a range of radii ~r = (r

) a symmetry score

s(~x,~r). From these values, an “optimal” radius

R(~x) =

) is determined for each image point, and the

ﬁnal symmetry transform is then deﬁned as S(~x) =

s(~x,

R(~x)). In (Dalitz et al., 2013), only the case of

square shaped symmetry regions was considered, i.e.

= r

. Here we give formulae for the general case.

Section 2.1 describes the computation of s(~x,~r),

Section 2.2 deﬁnes a criterion for selecting

R(~x), and

in Section 2.3 we give a criterion for discriminating

between axial and actual rotational symmetries.

2.1 Symmetry Score

Although homogeneous regions comply with the

symmetry deﬁnition (1), they are of little interest for

symmetry detection, because objects are better char-

acterised by their edges. The starting point of the

symmetry score computation is thus the gradient im-

age

G(~x), which can be computed from a greyscale

image, e.g., with a Sobel ﬁlter.The symmetry score

formula is based on two observations:

• under point reﬂection symmetry, the mirrored gra-

dient

is anti-parallel to the gradient

G (see Fig-

ure 3)

• the scalar product h

i is minimal for

= −

The symmetry score for the rectangle with circum-

radius ~r = (r

) around the centre point ~x = (x,y),

i.e., the rectangle with upper left~x −~r and lower right

x + d

= −

→

→→

G ′

→

x − d

→

Figure 3: Effect of a point reﬂection at ~x on the gradient.

The gradient

G at ~x +

d is mapped onto the gradient

−

G at ~x −

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

178

~x +~r, is therefore deﬁned as

s(~x,~r) = −

∑

G(d

,0),

G(−d

,0)

−

∑

=−r

G(d

G(−d

,−d

)

(2)

where

G(d

) denotes the gradient at position (x +

,y + d

). The sum is split up so that each point pair

only occurs once, and the minus sign is added for con-

venience so that a higher symmetry corresponds to a

higher score value, not vice versa. As the size of the

symmetry region is not known in advance, the score

(2) must be computed for all radii 1 ≤ r

≤ r

max

All scores s(~x,~r) can be computed in a single run over

the symmetry region with the following recursion for-

mula for r

> 1:



~x,(r

)



= s



~x,(r

− 1,r

)



(3)



~x,(r

− 1)



−s



~x,(r

− 1,r

− 1)



−h

G(r

G(−r

,−r

−h

G(r

,−r

G(−r

The computation of all scores up to a radius r

max

thus only requires O(r

max

) additions, not O(r

max

) that

would be required by a na

ıve application of Eq. (2).

To generalise Eq. (2) to more than two dimensions, it

is more convenient to notate the formula in a compact

vector notation:

s(~x,~r) = −

∑

d∈Ω(−~r,~r)

d6=

d),

G(−

(4)

where

d) denotes the greyscale gradient at position

~x +

d, and Ω(−~r,~r) denotes the region of the rectangle

or cuboid with corners −~r and~r. The factor 1/2 com-

pensates for the fact that each pair of corresponding

mirror points occurs twice in the sum. Eq. (4) holds

for any dimension.

2.2 Symmetry Size

When the symmetry score (2) is computed for a range

of circumradii ~r, the question arises which of these

radii represents the size of the symmetry region. In

(Dalitz et al., 2013), Dalitz et al. suggested to simply

take the radius with the highest score, which would be

for our generalised case of rectangular regions

R = arg

max{s(~x,~r) | max(r

) ≤ r

max

} (5)

−α

(r/r )

s(r) / s(r )

r / r

0.2

0.4

0.6

0.8

1.2

1.4

0 0.5 1 1.5 2

α = 0.0

α = 0.5

α = 1.0

Figure 4: Symmetry score as a function of the radius. On

average, the symmetry score s(r) increases with r even

when r becomes larger than the actual size r

of the sym-

metric object. Division by a factor r

can compensate for

this effect.

The problem with this deﬁnition is that it tends to pick

a radius quite close to r

max

, even when the actual sym-

metric object is much smaller. To understand this phe-

nomenon, we have computed the symmetry score as

a function of the radius r with square shaped regions

= r

= r) for all ground truth symmetry points in

the data set (Dalitz et al., 2013). To make the mea-

surements comparable, we have normalised all radii

with the ground truth radius r

, and all scores with

the score S(r

). As can be seen in Figure 4 (curve for

α = 0), the score increases steeply for r ≤ r

, as ex-

pected, but still increases as r becomes larger than r

albeit not as steep. This is simply due to the fact that

the number of summands in (2) grows with r so that

random ﬂuctuations can increase the sum.

To remedy this problem, the symmetry score

needs to be normalised by a factor that depends on~r.

Even though the number of summands in (2) is pro-

portional to the area of the symmetry region, which is

· r

, only scalar products with large gradients will

contribute signiﬁcantly to the sum. As the gradient

is large for edges, and the number of edge points is

proportional to the surface of the symmetry region,

it seems natural to normalise with r

+ r

. As can

be seen from the curve for α = 1.0 in Figure 4, this

indeed leads on average to a maximum score at the

actual symmetry size, but it also has the side effects

that the score values of small symmetry regions are

increased.

To control the trade off between these two effects,

we normalise with (r

)

, where α = 0.5 is a com-

promise between both effects. The effect of the choice

of α on the symmetry radius detection can be seen in

Figure 5, where we have set r

max

to the size of the im-

age. We therefore deﬁne the optimum circumradius

R = (R

) and the resulting symmetry transform

value S at position~x as

TheGradientProductTransformforSymmetryDetectionandBloodVesselExtraction

179

Figure 5: Impact of α on the symmetry radius determina-

tion. Symmetry circumradius around the highest symmetry

score in the image with α = 0 (yellow), α = 0.5 (green),

and α = 1.0 (red).

R(~x) = arg

max



s(~x,~r)

+ r

)



max(r

) ≤ r

max



and S(~x) =

s(~x,

R(~x))

(~x) + R

(~x))

(6)

For more than two dimensions, the normalisation de-

nominator (r

+ r

)

in Eq. (6) must be replaced with

(

∑

i=1

for the circumradius~r = (r

,...,r

2.3 Symmetry Type

As already pointed out in the introduction (see Figure

2 above), some axial symmetries can also be C

sym-

metries. A practical example can be seen in Figure 6:

the highest local maximum in the symmetry transform

corresponds to the region highlighted in red, which

has both a C

and an axial symmetry, while the second

highest local maximum in the symmetry transform

corresponds to the C

∞

symmetry highlighted in green.

In (Dalitz et al., 2013), a simple threshold based dis-

crimination between these two types of symmetry was

proposed, based upon the edge directedness in the

neighbourhood of the symmetry centre (the threshold

was set to 0.27).

In this section, we investigate this discrimination

in more detail with a quadratic discriminant analysis.

As can be seen from the symmetry transform image

in Figure 6, for axial symmetries the entire symme-

try axis tends to obtain high symmetry scores, while

for pure rotational symmetries the symmetry score de-

cays with the distance to the symmetry centre inde-

pendent from the direction. We therefore compute the

following features for a candidate symmetry centre ~x,

i.e., for a local maximum of the symmetry score S(~x):

Edge Directedness. This feature is based on the angle

histogram of the gradients of the symmetry trans-

Figure 6: Symmetry transform of a sample image. The two

highest symmetry scores and the corresponding circumradii

according to Eq. (6) with α = 0.5.

form in a k × k window centred at ~x. We compute

the gradients by applying a Sobel ﬁlter to the sym-

metry transform and build a weighted histogram

with 16 bins of the gradient angles. Each angle is

weighted in the histogram with the corresponding

absolute value of the gradient. The edge directed-

ness is then deﬁned as the highest occurring fre-

quency in this histogram, and it should be higher

for axial symmetries.

Skeleton Size. Starting from~x, we follow the skeleton

until the score falls below a percentage p of S(~x).

The feature is then the ratio between the skeleton

length and the size

h~r,~ri of the symmetry re-

gion, where~r is the circumradius of the symmetry

region. It should be higher for axial symmetries.

Antiparallel Directions. This feature is based on the

gradient of the original greyscale image. We com-

pute the direction histogram with eight bins of all

gradients in a window with the radius min{R

}

according to Eq. (6). Only those gradients are

taken into account for which the mirrored gradi-

ent is “antiparallel”, i.e. the cosine of the angles

between the gradients is less than -0.975. The fea-

ture is the highest relative frequency in the direc-

tion histogram. The value for “antiparallel direc-

tions” should be lower for rotational symmetries.

Covariance Eigenratio. For the points in a k ×k win-

dow around (x,y) in the symmetry transform im-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

180

Scatter Plot Matrix

edge_dir

0.4

0.5

0.6

0.7

0.4 0.5 0.6 0.7

0.1

0.2

0.3

0.4

0.1 0.2 0.3 0.4

skel_size

0.6

0.8

1.0

0.6 0.8 1.0

0.0

0.2

0.4

0.0 0.2 0.4

anti_par

0.4

0.5

0.4 0.5

0.2

0.3

0.2 0.3

cov_ratio

0.6

0.8

1.0

0.6 0.8 1.0

0.0

0.2

0.4

0.0 0.2 0.4

Figure 7: Scatterplots for the four features for symmetry

type discrimination. The blue points belong to axial sym-

metries, the magenta points to rotational symmetries.

age, we compute the covariance matrix K as

K =

k/2

∑

dx=−k/2

k/2

∑

dy=−k/2

S(x + dx, y + dy) (7)



dx dx dx dy

dy dx dy dy



where S(x,y) is the symmetry transform value at

(x,y), and the normalisation factor N is the sum

over all symmetry values in the window. The

eigenvalues of K indicate how strongly the val-

ues spread in the direction of the corresponding

eigenvector. Consequently, the ratio between the

smaller and the larger eigenvalue should be higher

for rotational symmetry.

The data set (Dalitz et al., 2013) contains lists of

ground truth points that are labelled as either axial or

rotational symmetry centres, which provides a test set

for this classiﬁcation tasks. The scatterplots in Figure

7 actually reveal the tendencies in the above descrip-

tions, but there is considerable overlap between the

classes. Nevertheless, the scatterplots indicate that it

is better to use more than one feature, and we there-

fore applied a quadratic discriminant analysis as im-

plemented in the MASS package of the R statistical

language

, which decides for the class with the largest

discriminant function

(~x) = −w

− k(~x −~µ

) ·W

(8)

where the index i ∈ {a,r} denotes the class (axial or

rotational) and ~x is the row vector of the four features

http://www.r-project.org

in the same order as in the list above. The parameters

~µ

, w

and W

were evaluated by the R function qda as

= −15.03338 w

= −21.49041 (9)

~µ

= (0.4334,0.4975, 0.4417,0.4352)

~µ

= (0.1859,0.0654, 0.2302,0.7136)







−9.3921 3.1451 7.8727 0.8677

0 −2.4364 0.3522 0.1780

0 0 −18.5275 3.1907

0 0 0 4.3365













14.3116 −6.1912 15.5453 −6.7814

0 20.3183 0.3754 −0.9648

0 0 −20.5954 −3.8730

0 0 0 −7.7489







In our experiments in Section 3.1, this quadratic

discrimination rule improved the recognition rates for

rotational symmetries by about 8% compared to the

simple decision rule based on the edge directedness

alone.

3 EXPERIMENTAL RESULTS

We have evaluated the usefulness of the gradient

product transform and compared it to other state-of-

the-art algorithms for two use cases: detection of ro-

tational objects in real world images, and extracting

the blood vessel skeleton from two-dimensional retina

fundus photographs. For the ﬁrst problem, we have

chosen the algorithm by Loy & Eklundh (Loy and

Eklundh, 2006) as a reference, because it performed

best in different comparison studies (Rauschert et al.,

2011; Park et al., 2008; Liu et al., 2013). For the sec-

ond problem, we have chosen the vesselness ﬁlter as

a reference algorithm, because it is a widely utilised

general purpose algorithm for blood vessel extrac-

tion. In the comparative study (Drechsler and Laura,

2010), Drechsler et al. demonstrated that each of the

three vesselness ﬁlter variants (Frangi et al., 1998;

Sato et al., 1998; Erdt et al., 2008) has its strengths

and weaknesses. In our experiments, we have imple-

mented the ﬁlter by Frangi et al., because the retina

images were two-dimensional, and the ﬁlter by Frangi

et al. is the only vesselness ﬁlter that can also be ap-

plied to 2D images in a straightforward way.

3.1 Rotational Symmetry Detection

To evaluate the detection of rotational symmetric ob-

jects, we have used the dataset that was used in the

study (Dalitz et al., 2013), and that is freely available

on the Internet

. This dataset consists of 159 images

http://informatik.hsnr.de/∼dalitz/data/visapp13/

TheGradientProductTransformforSymmetryDetectionandBloodVesselExtraction

181

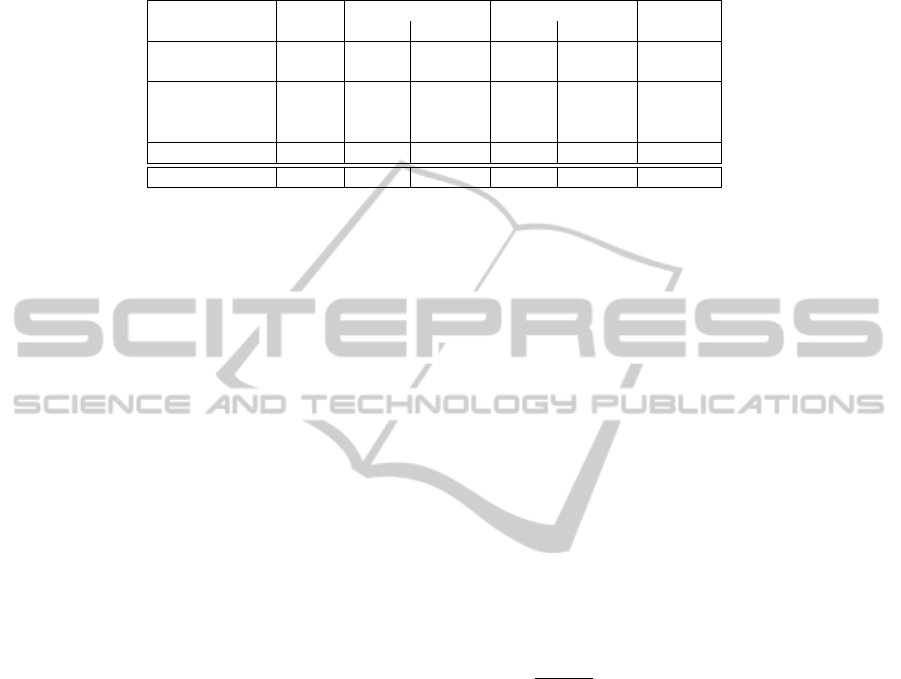
Table 1: Effect of the normalisation with α and the extension to nonsquare symmetry regions on the recognition rates for

symmetric objects in the test set (Dalitz et al., 2013). For comparison, the results for the reference algorithm by Loy &

Eklundh (Loy and Eklundh, 2006) are given. The last row gives the average area precision p

according to Eq. (10) for the

correctly detected objects.

square rectangular Loy &

Count α = 0 α = 0.5 α = 0 α = 0.5 Eklundh

Detail 83 0.58 0.60 0.59 0.58 0.37

Context 76 0.16 0.30 0.22 0.32 0.37

Front 43 0.51 0.63 0.56 0.53 0.70

Light skew 57 0.39 0.51 0.46 0.53 0.39

Strong skew 59 0.27 0.29 0.27 0.32 0.12

Total 159 0.38 0.46 0.42 0.45 0.37

Area precision 0.39 0.70 0.37 0.80

of size 600 ×400, showing 27 different subjects. Each

subject is shown in different perspectives and both in

context and in detail. This allowed us to investigate

how an algorithm performs under skew and contex-

tual noise.

For each image, we have computed all local max-

ima of the gradient product transform (r

max

= 300,

i.e. the maximum possible radius) and, among these,

searched for the highest value that was classiﬁed as

“rotational” by the quadratic discriminant analysis de-

scribed in Section 2.3. The algorithm took in total

about 3.6 sec per image on an Intel i7-4770 CPU

3.40GHz. When the position of this maximum had

a distance less than 10 pixels from a ground truth

symmetry point, we considered a symmetry to be cor-

rectly detected, otherwise it was an error. The result-

ing recognition rates are shown in Table 1. Compared

to the results in (Dalitz et al., 2013), which only used

no normalisation (α = 0) and square shaped regions

= r

), the recognition rates in the corresponding

column are lower. This is because in the experiments

of (Dalitz et al., 2013), r

max

was set to the largest

ground truth symmetry radius for each image, thereby

introducing a priori bias, especially as for α = 0 the

symmetry radius tends to be selected as r

max

The recognition rates in Table 1 show that the nor-

malisation of the symmetry score with (r

)

0.5

(see

the columns for α = 0.5) signiﬁcantly improves the

symmetry detection for the images in the “context”

category, but has little effect for the “detail” category.

This is because for the context images, the radii of

the symmetry regions are typically much smaller than

max

, and are thus less likely to be found without nor-

malisation (α = 0). The detail images on the other

hand are mostly ﬁlled out by the symmetric object so

that the correct symmetry radius is close to r

max

A comparison of the recognition rates for square

shaped regions versus rectangular regions shows that

the extension to rectangular regions indeed improves

symmetry detection for skewed symmetries, indepen-

dent of the choice for α. For unskewed symmetries

in the category “front” which actually have a circular

symmetry region, the recognition rate for rectangular

regions was however 10% smaller for α = 0.5, due to

the larger search space for the optimum circumradius

). Depending on the application, it is thus rec-

ommendable to restrict the ratio r

to a maximum

amount of permitted skew.

The recognition rates only measure whether the

location of a symmetry centre was correctly found,

but not whether the entire symmetry region has been

correctly detected. We have therefore additionally

measured the area precision of the detected circum-

radius for the correctly detected symmetries. Let G

be the smallest rectangle enclosing the ground truth

symmetry region, and T be the detected symmetry re-

gion with corners ~x ±

R(~x). Then we deﬁned the area

precision p

|T ∩ G|

|T ∪ G|

with |X| = area of X (10)

As can be concluded from the last row in Table 1, both

the normalisation and the generalisation to rectangu-

lar regions clearly improve the accuracy of the shapes

of the detected symmetry regions.

Compared to the algorithm by Loy & Eklundh,

the gradient product transform is unaffected by light

skew, but is less robust with respect to contextual

noise. For the algorithm by Loy & Eklundh, it is just

the other way round.

3.2 Blood Vessel Extraction

The problem of blood vessel extraction occurs for

many types of medical images, e.g. for angiographs,

fundus photographs, or MRT-TOF datasets. For blood

vessel extraction from two-dimensional retina fundus

photographs, Staal et al. have created an evaluation

dataset known as the DRIVE database (“Digital Reti-

nal Images for Vessel Extraction”) (Staal et al., 2004).

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

182

In consists of 40 colour images, divided into 20 train-

ing and 20 test images, with ground truth data manu-

ally extracted by medical experts (see Figure 8).

From the colour images, we have used the green

channel as input to both our symmetry transform and

the vesselness ﬁlter, because this channel had the

highest contrast. It should be noted that Shahbeig

recently suggested sophisticated preprocessing oper-

ations on these particular images which strongly en-

hance the visibility of the blood vessels (Shahbeig,

2013). As we were less concerned with the speciﬁc

problem of retina photographs, but wanted to evaluate

the vessel extraction on typical medical images, we

restricted ourselves to a Gaussian blur with window

size k = 3 and variance σ

= 1.0 as the only prepro-

cessing operation on the green channel images; this

preprocessing operation was only applied before the

symmetry transform, but not before the vesselness ﬁl-

ter because the latter does a Gaussian blurring any-

way.

When applying the gradient product transform to

blood vessel extraction, there are two issues:

1) Depending on the imaging technique, blood ves-

sels are either darker or lighter than the surround-

ing tissue, but the gradient product transform in-

variably detects symmetries in both dark and light

objects.

2) The gradient product transform results in a ﬂoat

image of symmetry scores and not in a skeleton

image. The same holds for the vesselness ﬁlter.

To solve the the ﬁrst issue, we have modiﬁed the

symmetry score from Eq. (4) to

s(~x,~r) = −

∑

d∈Ω(−~r,~r)

d6=

d),

G(−

(11)

× H



E

where H denotes Heavyside’s step function (zero for

negative arguments, and one for positive arguments),

and the sign in its arguments controls which type of

objects are detected. For dark vessels, the plus sign

should be used because it has the effect that only gra-

Figure 8: Sample image from the DRIVE dataset and its

corresponding ground truth.

Figure 9: Impact of Heavyside’s step function on the gra-

dient product transform. The left image is the result of

the original gradient product transform, and the right image

the result after the modiﬁcation (11) (the ﬂoat images have

been converted to greyscale and the greyscale histogram

was equalised).

excess

missed

1 −

gradient product transform

vesselness filter

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

0.4

0.5

0.6

0.7

0.8

0.9

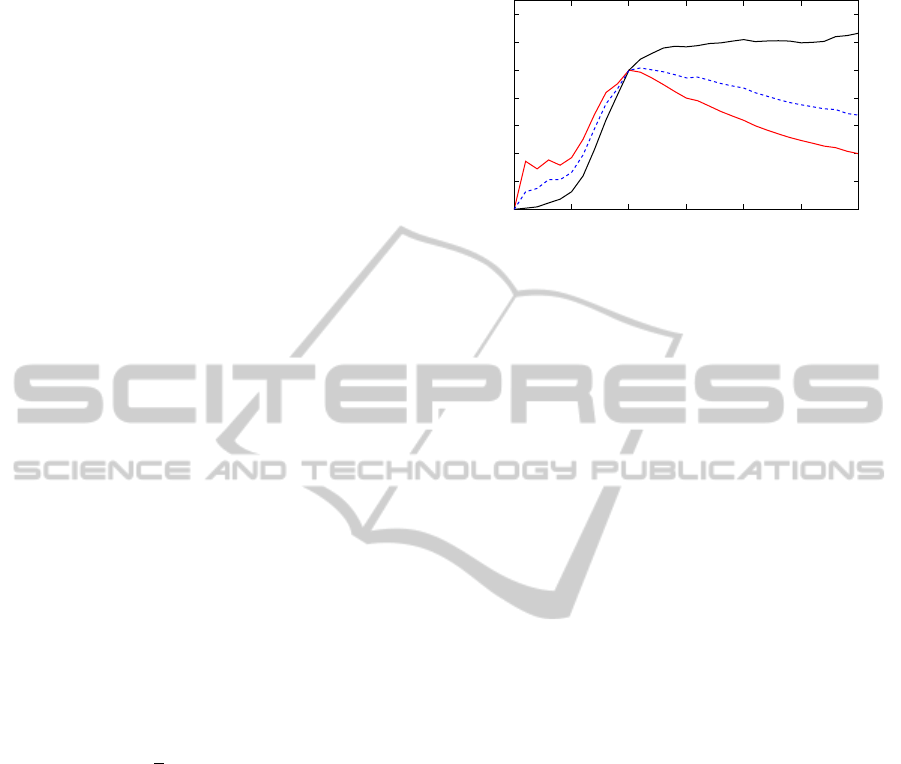
Figure 10: ROC-curves for blood vessel extraction on the

DRIVE dataset. p

missed

and p

excess

have been averaged over

all of the 40 images. Different points on the same curve

correspond to different threshold values.

dients pointing outwards contribute to the sum. Fig-

ure 9 shows the impact of this modiﬁcation.

Concerning the second issue, we have binarised

the ﬂoat image with a global threshold and extracted

the medial axis transform skeleton from the binary

image with the algorithm by Haralick & Shapiro (Har-

alick and Shapiro, 1992), as implemented in the Gam-

era framework

. To compare a resulting skeleton T

with the skeleton S of the corresponding ground truth

image, we computed the percentage of missed and ex-

cess pixels as

missed

= |S \ (T ⊕ H)|

|S| (12)

excess

= |T \ (S ⊕ H)|

|T |

where “⊕H” denotes morphological dilation with a

3 × 3 structuring element H and |X| denotes the num-

ber of pixels in X.

There is a trade-off between the values for p

missed

and p

excess

, depending on the threshold value: for a

lower threshold, the skeleton includes more pixels and

http://gamera.sf.net/

TheGradientProductTransformforSymmetryDetectionandBloodVesselExtraction

183

missed

is smaller, but p

excess

is greater. To compare

the performances of gradient product transform and

vesselness ﬁlter, we therefore tried a range of thresh-

olds and computed the receiver operating character-

istics (ROC), which is shown in Figure 10. For the

gradient product transform, we have chosen r

max

= 3

and α = 0.5. For the vesselness ﬁlter, we have tried

all values σ ∈ {0.1,0.2,...,3.0} and selected for each

pixel the largest vesselness score.

From Figure 10, we conclude that the gradient im-

age transform performs better than the vesselness ﬁl-

ter for blood vessel extraction, because it yields more

correctly detected vessels for the same rate of false

positives. Note that the ROC curve for the vesselness

ﬁlter is shorter, because the threshold cannot become

less than zero. The same excess rate as with the ves-

selness ﬁlter for threshold zero was obtained with the

gradient product transform for a threshold set to half

the mean positive symmetry score.

4 CONCLUSIONS

The symmetry score normalisation for the gradient

product transform, as suggested in this article, clearly

improves the detection of the size of the symme-

try region and removes the necessity of an approx-

imate a priori guess of the maximum circumradius

max

. For the power α in the normalisation, we rec-

ommend α = 0.5. The generalisation to rectangular

regions makes the gradient product transform more

robust with respect to light skew.

Moreover, we have demonstrated that the gradi-

ent product transform can be useful as an image ﬁlter

beyond the narrow problem of symmetry detection.

An additional factor in the symmetry transform that

suppresses symmetry responses from light (or dark)

regions makes the gradient product transform well

suited for blood vessel extraction from medical im-

ages. To this end, it performs better than the ves-

selness ﬁlter, and can thus be a replacement for this

standard algorithm for blood vessel extraction. As a

global threshold for the symmetry score of blood ves-

sels, 0.5 times the mean positive score worked well in

our examples.

To enable others to easily build upon our results,

we make the source code of our new generalised sym-

metry transform and for the blood vessel extraction

freely available on our website

smallhttp://informatik.hsnr.de/∼dalitz/data/visapp13/

REFERENCES

Dalitz, C., Pohle-Fr

ohlich, R., and Bolten, T. (2013). De-

tection of symmetry points in images. In International

Conference on Computer Vision Theory and Applica-

tions (VISAPP), pages 577–585.

Drechsler, K. and Laura, C. (2010). Comparison of vessel-

ness functions for multiscale analysis of the liver vas-

culature. In Information Technology and Applications

in Biomedicine (ITAB), 2010 10th IEEE International

Conference on, pages 1–5.

Erdt, M., Raspe, M., and S

uhling, M. (2008). Automatic

hepatic vessel segmentation using graphics hardware.

In Medical Imaging and Augmented Reality, 4th Inter-

national Workshop, MIAR 2008, pages 403–412.

Frangi, A., Niessen, W., Vincken, K., and Viergever, M.

(1998). Multiscale vessel enhancement ﬁltering. In

Medical Image Computing and Computer-Assisted In-

terventation MICCAI98, pages 130–137.

Haralick, R. M. and Shapiro, L. G. (1992). Computer and

Robot Vision, volume 1. Addison-Wesley, Reading,

MA.

Liu, J., Slota, G., Zheng, G., Wu, Z., Park, M., Lee, S.,

Rauschert, I., and Liu, Y. (2013). Symmetry detection

from real world images competition 2013: Summary

and results. In IEEE Conference on Computer Vision

and Pattern Recognition (CVPR).

Liu, Y., Hel-Or, H., Kaplan, C., and Gool, L. V. (2010).

Computational symmetry in computer vision and

computer graphics. Foundations and Trends in Com-

puter Graphics and Vision, 5:1–195.

Loy, G. and Eklundh, J. (2006). Detecting symmetry and

symmetric constellations of features. In European

Conference on Computer Vision (ECCV), pages 508–

521.

Park, M., Lee, S., Chen, P., Kashyap, S., Butt, A., and Liu,

Y. (2008). Performance evaluation of state-of-the-art

discrete symmetry detection algorithms. In IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 1–8.

Pohle-Fr

ohlich, R. and Stalder, D. (2014). 3D-

Symmetrietransformation zur Gef

aßsegmentierung in

MRT-TOF-Daten. In Bildverarbeitung fr die Medizin

2014, pages 144–149.

Rauschert, I., Brockelhurst, K., Liu, J., Kashyap, S., and

Liu, Y. (2011). Workshop on symmetry detection from

real world images - a summary. In IEEE Conference

on Computer Vision and Pattern Recognition (CVPR).

Sato, Y., Nakajima, S., Shiraga, N., Atsumi, H., Yoshida, S.,

Koller, T., Gerig, G., and Kikinis, R. (1998). Three-

dimensional multi-scale line ﬁlter for segmentation

and visualization of curvilinear structures in medical

images. Medical Image Analysis, 2:143168.

Shahbeig, S. (2013). Automatic and quick blood vessels ex-

traction algorithm in retinal images. Image Process-

ing, IET, 7:392–400.

Staal, J., Abramoff, M., Niemeijer, M., Viergever, M., and

van Ginneken, B. (2004). Ridge-based vessel segmen-

tation in color images of the retina. Medical Imaging,

IEEE Transactions on, 23:501–509.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

184