Metric Learning in Dimensionality Reduction

Alexander Schulz and Barbara Hammer

CITEC Centre of Excellence, Bielefeld University, Bielefeld, Germany

Keywords:

Dimensionality Reduction, Metric Learning, Interpretability, Data Visualisation.

Abstract:

The emerging big dimensionality in digital domains causes the need of powerful non-linear dimensionality

reduction techniques for a rapid and intuitive visual data access. While a couple of powerful non-linear

dimensionality reduction tools have been proposed in the last years, their applicability is limited in practice:

since a non-linear projection is no longer characterised by semantically meaningful data dimensions, the visual

display provides only very limited interpretability which goes beyond mere neighbourhood relationships and,

hence, interactive data analysis and further expert insight are hindered. In this contribution, we propose to

enhance non-linear dimensionality reduction techniques by a metric learning framework. This allows us to

quantify the relevance of single data dimensions and their correlation with respect to the given visual display;

on the one side, this explains its most relevant factors; on the other side, it opens the way towards an interactive

data analysis by changing the data representation based on the learned metric from the visual display.

1 INTRODUCTION

Digitally available data sets are ever getting bigger

as concerns its size, complexity, and dimensionality.

Big data has been proclaimed as one of today’s major

challenges in the digital society (Khalil, 2012; Com-

mittee on the Analysis of Massive Data et al., 2013),

and computational intelligence and machine learn-

ing techniques offer a fundamental approach how to

tackle a few of the involved problems (Zhai et al.,

2014; Jin and Hammer, 2014; Hammer et al., 2014).

In almost all settings, however, data analysis is not

fully automated, but the human has to decide on the

suitability of the used techniques, often in an inter-

active way. Hence it is vital to establish an intuitive

access to digital data and the possible outcomes of al-

gorithmic steps for the practitioner. Since decades,

visual data inspection offers one premier interface in

this setting, since it relies on one of human’s most

powerful senses and his astonishing cognitive capa-

bilities of instantaneous visual grouping and feature

detection (Simoff et al., 2008; Ward et al., 2010).

In this contribution, we deal with a popular set-

ting, the availability of a large number of vectorial

data points which characterise some entities (such as

measurement vectors, customer characteristics, pa-

tients, etc.). Scatter plots offer one of the most promi-

nent technique to visually inspect such data: here,

data are displayed such that their neighbourhood re-

lationship can directly be observed, and phenomena

such as clusters, complex grouping, or outliers can

easily be observed. Scatter plots are directly avail-

able for two or three dimensional data; for higher di-

mensionality, scatter matrices or tour methods have

been proposed (Simoff et al., 2008). However, their

applicability is limited for higher data dimensional-

ity, since not all information available in the different

dimensions and their correlation can easily be inte-

grated based on these simple methods.

In this context, dimensionality reduction plays a

major role, referring to the task to map high dimen-

sional vectors to low dimensional counterparts such

that as much information as possible is preserved.

One very common classical dimensionality reduction

method is offered by principal component analysis

(PCA), which constitutes the by far most popular

data visualisation technique in diverse application do-

mains (Biehl et al., 2011). However, being a linear

technique, it is severely restricted as concerns its ca-

pability to capture non-linear structures and cluster-

ing effects. In recent years, a huge variety of non-

linear dimensionality reduction techniques has been

proposed, see e.g. the overviews (Bunte et al., 2012a;

Lee and Verleysen, 2007; van der Maaten and Hin-

ton, 2008; Venna et al., 2010; Gisbrecht and Ham-

mer, 2014). Many techniques can be accompanied by

guarantees that they are capable of extracting the true,

possibly non-linear underlyingdata manifold (Roweis

and Saul, 2000; Tenenbaum et al., 2000; Gisbrecht

and Hammer, 2014); however, these techniques are

232

Schulz A. and Hammer B..

Metric Learning in Dimensionality Reduction.

DOI: 10.5220/0005200802320239

In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 232-239

ISBN: 978-989-758-076-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

not well suited to visualise data provided the under-

lying manifold structure cannot be preserved in only

two dimensions due to a higher intrinsic data dimen-

sionality (van der Maaten et al., 2009). A few pow-

erful alternatives rely on the notion of neighbourhood

structures, with the neighbourhoodretrieval visualiser

(NeRV), for example, explicitly realising an infor-

mation retrieval perspective, and allowing a suitable

compromise of the amount of information which is

preserved in the visualization (van der Maaten and

Hinton, 2008; Venna et al., 2010). These techniques

provide excellent results in application scenarios, and

they mirror what is currently accepted as state of the

art as a suitable cost function of non-parametric di-

mensionality reduction techniques (Lee and Verley-

sen, 2010; Venna et al., 2010). In this contribution, we

will mostly be concerned with NeRV as theoretically

well-founded method and one of the most powerful

non-linear data visualisation techniques available to-

day. Quite a few extensions of NeRV, or the very

similar, earlier technique t-SNE proposed in (van der

Maaten and Hinton, 2008) exist to cope with the prob-

lems of efﬁcient implementation, integration of prior

knowledge, an extension of the non-parametric tech-

nique to an explicit mapping prescription, or exten-

sions to alternative cost measures (Yang et al., 2013;

Gisbrecht et al., 2014; Hammer et al., 2013; Lee et al.,

2013).

One severe problem of techniques such as t-SNE

and NeRV lies in the fact that they are non-parametric

non-linear techniques for which the obtained visual

data display, unlike linear counterparts such as PCA,

cannot easily be linked to semantically meaningful

information: the two-dimensional projection coordi-

nates have no direct meaning and they are not linked

to feature dimensions of the data, unlike linear pro-

jections such as PCA, where the projection axes can

be linked to the original data dimensions. For non-

parametric projections the relative location of data

points is the only relevant information preserved in

the mapping. As a consequence, it is not easy to judge

which data dimensions are particularly important for

the visual display, and which correlations of the data

dimensions contribute to the mapping. Since data vi-

sualisation is an unsupervisedand inherently ill-posed

task, this fact leads to a severe risk of interpreting the

visual display in a wrong way, if its interpretation is

possible at all (Vellido et al., 2012; R¨uping, 2006).

Further, an interactive manipulation of the data by

means of the visual display is not easily possible.

Recently, a few approaches have been proposed

which try to overcome this gap and which accompany

visualisation techniques with methods to more easily

interpret the display and manipulate the data repre-

sentation based thereon (Brown et al., 2012; Endert

et al., 2012; Peltonen et al., 2013). These techniques

propose to change the data metrics based on a given

visual display, whereby different techniques are in-

volved, ranging from heuristic model updates up to

Bayesian learning of the data metric. In this contribu-

tion, we will follow these ﬁrst steps which change the

metric of the data based on a given visual display; by

incorporating recent insights from the ﬁelds of met-

ric learning in supervised machine learning, we will

arrive at a very simple and intuitive metric adaptation

scheme which offers insight into the visual display as

well as ways to manipulate the data representation ac-

cordingly.

Metric learning constitutes a very powerful

scheme well-known in machine learning, and a va-

riety of techniques has been proposed in the context

of supervised learning, see e.g. (Bellet et al., 2013;

Bunte et al., 2012b; Goldberger et al., 2004; Mokbel

et al., 2014). Mostly, a global or local Mahalanobis

distance is adapted in these settings such that the

underlying goal (usually classiﬁcation) is improved

as much as possible. Besides an improved model

accuracy, these techniques provide auxiliary insight

into the task by providing a relevance weighting of

the data dimensions indicating the contribution of the

data dimensions to the task at hand, and, by means

of the linear transformation underlying the quadratic

form, a new data representation which can even di-

rectly be used to inspect the data in some cases.

Here, we will transfer a particularly elegant metric

learning scheme to the ﬁeld of unsupervised dimen-

sionality reduction (Biehl et al., 2009). This scheme

will allow us to learn a global quadratic form which

mirrors the neighbourhood relationships as provided

by the visual display. The metric allows a direct

interpretation of the relevance of the feature dimen-

sions for the given mapping; further, since it can be

linked to a linear data transformation, it enables a

change of the data representation based on the visual

display, hence it allows us to impose external infor-

mation on the data in a very simple form. We will

demonstrate this latter principle by referring to dis-

criminative dimensionality reduction settings. First

steps along this line have been presented in the recent

publication (Schulz et al., 2014). Unlike this work,

we will deal with a general quadratic form instead of

a simple diagonal scaling only. Further, we focus on a

parametric metric adaptation based on a differentiable

cost function rather than referring to feature selection

techniques based on suitable evaluation schemes for

dimensionality reduction. This focus has the advan-

tage that the relevance and correlations of the given

feature dimensions can be judged simultaneously, and

MetricLearninginDimensionalityReduction

233

that the resulting transformation provides an alterna-

tive, linear data transformation which approximates

the observed display.

Now we will explain the neighbourhood retrieval

visualiser and its relation to a quantitative evalua-

tion of dimensionality reduction techniques. After-

wards, we introduce a simple and powerful metric

learning scheme based on NeRV, which enables the

efﬁcient learning of relevance matrices by a superpo-

sition of a cost optimisation and suitable regularisa-

tion. Thereby, the scheme can be used independently

of the technique which is underlying the visual dis-

play. We demonstrate the suitability and efﬁciency of

the approach in three benchmarks: an artiﬁcial sce-

nario with known ground truth, and two real life med-

ical data set, where we investigate the suitability of

the induced transformation of the given data.

2 NEIGHBORHOOD RETRIEVAL

OPTIMIZER

Given a data set X = [x

,...,x

], non-parametric di-

mensionality reduction maps data points x

∈ R

projections y

∈ R

with Y = [y

,...,y

] such that

as much structure as possible is preserved. Tech-

niques differ in the way how this is formalised, see

e.g. (Bunte et al., 2012a) for a unifying presentation

of popular dimensionality reduction schemes. Lin-

ear methods such as PCA offer an explicit mapping

= w

while many non-linear dimensionality re-

duction schemes are non-parametric. We will exem-

plarily consider NeRV (Venna et al., 2010) which, as

an objective, can be linked to neighbourhood preser-

vation in an information theoretic sense.

Assume d refers to the distance in the data space

X. We deﬁne

j|i

exp(−d(x

)

/(σ

)

∑

k6=i

exp(−d(x

)

/(σ

)

(1)

as the probability of two points being neighbour in the

data space, and

j|i

exp(−ky

− y

/(σ

)

∑

k6=i

exp(−ky

− y

/(σ

)

(2)

as the probability of two projections being neighbour

in the projection space. Thereby, the standard devi-

ation σ

in the data space is chosen such that a ﬁxed

effective numberof neighbours k (with default k = 10)

is reached and then the standard deviation σ

is set to

the same value. NeRV optimises the costs

NeRV

(X,Y) =

∑

j6=i

j|i

log

j|i

+ (1− γ)

∑

j6=i

j|i

log

j|i

(3)

corresponding to the deviation of the two probability

distributions. γ ∈ [0,1] weights the relevance of ob-

taining a good recall, corresponding to the ﬁrst sum-

mand, and a good precision, corresponding to the sec-

ond summand; per default, a compromise γ = 0.5 is

chosen. Optimisation is commonly done by a stochas-

tic or conjugate gradient descent. There exist very

similar alternative methods such as t-NeRV, which

uses the student-t distribution instead of Gaussians for

the low dimensional embedding, to better prevent the

so-called crowding problem, or (t-)SNE, which op-

timises only one summand of these costs (van der

Maaten et al., 2009).

Interestingly, the NeRV costs can be interpreted

as a smoothed version of the crisp costs which eval-

uate the degree of neighbourhood preservation for a

given DR display, as formalised in the frame of the

co-ranking framework as proposed in (Lee and Ver-

leysen, 2009), see also (Venna et al., 2010). Assume

a ﬁxed neighbourhood range k, the average overlap

of neighbourhoods of size k in the projection space

and the original data space are counted, leading to the

quality

(X,Y) =

∑

i=1



) ∩N

)



/(Nk) (4)

where N

) (resp. N

)) are the indices of the k

closest points of x

in the data space (resp. projection

space). Interestingly, the quality summarises various

popular alternative evaluation measures (Lee and Ver-

leysen, 2009). The neighbourhood degree k is crisp,

while the NeRV costs consider a smooth version in-

duced by the Gaussian, but still emphasising a certain

neighbourhood range by means of a ﬁxed choice of

the bandwidth.

Any reasonable dissimilarity measure d can be

used within this framework. As an example, in dis-

criminative dimensionality reduction, instead of the

standard euclidean metric, the so-called Fisher met-

ric is considered, which only takes into account data

changes as they affect a given labelling scheme, see

e.g. (Gisbrecht et al., 2014). This combination is re-

ferred to as Fisher-t-SNE.

Since NeRV is a non-parametric approach, we ob-

tain projection co-ordinates of the given data only.

The axes of the projection are widely arbitrary, and

no semantic meaning is attached to the visual display.

By incorporating metric learning, we aim at comple-

menting the visual display by a link to the original

data dimensions, such that the display can be accom-

panied by a semantic meaning in terms of the original

(usually interpretable) data dimensions.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

234

−2

−1

−0.5

0.5

Dim 1

Dim 2

Dim 3

C 1

C 2

C 3

−2 −1 0 1 2 3

−3

−2

−1

Dim 1

Dim 2

C 1

C 2

C 3

−1.5 −1 −0.5 0 0.5 1 1.5 2

−2

−1.5

−1

−0.5

0.5

1.5

Dim 1

Dim 2

C 1

C 2

C 3

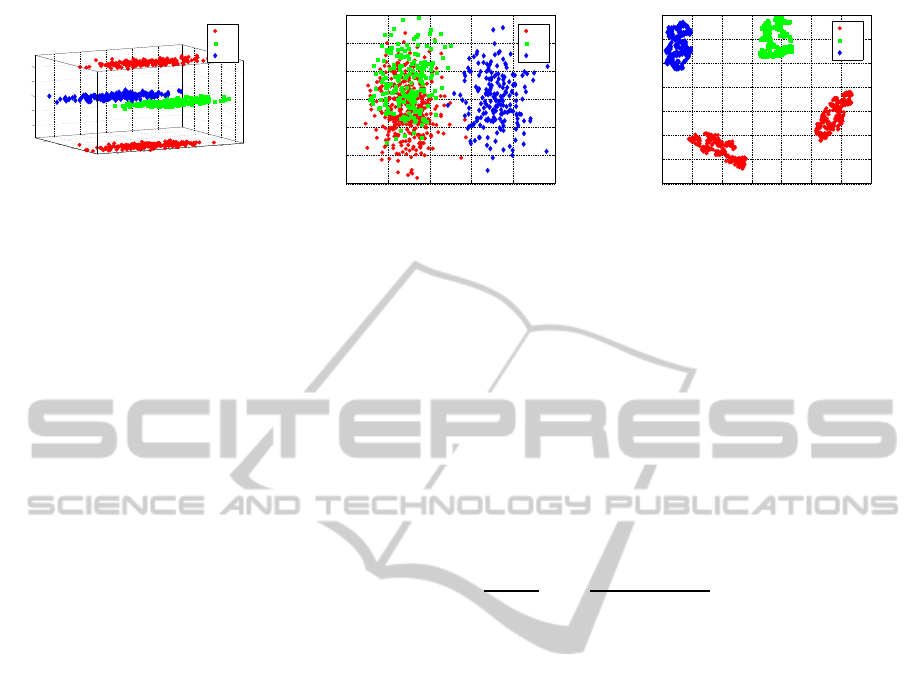
Figure 1: Artiﬁcial multimodal data (left), projection by LDA (middle), projection by Fisher t-SNE (right).

3 METRIC LEARNING

Assume a ﬁxed data projection X 7→ Y is given. For

metric learning, the idea is to change the metric of the

data representation in X such that the chosen metric

best resembles the information which is inherent in

this given non-parametric mapping.

We consider a global quadratic form for X

)

= (x

− x

)

Λ(x

− x

) (5)

with a positive semideﬁnite matrix

Λ = Ω

Ω (6)

The goal is to learn Λ (or equivalently Ω) such that it

best resembles the given visual display. Provided this

metric change captures the relevant information of the

visual display, it enables two things:

• It is possible to judge the relevance of the data

dimensions for the given display by inspecting the

relevance terms

∑

Ω

(7)

and hence gives a semantic interpretation of the

display by linking it to the most relevant data di-

mensions (the ones with largest Λ

• It is possible to transform the data

X 7→ ΩX (8)

to obtain data representations which more closely

resemble the projections of the data in two dimen-

sions; this opens the possibility to imprint infor-

mation on the data based on the visual interface.

How can we obtain a suitable matrix Λ? Mimicking

the successful approach of relevance learning which

has been established in supervised machine learning

(Biehl et al., 2009), we optimise Λ such that the ob-

jective as imposed by NeRV is optimised by an ad-

justment of Λ, together with a suitable regularisation:

E(Ω) = Q

NeRV

(ΩX,Y) + δ· trace(Λ) (9)

where δ > 0 constitutes a small positive value which

enforces solutions with a small norm for regularisa-

tion. Since the projection points y

are ﬁxed, we set σ

in both spaces such that the ﬁxed neighbourhood size

k is reached. While optimisation with a gradient tech-

nique is possible, we use an adaptive step size similar

to well-known algorithms from neural network opti-

misation (Riedmiller and Braun, 1993). Note that the

derivatives of the costs E(Ω) can be computed based

on the derivative of NeRV itself (Venna et al., 2010)

using the following equality and symmetry of NeRV

with respect to data points and projections

∂E(Ω)

∂Ω

∑

NeRV

(ΩX,Y)

∂(Ωx

)

· (x

)

+ 2· δ · Ω

(10)

The transformation matrix Ω is not unique since

the costs are invariant with respect to orthonormal

transformations of the matrix. This does not affect

its trace (and hence the relevance terms which will be

interpreted), however. Further, the result is not neces-

sarily unique due to possible local optima of the costs

which are inherent in NeRV; in practice, we did not

observe problems.

4 EXPERIMENTS

We investigate the possibility to substantiate a given

visual display of data by metric learning, leading to

relevance factors which allow a meaningful insight

into the relevance of the data dimensionalities for the

display, and leading to a more suitable representation

of the data which imprints the informationas provided

by the visual display. While we can evaluate the for-

mer with a reference to the gained semantic insight,

we evaluate the latter by the coranking framework

which compares the neighbourhood structure induced

by the data representation and the visual display, re-

spectively (Lee et al., 2013). We consider the follow-

ing three data sets:

Multimodal: data refers to an artiﬁcially generated

data set with known ground truth. Data are three

MetricLearninginDimensionalityReduction

235

dimensional, belonging to 3 classes, whereby one

class is multimodal, see Fig. 1 (left). Dimension 1

is irrelevant for the cluster formation, dimension

2 discriminates the classes, dimension 3 discrimi-

nates the two modes in class 1.

Diabetes: data refers to a data set describing 442 pa-

tients by 10 features (age, sex, BMI, blood pres-

sure, 6 measurements taken from blood serum)

with a labelling according to diabetes progression

after one year. The data set has been used in

(Efron et al., 2004), where a modern feature se-

lection technique has marked three of the criteria

as particularly relevant for the prediction task.

Adrenal: data refers to a data set of 147 pa-

tients characterised by 32 features (various steroid

markers), where labelling is given by two different

types of adrenal cancer, see (Biehl et al., 2012).

Artiﬁcial Multimodal Data

We project the given data to two dimensions in two

different ways: on the one hand, a linear discriminant

analysis (LDA) is used, which projects the data lin-

early to the plane, preserving classes as indicated by

the labels as much as possible. Since it relies on a uni-

modal Gaussian for every class, LDA is not capable

of preserving the multi modality of class one, result-

ing in an overlap of classes one and two. In com-

0 100 200 300 400 500 600 700 800

0.5

1.5

2.5

Neighborhood size

NeRV

Dim 1

Dim 2

Dim 3

0 100 200 300 400 500 600 700 800

0.5

1.5

2.5

3.5

Neighborhood size

NeRV

Dim 1

Dim 2

Dim 3

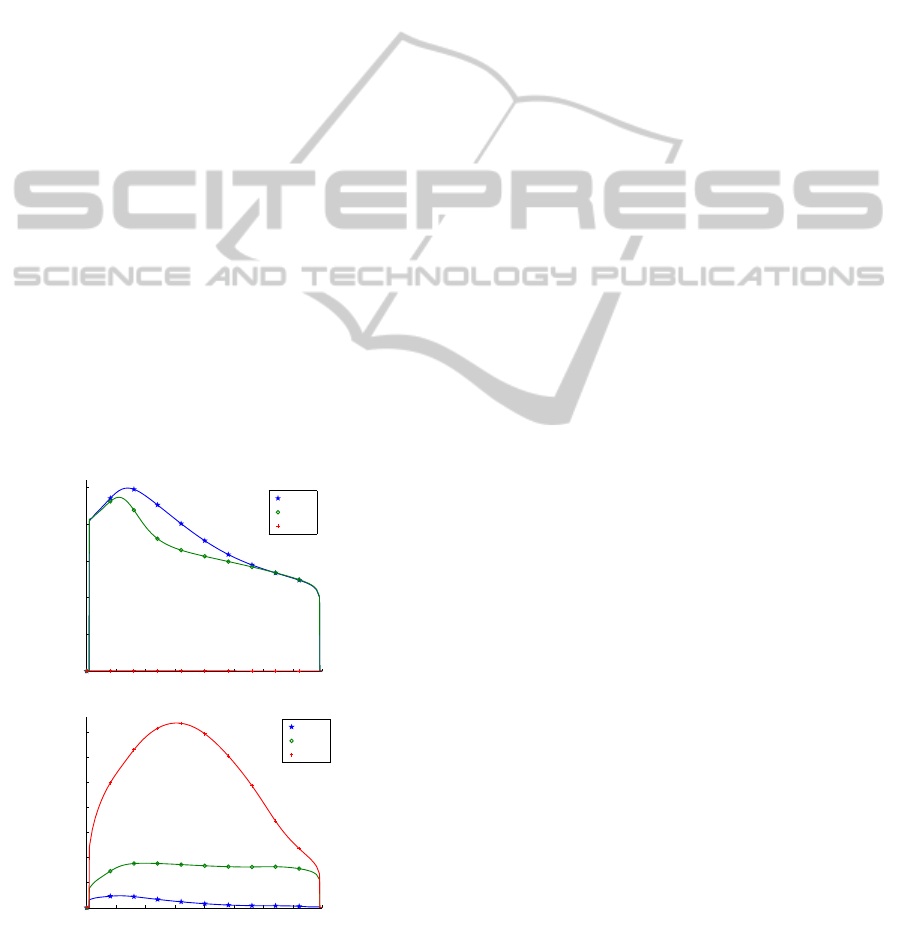
Figure 2: Relevances Ω

obtained by the proposed method

for the LDA projection in dependency of the choice k of the

cost function E(Ω) (left), for the projection by Fisher t-SNE

(right).

parison, we use the non-linear projection technique

t-SNE which is applied to the data as characterised

by the Fisher information metric to take the label in-

formation into account (see (Gisbrecht et al., 2014)).

The Fisher information metric curves the space lo-

cally such that the information most relevant to the

given labelling is emphasised. On top of this curva-

ture, t-SNE emphasises the cluster structure and ﬁnds

a corresponding two dimensional projection, display-

ing all four modes present in the data set (see Fig. 1).

We learn a global quadratic form using the tech-

nique as described above, whereby we report the ob-

tained result for different degrees of neighbourhood

k for the costs E(k). The relevance terms Λ

for

i ∈ {1,2,3} and the two different projections are de-

picted in Fig. 2. The relevance terms clearly con-

ﬁrm the expectations if one interprets these two pro-

jections: LDA ignores the separation induced by the

third dimension, treating the remaining two dimen-

sions as equally important; this results in the failure

to separate classes one and two. Fisher-t-SNE, in

contrast, neglects the ﬁrst dimension, which does not

contain structure, but emphasises the other two, such

that all data modes are preserved. The relevanceterms

mirror this interpretation for all but extremal choices

of the neighbourhood degree k.

This example also elucidates the fact that matrix

learning for a given visual display is different from

feature selection: rather than emphasising factors rel-

evant for a given labelling, the proposed framework

identiﬁes factors which best explain the given visual

display. These factors can coincide with the factors

identiﬁed by feature selection provided the visual dis-

play emphasises the given class labelling, but in gen-

eral, this is not the case.

Diabetes Data

We project the given data using t-SNE to two dimen-

sions. One can observe a correlation of the output

and one projection axes, which is overlaid by a two

cluster structure orthogonal to the output label (see

Fig. 3 (left)). The t-SNE projection displays a reason-

able quality as evaluated by the co-ranking framework

(see Fig. 3 (middle/right)). In comparison, we trans-

form the data according to the learned quadratic form

for a neighbourhood 10 and 50, respectively. As can

be seen via the coranking framework, the transformed

data, albeit relying on a linear transform only, much

better resembles the information shown in the visual

display. This conﬁrms the possibility of imprinting

information from the visual display to the given data

representation for this medical data set.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

236

−4 −2 0 2 4

−2

−1

Dim 1

Dim 2

10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Neighborhood size

Quality

X ⋅ Ω

10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Neighborhood size

Quality

X ⋅ Ω

Figure 3: T-SNE projection of the diabetes data set (left), quality for the t-SNE mapping for the standard euclidean metric

versus the transformed data with relevance matrix for neighbourhood range 10 (middle) and 50 (right).

−4 −2 0 2 4

−2

−1

Dim 1

Dim 2

ACA

ACC

−3 −2 −1 0 1 2

−3

−2

−1

Dim 1

Dim 2

ACA

ACC

0 5 10 15 20 25 30 35

0.5

1.5

2.5

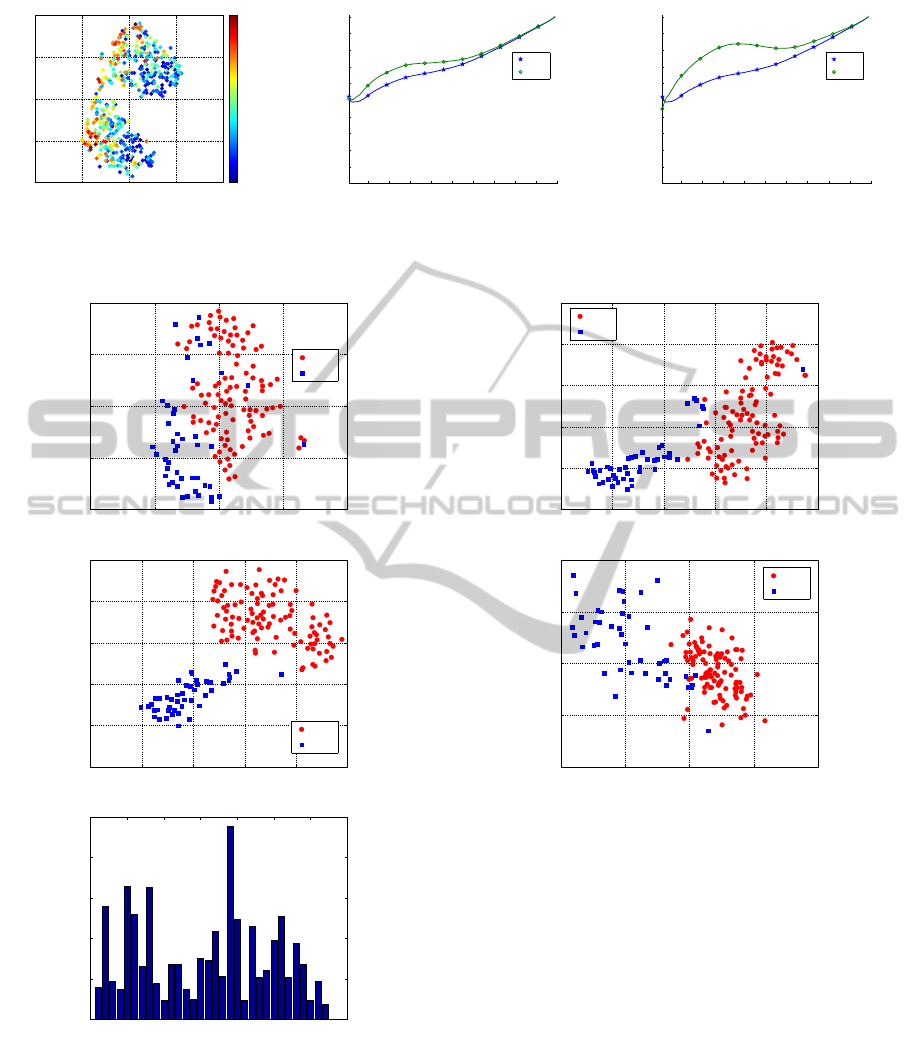
Figure 4: Projection of the adrenal data using t-SNE (top)

and Fisher t-SNE (middle). The latter can be used to learn

the relevant factors for this discriminative visual display

(bottom).

Adrenal Data

For the adrenal data, we consider a projection of the

original data by Fisher t-SNE, compared to a projec-

−15 −10 −5 0 5 10

−10

−5

Dim 1

Dim 2

ACA

ACC

−4 −2 0 2 4

−4

−2

Dim 1

Dim 2

ACA

ACC

Figure 5: Projection of the linearly transformed adrenal data

using t-SNE (top) Projection to the two main eigenvectors

of the learned linear transformation (bottom).

tion of the data by standard t-SNE (see Fig. 4). In-

terestingly, the 1-nearest neighbour classiﬁcation er-

ror of the original data set is 10.9%, as also mir-

rored in the t-SNE projection which displays quite

some overlap of the data, while the error drops down

to only 0.7% for the Fisher t-SNE projection. We

can imprint the information available in this discrim-

inative projection to the data by means of relevance

learning, as before. We learn a quadratic form with

neighbourhood range k = 10 of the costs, resulting

in relevance factors which strongly resemble the ﬁnd-

ings as described in the publication (Biehl et al.,

2012). This proﬁle is very consistent for different

choices of neighbourhood range k (we tested values

k ∈ {10, 20,40} which lead to qualitatively the same

result). As before, we can imprint this information

MetricLearninginDimensionalityReduction

237

onto the original data by means of an according data

transformation. The t-SNE projection of the linearly

transformed data is depicted in Fig. 5, the 1-nearest

neighbour error reduces to 3.4% (as compared to trice

as much for the original data). Note that, unlike the

Fisher information metric, the data are subject to a

simple linear data transform only as regards its rep-

resentation, followed by the non-parametric t-SNE

mapping. Interestingly, the obtained linear data trans-

formation even suggests a linear data display with al-

most the same quality: Fig. 5 also displays the linear

projection to the ﬁrst two eigenvalues of the learned

data transformation. The 1-nearest neighbour error is

2.7% only, enabling a very efﬁcient representation of

the data which mirrors the underlying label informa-

tion. For both cases, one point is clearly indicated

as an outlier (possibly corresponding to a mislabeling

of the data point, as also discussed in the publication

(Biehl et al., 2012)). Due to its possibility to follow

strong nonlinearities caused by its non-parametric na-

ture, the Fisher information metric itself tends to over-

ﬁt in this region, such that this outlier is much less

pronounced in the Fisher t-SNE mapping (Fig. 4).

Resumee

We have investigated three data sets as concerns the

possibility to link its visual display to explicit rele-

vance terms which link the displayed points to a se-

mantic meaning, and which open an interface towards

imposing this information to the data representation

by means of a linear transform. The tasks at hand be-

ing unsupervised, the evaluation of these possibilities

it not straightforward. In our experiments, we demon-

strated the claims in the following way:

• We evaluated the matrix learning framework for

an artiﬁcial data set with known relevances for the

given visual displays. The found relevances con-

ﬁrm the expectation in these settings.

• We evaluated the possibility to imprint the infor-

mation shown in the visual display to the data by

means of a linear data transformation by using the

co-ranking framework for data visualisation for

one real life data set.

• We evaluated the possibility to imprint the in-

formation as shown in the visual display by a

reference to the nearest neighbour error in the

case of an initial supervised dimensionality reduc-

tion. Here, the transformed data clearly allow to

achieve a better nearest neighbour error, i.e. a data

transformation as learned from the initial discrim-

inative visual display of the data enables us to ob-

tain an alternative data representation which bet-

ter resembles this important aspect. Thereby, due

to the linearity of the transformation, a semantic

interpretation of the axes is still possible.

So far, by restricting to a global quadratic form, the in-

duced data transformation is linear. Note that, similar

to proposals in supervised metric learning, a generali-

sation of the approach to locally quadratic forms (and

hence a globally non-linear data projection) would be

possible (Bellet et al., 2013).

5 CONCLUSIONS

We have introduced relevance learning into dimen-

sionality reduction as an efﬁcient concept to accom-

pany a given visual display by the possibility to judge

the relevance of data dimensions for the given map-

ping. Besides a better interpretability of the mapping,

we have shown how this framework can be used as an

interface to change data representations by means of

visual displays, e.g. by incorporating label informa-

tion into the pipeline. This opens the way for future

work in particular in two aspects: on the one hand,

we are working on local matrix variants, which al-

low a richer representation of globally non-linear de-

pendencies, and its corresponding visual display. On

the other hand, we are investigating how the proposed

framework can efﬁciently be integrated into an inter-

active pipeline, where online adaptation of the display

according to a new metric is a central demand.

ACKNOWLEDGEMENTS

Funding by DFG under grant number HA 2719/7-1

and by the CITEC centre of excellence are gratefully

acknowledged.

REFERENCES

Bellet, A., Habrard, A., and Sebban, M. (2013). A survey

on metric learning for feature vectors and structured

data. CoRR, abs/1306.6709.

Biehl, M., Hammer, B., Mer´enyi, E., Sperduti, A., and

Villmann, T., editors (2011). Learning in the con-

text of very high dimensional data (Dagstuhl Seminar

11341), volume 1.

Biehl, M., Hammer, B., Schneider, P., and Villmann, T.

(2009). Metric learning for prototype based clas-

siﬁcation. In Bianchini, M., Maggini, M., and

Scarselli, F., editors, Innovations in Neural Informa-

tion – Paradigms and Applications, Studies in Com-

putational Intelligence 247, pages 183–199. Springer.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

238

Biehl, M., Schneider, P., Smith, D., Stiekema, H., Tay-

lor, A., Hughes, B., Shackleton, C., Stewart, P., and

Arlt, W. (2012). Matrix relevance lvq in steroid

metabolomics based classiﬁcation of adrenal tumors.

In ESANN.

Brown, E. T., Liu, J., Brodley, C. E., and Chang, R.

(2012). Dis-function: Learning distance functions in-

teractively. In Visual Analytics Science and Technol-

ogy (VAST), 2012 IEEE Conference on, pages 83–92.

IEEE.

Bunte, K., Biehl, M., and Hammer, B. (2012a). A general

framework for dimensionality reducing data visualiza-

tion mapping. Neural Computation, 24(3):771–804.

Bunte, K., Schneider, P., Hammer, B., Schleif, F.-M., Vill-

mann, T., and Biehl, M. (2012b). Limited rank matrix

learning, discriminative dimension reduction and vi-

sualization. Neural Networks, 26:159–173.

Committee on the Analysis of Massive Data, Committee on

Applied and Theoretical Statistics, Board on Mathe-

matical Sciences and Their Applications, Division on

Engineering and Physical Sciences, and National Re-

search Council (2013). Frontiers in Massive Data

Analysis. National Academic Press.

Efron, B., Hastie, T., Johnstone, I., and Tibshirani, R.

(2004). Least angle regression. Annals of Statistics,

32:407–499.

Endert, A., Fiaux, P., and North, C. (2012). Semantic inter-

action for visual text analytics. In Proceedings of the

SIGCHI Conference on Human Factors in Computing

Systems, pages 473–482. ACM.

Gisbrecht, A. and Hammer, B. (2014). Data visualization

by nonlinear dimensionality reduction. WIREs Data

Mining and Knowledge Discovery.

Gisbrecht, A., Schulz, A., and Hammer, B. (2014). Para-

metric nonlinear dimensionality reduction using ker-

nel t-sne. Neurocomputing.

Goldberger, J., Roweis, S., Hinton, G., and Salakhutdinov,

R. (2004). Neighbourhood components analysis. In

Advances in Neural Information Processing Systems

17, pages 513–520. MIT Press.

Hammer, B., Gisbrecht, A., and Schulz, A. (2013). Appli-

cations of discriminative dimensionality reduction. In

ICPRAM.

Hammer, B., He, H., and Martinetz, T. (2014). Learning and

modeling big data. In Verleysen, M., editor, ESANN,

pages 343–352.

Jin, Y. and Hammer, B. (2014). Computational intelligence

in big data [guest editorial]. IEEE Comp. Int. Mag.,

9(3):12–13.

Khalil, T. (2012). Big data is a big deal. White House.

Lee, J. and Verleysen, M. (2009). Quality assessment of

dimensionality reduction: Rank-based criteria quality

assessment of dimensionality reduction: Rank-based

criteria quality assessment of dimensionality reduc-

tion: Rank-based criteria quality assessment of di-

mensionality reduction: rank-based criteria. Neuro-

computing, 72(7-9):1431–1443.

Lee, J. A., Renard, E., Bernard, G., Dupont, P., and Verley-

sen, M. (2013). Type 1 and 2 mixtures of kullback-

leibler divergences as cost functions in dimensional-

ity reduction based on similarity preservation. Neuro-

computing, 112:92–108.

Lee, J. A. and Verleysen, M. (2007). Nonlinear dimension-

ality reduction. Springer.

Lee, J. A. and Verleysen, M. (2010). Scale-independent

quality criteria for dimensionality reduction. Pattern

Recognition Letters, 31:2248–2257.

Mokbel, B., Paassen, B., and Hammer, B. (2014). Adaptive

distance measures for sequential data. In Verleysen,

M., editor, ESANN, pages 265–270.

Peltonen, J., Sandholm, M., and Kaski, S. (2013). Infor-

mation retrieval perspective to interactive data visual-

ization. In Hlawitschka, M. and Weinkauf, T., editors,

Proceedings of Eurovis 2013, The Eurographics Con-

ference on Visualization. The Eurographics Associa-

tion.

Riedmiller, M. and Braun, H. (1993). A direct adap-

tive method for faster backpropagation learning: The

rprop algorithm. In Proceedings of the IEEE Inter-

national Conference on Neural Networks, pages 586–

591. IEEE Press.

Roweis, S. T. and Saul, L. K. (2000). Nonlinear dimen-

sionality reduction by locally linear embedding. SCI-

ENCE, 290:2323–2326.

R¨uping, S. (2006). Learning Interpretable Models. PhD

thesis, Dortmund University.

Schulz, A., Gisbrecht, A., and Hammer, B. (2014). Rele-

vance learning for dimensonality reduction. In Ver-

leysen, M., editor, ESANN, pages 165–170.

Simoff, S. J., B¨ohlen, M. H., and Mazeika, A., editors

(2008). Visual Data Mining - Theory, Techniques and

Tools for Visual Analytics, volume 4404 of Lecture

Notes in Computer Science. Springer.

Tenenbaum, J., da Silva, V., and Langford, J. (2000). A

global geometric framework for nonlinear dimension-

ality reduction. Science, 290:2319–2323.

van der Maaten, L. and Hinton, G. (2008). Visualizing

high-dimensional data using t-sne. Journal of Ma-

chine Learning Research, 9:2579–2605.

van der Maaten, L., Postma, E., and van den Herik, H.

(2009). Dimensionality reduction: A comparative re-

view. Technical report, Tilburg University Technical

Report, TiCC-TR 2009-005.

Vellido, A., Martin-Guerroro, J., and Lisboa, P. (2012).

Making machine learning models interpretable. In

ESANN’12.

Venna, J., Peltonen, J., Nybo, K., Aidos, H., and Kaski, S.

(2010). Information retrieval perspective to nonlinear

dimensionality reduction for data visualization. Jour-

nal of Machine Learning Research, 11:451–490.

Ward, M., Grinstein, G., and Keim, D. A. (2010). Interac-

tive Data Visualization: Foundations, Techniques, and

Application. A. K. Peters, Ltd.

Yang, Z., Peltonen, J., and Kaski, S. (2013). Scalable opti-

mization of neighbor embedding for visualization. In

ICML (2), volume 28 of JMLR Proceedings, pages

127–135. JMLR.org.

Zhai, Y., Ong, Y.-S., and Tsang, I. (2014). The emerg-

ing ”big dimensionality”. Computational Intelligence

Magazine, IEEE, 9(3):14–26.

MetricLearninginDimensionalityReduction

239