Nonlinear Models of BPSK Costas Loop

E. V. Kudryashova

, O. A. Kuznetsova

, N. V. Kuznetsov

1,2

, G. A. Leonov

, S. M. Seledzhi

M. V. Yuldashev

1,2

and R. V. Yuldashev

1,2

Faculty of Mathematics and Mechanics, Saint-Petersburg State University,

Universitetsky pr. 28, Saint-Petersburg, 198504, Russia

Dept. of Mathematical Information Technology, University of Jyv

askyl

a, P.O. Box 35 (Agora), FIN-40014, Finland

Keywords:

Costas Loop, BPSK, PLL, Phase-locked Loop, Simulation, Nonlinear Analysis.

Abstract:

Rigorous nonlinear analysis of the physical model of Costas loop is very difﬁcult task, so for analysis, simpli-

ﬁed mathematical models and numerical simulation are widely used. In the work it is shown that the use of

simpliﬁed mathematical models, and the application of non rigorous methods of analysis may lead to wrong

conclusions concerning the operability of Costas loop.

1 INTRODUCTION

The Costas loop is a classical phase-locked loop

(PLL) based circuit for carrier recovery (Costas,

1956; Costas, 1962). Nowadays various modiﬁca-

tions of Costas loop circuit are used in many com-

munication devices, e.g. Global Positioning Systems

(GPS) (Kaplan and Hegarty, 2006). In the paper the

classical analog Costas loop (Costas, 1956; Gardner,

1966; Lindsey, 1972; Best, 2007), used for BPSK de-

modulation, is considered (similar analysis can also

be done for QPSK Costas loop).

Costas loop is essentially a nonlinear control sys-

tem and its physical model is described by a nonlinear

non-autonomous discontinuous system of differential

equations (mathematical model in the signal space).

This system is a slow-fast system since there is con-

sidered simultaneously both very fast time scale of

signals and slow time scale of phase difference be-

tween the signals.

Thus in practice, for the analysis of Costas loop it

is widely used various simpliﬁed mathematical mod-

els and their numerical simulation (Costas, 1956;

Gardner, 1966; Lindsey, 1972; Best, 2007; Best et al.,

2014b).

In the work it is shown that 1) the use of simpliﬁed

mathematical models, and 2) the application of non

rigorous methods of analysis (e.g., a simulation) may

lead to wrong conclusions concerning the operability

of physical model of Costas loop.

To demonstrate this, below Costas loop operation

will be considered in details.

2 BPSK COSTAS LOOP

OPERATION

Consider Costas loop operation (see Fig. 1) after tran-

sient processes.

g(t)≡const

LPF1

LPF2

Loop ﬁlter

VCO

sin(ωt-θ

)

m(t)sin(ωt)

data

carrier

(m(t)cos(θ

)-m(t)cos(2ωt-θ

))

(m(t)sin(θ

)+m(t)sin(2ωt-θ

))

input

φ(t)≡φ(θ

)

Figure 1: Costas loop is in lock (the case of nonequal fre-

quencies of input carrier and free running VCO output):

there is a constant phase difference θ

∆

after synchroniza-

tion.

The input signal is BPSK signal, which is a prod-

uct of the transferred data m(t) = ±1 and the har-

monic carrier sin(ωt) with a high frequency ω. Since

the Costas loop is considered to be in the locked state,

VCO (Voltage-Controlled Oscillator) signal is syn-

chronized with the carrier.

Assumption 1. The terms, whose frequency is about

twice the carrier frequency, do not affect the synchro-

nization of the loop.

By Assumption 1 the outputs of low-pass ﬁlters

LPF1 and LPF2 can be approximated in the follow-

ing way. After the multiplication of VCO signal and

the input signal by multiplier block (⊗) on the upper

branch one has

704

Kudryasoha E., Kuznetsova O., Kuznetsov N., Leonov G., Seledzhi S., Yuldashev M. and Yuldashev R..

Nonlinear Models of BPSK Costas Loop.

DOI: 10.5220/0005050707040710

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 704-710

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

g(t)

(t)

LPF1

LPF2

Loop ﬁlter

VCO

sin(θ

(t))

data

carrier

(t)= m(t)(cos(θ

(t))-cos(θ

(t)+θ

(t)))

input

φ(t)≈ sin(2θ

(t))

m(t)sin(θ

(t))

(t)= m(t)(sin(θ

(t))+sin(θ

(t)+θ

(t)))

Figure 2: Costas loop is out of lock: there is time-varying phase difference θ

∆

(t) = θ

(t) − θ

(t).

(t) =



m(t) cos(0) − m(t)cos(2ωt)





m(t) − m(t)cos(2ωt)



≈

m(t),

(1)

i.e the upper loop works as demodulator. On the lower

branch the output signal of VCO, shifted by 90

◦

, is

multiplied by the input signal:

(t) = m(t) sin(ωt)cos(ωt) =



m(t) sin(0) + m(t)sin(2ωt)



m(t) sin(2ωt) ≈ 0.

(2)

Since after a transient processes there is no phase

difference, the control signal at the input of VCO,

which is used for VCO frequency adjustment to the

frequency of input carrier signal, has to be constant:

g(t) = const. (3)

Consider Costas loop before synchronization (see

Fig. 2) in the case when the phase of the input carrier

(t) and the phase of VCO θ

(t) are different:

∆

(t) = θ

(t) − θ

(t) 6= 0. (4)

In this case the signals ϕ

1,2

(t) on the upper and lower

branches can be approximated as

(t) =

m(t)



cos(θ

(t) − θ

(t)) − cos(θ

(t) + θ

(t))



≈

m(t)cos(θ

∆

(t)),

(t) =

m(t)



sin(θ

(t) − θ

(t)) + sin(θ

(t) + θ

(t))



≈

m(t)sin(θ

∆

(t)).

(5)

Assumption 2. The data signal m(t) does not affect

the synchronization of the loop.

Thus after multiplication of the outputs of LPF1

and LPF2 the transmitted data m(t) is neglected in the

signal ϕ(t), i.e. one has m(t)

= (±1)

= 1.

Approximations (6) depend on the phase differ-

ence of signals, i.e. two multiplier blocks (⊗) on the

upper and lower branches operate as phase detectors.

Caveat to Assumptions. Low-pass ﬁlters can not

operate perfectly, especially, during the moments of

changing m(t), therefore the data pulse shapes are no

longer ideal rectangular pulses after ﬁltration due to

distortion, created by the low-pass ﬁlters. This can

lead to incorrect conclusions on the performance of

the loop. One of such known examples is so-called

false-lock: while for m(t) ≡ const the loop acquires

lock and proper synchronization of the carrier and

VCO frequencies, for time-varying m(t) 6= const the

loop can acquire lock without proper synchronization

of the frequencies (false lock) (Olson, 1975; Simon,

1978; Hedin et al., 1978). To avoid such undesirable

situation one may try to choose loop parameters in

such a way that the synchronization time is less than

the time between changes in the data signal m(t) or to

modify the loop design (see, e.g., (Olson, 1975)).

Finally, by Assumption 2, one can use the follow-

ing approximation for the input of loop ﬁlter

ϕ(t) ≈ ϕ(θ

∆

(t)) =

sin(2θ

∆

(t)). (6)

Such an approximation, which depends on the phase

difference of signals, is called a phase detector char-

acteristic of Costas loop.

The relation between the input ϕ(t) and the output

g(t) of linear loop ﬁlter (Thede, 2005) has the form

= Ax + bϕ(t), g(t) = c

∗

x + hϕ(t),

(7)

where A is a constant matrix, the vector x(t) is a ﬁl-

ter state, b,c are constant vectors, h is constant, and

x(0) is initial state of ﬁlter. The control signal g(t)

is used to adjust VCO frequency to the frequency of

input carrier signal

(t) = ω

free

+ Lg(t). (8)

Here ω

f ree

is free-running frequency of VCO and L is

VCO gain.

If the frequency of input carrier is a constant:

(t) = ω

(t) ≡ ω

, (9)

then equations (7)-(9) give the following mathemati-

cal model of Costas loop:

NonlinearModelsofBPSKCostasLoop

705

˙x = Ax + bϕ(θ

∆

= ω

∆

− L(c

∗

x) − Lhϕ(θ

∆

(10)

where θ

∆

(t) = θ

(t)−θ

(t) and ϕ(θ

∆

) corresponds to

expression (7). Note that the initial frequencies differ-

ence (at t = 0) has the form

∆

(0) = ω

∆

+ Lc

∗

x(0) + Lhϕ(θ

∆

(0)). (11)

Here to consider one-dimensional stability ranges de-

ﬁned only by |ω

∆

| (see, e.g., capture and hold ranges)

it is necessary to assume that h = 0 and x(0) = 0.

For high-order ﬁlter, two different initial states ˜x(0)

and

˜x(0) may lead to identical values of α

(0, ˜x(0)) =

(0,

˜x(0)) but different functions α

(t, ˜x(0)) and

(t,

˜x(0)) (to avoid this effect it is possible to require

the observability of system (8)).

G(t)

Loop ﬁlter

VCO

(t)

input

(t) φ(θ

(t))

Figure 3: Classical (simpliﬁed) mathematical model of

BPSK Costas loop in the signal’s phase space.

System (11) considered in the classical works

(Costas, 1962; Lindsey, 1972) and corresponds to the

block-diagram shown in Fig. 3, where ϕ(θ

∆

) is phase

detector (PD) characteristic of Costas loop for sinu-

soidal signals.

Since mathematical model of Costas loop (11) is

nonlinear, in practice, for its analysis numerical sim-

ulation and linearization are widely used (Gardner,

2005; Lindsey, 1972; Best, 2007). Note that the lin-

earization without justiﬁcation and the analysis of lin-

earized models of nonlinear control systems may re-

sult in incorrect conclusions

. Also the application

of standard numerical analysis of PLL-based circuits

cannot guarantee to ﬁnd undesired multiple steady-

state solutions: see, e.g., examples of hidden oscilla-

tions

See, e.g., counterexamples to the ﬁlter hypothesis,

hidden oscillations in counterexamples to Aizerman’s and

Kalman’s conjectures on the absolute stability of nonlinear

control systems (Bragin et al., 2011), and the Perron effects

of the largest Lyapunov exponent sign reversal for a non-

linear system and its linearization (Kuznetsov and Leonov,

2005; Leonov and Kuznetsov, 2007).

An attractor is called a hidden attractor if its basin

of attraction does not intersect with small neighborhoods

of equilibria, otherwise it is called a self-excited attractor.

For example, hidden attractors are attractors in the systems

with no-equilibria or with the only stable equilibrium (a

special case of multistability and coexistence of attractors);

they arise in the study of well-known fundamental problems

such as 16th Hilbert problem, Aizerman & Kalman conjec-

In the next section a rigorous mathematical ap-

proach to derivation of nonlinear mathematical model

of Costas loop will be discussed.

3 RIGOROUS MATHEMATICAL

APPROACH TO DERIVATION

OF NONLINEAR

MATHEMATICAL MODEL OF

COSTAS LOOP

The relation between the inputs ϕ

1,2

(t) and the out-

puts g

1,2

(t) of linear low-pass ﬁlters is as follows

(Thede, 2005)

1,2

= A

1,2

+ b

1,2

(t), g

1,2

(t) = c

∗

1,2

(12)

Here A

1,2

are constant matrices, the vectors x

1,2

(t) are

ﬁlter states, b

1,2

are constant vectors, and the vec-

tors x

1,2

(0) are initial states of ﬁlters. For the loop

ﬁlter one can consider more general equation (8).

Taking into account (13), (8), and (9), one obtains

the mathematical model in the signal space describing

the physical model of BPSK Costas loop:

˙x

= A

+ b

m(t) sin(θ

(t))sin(θ

˙x

= A

+ b

m(t) sin(θ

(t))cos(θ

˙x = Ax + b(c

∗

)(c

∗

= ω

f ree

+ L(c

∗

x) + Lh(c

∗

)(c

∗

(13)

Here θ

(0) is the initial phase shift of VCO, and the

vectors x

1,2

(0),x(0) are initial states of ﬁlters. Thus

the initial VCO frequency (at t = 0) has the form

(0) = ω

f ree

+ Lc

∗

x(0) + Lhc

∗

(0)c

∗

(0). (14)

The mathematical model in the signal space (14)

is nonlinear nonautonomous discontinuous differen-

tial system, so in general case its analytical study

is a difﬁcult task even for the continuous case when

m(t) ≡ const. Besides it is a slow-fast system, so its

numerical study is rather complicated for the high-

frequency signals. The problem is that it is necessary

to consider simultaneously both very fast time scale of

the signals sin(θ

1,2

(t)) and slow time scale of phase

difference between the signals θ

∆

(t), therefore one

very small simulation time-step must be taken over a

tures and in applied research of Chua circuits, drilling sys-

tem, phase-locked loop based circuits, aircraft control sys-

tems and others (Kuznetsov et al., 2010; Bragin et al., 2011;

Leonov et al., 2012; Kuznetsov et al., 2013; Andrievsky

et al., 2013; Leonov and Kuznetsov, 2013; Leonov et al.,

2014).

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

706

very long total simulation period (Goyal et al., 2006;

Abramovitch, 2008a; Abramovitch, 2008b).

To overcome these problems, in place of using As-

sumption 1 one can apply averaging methods (Krylov

and Bogolyubov, 1947; Mitropolsky and Bogolubov,

1961; Samoilenko and Petryshyn, 2004; Sanders

et al., 2007) and consider a simpliﬁed mathematical

model in the signal’s phase space. However, this re-

quires the consideration of constant data signal (As-

sumption 2) and constant frequency of input carrier

(10):

(t) = ω

t + θ

(0).

In this case (14) is equivalent to

˙x

= A

+ b

sin(ω

t + θ

(0))sin(ω

t + θ

(0) + θ

∆

˙x

= A

+ b

sin(ω

t + θ

(0))cos(ω

t + θ

(0) + θ

∆

˙x = Ax + b(c

∗

)(c

∗

∆

= ω

∆

− L(c

∗

x) − Lh(c

∗

)(c

∗

(15)

Assuming that input carrier is a high-frequency

signal (i.e. ω

is large), one can consider small pa-

rameter ε =

and apply classical averring theory for

the equations of low-pass ﬁlters. Thus one can obtain

a mathematical model of BPSK Costas loop in the sig-

nal’s phase space (see Fig. 4):

˙x

= A

cos(θ

∆

˙x

= A

sin(θ

∆

˙x = Ax + b(c

∗

)(c

∗

∆

= ω

∆

− L(c

∗

x) − Lh(c

∗

)(c

∗

(16)

g(t)

(t)

LPF1

LPF2

Loop ﬁlter

VCO

(t)

(θ

(t))= cos(θ

(t))

input

φ(t)≈ sin(2θ

(t))

(t)

(θ

(t))= sin(θ

(t))

Figure 4: Mathematical model of BPSK Costas loop in the

signal’s phase space

Remark that here the initial frequencies difference

(at t = 0)

∆

(0) = ω

∆

− Lc

∗

x(0) − Lhc

∗

(0)c

∗

(0) (17)

is the same for system (17) and system (16) and it

does not coincide with expression (18) for classical

system (11). Here to consider one-dimensional sta-

bility ranges deﬁned only by |ω

∆

| (see, e.g., capture

and hold ranges) it is necessary to assume that h = 0

and x(0) = x

(0) = x

(0) = 0.

In the general case one has to consider multi-

dimensional stability domain (ω

∆

,x(0), x

(0),x

(0)).

4 COUNTEREXAMPLES TO THE

ASSUMPTIONS

Note once more that various simpliﬁcations and the

analysis of linearized models of control systems may

result in incorrect conclusions

. At the same time the

attempts to justify analytically the reliability of con-

clusions, based on engineering approaches, and rigor-

ous study of nonlinear models are quite rare (see, e.g.,

(Abramovitch, 1990; Chang et al., 1993; Stensby,

1997; Shirahama et al., 1998; Watada et al., 1998;

Hinz et al., 2000; Wu, 2002; Piqueira and Mon-

teiro, 2003; Suarez and Quere, 2003; Margaris, 2004;

Vendelin et al., 2005; Banerjee and Sarkar, 2006;

Kudrewicz and Wasowicz, 2007; Wang et al., 2008;

Bueno et al., 2010; Wiegand et al., 2010; Stensby,

2011; Suarez et al., 2012; Sarkar et al., 2014; Chicone

and Heitzman, 2013; Yoshimura et al., 2013; Best

et al., 2014a)). One of the reasons is that “nonlin-

ear analysis techniques are well beyond the scope of

most undergraduate courses in communication the-

ory” (Tranter et al., 2010).

Further examples demonstrate that the use of As-

sumptions 1-2 requires further study and rigorous jus-

tiﬁcation. The following examples demonstrate that

for the same parameters the behaviors of considered

models

• physical model (with data signal and low-pass ﬁl-

ters) or its mathematical model in the signal space

(Figs. 2,5 and system (14))

• simpliﬁed mathematical model in the signal space

(without data signal and with low-pass ﬁlters))

(Figs. 2,5 with m(t) = const and system (16));

• simpliﬁed mathematical model the signal’s phase

space (with low-pass ﬁlters and without data sig-

nal) (Fig. 4 and system (17));

• classical mathematical model the signal’s phase

space (without low-pass ﬁlters and data signal)

(Fig. 3 and system (11))

may be very different from each other.

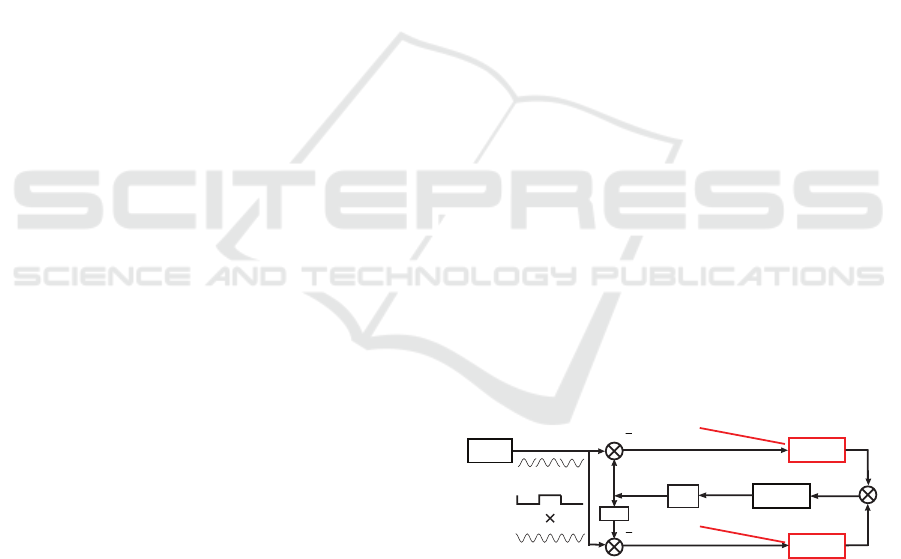
Simulation Parameters. Low pass ﬁlters transfer

functions H

l p f

(s) =

s/ω

, ω

= 1.2566 ∗ 10

and

corresponding equations (8) parameters are A

1,2

−ω

, b

1,2

= 1, c

1,2

= 1; Loop ﬁlter transfer function

l f

(s) =

s+1

, τ

= 3.9789 ∗ 10

−6

, τ

= 2 ∗ 10

−5

see also counterexamples to the ﬁlter hypothesis, Aiz-

erman’s and Kalman’s conjectures on the absolute stability

of nonlinear control systems (Kuznetsov et al., 2011; Bra-

gin et al., 2011; Leonov and Kuznetsov, 2013), and the Per-

ron effects of the largest Lyapunov exponent sign inversions

(Kuznetsov and Leonov, 2005; Leonov and Kuznetsov,

2007), etc.

NonlinearModelsofBPSKCostasLoop

707

lpf

(s)

lpf

(s)

sin(θ (t))

m(t)sin(θ (t))

(t)

input

x(0)

(0)

sin

free

(m(t)cos(θ

(t))-m(t)sin(θ

(t)+θ

(t)))

φ(t)≈ sin(2θ

(t))

(m(t)sin(θ

(t))+m(t)sin(θ

(t)+θ

(t)))

g(t)

(t)

Figure 5: Block-diagram of Costas loop mathematical model in the signal space described by transfer functions and initial

conditions.

-0.9

-0.6

-0.3

0.02 0.04

Figure 6: Loop ﬁlter output g(t) for averaged model (17)

(black) and physical model (red) in Fig. 2.

and corresponding differential equations (8) parame-

ters are A = 1, b = 0, c =

, h =

; carrier frequency

is ω

= 2∗ π ∗ 400000 and initial carrier phase is zero:

(0) = 0.

Example 1. In Fig. 6 is shown that Assumption 1 may

not be valid: while simpliﬁed mathematical model in

the signal’s phase space (17) (see Fig. 4) acquires

lock (black), physical model (14) (see Fig. 5) is out

of lock (red).

Here VCO free-running frequency: ω

f ree

3.5500 ∗ 10

; initial states of ﬁlters are all zero

(t) = x(0) = x

(0) = x

0 = 0.

Example 2. In Fig. 7 is shown that Assumption 2 may

not be valid: while simpliﬁed mathematical model in

the signal space (16) (see physical model in Fig. 5

with constant data signal m(t) ≡ 1) acquire lock

(black), physical model with periodic data signal (14)

-0.6

-0.4

-0.2

0.2

1 x10

-4

Figure 7: Loop ﬁlter output g(t) for physical model (black)

with periodic data signal, physical model (red) with con-

stant data signal m(t) ≡ 1.

(see Fig. 5) is out of lock (red).

Here VCO free-running frequency ω

f ree

3.0753 ∗ 10

, initial states of ﬁlters are all zero

(t) = x(0) = x

(0) = x

(0) = 0, data signal is pe-

riodic m(t) = sign sin(100000 ∗ 2 ∗ πt).

Example 3. In Fig. 8 is shown that low-pass ﬁlters

may affect stability of models in the signal’s phase

space: while simpliﬁed mathematical model the sig-

nals phase space (17) (see Fig. 4) is out of lock (red),

classical mathematical model the signals phase space

(11) (see Fig. 3), where low-pass ﬁlters are not taken

into account, acquires lock (black). Therefore the

consideration of classical (simpliﬁed) model in sig-

nal’s phase space (Fig. 3 and system (11)) may lead

to wrong conclusion.

Here VCO free-running frequency ω

f ree

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

708

-0.9

-0.7

-0.5

-0.3

-0.1

0.1

1 2 3 4 x10

-3

Figure 8: Loop ﬁlter output g(t) for signal’s phase space

model (black curve) without low-pass ﬁlters, signal’s phase

space model (red curve) with low-pass ﬁlters.

3.5133 ∗ 10

, initial states of ﬁlters are zero: α

(t) =

x(0) = x

(0) = x

(0), no data is being transmitted

m(t) = 1.

5 CONCLUSION

In the work it is shown that 1) the consideration

of simpliﬁed mathematical models, constructed intu-

itively by engineers, and 2) the application of non rig-

orous methods of analysis can lead to wrong conclu-

sions concerning the operability of Costas loop.

ACKNOWLEDGEMENTS

This work was supported by Saint-Petersburg State

University (project 6.39.416.2014).

REFERENCES

Abramovitch, D. (1990). Lyapunov redesign of analog

phase-lock loops. Communications, IEEE Transac-

tions on, 38(12):2197–2202.

Abramovitch, D. (2008a). Efﬁcient and ﬂexible simula-

tion of phase locked loops, part I: simulator design.

In American Control Conference, pages 4672–4677,

Seattle, WA.

Abramovitch, D. (2008b). Efﬁcient and ﬂexible simulation

of phase locked loops, part II: post processing and a

design example. In American Control Conference,

pages 4678–4683, Seattle, WA.

Andrievsky, B. R., Kuznetsov, N. V., Leonov, G. A., and

Pogromsky, A. Y. (2013). Hidden oscillations in air-

craft ﬂight control system with input saturation. IFAC

Proceedings Volumes (IFAC-PapersOnline), 5(1):75–

79.

Banerjee, T. and Sarkar, B. (2006). A new dynamic gain

control technique for speed enhancement of digital

phase locked loops (DPLLs). Signal Processing.,

86:1426–1434.

Best, R. E. (2007). Phase-Lock Loops: Design, Simulation

and Application. McGraw-Hill.

Best, R. E., Kuznetsov, N. V., Leonov, G. A., Yuldashev,

M. V., and Yuldashev, R. V. (2014a). Discontinuity

and Complexity in Nonlinear Physical Systems, vol-

ume 6, chapter Nonlinear analysis of phase-locked

loop based circuits. Springer.

Best, R. E., Kuznetsov, N. V., Leonov, G. A., Yuldashev,

M. V., and Yuldashev, R. V. (2014b). Simulation of

analog Costas loop circuits. International Journal of

Automation and Computing. accepted.

Bragin, V. O., Vagaitsev, V. I., Kuznetsov, N. V., and

Leonov, G. A. (2011). Algorithms for ﬁnding hid-

den oscillations in nonlinear systems. The Aizerman

and Kalman conjectures and Chua’s circuits. Jour-

nal of Computer and Systems Sciences International,

50(4):511–543.

Bueno, A., Ferreira, A., and Piqueira, J. (2010). Modeling

and ﬁltering double-frequency jitter in one-way mas-

terslave chain networks. IEEE transactions on circuits

and systemsI, 57(12):3104–3111.

Chang, F.-J., Twu, S.-H., and Chang, S. (1993). Global

bifurcation and chaos from automatic gain control

loops. Circuits and Systems I: Fundamental Theory

and Applications, IEEE Transactions on, 40(6):403–

412.

Chicone, C. and Heitzman, M. (2013). Phase-locked

loops, demodulation, and averaging approximation

time-scale extensions. SIAM J. Applied Dynamical

Systems, 12(2):674–721.

Costas, J. (1956). Synchoronous communications. In Proc.

IRE, volume 44, pages 1713–1718.

Costas, J. P. (1962). Receiver for communication system.

US Patent 3,047,659.

Gardner, F. (1966). Phase–lock techniques. John Wiley,

New York.

Gardner, F. (2005). Phaselock Techniques. Wiley.

Goyal, P., Lai, X., and Roychowdhury, J. (2006). A fast

methodology for ﬁrst-time-correct design of PLLs us-

ing nonlinear phase-domain VCO macromodels. In

Proceedings of the 2006 Asia and South Paciﬁc De-

sign Automation Conference, pages 291–296.

Hedin, G., Holmes, J., Lindsey, W., and Woo, K. (1978).

Theory of false lock in costas loops. Communications,

IEEE Transactions on, 26(1):1–12.

Hinz, M., Konenkamp, I., and Horneber, E.-H. (2000).

Behavioral modeling and simulation of phase-locked

loops for RF front ends. In Proc. 43rd BEE Midwest

Symp. on Circuits and Systems, pages 194–197. IEEE.

Kaplan, E. and Hegarty, C. (2006). Understanding GPS:

Principles and Applications. Artech House.

NonlinearModelsofBPSKCostasLoop

709

Krylov, N. and Bogolyubov, N. (1947). Introduction to non-

linear mechanics. Princeton Univ. Press, Princeton.

Kudrewicz, J. and Wasowicz, S. (2007). Equations of

Phase-Locked Loops: Dynamics on the Circle, Torus

and Cylinder, volume 59. World Scientiﬁc.

Kuznetsov, N., Kuznetsova, O., Leonov, G., and Vagait-

sev, V. (2013). Informatics in Control, Automation

and Robotics, Lecture Notes in Electrical Engineer-

ing, Volume 174, Part 4, chapter Analytical-numerical

localization of hidden attractor in electrical Chua’s cir-

cuit, pages 149–158. Springer.

Kuznetsov, N. V. and Leonov, G. A. (2005). On stabil-

ity by the ﬁrst approximation for discrete systems.

In 2005 International Conference on Physics and

Control, PhysCon 2005, volume Proceedings Volume

2005, pages 596–599. IEEE.

Kuznetsov, N. V., Leonov, G. A., and Seledzhi, S. M.

(2011). Hidden oscillations in nonlinear con-

trol systems. IFAC Proceedings Volumes (IFAC-

PapersOnline), 18(1):2506–2510.

Kuznetsov, N. V., Leonov, G. A., and Vagaitsev, V. I. (2010).

Analytical-numerical method for attractor localization

of generalized Chua’s system. IFAC Proceedings Vol-

umes (IFAC-PapersOnline), 4(1):29–33.

Leonov, G. A. and Kuznetsov, N. V. (2007). Time-varying

linearization and the Perron effects. International

Journal of Bifurcation and Chaos, 17(4):1079–1107.

Leonov, G. A. and Kuznetsov, N. V. (2013). Hidden attrac-

tors in dynamical systems. From hidden oscillations

in Hilbert-Kolmogorov, Aizerman, and Kalman prob-

lems to hidden chaotic attractors in Chua circuits. In-

ternational Journal of Bifurcation and Chaos, 23(1).

art. no. 1330002.

Leonov, G. A., Kuznetsov, N. V., Kiseleva, M. A.,

Solovyeva, E. P., and Zaretskiy, A. M. (2014). Hidden

oscillations in mathematical model of drilling system

actuated by induction motor with a wound rotor. Non-

linear Dynamics, 77(1-2):277–288.

Leonov, G. A., Kuznetsov, N. V., and Vagaitsev, V. I. (2012).

Hidden attractor in smooth Chua systems. Physica D:

Nonlinear Phenomena, 241(18):1482–1486.

Lindsey, W. (1972). Synchronization systems in communi-

cation and control. Prentice-Hall, New Jersey.

Margaris, W. (2004). Theory of the Non-Linear Analog

Phase Locked Loop. Springer Verlag, New Jersey.

Mitropolsky, Y. and Bogolubov, N. (1961). Asymptotic

Methods in the Theory of Non-Linear Oscillations.

Gordon and Breach, New York.

Olson, M. (1975). False-lock detection in costas demodula-

tors. Aerospace and Electronic Systems, IEEE Trans-

actions on, AES-11(2):180–182.

Piqueira, J. R. C. and Monteiro, L. H. A. (2003). Con-

sidering second-harmonic terms in the operation of

the phase detector for second-order phase-locked

loop. IEEE Transactions On Circuits And Systems–

I, 50(6):805–809.

Samoilenko, A. and Petryshyn, R. (2004). Multifrequency

Oscillations of Nonlinear Systems. Mathematics and

Its Applications. Springer.

Sanders, J. A., Verhulst, F., and Murdock, J. (2007). Av-

eraging Methods in Nonlinear Dynamical Systems.

Springer.

Sarkar, B. C., Sarkar, S. S. D., and Banerjee, T. (2014).

Nonlinear dynamics of a class of symmetric lock

range DPLLs with an additional derivative control.

Signal Processing, 94:631 – 641.

Shirahama, H., Fukushima, K., Yoshida, N., and Taniguchi,

K. (1998). Intermittent chaos in a mutually coupled

pll’s system. Circuits and Systems I: Fundamen-

tal Theory and Applications, IEEE Transactions on,

45(10):1114–1117.

Simon, M. K. (1978). The false lock performance of costas

loops with hard-limited in-phase channel. Communi-

cations, IEEE Transactions on, 26(1):23–34.

Stensby, J. (1997). Phase-Locked Loops: Theory and Ap-

plications. Phase-locked Loops: Theory and Applica-

tions. Taylor & Francis.

Stensby, J. (2011). An exact formula for the half-plane pull-

in range of a PLL. Journal of the Franklin Institute,

348(4):671–684.

Suarez, A., Fernandez, E., Ramirez, F., and Sancho, S.

(2012). Stability and bifurcation analysis of self-

oscillating quasi-periodic regimes. IEEE Transactions

on microwave theory and techniques, 60(3):528–541.

Suarez, A. and Quere, R. (2003). Stability Analysis of Non-

linear Microwave Circuits. Artech House.

Thede, L. (2005). Practical analog and digital ﬁlter design.

Artech House.

Tranter, W., Bose, T., and Thamvichai, R. (2010). Ba-

sic Simulation Models of Phase Tracking Devices Us-

ing MATLAB. Synthesis lectures on communications.

Morgan & Claypool.

Vendelin, G., Pavio, A., and Rohde, U. (2005). Microwave

Circuit Design Using Linear and Nonlinear Tech-

niques. Wiley.

Wang, T.-C., Chiou, T.-Y., and Lall, S. (2008). Nonlinear

phase-locked loop design using semideﬁnite program-

ming. In 16th Mediterranean Conference on Control

and Automation, pages 1640–1645. IEEE.

Watada, K., Endo, T., and Seishi, H. (1998). Shilnikov

orbits in an autonomous third-order chaotic phase-

locked loop. IEEE transactions on circuits and

systems–I, 45(9):979–983.

Wiegand, C., Hedayat, C., and Hilleringmann, U. (2010).

Non-linear behaviour of charge-pump phase-locked

loops. Advances in Radio Science, 8:161–166.

Wu, N. (2002). Analog phaselock loop design using Popov

critereon. In Proceedings of the 2002 American Con-

trol Conference, volume 1, pages 16–18. IEEE.

Yoshimura, T., Iwade, S., Makino, H., and Matsuda, Y.

(2013). Analysis of pull-in range limit by charge

pump mismatch in a linear phase-locked loop. Cir-

cuits and Systems I: Regular Papers, IEEE Transac-

tions on, 60(4):896–907.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

710