Traffic Flow Simulation Dovetailed with Evolutionary Game Theory

Jun Tanimoto, Shinji Kukida, Aya Hagishima and Naoki Ikegaya

Interdisciplinary Graduate School of Engineering Sciences, Kyushu University, 6-1 Kasuga-koen,

Kasuga-shi, 816-8580, Japan

Keywords: Cellular Automaton, Traffic Flow, Lane Change, Dilemma Game, N-Person Prisoner’s Dilemma.

Abstract: Previous work (Yamauchi et al., PRE 79 and Nakata et al., Physica A 389) found several social-dilemma

structures in phases of traffic flows created by bottlenecks resulting from lane closings. We investigate

another question: whether or not such structures can be formed from frequent lane changes in a usual traffic

flow without any explicit bottlenecks. In our model system, two classes of driver-agents coexist: C-agents

(cooperative strategy) always remain in the lane they are initially assigned, while D-agents (defective

strategy) try to change lanes to move ahead. In relatively high-density flows, such as the metastable and

high-density phases, we found structures that correspond to either n-person Prisoner’s Dilemma (n-PD)

games or to quasi-PD games. In these situations, lane changes by D-agents create heavy traffic jams that

reduce social efficiency.

1 INTRODUCTION

In growing social concerns on traffic problems, there

have been lots of previous studies dealing with the

so-called traffic model (e.g. Kerner, 2009).

Especially, it has struck many statistical physicists

as interesting, just because a traffic flow can be

interrupted as a self-driven multi-particles system. In

that particular sense, among several traffic models

such as the kinetic gas theory, fluid dynamical

model, car-following model, cellular automaton

(CA) model has been most heavily concerned.

However, none of these previous studies provided a

comprehensive understanding on real traffic flow

phenomena because these models did not include the

decision-making process of the drivers. If we

recognize that the traffic flow results from

competition for a finite resource (“road”) among

many drivers who are seeking shorter driving times

and more comfortable driving, it is natural to ask

whether or not a social dilemma originates from the

intentions of drivers. If so, we question the class of

dilemma, such as the Prisoner’s Dilemma (PD)

game, Chicken (Snow Drift) game, or something

additional, lies hidden beneath the observed traffic

flow and performs the game change when the flow

changes from one kind of phase to another. With this

background, we detected that several social dilemma

structures, represented by n-person Prisoner’s

Dilemma (n-PD) games, appear in certain traffic

flow phases at a bottleneck caused by a lane closing

(Yamauchi et al., 2009; Nakata et al., 2010). We

confirmed that an n-PD game structure appears in

the high-density phase area, but no social dilemma

exists in the free-flow and jam phases. It seems

plausible for a social dilemma to underlie such

traffic flows because closing a lane creates an

obvious bottleneck. Thus, our next challenge is

whether a social dilemma still lies beneath traffic

flow that does not involve any explicit bottleneck

like a lane closing, on-ramp (merging), off-ramp

(exit), or uphill travel. This paper addresses whether

or not only lane-changing actions by drivers can

give rise to a social dilemma in an ordinal two-lane

road system with cyclic boundaries.

2 MODEL SETUP

We applied the Revised S-NFS model (Kokubo,

2011) for driving vehicles forward. Revised S-NFS

model takes into account motions that are commonly

observed in real vehicles: slow-to-start (S2S), quick

start (QS), and random braking (RB). S2S implies an

inertial effect, which is important for producing

metastable states in fundamental diagrams, also

improve reproducibility of the so-called three-phase

theory by Kerner (2009).

517

Tanimoto J., Kukida S., Hagishima A. and Ikegaya N..

Trafﬁc Flow Simulation Dovetailed with Evolutionary Game Theory.

DOI: 10.5220/0004986505170522

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2014),

pages 517-522

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

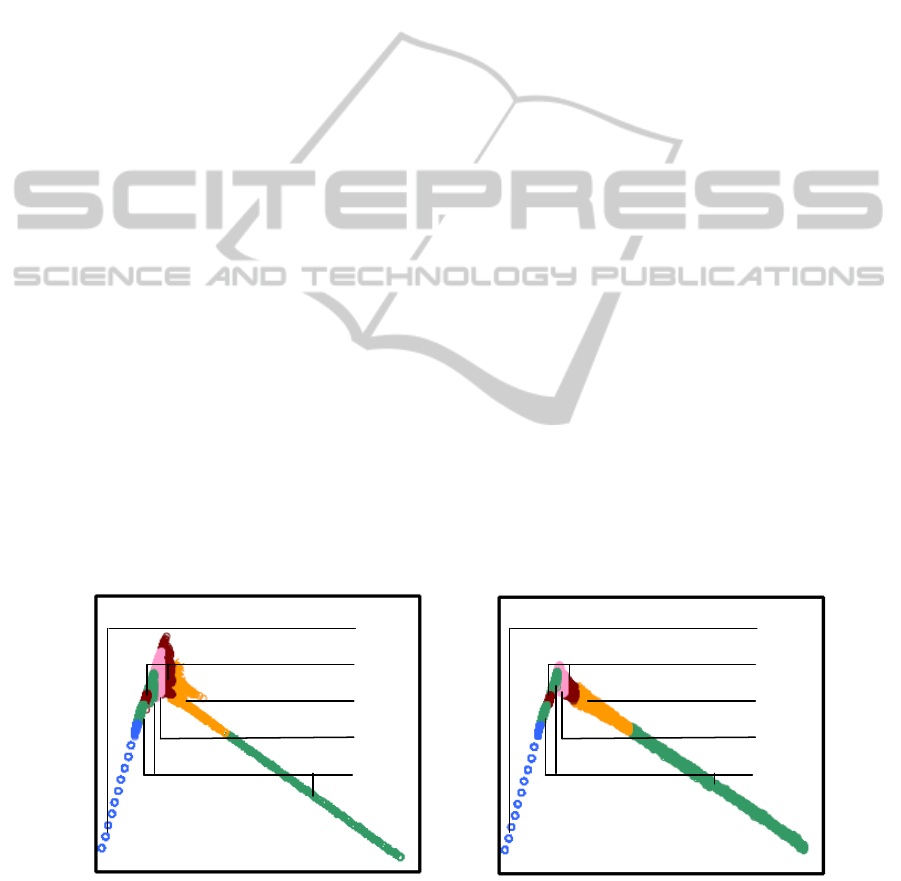
We applied the lane-changing rule used by

Kukida et al. (2009) in the CA model.

Concerning Revised S-NFS model and Kukida’s

lane change model, we assumed a set of model

parameters to reproduce realistic traffic flow. Also

we set the system length to L = 500.

In the system there are two types of agents:

cooperators (C-agents) remain in the lane initially

assigned without making any lane changes, and

defectors (D-agents) change lanes. We denote

fraction of cooperators among all agents by P

. We

use cyclic boundary conditions to keep the vehicle

density constant during a single simulation episode.

3 RESULT AND DISCUSSION

Figure 1 shows fundamental diagrams for (a) Pc = 1

and (b) Pc = 0 in which each dilemma class

discussed below is identified by a different color.

Figure 1(a) shows that flows of all cooperators can

exhibit the so-called metastable phase, while Figure

1(b) shows that no metastable phase occurs in flows

of all defectors. This seems plausible because a flow

in relatively high-density regions can be stable with

high traffic flux so long as none of the vehicles

change lanes. In contrast, a flow with lane changes

becomes volatile, since turbulence caused by

frequent lane changes promotes traffic jams.

Behaviors of the observed dilemma classes are

explicitly discussed below; here, we merely note that

only the Prisoner’s Dilemma (including quasi-PD

and quasi-little PD) class appears in the middle

density region with relatively high traffic fluxes. The

Trivial game and Neutral game also appear there,

but these are not categories of social dilemmas.

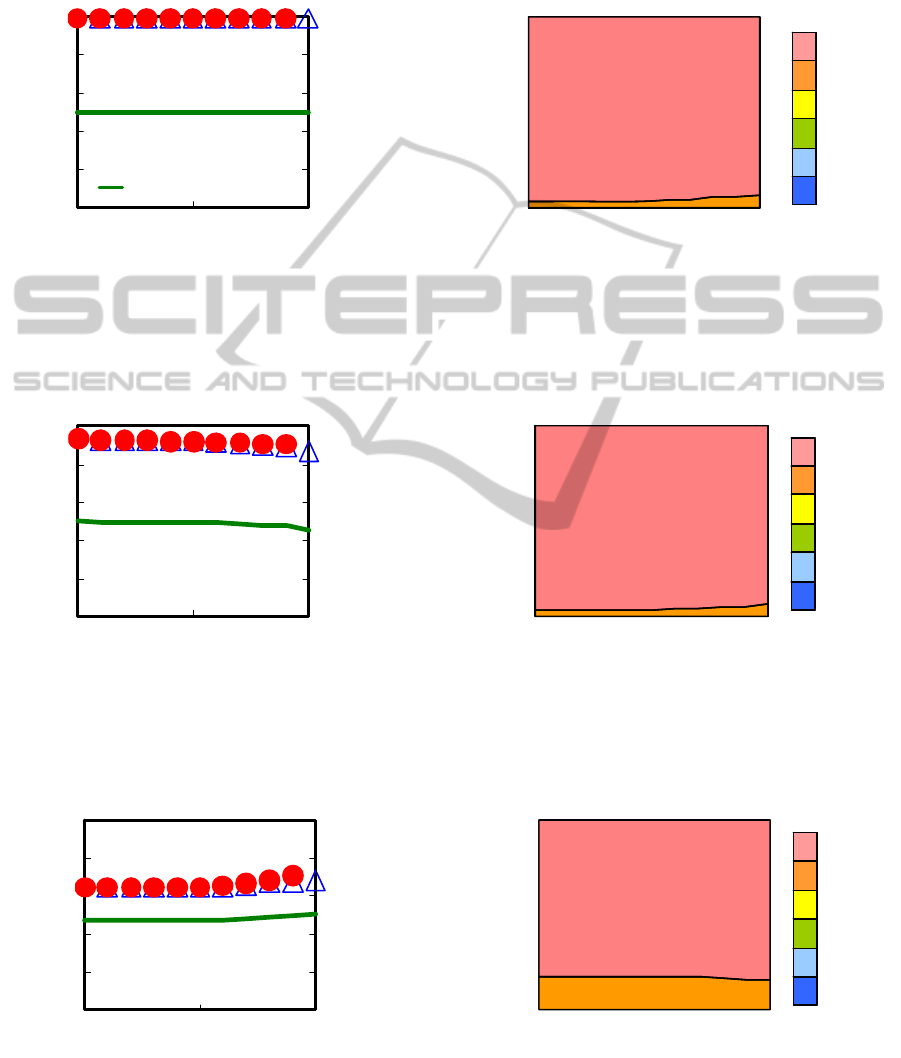
Figure 2 shows the payoff functions and velocity

frequencies for Case A in Figure 1(a) (

1.0





which is in the free-flow phase. Panel 2(a) shows

that all payoffs for Case A are insensitive to the

cooperation fraction; this implies a kind of gameless

situation. So we denote this as a Neutral game class.

This is not surprising because most of the vehicles in

Case A run at maximum velocity (see Panel 2(b)), so

lane changes in the system are rare.

Figures 3 to 9 show counterparts of Figure 2 for

the other cases explicitly marked in Figure 1(a). The

situation in Figure 3 (

141.0





) can be called a

Trivial game because Nash equilibrium (NE)

accords with the Equal Pareto Optimum (EPO) at P

= 0. This game is dominated by defection, since the

defector’s payoff is always larger than that of the

cooperator. However, the maximum social payoff

also appears at all defector states. In a nutshell, we

call this a D-dominate Trivial game, which implies

that more frequent lane changing is preferable in this

density region from both social and individual points

of view.

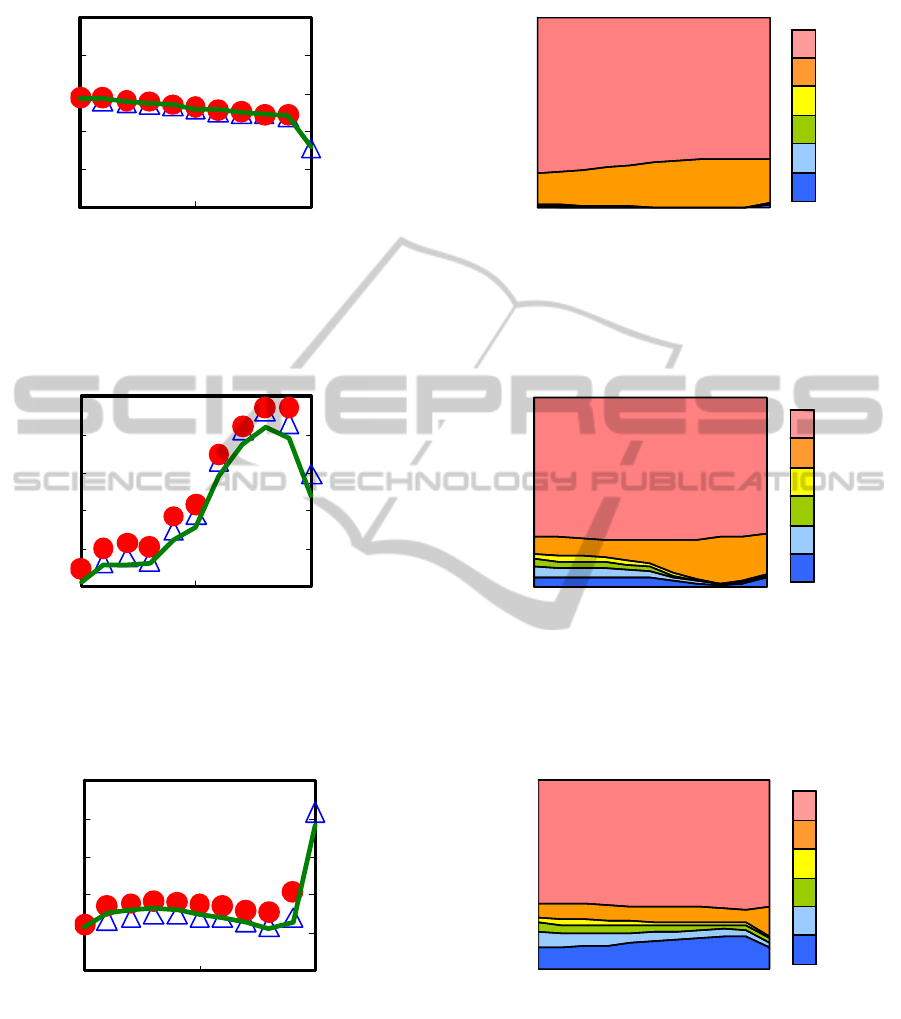
Figures 5 (

179.0





) and 9 (

6.0



) show the

same tendencies as in Figure 3. Thus, all these

should be classified as D-dominate Trivial games.

The fact that the jam phase belongs to the D-

dominate Trivial game (Fig. 9) seems reasonable

because lane changes into even a slightly small

vacant space between jamming vehicles brings

(b) P

1.2

Normalized density

(a) P

Normalized Flux

(A)

(B)

(E)

(C)

0.8

0.4

0.5 0.5

(D)

(A)

(B)

(E)

(C)

(D)

Figure 1: Fundamental diagrams (normalized flux vs normalized density) for situations with (a) all cooperators (P

= 1)

and (b) all defectors (P

=0). Colored symbols identify (A) Neutral game, (B) Prisoner’s Dilemma game at two densities

in Panels (a) and (b), (C) D-dominate Trivial game at three densities in Panels (a) and (b), (D) D-dominate quasi-PD

game, and (E) D-dominate quasi-light-PD game .

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

518

benefits for not only the focal vehicle who changes

lanes but also for the society as a whole, even if its

frequency is low.

Figure 4 (

155.0



) suggests a weak Prisoner’s

Dilemma (PD). This is confirmed by the following

facts. At P

= 0, NE is trapped because the defector’s

payoff is always greater than that of the cooperator.

EPO appears at P

= 1 because the social payoff

increases with increasing cooperation fraction,

although the effect is subtle. The same tendency

appears in Figure 7 (

211.0



), although the extent

of this dilemma seems more severe than that in

Figure 4. In Figure 7, the social payoff function does

not monotonically increase with the increase in the

cooperation fraction, as observed in Figure 4; rather,

it shows an N-character shape, in which a local peak

(much smaller than EPO at P

= 1) appears at a

lower cooperation fraction. This point is carefully

discussed in Sec. 3.2.

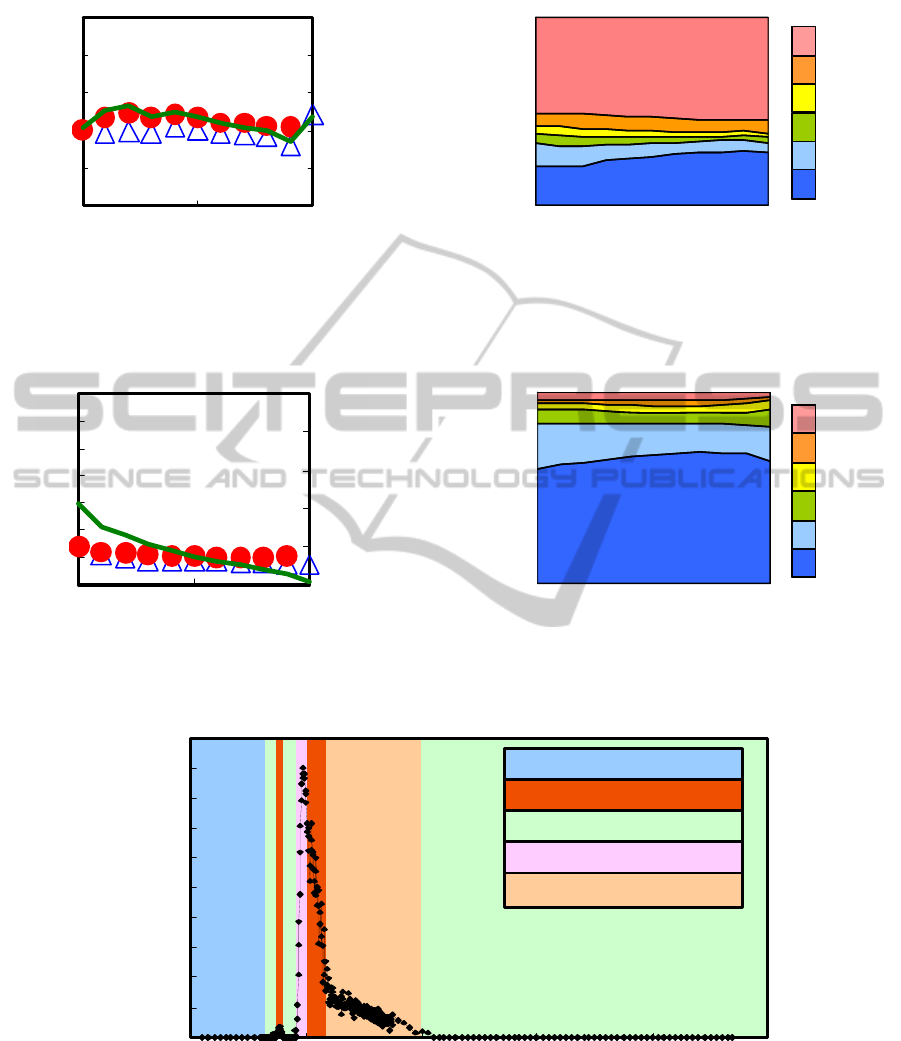
Figure 6 (

194.0



) differs slightly from the

simple PD because EPO is not observed at P

= 1,

although NE is trapped at P

= 0. At any rate, EPO is

largely inconsistent with NE since EPO, which is the

peak of social payoff, appears above P

= 0.5.

Therefore, we call this game structure a D-dominate

quasi-Prisoner’s Dilemma game.

Figure 8 (

244.0



) seems odd; it looks

analogous to a D-dominate quasi-PD Game (Fig. 6),

but it differs. EPO defined by the peak of social

payoff appears below P

= 0.5 and is relatively close

to NE found at P

= 0. Therefore, we call this a D-

dominate quasi-light PD game.

Figure 10 shows the effects of vehicle density on the

strength of dilemma,



, defined by Nakata et al.

(2011). Figure 10 shows that the density at severe

dilemma strength is consistent with the density

observed in the high-flux region, including the

metastable phase (Fig.1 (a)). This seems physically

plausible because, in this density region, a driver has

a strong incentive for changing lanes to exploit other

drivers and ensure his own benefit is maximized

(smaller travel time). However, when one driver

changes lanes, others might follow. Therefore, states

with high flux, say in the metastable phase, collapse

with the phase shifting to the jam phase.

4 CONCLUSIONS

For ordinal traffic flows, we have successfully

demonstrated that there are hidden social-dilemma

structures evoked by drivers’ decisions whether or

not they should change lanes. This was confirmed by

a series of numerical simulations using the revised

S-NFS cellular automaton model combined with a

lane-changing model that we developed and applied

with cyclic boundary conditions.

Interestingly, social dilemmas, as classified by

the Prisoner’s Dilemma game or its variants, were

only observed in situations of middle vehicle

density; these situations correspond to the region on

the fundamental diagram, including the metastable

phase, in which data are scattered. This seems

plausible because, when a driver is surrounded by

other vehicles, that driver has a serious incentive to

change lanes. However, if all drivers make the same

decision, social efficiency declines phenomenally

and huge traffic jams emerge. We also evaluated the

relation between dilemma strength and density of

vehicles.

ACKNOWLEDGEMENTS

This study was partially supported by a Grant-in-Aid

for Scientific Research by JSPS, awarded to Prof.

Tanimoto (#25560165), Pfizer Health Research

Foundation. We would like to express our gratitude

to these funding sources.

REFERENCES

Kerner, B. S, 2009; Introduction to Modern Traffic Flow

Theory and Control: The Long Road to Three-Phase

Traffic Theory, Springer.

Kokubo. S., Tanimoto. J., Hagishima. A., 2011; A new

Cellular Automata Model including a decelerating

damping effect to reproduce Kerner's three-phase

theory, Physica A 390(4), 561–568.

Kukida. S.; Tanimoto. J.; Hagishima. A., 2011; Analysis

of the influence of lane changing on traffic-flow

dynamics based on the cellular automaton model,

International Journal of Modern Physics C 22(3), 1–11.

Nakata, M., Yamauchi, A., Tanimoto, J., Hagishima, A.,

2010; Dilemma game structure hidden in traffic flow

at a bottleneck due to a 2 into 1 lane junction, Physica

A 389, 5353–5361.

Yamauchi, A., Tanimoto, J., Hagishima, A., Sagara, H.,

2009; Dilemma game structure observed in traffic

flow at a 2-to-1 lane junction, Physical Review E 79,

036104.

TrafficFlowSimulationDovetailedwithEvolutionaryGameTheory

519

APPENDIX

4.5

4.6

4.7

4.8

4.9

00.51

0.45

0.47

0.49

0.51

0.53

0.55

Normalized Velocit

Normalized flux

Velocity frequency

0.5 0 1

(a) Payoff functions (b) Velocity frequency

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

C-agent’s velocity

D-agent’s velocity

Flux

△

●

Figure 2: Results for

1.0



at point A in Figure 1(a). (a) Effect of fraction of cooperators (P

) on payoff functions

(velocity and flux). Red closed circles are average payoffs of defectors, and blue triangle are average payoffs of

cooperators. Green bold line indicates traffic flux as a social payoff. (b) Effect of fraction of cooperators (P

) on velocity

frequency. This behavior corresponds to a Neutral game.

4.5

4.6

4.7

4.8

4.9

00.51

0.65

0.67

0.69

0.71

0.73

0.75

Normalized Velocity

Normalized flux

0.5 0 1

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

0.141

Velocity frequency

Figure 3: Same as in Figure 2, except at

141.0



, which corresponds to one of the three points C in Figure 1(a). This

behavior corresponds to a D-dominate Trivial game.

4.5

4.6

4.7

4.8

4.9

00.51

0.7

0.72

0.74

0.76

0.78

0.8

Normalized Velocity

Normalized flux

Velocity frequency

0.5 0 1

(a) Payoff functions (b) Velocity frequency

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

0.155

Figure 4: Same as in Figure 2, except at

155.0



, which corresponds to one of the two points B in Figure 1(a). This

behavior corresponds to a weak Prisoner’s Dilemma game.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

520

4.5

4.6

4.7

4.8

4.9

00.51

0.8

0.82

0.84

0.86

0.88

0.9

Normalized Velocit

Normalized flux

Velocity frequency

0.5 0 1

(a) Payoff functions (b) Velocity frequency

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

0.179

Figure 5: Same as in Figure 2, except at

179.0



, which corresponds to one of the three points C in Figure 1(a). This

behavior corresponds to a D-dominate Trivial game.

4.2

4.3

4.4

4.5

4.6

4.7

00.51

0.82

0.84

0.86

0.88

0.9

0.92

Normalized Velocit

Normalized flux

Velocity frequency

0.5 0 1

(a) Payoff functions (b) Velocity frequency

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

0.194

Figure 6: Same as in Figure 2, except at

194.0





, which corresponds to point D in Figure 1(a). This behavior

corresponds to a D-dominate quasi-Prisoner’s Dilemma game.

3.7

3.8

3.9

4.1

4.2

00.51

0.78

0.8

0.82

0.84

0.86

0.88

Normalized Velocity

Normalized flux

Velocity frequency

0.5 0 1

(a) Payoff functions (b) Velocity frequency

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

0.211

Figure 7: Same as in Figure 2, except at

211.0



, which corresponds to one of the two points B in Figure 1(a). This

behavior corresponds to a weak Prisoner’s Dilemma game.

TrafficFlowSimulationDovetailedwithEvolutionaryGameTheory

521

3.1

3.2

3.3

3.4

3.5

00.51

0.73

0.75

0.77

0.79

0.81

0.83

Normalized Velocity

Normalized flux

Velocity frequency

0.5 0 1

(a) Payoff functions (b) Velocity frequency

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

0.244

Figure 8: Same as in Figure 2, except at

244.0





, which corresponds to point E in Figure 1(a). This behavior

corresponds to a D-dominate quasi-light PD game.

0.6

0.7

0.8

0.9

1.1

1.2

1.3

00.51

0.4

0.42

0.44

0.46

0.48

0.5

Normalized Velocity

Normalized flux

Velocity frequency

0.5 0 1

(a) Payoff functions (b) Velocity frequency

V=5

V=4

V=2

V=3

V=1

V=0

V=5

V=4

V=2

V=3

V=1

V=0

0.6

Figure 9: Same as in Figure 2, except at

6.0



, which corresponds to one of the three points C in Figure 1(a). This

behavior corresponds to a D-dominate Trivial game.

Normalized Density

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.1

00.20.40.60.81

D-dominate q-light PDG

D-dominate q-PDG

D-dominate Trivial Game

Neutral Game

Prisoner’s Dilemma Game

Figure 10: Effects of vehicle density on dilemma strength,



. Each color identifies one of the dilemma classses shown in

Figure 1(a): (A) Neutral game, (B) Prisoner’s Dilemma game, (C) D-dominate Trivial game, (D) D-dominate quasi-PD

game, and (E) D-dominate quasi-light-PD game.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

522