Afﬁne Invariant Shape Matching using Histogram of Radon Transform

and Angle Correlation Matrix

Makoto Hasegawa

and Salvatore Tabbone

Tokyo Denki University, 5 Senju Asahi-cho, Adachi-ku, Tokyo 120-8551 Japan

LORIA, UMR 7503, Universit

e de Lorraine, 54506 Vandoeuvre-l

es-Nancy, France

Keywords:

Shape Descriptor, Afﬁne Invariance, Radon Transform, Dynamic Time Warping Distance, Beam Search.

Abstract:

An afﬁne invariant shape matching descriptor using the histogram of Radon transform (HRT) and the dynamic

time warping (DTW) distance is proposed. Our descriptor based on the Radon transform is robust to shape

rotation, uniform scaling, and translation. For non-uniform scaling and shearing, our descriptor has a non-

linear sparse and dense distortion relative to the angle coordinates. Therefore, we apply DTW on a cost matrix

to be robust to these transformations. This cost matrix is deﬁned as an angle correlation matrix based on the

product of two matrices only. Moreover, based on the beam search algorithm, we speed-up the time complexity

of our method. Experimental results show that our approach is fast to compute and competitive compared to

well-known descriptors.

1 INTRODUCTION

Geometric invariant shape descriptors are very impor-

tant for shape recognition. Usually shape descriptors

need to be invariant to classical geometric transfor-

mations like rotation, scaling and translation. How-

ever these transformations are not enough in several

applications. Recently, a shape recognition applica-

tion using a portable digital camera has been pro-

posed in (Liang et al., 2005) where shapes (included

in the photos) are deformed following afﬁne distor-

tions. Therefore, it is necessary to be invariant to such

distortions.

RST invariant descriptors have been proposed for

shapes description and matching. Fourier transform

has been used as the starting point for the proposal of

many shape descriptors. The generic Fourier descrip-

tor (GFD) proposed by D. Zhang and G. Lu (Zhang

and Lu, 2002) is a typical one, and it is invariant to

rotation. However, in the case of translation and scal-

ing, GFD needs normalizations. The phase-only cor-

relation function (POC) proposed by C. Kuglin et al.

(D., 1975) has been shown to be effective for shape

matching. The Fourier–Mellin transform (FMT) pro-

posed by Chen et al. (Chen et al., 1994) is a typi-

cal Fourier descriptor invariant to RST transforma-

tions. Fourier descriptors have proved their robust-

ness to RST transformations and many applications

have been developed using these descriptors (Arafat

et al., 2009; Yuyama and Mitsuhashi, 2008; Ouyang

et al., 2006).

Many shape descriptors using the Radon trans-

form (Deans, 1993) have been deﬁned in the liter-

ature by Tabbone et al. (Tabbone et al., 2006). A

method called the histogram of Radon transform

(HRT) (Tabbone et al., 2008) has been proposed us-

ing the Radon transform and a two-dimensional his-

togram. This descriptor encodes the shape length

at each orientation; it is invariant to the shape scal-

ing and translation, and the shape rotation is pro-

jected to a horizontal translation on the domain.

Recently, the Amplitude-only log Radon transform

(ALR) (Hasegawa and Tabbone, 2012) has been de-

ﬁned. This descriptor is based on the Radon trans-

form, amplitude extraction, and log mapping. It is

invariant to shape translation; shape rotation and scal-

ing are projected into a two-dimensional translation.

To keep the invariance to these transformations (ro-

tation and scaling) the phase-only correlation func-

tion is used where the computation of several Fourier

transforms are needed. Combined with the DTW, this

descriptor is in addition invariant to any afﬁne distor-

tions. The reported results on recognition rates are

very good compared to the literature but the complex-

ity of the approach is very high. A method proposed

by K.C. et al. (Santosh et al., 2011) combined the

Radon transform and the dynamic time warping. The

authors apply directly the dynamic time warping to

Hasegawa M. and Tabbone S..

Afﬁne Invariant Shape Matching using Histogram of Radon Transform and Angle Correlation Matrix.

DOI: 10.5220/0004787000210029

In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 21-29

ISBN: 978-989-758-018-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

the radial coordinate in the Radon domain. The ap-

proach is invariant to the RST transformations also.

In the case of invariant methods to any afﬁne distor-

tions, the local descriptor ASIFT was proposed by

Morel and Yu (Morel and Yu, 2009). ASIFT is an

enhanced method of the conventional SIFT proposed

by Lowe (Lowe, 2004). Shape matching is performed

following local features detected into the images.

In this paper, we focus on a novel shape match-

ing and descriptor method robust to classical RST

(Rotation Scaling Translation) transformations and

to distortions especially for non-uniform scaling and

shearing. We propose a new method based on

HRT (Tabbone et al., 2008) . When a shape has

any non-linear transformations as shearing or non-

uniform scaling, we show that such non-linear shape

transformations become an only horizontal sparse and

dense distortion relative to the angular coordinates in

the HRT domain. In order to obtain invariance to

such horizontal distortions, we apply the DTW which

is one of the famous method for non-linear match-

ing. Our method is robust to not only RST trans-

formations (rotation, scaling, and translation), but

also non-linear shape transformations. Furthermore,

a fast computation method with the beam search al-

gorithm (Tillmann et al., 1997) is performed in our

DTW. Our previous method with ALR-DTW descrip-

tor needs the phase-only correlation to generate the

angle correlation matrix. Our new method with HRT

can generate the angle correlation matrix by a matrix

product only, so we provide a very fast computation.

The remainder of this paper is organized as fol-

lows. The Radon transform and the HRT descriptor

are recalled in Sections 2 and 3. Our shape match-

ing methods – including the descriptor matching, the

dynamic time warping method, and the beam search

method are discussed in Section 4. Experimental re-

sults are given in Section 5, and ﬁnally our conclu-

sions are drawn in Section 6.

2 RADON TRANSFORM

We recall the Radon transform deﬁnition in this sec-

tion. Let a coordinate (x, y) in the two-dimensional

x − y plane described as x, and an original image rep-

resented as f (x). The Radon transform of f (x) is de-

ﬁned as:

(θ, ρ) =

f (x)δ(x · ξ − ρ)dx, (1)

where ξ = (cos θ, sinθ), and δ(·) is a delta function.

In other words, the Radon transform is the integral of

f (x) over lines

θρ

= {x ∈ R

|x · ξ = ρ}, (2)

(a) (b) (c)

(d) (e) (f)

Figure 1: (a) Original image “Dog”. (b) RST transforma-

tion. (c) Shearing. (d) Non-uniform scaling. (e) Reﬂection.

(f) Original image “Hand”.

where ρ is the distance between the origin and L

θρ

, the

unit vector ξ and the angle θ describe the orientation

of the line L

θρ

. The line integral is computed by a

delta function δ(·).

The Radon transform has useful properties for the

RST transformations.

P1 Rotation : when shapes are rotated by θ

, the

Radon transform R

(θ, ρ) is translated to θ

rel-

ative to the coordinate θ as:

(θ, ρ) → R

(θ − θ

, ρ), (3)

where R

(θ, ρ) is cyclic for θ as:

(−θ, ρ) = R

(π − θ, ρ). (4)

P2 Scaling : when shapes are scaled by α, the Radon

transform R

(θ, ρ) is scaled by α relative to

the coordinate ρ. Moreover, the magnitude of

(θ, ρ) is multiplied by α as:

(θ, ρ) → αR



θ,



. (5)

P3 Translation : when shapes are translated to x

the Radon transform R

(θ, ρ) is translated to x

·ξ

relative to the coordinate ρ as:

(θ, ρ) → R

(θ, ρ − x

· ξ). (6)

The results of the Radon transform of Fig. 1 are

shown in Fig. 2.

3 HISTOGRAM OF RADON

TRANSFORM

3.1 Histogram

Let be f be a real function deﬁned on a domain X :

f : X → Y . Besides, let us denote by # the cardinality

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

Angle

Radius

0 20 40 60 80 100 120 140 160

−150

−100

−50

100

150

100

150

200

(a)

Angle

Radius

0 20 40 60 80 100 120 140 160

−150

−100

−50

100

150

(b)

Angle

Radius

0 20 40 60 80 100 120 140 160

−150

−100

−50

100

150

100

120

140

160

180

200

(c)

Angle

Radius

0 20 40 60 80 100 120 140 160

−150

−100

−50

100

150

100

120

140

160

180

200

(d)

Angle

Radius

0 20 40 60 80 100 120 140 160

−150

−100

−50

100

150

100

150

200

(e)

Angle

Radius

0 20 40 60 80 100 120 140 160

−150

−100

−50

100

150

100

150

200

(f)

Figure 2: The Radon transform of Figs. 1(a) – 1(f).

of a set and by |X| the size (length) of a domain X.

Hence, the point-wise histogram of f is expressed by:

H ( f )(v) =

#{x ∈ X|v = f (x)}

|X|

. (7)

By the normalization using |X| in Eq. (7), the his-

togram H ( f )(v) means a generation probability of v.

Actually, the range of v is quantized by N bins v

(1 ≤ i ≤ N) and, we put the data f (x) into the bins:

H ( f )(v

) =

#{x ∈ X| | f (x) − v

| <

}

|X|

, (8)

where #{.} means the number of items in a bin, and:

4 =

max f (x) − min f (x)

. (9)

The number of bins N is usually set by experience.

3.2 HRT Descriptor

The HRT descriptor is deﬁned as a matrix of frequen-

cies computed on the Radon transform for the angle

parameter (Tabbone et al., 2008). Thus, the HRT de-

scriptor represents a 2D histogram of shape lengths at

each orientation. More precisely, the HRT descriptor

is:

(θ, v) = H (R

(θ, ·))(v), (10)

with

(θ, ρ) →

(θ, ρ)

max

θ,ρ

(θ, ρ))

, (11)

where θ ∈ [0, π); v > 0, and X in Eq. (7) is:



ρ|R

(θ, ρ) > 0



(12)

so that the generation probability of histograms is in-

variant to the shape scaling.

The HRT descriptor has beneﬁcial properties as:

P4 Rotation: when shapes are rotated by θ

, the HRT

descriptor is translated to θ

relative to the coor-

dinate θ as:

(θ, v) → D

(θ − θ

, v), (13)

where D(θ, v) is cyclic for the θ as:

(−θ, v) = D

(π − θ, v). (14)

AffineInvariantShapeMatchingusingHistogramofRadonTransformandAngleCorrelationMatrix

(a) (b)

(e) (f)

Figure 3: Our HRT for Figs. 1(a) – 1(f).

P5 Scaling and Translation: when shapes are scaled

or translated, the HRT descriptor is invariant.

P6 Non-linear Distortion: when shapes get non-

linear distortions as shearing or non-uniform scal-

ing, the HRT descriptor gets sparse and dense dis-

tortion, only horizontally, on the transform do-

main.

Let’s consider for instance Fig. 1(c). This ﬁgure

is a slanted version (θ = 30

◦

) of Fig. 1(a). Following

the Radon transform, the integral of f (x) over verti-

cal lines (θ = 90

◦

) on Fig. 1(a) are equal to the case

of Fig. 1(c). On the other hand, the integral of f (x)

over horizontal lines (θ = 0

◦

) on Fig. 1(a) are dif-

ferent from the slant lines on Fig. 1(c). As a result,

some columns on the domain remain the same and

some columns are translated horizontally. This result

makes the horizontal sparse and dense distortion on

the domain. Therefore, in order to obtain invariance to

non-linear horizontal distortions, we apply the DTW

for the non-linear matching.

The HRT descriptors of the original shapes in

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

100

150

200

250

300

350

400

450

500

550

600

(a)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

100

150

200

250

300

350

400

450

500

550

600

(b)

Figure 4: (a) The cost matrix for the HRT images shown in

Figs. 3(a) and 3(c). (b) The normalized warping path.

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

Figs. 1(a)–1(f) are shown in Fig. 3 (where the num-

ber of bins N = 256). In the case of the RST trans-

formations shown in Fig. 1(b), our descriptor shown

in Fig. 3(b) is only translated horizontally for the

shape rotation. Our descriptor is invariant to the shape

scaling and translation. In the case of shearing and

non-uniform scaling as shown in Figs. 1(c) and 1(d),

our descriptor (see Figs. 3(c) and 3(d)) has horizontal

sparse and dense distortions. In the case of reﬂection

shown in Fig. 1(e), our descriptor (see Fig. 3(e)) is re-

ﬂected in the angle coordinate. For a different shape

shown in Fig. 1(f), our descriptor in Fig. 3(f) is differ-

ent from Fig. 3(a).

4 SHAPE MATCHING

4.1 Angle Correlation Matrix

Since our descriptor is computed with discrete values,

it can be described using a matrix as:

(θ, v) → D

θ,v

, (15)

where θ is digitized with integers 1 ∼ 180, and v is the

bin number. Therefore, the size of D

θ,v

is 180 × N.

Two descriptors one for the query and the other for

the template are denoted as Q

θ,v

and T

θ,v

Our angle correlation matrix M

i, j

is computed as:

i, j

= Q

j,v

× T

i,v

, (16)

where i and j are respectively the template and the

query angle; the size of M

i, j

is 180 × 180. Q

means

a transposition of a matrix Q. A cost matrix C

i, j

computed using the angle correlation matrix M

i, j

as:

i, j

. (17)

A cost matrix C

i, j

is shown in Fig. 4(a). A val-

ley line (in black in the ﬁgure) called “warping path”

appears in C

i, j

, when the two shapes are same even

if they have RST transformations or any afﬁne distor-

tions.

The warping path is denoted as:

P = p

, p

, ·· · , p

, (18)

where p

is a coordinate (i

, j

) on C

i, j

, p

= (1, 1),

= (180, 180), and 180 ≤ K < 360. We normalize

i, j

periodically so that the position with the mini-

mum value in C

i, j

becomes (1, 1). If the minimum

value in C

i, j

is not unique, the minimum value on the

most upper-left on the image is chosen. Fig. 4(b) is

the result of the normalized warping path.

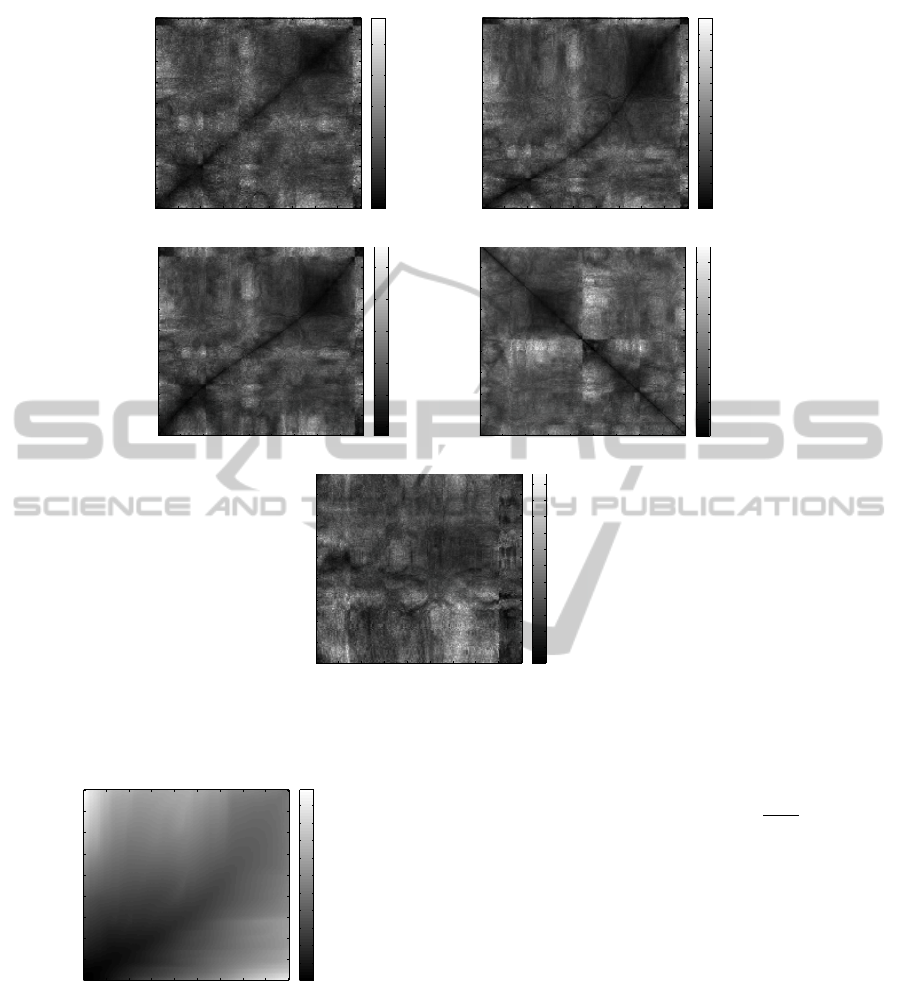
Cost matrices shown in Figs. 5(a) – 5(e) are cases

using the query shown in Fig. 3(a) and templates

shown in Figs. 3(b) – 3(f), respectively. For only RST

transformations (see Fig. 5(a)), a straight valley line

appears in the domain. In the case of shearing and

non-uniform scaling shown in Figs. 5(b) and 5(c), a

curved valley line appears in each case. A cost matrix

for shapes which are different as shown in Fig. 5(e)

has no valley line.

In the case of the shape reﬂection, the Radon im-

age and HRT image are reﬂected following the angu-

lar coordinate as shown in Figs. 2(e) and 3(e). Since

the corresponding angle order is reversed, the cost

matrix C

i, j

is set as: C

i, j

← C

i,181− j

. In this case, the

cost matrix show (see Fig. 5(d)) a straight valley line

with negative slope due to the reﬂection property of

the Radon transform.

4.2 Dynamic Time Warping (DTW)

Our dynamic time warping is performed using an ac-

cumulated cost matrix A

i, j

to search the minimum

cost as:

i, j

= C

i, j

+ min

(m,n)

m,n

(m, n) ∈

{

(i − 1, j),(i, j − 1), (i − 1, j − 1)

}

, (19)

where A

1, j

= C

1, j

+ A

1, j−1

; A

i,1

= C

i,1

+ A

i−1,1

;

1,1

= C

1,1

. Therefore, Eq. (19) tracks the warping

path. An accumulated cost matrix A

i, j

is shown in

Fig. 6.

We track back the warping path p

= (i

, j

) from

= (180, 180) to p

= (1, 1) as:

k−1

= arg min

(m,n)

m,n

(m, n) ∈

{

− 1, j

), (i

, j

− 1), (i

− 1, j

− 1)

}

(20)

The matching score between two shapes is com-

puted using the path length K as:

S =

180,180

. (21)

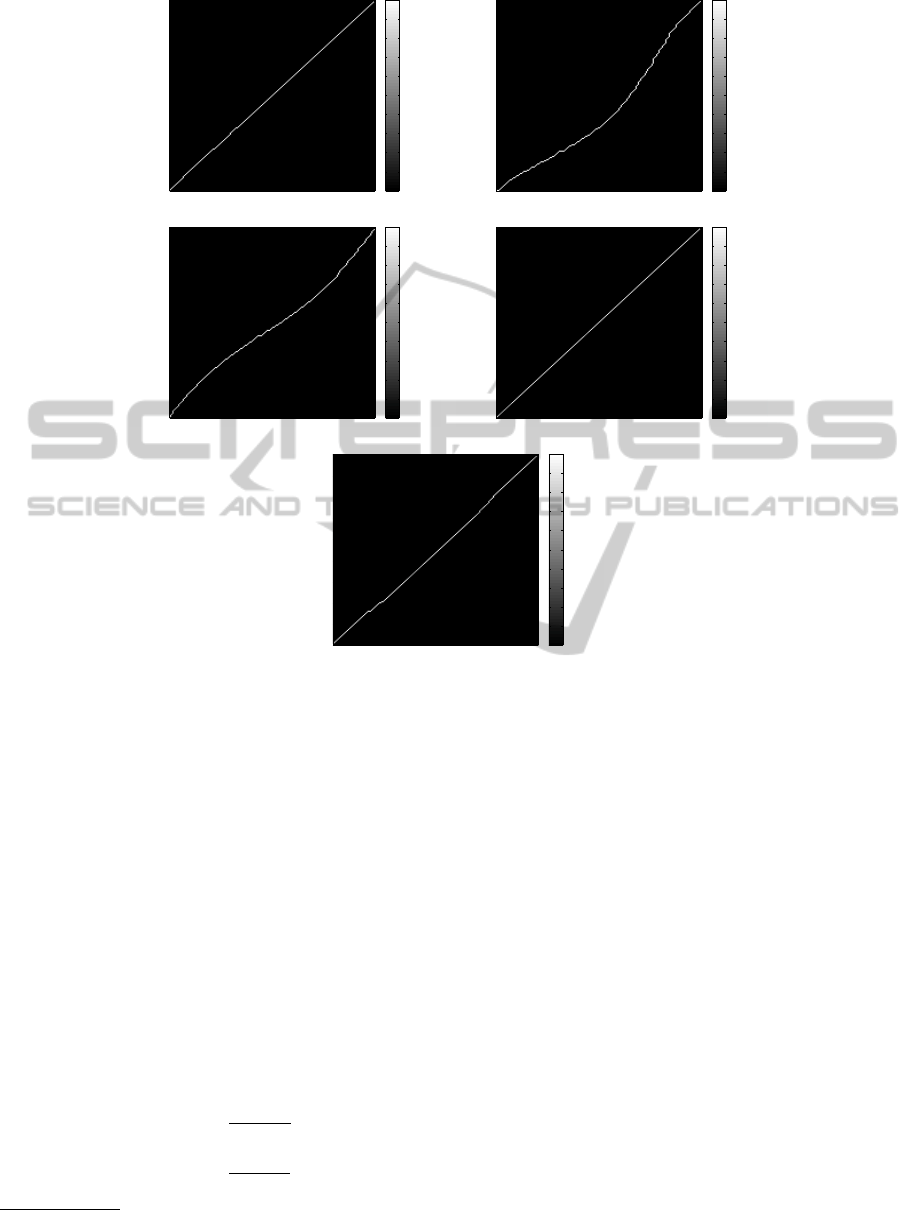
Warping paths shown in Figs. 7(a) – 7(e) are the

case using a query shown in Fig. 3(a) and templates

shown in Figs. 3(b) – 3(f), respectively. A warping

path under the RST transformations shown in Fig.

7(a) is a straight line. In the case of shearing and non-

uniform scaling shown in Figs. 7(b) and 7(c), their

warping paths are curved lines. In the case of re-

ﬂection and matching with different shapes (see Figs.

7(d) and 7(e)), their corresponding warping paths are

also straight lines.

AffineInvariantShapeMatchingusingHistogramofRadonTransformandAngleCorrelationMatrix

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

100

200

300

400

500

600

(a)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

100

150

200

250

300

350

400

450

500

550

600

(b)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

100

200

300

400

500

600

(c)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

100

150

200

250

300

350

400

450

500

550

(d)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

150

200

250

300

350

400

450

500

550

600

650

(e)

Figure 5: Cost matrices: (a) – (e) are the cases with a query shown in Fig. 3(a) and templates shown in Figs. 3(b) – 3(f),

respectively.

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.5

1.5

2.5

3.5

4.5

x 10

Figure 6: The accumulated cost matrix of Fig. 4(b).

4.3 Beam Search

The beam search(Tillmann et al., 1997) is a

fast computation algorithm for the DTW. Our

beam search skips A

i, j

computation in Eq.

(19), when A

i−1, j

> T

i−1, j

, A

i, j−1

> T

i, j−1

, and

i−1, j−1

> T

i−1, j−1

i, j

is initialized to ∞ at the

ﬁrst), where:

i, j

= T

min

+ (T

max

− T

min

) ×

i + j

360

. (22)

min

and T

max

are thresholds for the beam band. It

means a pruning searching tree deﬁned by Eq. (19).

An accumulated cost matrix without the beam

search is shown in Fig. 8(a). Its warping paths is

denoted using a black line. The result of the beam

search, an accumulated cost matrix within thresholds

min

= 1000 and T

max

= 30000 is shown in Fig. 8(b).

A search band is generated, and the computation for

the accumulated cost matrix is reduced. We can re-

mark that the warping path is included in the search

band.

5 EXPERIMENTAL RESULTS

To demonstrate the performance of our descriptor,

we have carried out experiments based on commonly

used binary datasets. An afﬁne distorted shape dataset

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(a)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(b)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(c)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(d)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(e)

Figure 7: Warping paths: (a) – (e) are the cases with a query shown in Fig. 3(a) and templates shown in Figs. 3(b) – 3(f),

respectively.

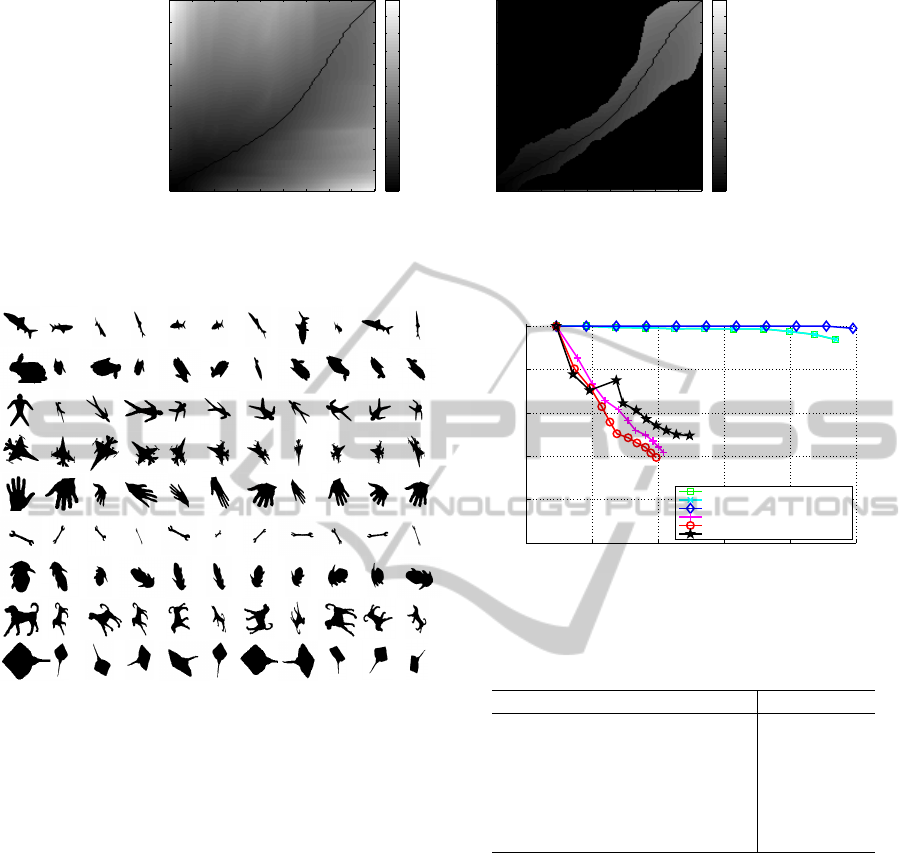
shown in Fig. 9 consists of 9 categories with afﬁne

distortions (99 images). These datasets are created

from a commonly used dataset in many works and is

available from the research community

Our method (HRT-DTW) is computed with and

without the beam search algorithm; ALR with the

dynamic time warping (ALR-DTW) (Hasegawa and

Tabbone, 2012), HRT (Tabbone et al., 2008), FMT

(Chen et al., 1994), and ASIFT (Morel and Yu, 2009).

In the case of ASIFT, we use an source code provided

by Morel and Yu on their web site

The performance is evaluated using the precision-

recall measure (Davis and Goadrich, 2006) deﬁned

as:

Precision =

t p

t p + f p

Recall =

t p

t p + f n

, (23)

http://www.lems.brown.edu/vision/researchAreas/SIID/

http://www.cmap.polytechnique.fr/ yu/

where the true positives t p is the number of items

correctly labeled as belonging to the positive class,

the false positives f p is the number of items incor-

rectly labeled as belonging to the class, and the false

negatives f n is the number of items which were not

labeled as belonging to the positive class but should

have been. Namely, the precision is the number of

true positives divided by the total number of elements

labeled as belonging to the positive class. The recall is

the number of true positive divided by the total num-

ber of elements that actually belong to the positive

class. We create a precision-recall curve by plotting

Precision and Recall at each retrieval rate.

Precision-recall curves of each method is shown

in Fig. 10. Our method and ALR-DTW are very simi-

lar and have very high performances compared to the

other. Both descriptors are robust to any afﬁne distor-

tions. Moreover, we can remark no decrease with the

beam search algorithm.

The processing time to match two images for dif-

ferent methods is shown in Table 1 using Intel Core

AffineInvariantShapeMatchingusingHistogramofRadonTransformandAngleCorrelationMatrix

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.5

1.5

2.5

3.5

4.5

x 10

(a)

Query Angle

Template Angle

20 40 60 80 100 120 140 160 180

100

120

140

160

180

0.5

1.5

2.5

3.5

4.5

x 10

(b)

Figure 8: (a) The accumulated cost matrix; (b) the result of the beam search with the thresholds T

min

= 1000 and T

max

= 30000.

The warping paths are denoted with black lines.

Figure 9: An afﬁne distorted dataset. This dataset has 9

categories with afﬁne distortions.

i7-366U 2.00 GHz CPU. ASIFT is implemented in C,

and the other methods are implemented using MAT-

LAB. HRT and FMT are very fast, however they are

not robust to any afﬁne distortions. Comparing with

ALR-DTW, our processing time is about one tenth

compared to ALR-DTW. It is observed that the com-

puting of the angle correlation matrix by a matrix

product in Eq. (16) provides very fast computation

and the processing time using our beam search algo-

rithm is signiﬁcant (about one half less time compared

to HRT-DTW).

6 CONCLUSIONS

We propose a new method based on the HRT descrip-

tor. The HRT descriptor is robust to shape scaling,

translation and rotation. However, for non-uniform

shape scaling and shearing, this descriptor has a non-

linear sparse and dense distortions relative to the an-

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Recall

Precision

HRT-DTW

HRT-DTW with beam search

ALR-DTW

HRT

FMT

ASIFT

Figure 10: Precision-recall curves of each method.

Table 1: Processing time for the matching between two im-

ages.

Method Time [Sec.]

HRT-DTW 0.43

HRT-DTW(with beam search) 0.27

ALR-DTW 4.03

HRT 0.01

FMT 0.01

ASIFT 11.97

gle coordinates. Therefore, we propose a novel afﬁne

invariant shape matching combining HRT with the

DTW. DTW is set on a cost matrix deﬁned as an angle

correlation matrix based on the product of two matri-

ces only. The computational complexity is reduced

using the beam search algorithm. Reported results on

a common dataset have shown a very good robust-

ness to any afﬁne transformations with low complex-

ity time thanks to the angle correlation matrix product

and the beam search algorithm.

In order to keep our approach scalable, future

works will be devoted to optimize the value of the pa-

rameters related to the size of the histogram (number

of bins) and the Radon transform (number of orienta-

tions).

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

REFERENCES

Arafat, S. Y., Saleem, M., and Hussain, S. A. (2009). Com-

parative analysis of invariant schemes for logo classi-

ﬁcation. International Conference on Emerging Tech-

nologies, pages 256–261.

Chen, Q.-S., Defrise, M., and Deconinck, F. (1994). Sym-

metric phase-only matched ﬁltering of Fourier-Mellin

transforms for image registration and recognition.

IEEE Trans. Pattern Anal. Mach. Intell., 16(12):1156–

1168.

D., K. C. (1975). The phase correlation image alignment

methed. Proc. Int. Conference Cybernetics Society,

pages 163–165.

Davis, J. and Goadrich, M. (2006). The relationship be-

tween precision-recall and roc curves. In Proceed-

ings of the 23rd international conference on Machine

learning, ICML ’06, pages 233–240, New York, NY,

USA. ACM.

Deans, S. R. (1993). The Radon Transform and Some of Its

Applications. Krieger Publishing Company.

Hasegawa, M. and Tabbone, S. (2012). Afﬁne invariant

shape matching using Radon transform and dynamic

time warping distance. In ACM Symposium On Ap-

plied Computing (ACM SAC), Trento.

Liang, J., Doermann, D., and Li, H. (2005). Camera–based

analysis of text and documents: a survey. Interna-

tional Journal on Document Analysis and Recogni-

tion, 7(2 – 3):83 – 104.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Morel, J.-M. and Yu, G. (2009). ASIFT: A new framework

for fully afﬁne invariant image comparison. SIAM J.

Imaging Sciences, 2(2):438–469.

Ouyang, Z., Feng, J., Su, F., and Cai, A. (2006). Fingerprint

matching with rotation-descriptor texture features. In

ICPR (4), pages 417–420. IEEE Computer Society.

Santosh, K. C., Lamiroy, B., and Wendling, L. (2011).

DTW for matching Radon features: A pattern recogni-

tion and retrieval method. In ACIVS, pages 249–260.

Tabbone, S., Terrades, O. R., and Barrat, S. (2008). His-

togram of Radon transform. a useful descriptor for

shape retrieval. In ICPR, pages 1–4. IEEE.

Tabbone, S., Wendling, L., and Salmon, J.-P. (2006). A

new shape descriptor deﬁned on the Radon trans-

form. Computer Vision and Image Understanding,

102(1):42–51.

Tillmann, C., Vogel, S., Ney, H., Zubiaga, A., and Sawaf,

H. (1997). Accelerated dp based search for statisti-

cal translation. In Kokkinakis, G., Fakotakis, N., and

Dermatas, E., editors, EUROSPEECH. ISCA.

Yuyama, J. and Mitsuhashi, W. (2008). Shape invariant

recognition of polygonal road signs by deforming ref-

erence templates. ICSPCS, pages 1–6.

Zhang, D. and Lu, G. (2002). Shape-based image retrieval

using generic Fourier descriptor. Sig. Proc.: Image

Comm., 17(10):825–848.

AffineInvariantShapeMatchingusingHistogramofRadonTransformandAngleCorrelationMatrix