
Analysis of MIMO Systems with Transmitter-side Antennas Correlation
Francisco Cano-Broncano
1
, C´esar Benavente-Peces
1
, Andreas Ahrens
2
,
Francisco Javier Ortega-Gonz´alez
1
and Jos´e Manuel Pardo-Mart´ın
1
1
Universidad Polit´ecnica de Madrid, Ctra. Valencia. km. 7, 28031 Madrid, Spain
2
Hochschule Wismar, University of Technology, Business and Design, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany
Keywords:
Multiple Input Multiple Output, Antennas Correlation, Wireless Communication.
Abstract:
Due to its potential performance multiple input multiple output (MIMO) systems are being included in the
current standard developments. Nevertheless issues like antennas proximity at the transmitter and receiver
arrays can limit the achievable performance. Antennas proximity produces a phenomenon called correlation
which affects the channel performance by reducing the capacity and increasing the BER. Hence, the aim of
this paper is investigating the transmitter-side antennas correlation modelling and effects. Together with the
appropriate signal processing (e. g. singular values decomposition), the effect of transmitter-side antennas
correlation is studied. Our results show that under the effect of antennas correlation not necessarily all layers
might be used for the data transmission since the weighting of the stronger layer within the MIMO system
becomes even stronger respect to non-correlated channels. Simulation results are shown to underline these
effects.
1 INTRODUCTION
Multiple Input Multiple Output (MIMO) systems
have been studied during the last decades due to their
ability to increase the channel capacity and decrease
the bit error rate (BER) without increasing the trans-
mit power needed at the transmitter side. In order to
obtain the full advantages of the MIMO systems per-
fect channel state information is required at both the
transmitter and receiver sides in order to perform the
appropriate signal processing tasks at the transmit-
ter (pre-processing) as well as at the receiver (post-
processing) side. A popular technique used for those
signal processing operations is the singular values de-
composition (SVD). By introducing both operations
inter-antenna interferences are avoided and the full
MIMO system capabilities can be exploited assuming
a highly scattered environment. Due to the antennas
physical proximity compared to the wavelength addi-
tional effects must be taken into consideration in the
analysis and implementation of a MIMO system. Un-
der that condition antennas correlation effect appears
affecting the MIMO channel capacity and (bit-error
rate) BER. MIMO systems require a highly scattered
environment in order to benefit from the use of multi-
ple antennas to select the appropriate transmit and re-
ceive conditions. This is synonymous of having mul-
tiple paths which largely differ.
Unfortunately, due to the proximity of the an-
tennas separation the theoretically degree of design-
freedom of the MIMO system decreases (Lee, 1973;
Ertel et al., 1998; Wang et al., 2009). In the pres-
ence of antennas correlation the environment is less
scattered and hence the MIMO channel capacity de-
creases and the BER rises. Antennas correlation im-
plies the similarity in the antennas paths and in conse-
quence the environment becomes less scattered. This
means that the off-diagonal elements of the channel
matrix become similar and it is not possible to exploit
the full capabilities of the MIMO system any longer.
In order to predict the effects of antenna correlation
a proper correlation model is required. The effect of
antennas correlation can be separated into two inde-
pendent effects: the one corresponding to transmitter-
side antennas correlation and that due to receiver-side
antennas correlation. In order to analyse and pre-
dict the behaviour of a correlated MIMO system two
key points must be solved: The first one concerns the
model of the antennas correlation (i. e. the description
of the correlation coefficients) and the second one is
related to analysing the correlation effect compared to
an uncorrelated MIMO system.
The antennas correlation is usually described by
the antennas correlation matrices one for transmitter-
side and other for receiver-side (assuming indepen-
dence between correlations) which collect the cor-
147
Cano-Broncano F., Benavente-Peces C., Ahrens A., Ortega-González F. and Pardo-Martín J..
Analysis of MIMO Systems with Transmitter-side Antennas Correlation.
DOI: 10.5220/0004228401470155
In Proceedings of the 3rd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2013), pages 147-155
ISBN: 978-989-8565-43-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

relation coefficients between the antennas, while the
global effect is represented by a called system corre-
lation matrix which is the Kronecker product (Laub,
2005) between the transmitter and receiver side an-
tennas correlation matrices (Taparugssanagorn et al.,
2006; Salz and Winters, 1994; Shiu et al., 2000).
In (Yueyu and Lili, 2007) the antennas correlation
effect on the channel capacity is studied when using a
circular array compared to a linear one showing the
decrease in the channel capacity with the antennas
correlation effect.
This paper is aimed at the analysis of MIMO sys-
tems performance in the presence of transmitter-side
antennas correlation. The main contribution of this
paper is the definition of the correlation coefficients
between transmitter-side antennas as a function of the
main parameters showing how they affects the char-
acteristic of the layer-specific weighting factors.
In this paper linear antennas arrays are studied.
The authors do not focus on concrete spatial antennas
distributions. Instead they use a general propagation
model in order to compute the correlation coefficient
between antennas.
The remaining part of this contribution is orga-
nized as follows: Section 2 describes the physical an-
tennas adjustment as well as the corresponding vari-
ables that will impact the computation of the anten-
nas correlation. The corresponding correlated MIMO
system model is introduced in Section 3. The associ-
ated performance results are presented and interpreted
in section 4. Finally, in section 5 the concluding re-
marks are discussed.
2 BASE-STATION RELATED
ANTENNAS CORRELATION
This section describes the physical antennas adjust-
ment as well as the corresponding variables that will
impact the computation of the antennas correlation.
Starting with the analysis of the correlation between
any pair of transmit antennas with respect to a given
receive antenna, the result will be extended to any an-
tennas configuration as the correlation is computed
for each antennas pair separately. At first, only line of
sight (LOS) trajectories are considered as highlighted
in Fig. 1.
Fig. 1 represents the physical set-up for a pair of
transmit antennas and one receive antenna. The dis-
tance between the receive antenna and the reference
point (centre of the physical disposition) of the trans-
mit antennas is D. The distance between the transmit
antenna #1 and the receive antenna is d
1
, while the
distance between the transmit antenna #2 and the re-
D
d
1
d
2
d/2
?
d/2
antenna #1
antenna #2
φ
α
1
α
2
Figure 1: Antennas’ physical disposition: two transmit and
one receive antennas.
ceive antenna is d
2
. The transmit antennas itself are
separated by the distance d. Considering the spac-
ings and angles introduced in Fig. 1 some relations
can be stated for each transmit antenna. Considering
transmit antenna #1, the following relation can be es-
tablished:
d
1
·cos(α
1
) = D−
d
2
·cos(φ) . (1)
Equation (1) describes the relation among the various
physical parameters described in Fig. 1. A similar re-
lation can be obtained for transmit antenna #2 dealing
with the following relation:
d
2
·cos(α
2
) = D+
d
2
·cos(φ) . (2)
Now, the focus is set on the computation of the corre-
lation between transmit antennas. Here, the antennas
set-up shown in Fig. 1 is considered. Let’s assume
that the same signal s(t) is simultaneously transmitted
through the transmit antennas #1 and #2. Under this
conditions the signals arriving at the receive antenna
can be described as follows: The signal arriving at the
receive antenna from transmit antenna #1 is given by:
s
r1
(t) = s(t) ·G
1
·A(d
1
) ·e
−j2πd
1
/λ
, (3)
where G
1
describes the transmit antenna #1 radia-
tion pattern gain in the direction of departure and
A(d
1
) ≤ 1 describes the path attenuation effect (given
in terms of gain) for the distance d
1
. The complex
exponential in (3) introduces the phase change suf-
fered by the signal from the transmit antenna #1 to
the receive antenna. The signal arriving at the receive
antenna from transmit antenna #2 is given by:
s
r2
(t) = s(t) ·G
2
·A(d
2
) ·e
−j2πd
2
/λ
. (4)
where G
2
describes the transmit antenna #2 radia-
tion pattern gain in the direction of departure and
A(d
2
) ≤ 1 describes the path attenuation effect for the
distance d
2
. Given D >> d it can be assumed that
A(d
1
) ≈ A(d
2
). The antennas correlation coefficient
(path correlation) is given by the correlation between
received signal s
r1
(t) and s
r2
(t) and can be expressed
PECCS2013-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
148

as follows:
ρ =
E{s
r1
(t) ·s
∗
r2
(t)}−E{s
r1
(t)}·E{s
r2
(t)}
p
E{s
r1
(t) ·s
∗
r1
(t)}·
p
E{s
r2
(t) ·s
∗
r2
(t)}
(5)
which can be rewritten as:
ρ =
E{s
r1
(t) ·s
∗
r2
(t)}
p
E{|s
r1
(t)|
2
}·
p
E{|s
r2
(t)|
2
}
(6)
under the assumption that the transmitted signal s(t)
is zero mean and hence s
r1
(t) and s
r2
(t) are zero mean
valued variables, too. In consequence, the expression
E{s
r1
(t) s
∗
r2
(t)} results in
E{s
r1
(t) ·s
∗
r2
(t)} = E{|s(t)|
2
}·G
1
·A(d
1
) ·G
2
·
A(d
2
) ·e
−j2π(d
1
−d
2
)/λ
. (7)
In order to simplify the analysis described above, fur-
ther assumptions should be considered: First, it is
assumed that the transmit signal s(t) is unitary, i.e.,
E{|s(t)|
2
} = 1 . Additionally it is assumed that the
transmit and receive antennas are isotropic with uni-
tary gain, i.e., G
1
= G
2
= 1 . Furthermore, given
D >> d and d
1
≈ d
2
then A(d
1
) ≈ A(d
2
) ≈ A(D) can
be concluded. Under these conditions equation (7)
can be reduced to:
E{s
r1
(t) ·s
∗
r2
(t)} = A
2
(D) ·e
−j2π(d
1
−d
2
)/λ
. (8)
Concerning the terms in the denominator in (6) the
same assumptions are applied obtaining:
E{s
r1
(t) ·s
∗
r1
(t)} = E{|s(t)|
2
}·G
2
1
·A
2
(d
1
)
= A
2
(d
1
) ≈ A
2
(D) (9)
and
E{s
r2
(t) ·s
∗
r2
(t)} = E{|s(t)|
2
}·G
2
2
·A
2
(d
2
)
= A
2
(d
2
) ≈ A
2
(D) . (10)
Finally, substituting (8), (9) and (10) in (6) the anten-
nas correlation coefficient can be expressed as:
ρ = e
−
j2π(d
1
−d
2
)
λ
. (11)
In order to rearrange equation (11) as a function of
those parameters described in Fig. 1, equations (2)
and (3) should be taken into consideration to com-
pute the distance difference d
1
−d
2
which should take
into account the phase difference between the signals
received from each transmit antenna. The difference
between (2) and (1) can be expressed as
d
2
·cos(α
2
) −d
1
·cos(α
1
) = d ·cos(φ) . (12)
Considering that the separation between transmit and
receive antenna is large enough compared to the sep-
aration between the transmit antennas, i. e., D >> d
then it can be assumed that α
1
≈ α
2
≈ ψ/2, where ψ
is called the spread angle. In consequence (12) can
be expressed as:
(d
2
−d
1
) ·cos(ψ/2) = d ·cos(φ) . (13)
Substituting the result in (13) into (11) the following
expression is obtained:
ρ = e
−j2πd cos(φ)
λ cos(ψ/2)
= e
−j2πd
λ
cos(φ)
cos(ψ/2)
, (14)
where d
λ
= d/λ is the transmit antennas separation
given in wavelengths units. Equation (14) reveals that
the transmit antennas path correlation coefficients de-
pends on the antennas separation d
λ
, the spread angle
ψ and the transmit antennas reference axe rotation an-
gle φ (or signals angle of departure). Assuming a far
field communication the term cos(ψ/2) in (13) can be
approximated to unity (assuming ψ is close to zero).
Under this assumption, the correlation coefficient re-
sults in:
ρ = e
−j2πd
λ
cos(φ)
. (15)
Up to now, the antennas correlation coefficient con-
centrates only on the line of sight (LOS) trajectories.
However, wireless channels requires scattered envi-
ronments to be taken into consideration. In scattered
environments the signals transmitted by the transmit
antennas are radiated and bounce in multiples obsta-
cles producing multipath signals which arrive at the
receive aerial in various arrival directions. In this case
the result obtained in (14) must be extended to such
scattered environments. Besides, the scatter departs
from the transmit antenna with random angles and
hence (13) can be extended to the scattered environ-
ment case as follows:
(d
2
−d
1
) ≈ d cos(φ+ ξ
i
) (16)
where ξ
i
states for the random variable modelling the
angles for the various scatters. Fig. 2 represents the
antennas disposition with the scatters representation,
where ξ
1ν
and ξ
2ν
refer to scatter ν for transmit an-
tenna #1 and scatter ν for transmit antenna #2 re-
spectively. The signals arriving at the receive antenna
D
d
1
d
2
d/2
f
x
1n
x
2n
d/2
antenna #1
antenna #2
Tx Rx
Figure 2: Antennas’ physical disposition: two transmit and
one receive antennas in a scattered environment.
from each transmit antenna must be appropriately sta-
tistically modeled in order to obtain a proper model.
AnalysisofMIMOSystemswithTransmitter-sideAntennasCorrelation
149
Considering equation (14), assuming far field com-
munication conditions and substituting (16) into (14)
the correlation coefficient becomes:
ρ = E{e
−
j2πd cos(φ+ξ
i
)
λ
}= E{ e
−j2πd
λ
cos(φ+ξ
i
)
} , (17)
where ξ
i
represents the arriving scatter angle devia-
tion from the shortest angle (that corresponds to the
LOS when feasible) and d
λ
= d/λ is the antennas
separation in wavelengths. The computation of the
expectation in (17) is given by:
ρ(φ,ξ) =
∞
Z
−∞
e
−j2πd
λ
cos(φ+ξ)
p(ξ)dξ , (18)
where p(ξ) is the probability distribution function
(pdf) of the scatters’ angles ξ
i
described previously.
An appropriate pdf should be defined for the random
variable ξ, also called spread angle. It is reasonable
to assume that scatters most concentrate around the
mean of the scatters angles. In consequence a normal
distribution with mean µ = 0 and variance σ
2
ξ
looks
appropriate for this purpose. Under this assumption,
the pdf can be expressed as
p(ξ) =
1
√
2πσ
ξ
e
−
ξ
2
2σ
2
ξ
. (19)
This model considers that most of the scatters concen-
trate around the shorter distance one and the probabil-
ity of having scatters with large spread angles is low.
Analysing (18) and (19), the term cos(φ + ξ) in (18)
can be developed as:
cos(φ+ ξ) = cos(φ) cos(ξ) −sin(φ) sin(ξ) . (20)
In the case ξ is small enough, i. e., cos(ξ) ≈ 1 and
sin(ξ) ≈ ξ, (20) can be approximated by:
cos(φ+ ξ) = cos(φ) −ξ sin(φ) . (21)
Substituting (21) into (18) leads to:
ρ(φ,ξ) =
∞
Z
−∞
e
−j2πd
λ
(cos(φ)−ξ sin(φ))
p(ξ)dξ , (22)
where the complex exponential can be separated as
the product of two terms, one that doesn’t depend on
ξ and hence (22) can be rewritten as:
ρ(φ,ξ) = e
−j2πd
λ
cos(φ)
∞
Z
−∞
e
−j2πd
λ
ξ sin(φ)
p(ξ)dξ .
(23)
Taken under consideration that:
∞
Z
−∞
e
−
1
2
a·x
2
+jbx
dx =
2π
a
(1/2)
·e
−
b
2
2a
(24)
0 5 10 15 20
0
0.2
0.4
0.6
0.8
1
A2
A1
case1XX
case2
case3
Figure 3: Dependency of |ρ(φ,σ
ξ
)| as a function of σ
ξ
and
φ assuming an antennas separation in wavelengths of d
λ
=
1/32.
0 5 10 15 20
0
0.2
0.4
0.6
0.8
1
|ρ(φ,σ
ξ
)| →
σ
ξ
→
φ = 30
◦
φ = 60
◦
φ = 90
◦
Figure 4: Dependency of |ρ(φ,σ
ξ
)|as a function of σ
ξ
and φ
assuming a wavelength specific antenna separation of d
λ
=
1/16.
and identifying b = 2πd
λ
sin(φ) and a = 1/σ
2
ξ
, finally
(23) becomes
ρ(φ,σ
ξ
) = e
−j2πd
λ
cos(φ)
e
−
1
2
(2πd
λ
sin(φ)σ
ξ
)
2
. (25)
Equation (25) allows determining the complex cor-
relation coefficient for a pair of antennas. This re-
sult can be extended to multiple antennas and various
space antennas distributions.
Fig. 3 depicts the modulus of the correlation co-
efficient for an antennas separation d
λ
= 1/32 (wave-
lengths) for various departure angles as a function of
the spread angle standard deviation σ
ξ
. For a given
departure angle, the correlation coefficient modulus
increases as the spread angle decreases. A lower value
of σ
ξ
means that the scatters concentrate in a narrower
space and the correlation increases. On the other
hand, for a given spread angle, the correlation coef-
ficient modulus decreases with the departure angle.
Fig. 4 and 5 represent the correlation coefficient mod-
ulus for d
λ
= 1/16 and d
λ
= 1/8 respectively. The
PECCS2013-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
150
0 5 10 15 20
0
0.2
0.4
0.6
0.8
1
|ρ(φ,σ
ξ
)| →
σ
ξ
→
φ = 30
◦
φ = 60
◦
φ = 90
◦
Figure 5: Dependency of |ρ(φ, σ
ξ
)|as a function of σ
ξ
and φ
assuming a wavelength specific antenna separation of d
λ
=
1/8.
effects of the departure angle and spread angle on the
correlation coefficient are the same as those described
in Fig. 3. Now, comparing Fig. 3–5 the effect of an-
tennas separation can be analysed. It can be noticed
that for the same spread angle and the same departure
angle the correlation coefficient modulus increases as
the antennas become closer.
3 MIMO SYSTEM MODEL
It is quite common to assume that the coefficients of
the (n
R
×n
T
) channel matrix H are independent and
Rayleigh distributed with equal variance. However,in
many cases correlations between the transmit anten-
nas as well as between the receive antennas can’t be
neglected. The way to include the antenna signal cor-
relation into the MIMO channel model with n
T
trans-
mit and n
R
receive antennas for Rayleigh flat-fading
like channels is given by (Oestges, 2006) and results
in
vec(H) = R
1
2
HH
·vec(G) (26)
where G is a (n
R
× n
T
) uncorrelated channel ma-
trix with independent, identically distributed com-
plex Rayleigh distributed elements and vec(·) be-
ing the operator stacking the matrix G into a vec-
tor column-wise. The matrix R
HH
describing the
correlation within the channel coefficients h
ν,µ
(with
ν = 1,. ..,n
R
and µ = 1,.. .,n
T
) is defined as
R
HH
= E
vec(H) ·vec(H)
H
(27)
with vec(H) resulting exemplarily for the considered
(2×2) MIMO system in
vec(H) =
h
1,1
h
2,1
h
1,2
h
2,2
. (28)
Assuming that the correlation introduced by the an-
tenna elements at the transmitter side is independent
from the correlation introduced by the antenna ele-
ments at the receiver side, the correlation matrix can
be defined over the transmitter side correlation ma-
trix R
TX
as well as the receiverside correlation matrix
R
RX
. In this case the matrix R
HH
results in
R
HH
= R
TX
⊗R
RX
(29)
where ⊗ represents the Kronecker product.
For the exemplarily investigated (2 × 2) MIMO
system, the transmitter side correlation matrix R
TX
is
given by
R
(2×2)
TX
=
ρ
(TX)
1,1
ρ
(TX)
1,2
ρ
(TX)
2,1
ρ
(TX)
2,2
!
=
1 ρ
(TX)
ρ
∗(TX)
1
(30)
and describes the correlation between the transmit an-
tennas k and ℓ, independent from the receive antenna
m. The transmitter side correlation coefficient be-
tween the transmit antennas k and ℓ is obtained as
ρ
(TX)
k,ℓ
= E{h
m,k
·h
∗
m,ℓ
} (31)
It should be taking under consideration that the value
of the correlation coefficient depends on the reference
antenna. That is, the correlation coefficient between
antenna ℓ and antenna k is given by:
ρ
(TX)
ℓ,k
= E{h
m,ℓ
·h
∗
m,k
} = ρ
∗(TX)
k,ℓ
. (32)
Hence in the correlation matrix the symmetric ele-
ments with respect the main diagonal are complex
conjugated. This relationship is due to the sign
change when computing the distance difference be-
tween antennas with different antenna reference.
In this work it is assumed that no correlation be-
tween the antennas at the receiverside appears. Under
this assumption the receiver side correlation matrix
R
RX
results in
R
(2×2)
RX
=
ρ
(RX)
1,1
ρ
(RX)
1,2
ρ
(RX)
2,1
ρ
(RX)
2,2
!
=
1 0
0 1
(33)
The receiver side correlation matrix R
RX
describes
the correlation between the receive antennas m and
n, independent from the receive antenna k. The re-
ceiver side correlation coefficient between the receive
antennas m and n can be calculated as follows
ρ
(RX)
m,n
= E{h
m,k
·h
∗
n,k
} . (34)
Finally, the overall correlation matrix R
HH
with the
elements
R
(2×2)
HH
=
ρ
1,1,1,1
ρ
1,1,1,2
ρ
1,2,1,1
ρ
1,2,1,2
ρ
1,1,2,1
ρ
1,1,2,2
ρ
1,2,2,1
ρ
1,2,2,2
ρ
2,1,1,1
ρ
2,1,1,2
ρ
2,2,1,1
ρ
2,2,1,2
ρ
2,1,2,1
ρ
2,1,2,2
ρ
2,2,2,1
ρ
2,2,2,2
(35)
AnalysisofMIMOSystemswithTransmitter-sideAntennasCorrelation
151
results in
R
(2×2)
HH
=
1 0 ρ
(TX)
0
0 1 0 ρ
(TX)
ρ
∗(TX)
0 1 0
0 ρ
∗(TX)
0 1
.
(36)
Therein, the elements ρ
m,n,k,ℓ
of the overall correla-
tion matrix R
HH
are given by the following equation
ρ
m,n,k,ℓ
= E{h
m,k
·h
∗
n,ℓ
} = ρ
(TX)
k,ℓ
·ρ
(RX)
m,n
. (37)
When considering a non-frequency selective SDM
(space division multiplexing) MIMO link composed
of n
T
transmit and n
R
receive antennas, the system is
modelled by
u = H·c+ w . (38)
In (38), u is the (n
R
×1) received vector, c is the
(n
T
×1) transmitted signal vector containing the com-
plex input symbols and w is the (n
R
×1) vector of the
additive, white Gaussian noise (AWGN). The inter-
ference between the different antenna’s data streams,
which is introduced by the non-diagonal channel ma-
trix H, requires appropriate signal processing strate-
gies. Common strategies for separating the data
streams are linear equalization at the receiver side or
linear pre-equalization at the transmitter side, if chan-
nel state information is available. Unfortunately, lin-
ear equalization suffers from noise enhancement and
linear pre-equalization of the transmit signal from an
increase in the transmit power. Both schemes only of-
fer poor power efficiency. Therefore, other signal pro-
cessing strategies have attracted a lot of interest. An-
other popular technique is based on the singular value
decomposition (SVD) (Haykin, 2002) of the system
matrix H, which can be written as H = S · V · D
H
,
where S and D
H
are unitary matrices and V is a real-
valued diagonal matrix of the positive square roots of
the eigenvalues of the matrix H
H
H sorted in descend-
ing order
1
. The SDM MIMO data vector c is now
multiplied by the matrix D before transmission. In
turn, the receiver multiplies the received vector u by
the matrix S
H
. Thereby neither the transmit power nor
the noise power are enhanced. The overall transmis-
sion relationship is defined as
y = S
H
(H·D·c+ w) = V·c+ ˜w. (39)
Here, the channel matrix H is transformed into inde-
pendent, non-interfering layers having unequal gains.
When applying the proposed system structure, the
SVD-based equalization leads to different weighted
AWGN channels, where the weighting factor
p
ξ
ℓ,k
1
The transpose and conjugate transpose (Hermitian) of
D are denoted by D
T
and D
H
, respectively.
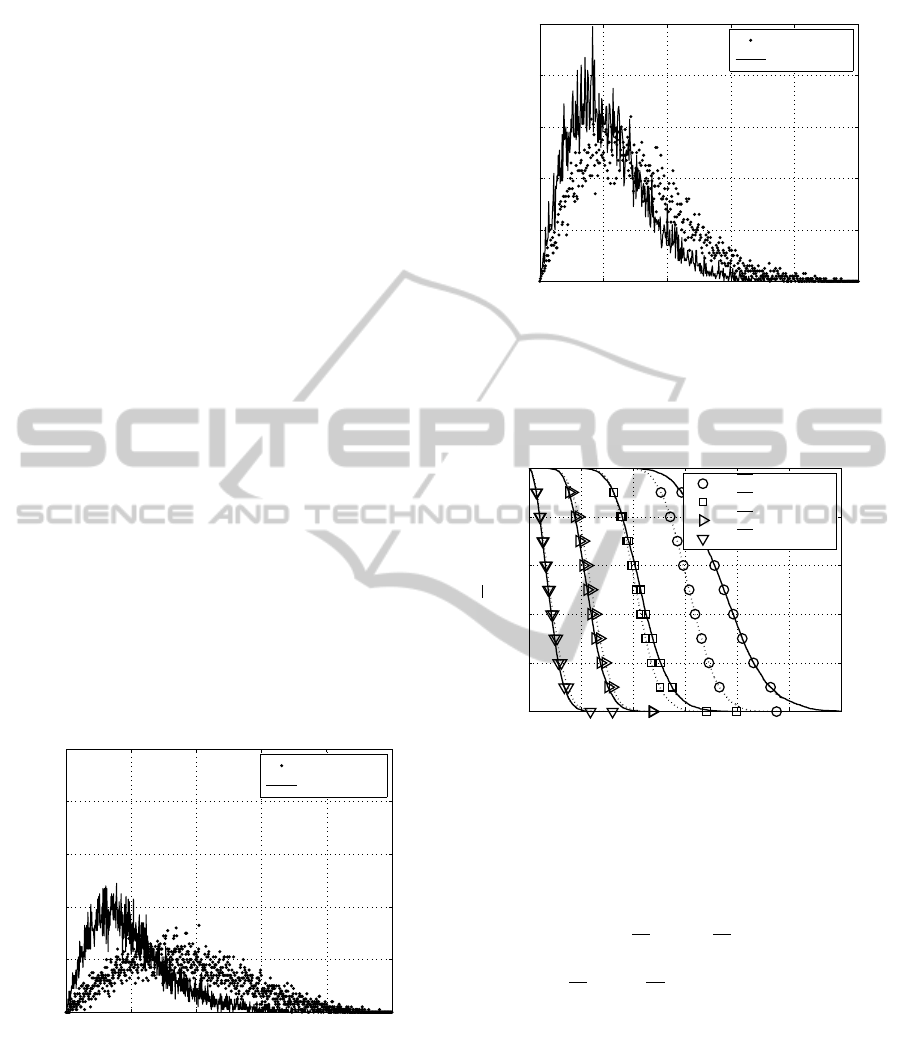
c
ℓ,k
y
ℓ,k
˜w
ℓ,k
p
ξ
ℓ,k
Figure 6: Resulting system model per MIMO layer ℓ and
transmitted data block k.
represents the positive square roots of the eigenval-
ues of the matrix H
H
H for the transmitted SDM data
block k (Fig. 6). The number of readily separable lay-
ers is limited by min(n
T
,n
R
).
4 RESULTS
For the performance analysis two different MIMO
configurations are studied: Within the (2×2) MIMO
system, the transmitter-side correlation matrix R
TX
is given according to (30), whereas in the (4 ×4)
MIMO system it is assumed that correlation appears
only between neighbouring antennas. The four anten-
nas at the transmitter side are linearly disposed and
uniformly distributed with a separation of d
λ
. Fig. 7
shows the physical layout of the transmit antennas
with respect to one of the receive antennas where an-
tennas are numbered in increasing order. The discus-
sion developed below can be applied to any receive
antenna.
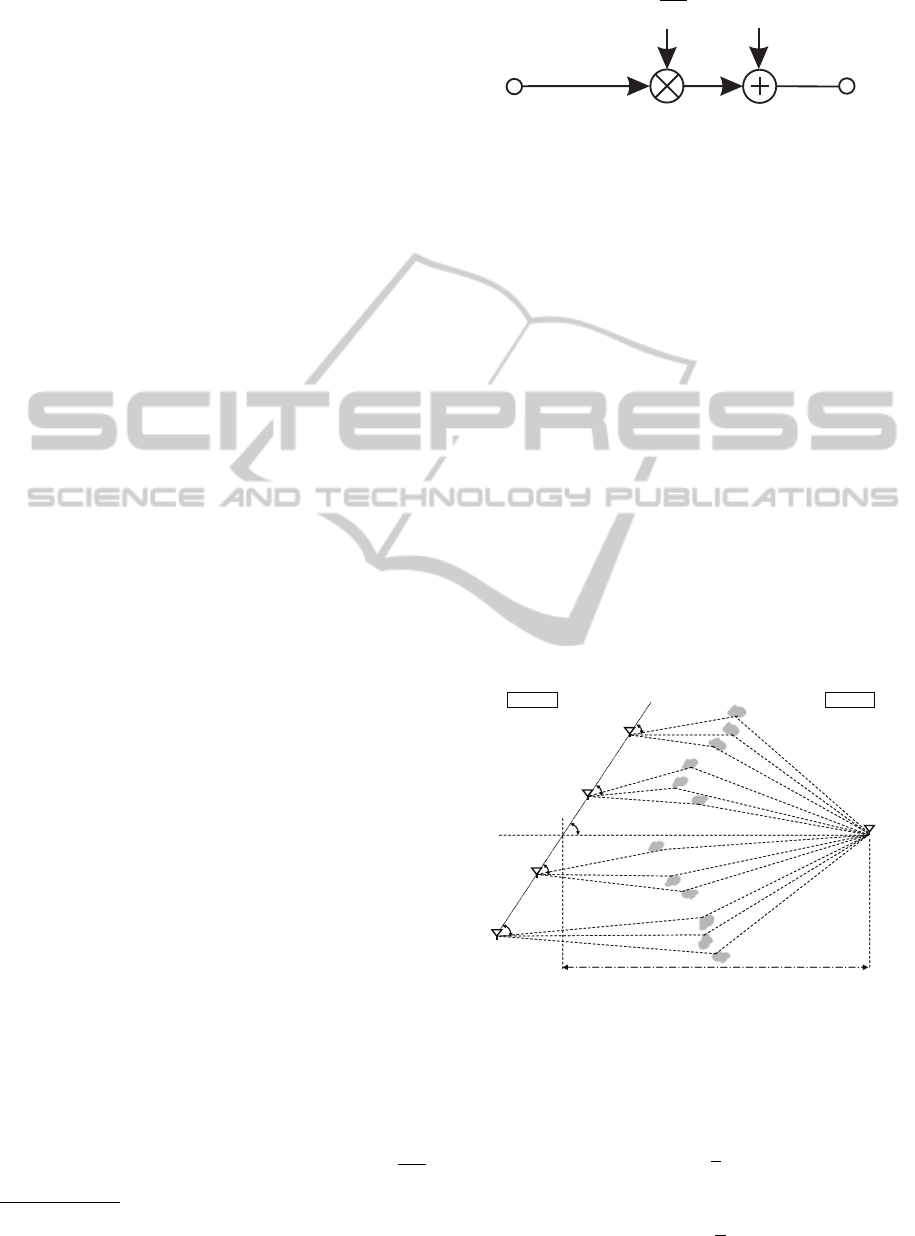
D
d
1
d
2
d
f
x
1n
x
2n
d
antenna #1
antenna #2
Tx Rx
antenna #1
antenna #3
antenna #4
d
3
d
4
x
3n
x
4n
d
Figure 7: Antennas’ physical disposition: (4 ×4) MIMO
with neighbour transmit antennas correlation.
From Fig. 7 various equations can be obtained for
each pair of transmit antennas. For antennas #1 and
#2 and the antennas physical layout it is obtained:
d
1
·cos(α
1
) = D−
3
2
d ·cos(φ) (40)
and
d
2
·cos(α
2
) = D−
d
2
·cos(φ) . (41)
PECCS2013-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
152

By combining (40) and (41) the following relation is
obtained:
d
2
·cos(α
2
) −d
1
·cos(α
1
) = d ·cos(φ) . (42)
For neighbour antennas #2 and #3 it is obtained equa-
tion (41) and:
d
3
·cos(α
3
) = D+
d
2
·cos(φ). (43)
By combining (41) and (43) the following relation is
obtained:
d
3
·cos(α
3
) −d
2
·cos(α
2
) = d ·cos(φ) . (44)
Finally, for neighbour antennas #3 and #4 it is ob-
tained equation (43) and:
d
4
·cos(α
3
) = D+
3
2
d ·cos(φ) . (45)
Finally, in a similar way than in previous antennas
pairs, by combining (43) and (45) the following re-
lation is obtained:
d
4
·cos(α
4
) −d
3
·cos(α
3
) = d ·cos(φ) . (46)
Once the physical description and relations of the an-
tennas layout has been described the next step is com-
puting the neighbour antennas correlation following
the steps described in the (2×2) MIMO set-up. Con-
sidering the separation between transmit and receive
antennas is large compared with the transmit anten-
nas separation, i.e., D >> d then it can be assumed
that α
1
≈ α
2
≈ α
3
≈ α
4
≈ ψ/4 where ψ is called the
spread angle. In consequence (42), (44) and (46) can
be respectively expressed as:
(d
2
−d
1
) ·cos(ψ/4) = d ·cos(φ) , (47)
(d
3
−d
2
) ·cos(ψ/4) = d ·cos(φ) , (48)
and
(d
4
−d
3
) ·cos(ψ/4) = d ·cos(φ) . (49)
Furthermore, if D >> d then cos(ψ/4) ≈ 1 and the
equations above can be further simplified. Let’s con-
sider antennas #1 and #2. The correlation coefficient
is given according to (6) by:
ρ
(TX)
12
=
E{s
r1
(t) ·s
∗
r2
(t)}
p
E{|s
r1
(t)|
2
}·
p
E{|s
r2
(t)|
2
}
. (50)
where s
r1
(t) and s
r2
(t) are the signals received from
antennas #1 and #2 respectively. The received signals
covariance, e. g. E{s
r1
(t) ·s
∗
r2
(t)} is given by
E{s
r1
(t) ·s
∗
r2
(t)} = A
2
(D) ·e
−j2π(d
1
−d
2
)/λ
. (51)
where it was considered that d
1
≈ d
2
≈ D and hence
A(d
1
) ≈A(d
2
) ≈A(D). Besides it was considered that
antennas are isotropic with unity gain. The signals
standard deviations are given respectively by
q
E{|s
r1
(t)|
2
} =
q
A
2
(d
1
) ·G
2
1
= A(D) (52)
and
q
E{|s
r2
(t)|
2
} =
q
A
2
(d
2
) ·G
2
2
= A(D) . (53)
It was assumed that the same signal s(t) is a zero mean
unitary power signal and it was transmitted from each
transmit antenna signal and hence s
r1
(t) and s
r2
(t) are
zero mean valued variables. Substituting (51), (52)
and (53) in (50) it is finally obtained:
ρ
(TX)
12
=
A
2
(D) ·e
−
j2π(d
1
−d
2
)
λ
A
2
(D)
= e
−
j2π(d
1
−d
2
)
λ
. (54)
The result obtained in (54) can be extended to any
pair of neighbour antennas. Finally, considering the
result in equations (47), (48) and (49), the correlation
coefficients between neighbourantennas are given by:
ρ
(TX)
12
= ρ
(TX)
23
= ρ
(TX)
34
= e
−j2πd
λ
·cos(φ)
cos(ψ/4)
. (55)
where d
λ
= d/λ is the antennas separation in wave-
length units. Further simplifications in can be per-
formed considering that in practice D >> d and fi-
nally cos(ψ/4) ≈ 1. By assuming a far field commu-
nication, the term (i. e. cos(ψ/4) can be approximated
to unity assuming ψ is close to zero). Under this as-
sumption, the correlation coefficients result in:
ρ
(TX)
12
= ρ
(TX)
23
= ρ
(TX)
34
= e
−j2πd
λ
cos(φ)
. (56)
The transmit antennas correlation matrix is then given
by:
R
(4×4)
TX
=
1 ρ
(TX)
12
0 0
ρ
(TX)
21
1 ρ
(TX)
23
0
0 ρ
(TX)
32
1 ρ
(TX)
34
0 0 ρ
(TX)
43
1
.
(57)
The obtained results are so far focussed on line-of-
sight propagation. However, wireless channels re-
quire scattering conditions to be taken into consider-
ation. Following the same procedure, as introduced
earlier with the (2×2) MIMO link, the neighbour an-
tennas correlation coefficients are given by
ρ
(TX)
(k,ℓ)
(φ,ξ) = e
−j2πd
λ
cos(φ)
·e
−
1
2
(2πd
λ
sin(φ)σ
ξ
)
2
. (58)
where (k,ℓ) takes the values (1,2), (2, 3) and (3,4)
corresponding to the four transmit antennas. Fur-
thermore, reciprocity can be assumed, i. e. ρ
(TX)
(k,ℓ)
=
ρ
∗(TX)
(ℓ,k)
.
AnalysisofMIMOSystemswithTransmitter-sideAntennasCorrelation
153
In this paper it is analysed how the antennas corre-
lation impact the MIMO link performance focussing
on the transmitter-side antennas correlation effect.
The correlation coefficients depends on the antennas
spacing, the signal departure angle respect to the ar-
ray axis and the spread angle concerning the scatters
dispersion. It has been shown (see Fig. 3– 5) that the
correlation effect increases as the antennas’ separa-
tion diminishes. Furthermore, the correlation effect
diminishes as the departure angle increases. On the
other hand, the larger the spread angle the lower the
correlation coefficient.
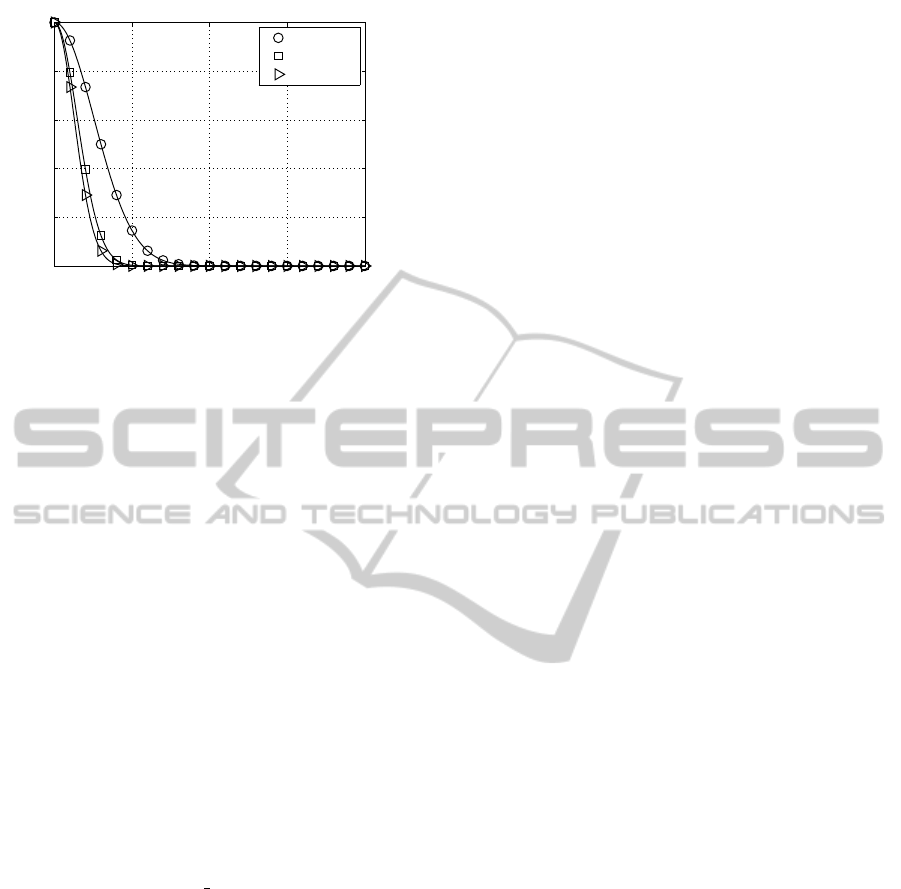
As the singular values decomposition is used to
pre- and post-processing of the system signals in or-
der to avoid inter-antenna interferences, the impact of
antennas correlation on the singular values has been
analysed (see Fig. 8–9). By applying the SVD, the
MIMO channel can be described as multiple indepen-
dent SISO channels (so called layers) with different
gains (given by the corresponding singular values).
For the same noise power at the receive antenna, the
larger the singular value the higher is the SISO chan-
nel reliability. The ideal situation is when all sin-
gular values are equal. The apparition of predomi-
nant layers (high valued singular value) is accompa-
nied by weak layers (low valued singular value). As
highlighted in Fig. 8 and 9, the difference between
the the smallest and the largest layer-specific singular
value becomes smaller as the antennas correlation in-
creases. The antennas correlation effect increases the
probability of having predominant layers.
0 0.2 0.4 0.6 0.8 1
0
0.002
0.004
0.006
0.008
0.01
uncorrelated
correlated
pdf →
singular value →
Figure 8: PDF (probability density function) of the ratio ϑ
between the smallest and the largest singular value for cor-
related (solid line) as well as uncorrelated (dotted line) fre-
quency non-selective (2×2) MIMO channels (d
λ
= 1/32,
φ = 30
◦
rad and σ
ξ
= 1,0).
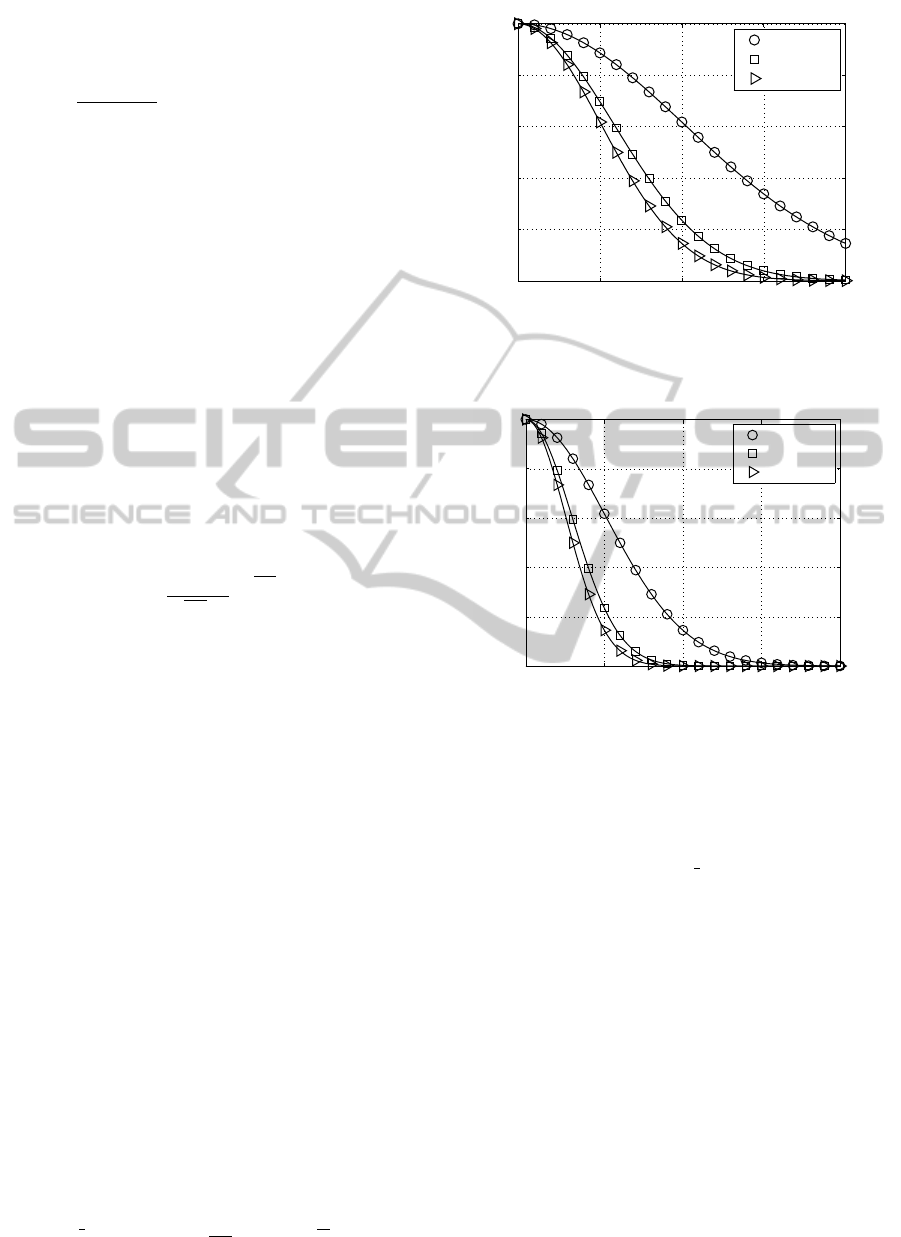
In order to show the distribution of the layer-
specific characteristic properly, the CCDF (comple-
mentary cumulative distribution function) is used (see
0 0.1 0.2 0.3 0.4 0.5
0
0.002
0.004
0.006
0.008
0.01
uncorrelated
correlated
pdf →
singular value →
Figure 9: PDF (probability density function) of the ratio ϑ
between the smallest and the largest singular value for cor-
related (solid line) as well as uncorrelated (dotted line) fre-
quency non-selective (4×4) MIMO channels (d
λ
= 1/32,
φ = 30
◦
rad and σ
ξ
= 1,0).
0 1 2 3 4 5 6
0
0.2
0.4
0.6
0.8
1
p
ξ
1
(1st layer)
p
ξ
2
(2nd layer)
p
ξ
3
(3rd layer)
p
ξ
4
(4th layer)
Prob{
p
ξ
ℓ
≥U} →
U →
Figure 10: CCDF of the layer-specific distribution for cor-
related (solid line) as well as uncorrelated (dotted line) fre-
quency non-selective (4×4) MIMO channels (d
λ
= 1/32,
φ = 30
◦
rad and σ
ξ
= 1,0).
Fig. 10). It can be noticed the different effect on
strong and weak layers. The antennas correlation in-
creases the probability of having layers with larger
values (see layers
p
ξ
1
and
p
ξ
2
) and increases for
weak layers the probability of having lower values
(see layers
p
ξ
3
and
p
ξ
4
).
5 CONCLUSIONS
Due to the proximity of transmitter and receiver side
antenna arrays the theoretically possible potential of
MIMO is significantly reduced by correlation. As
shown by computer simulations, under the effect of
correlation, the influence of layers with high weight-
ing factors becomes even stronger whereas the influ-
ence of layer with low weighting factors diminished.
PECCS2013-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
154

Our results show that not necessarily all layers might
be used for the data transmission even when the wave-
propagation between the different pairs of transmit
and receive antennas is affected by correlation.
REFERENCES
Ertel, R., Cardieri, P., Sowerby, K. W., Rappaport, T. S.,
and Reed, J. H. (1998). Overview of Spatial Channel
Models for Antenna Array Communication Systems.
IEEE Personal Communications, 5(1):10–22.
Haykin, S. S. (2002). Adaptive Filter Theory. Prentice Hall,
New Jersey.
Laub, A. J. (2005). Matrix Analysis for Scientists and Engi-
neers. Society for Industrial and applied Mathematics,
Philadelphia.
Lee, W.-Y. (1973). Effects on Correlation between two Mo-
bile Radio Base-Station Antennas. IEEE Transactions
on Vehicular Technology, 22(4):130–140.
Oestges, C. (2006). Validity of the Kronocker Model for
MIMO Correlated Channels. In Vehicular Technology
Conference, volume 6, pages 2818–2822, Melbourne.
Salz, J. and Winters, J. H. (1994). Effect of Fading Correla-
tion on adaptive Arrays in digital Mobile Radio. IEEE
Transactions on Vehicular Technology, 43(4):1049–
1057.
Shiu, D., Foschini, G., Gans, M., and Kahn, J. (2000). Fad-
ing Correlation and its Effect on the Capacity of Mul-
tielement Antenna Systems. IEEE Transactions on
Communications, 48(3):502–513.
Taparugssanagorn, A., Jasma, T., and Ylitalo, J. (2006).
Spatial Correlation and Eigenvalue Statistics Investi-
gation of Wideband MIMO Channel Measurements.
In IEEE 17th International Symposium on Personal,
Indoor and Mobile Radio Communications (PIMRC),
pages 1–5.
Wang, H., Wang, P., Ping, L., and Lin, X. (2009). How
Does Correlation Affect the Capacity of MIMO Sys-
tems with Rate Constraints? In IEEE Global Telecom-
munications Conference (GLOBECOM), pages 1–5.
Yueyu, W. and Lili, G. (2007). Analysis on Spatial Corre-
lation Related with Antenna Array of MIMO System.
In International Conference on Wireless Communica-
tions, Networking and Mobile Computing (WiCom),
pages 456–459.
AnalysisofMIMOSystemswithTransmitter-sideAntennasCorrelation
155
