
A Genetic Algorithm to Study a P3 Non-trivial Collective Task
F. Jim´enez-Morales
1
and J. L. Guisado
2
1
Dep. F´ısica Materia Condensada, University of Sevilla, Avda. Reina Mercedes s/n, Sevilla, Spain
2
Departamento de Arquitectura y Tecnolog´ıa de Computadores, Universidad de Sevilla, Sevilla, Spain
Keywords:
Cellular Automata, Genetic Algorithm, Non-trivial Collective Behaviour, Period-3.
Abstract:
Here we report new results of a genetic algorithm (GA) used to evolve one dimensional Cellular Automata
(CA) to perform a P3 non-trivial collective behavior task. For this task the goal is to find a CA rule that
reaches one final configuration in which the concentration of active cells oscillates among three different
values. Though the majority of the best evolved rules belong to the II Wolfram’s class, the GA also finds rules
of the III and IV classes. The different computational mechanisms used by each rule to synchronize the entire
lattice are analyzed by means of the spatio-temporal patterns generated.
1 INTRODUCTION
Many natural and man-made systems that consist of
a decentralized collection of simple units with local
interaction can display complex emergent behavior.
The term emergent behavior refers to the appearance
in the system’s temporal behavior of information-
processing capabilities that are not explicitly repre-
sented in the system’s elementary components. These
decentralized systems have many advantages when
compared with central control systems and there is
both a practical and a theoretical interest in the study
of how to design such sytems and their interactions in
order to produce a useful emergent behavior.
One of the most popular methods for the analy-
sis of spontaneous emergence of ordered behavior in
spatially extended systems that are locally coupled
is the use of cellular automata (CA) and genetic al-
gorithms (GA) developed by the “Evolutionary Cel-
lular Automata (EVCA)” group of M. Mitchell, J.P.
Crutchfield and their colleagues (Mitchell et al., 1993;
Mitchell et al., 1994; Crutchfield and Mitchell, 1995;
Das et al., 1994; Das et al., 1995). In their studies a
CA performing computations means that the input to
the computation is seen as the initial state of each cell
and the output is the final state reached by the iter-
ations. They analyzed two computational tasks such
as the density classification and the synchronization
tasks in one dimensional binary CA. For the density
classification task the goal is to find a CA rule that de-
termines whether or not the initial configuration con-
tains more cells in state 1 than cells in state 0. If it
does, the whole lattice should eventually iterate to the
fixed point configuration of all cells in state 1; oth-
erwise it should eventually iterate to the fixed-point
configuration of all 0s. For the synchronization task
a successful CA will reach a final configuration in
which all cells oscillate between all 0s and all 1s on
successive time steps.
In this paper we focus in another computational
task for one dimensional CA such as the period-3 task
in which the goal is to find a rule that, starting from a
random initial condition, reaches one final configura-
tion in which the entire lattice oscillates among three
different states. Originally (Jim´enez-Morales, 1999;
Jim´enez-Morales, 2000) this task was successfully
used to study the appearance of non-trivial collective
behavior in three dimensional CA and in (Jim´enez-
Morales et al., 2002) we made a preliminary study
in one dimension, also the computational mechanics
of an evolved rule was fully described in (Jim´enez-
Morales and Tomassini, 2004). In this paper we use
the same evolutionary process to evolve a population
of one dimensional CA to perform the P3 task but we
report here other answer rules that show irregular and
chaotic patterns.
The paper is organized as follows: section 2 de-
scribes the P3 task, section 3 outlines the character-
istics of our genetic algorithm, the results are shown
in section 4 and finally the conclusions are shown in
section 5.
250
Jiménez-Morales F. and L. Guisado J..
A Genetic Algorithm to Study a P3 Non-trivial Collective Task.
DOI: 10.5220/0004179502500256
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 250-256
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Four of the best evolved rules, the rule table hexadecimal code, the type of non-trivial collective behavior, the
Langton’s parameter, the fitness function versus the highest one and the Wolfram’s class. To recover the 128-bit string giving
the output bits of the rule table, expand each hexadecimal digit to binary. The output bits are then given in lexicographic order.
The arrangement of neighbours in the genetic algorithm is |s
i−3
|s
i−2
|s
i−1
|s
i
|s
i+1
|s
i+2
|s
i+3
|.
Symbol Rule Table Hexadecimal Code NTCB λ F(φ)/F(φ
d
) Wolfram’s
Class
φ
a
90001c50-27307066-0820a852-25650800 P3 0.3203 0.12 II
φ
b
21088418-01091108-41038844-10c18080 P3(QP3) 0.2109 0.41 II
φ
c
f193800-c06b0eb0-e000461c-80659c11 P3 0.3359 0.05 IV
φ
d
146157d1-fbb53fec-7dfbeffc-eaf0fa28 P3 0.6250 1.0 III
2 THE COMPUTATIONAL P3
TASK
2.1 Cellular Automata
Cellular automata are discrete dynamical systems
consisting of an array of cells, each of which can be
in one of a finite number k of possible states, up-
dated synchronously in discrete time steps, accord-
ing to a local, identical interaction rule. Here we will
only consider Boolean automata for which the cellular
state s ∈ {0,1}. In this work the regular cellular grid
is one-dimensional, i.e. d = 1. The state of a cell at
the next time step is determined by the current states
of the cell itself and of a surrounding neighborhood
of cells and is given by:
s
t+1
i
= φ(s
t
i−r
...,s
t
i
,...s
t
i+r
) φ : k
2r+1
−→ k (1)
where s
t
i
denotes the value of site i at time t, φ rep-
resents the local rule of evolution, and r is the CA
radius i.e., the number of neighbors (cells) on ei-
ther side of a given cell. The configuration of the
entire lattice at a given time t can be described by
s
t
= (s
t
0
,s
t
1
,. . . , s
t
N−1
), where N is the lattice size.
Periodic boundary conditions s
t
N+i
= s
t
i
are used. To
study the spatio-temporal patterns generated by the
CA dynamics, a global update rule Φ can be defined
which applies in parallel to all the cells s
t+1
= Φ(s
t
);
and an ensemble operatorΦ
Φ
Φ which operates on sets of
lattice configurations {s
t
} (Wolfram, 1994).
2.2 Non-trivial Collective Behavior
An interesting situation of emergentbehaviorin CA is
found with the appearance of non-trivialcollectivebe-
havior (NTCB). As CA are governed by local interac-
tions and subjected to noise, it was expected that any
global observable, such as the concentration of acti-
vated cells c(t) =
1
N
∑
N
i
s
i
(t) would show a trivial time
dependence in the limit of infinite size (Bennet et al.,
1990). But several exceptions to this have been found.
The most remarkable one is a quasiperiod three be-
havior (QP3) that exhibits the concentration of rule-
33 automaton in d=3 and other CA in higher space
dimensions (Chat´e and P.Manneville, 1992). This be-
havior is neither transient nor due to the finite size
of the lattice and has been obtained for deterministic
and probabilistic rules. Several attempts have been
made to understand its phenomenology and have ad-
dressed the possible mechanisms by which this puz-
zling collective behavior emerges but yet there is not
any answer to the question of how NTCB can be pre-
dicted from the local rule. Then in (Jim´enez-Morales,
1999) we proposed using a genetic algorithm to the
search in d=3 of CA rules with QP3 periodicity and in
(Jim´enez-Morales and Tomassini, 2004) the same al-
gorithm was used in d=1. Quasiperiodicity is the most
interesting non-trivial collective behavior but in d=1
can only be observed under some specific conditions.
Here we will focus mainly in period-3 collective be-
havior. As stated before for this P3 task the goal is
to find a rule for wich the concentration is oscillating
among three different values, i.e., c(t) = c(t + 3).
3 THE GENETIC ALGORITHM
Our GA begins with a population of P = 20 randomly
generated chromosomes, listing the rule-table output
bits in lexicographic order of neighborhood patterns.
We consider binary CA with periodic boundary con-
ditions. Each CA is represented by a bit string delin-
eating its rule table φ, containing the output bits for all
possible neighborhood configurations. The bit string
is of size 2
7
= 128, resulting in a huge space of 2
128
possible rules. The fitness evaluationfor each CA rule
is carried out on a lattice of N cells starting from a
random initial condition of concentration 0.5. After a
transient time of N/2 time steps, we allow each rule
to run for a maximum number of M iterations. The
AGeneticAlgorithmtoStudyaP3Non-trivialCollectiveTask
251

values of concentration are assembled in groups of 4
consecutive values, noted as c
1
to c
4
, and the fitness
function F(φ) is defined by:
F(φ) =
4
M
M/4
∑
i
1
2
abs[(c
2
−c
1
)(c
4
−c
2
)−(c
3
−c
2
)(c
3
−c
1
)]
i
(2)
The rule’s fitness F(φ) is taken from a geometrical
point of view and it is an average area in the iterative
map, i.e. the graph of c(t + 1) versus c(t). In this
iterative map the area of a period-2 behavior is too
small, almost 0, the area of a noisy period-1 and the
area of an intermittent P2 is higher than that of a P2
and finally a P3 and quasiperiod-3 behaviors have the
highest values.
In each generation: (i) F(φ) is calculated for each
rule φ in the population. (ii) The population is ranked
in order of fitness. (iii) A number E = 5 of the highest
fitness (“elite”) rules are copied without modification
to the next generation. (iv) The remaining P− E = 15
rules for the next generation are formed by single-
point crossover between randomly chosen pairs of
elite rules. The off-springs from each crossover are
each mutated with a probability m = 0.05. This de-
fines one generation of the GA; it is repeated G = 10
3
times for one run of the GA.
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0 250 500 750 1000
λ
Generation
φ
d
φ
c
φ
a
φ
b
Figure 1: The λ parameter of the best rule in each genera-
tion versus the generation for the runs in which φ
a
, φ
b
, φ
c
and φ
d
were encountered.
4 RESULTS
We performed more than 200 different runs of the GA
each with a different random-number seed. In d = 1
the GA is able to find many rules with the desired
behavior, about 10% of the runs ended up with a rule
that showed a P3 collective behavior or a quasiperiod-
3. Table 1 shows four of the best evolved rules, the
rule table hexadecimal code, the λ parameter ( defined
as the fraction of nonzero output bits in the rule table),
0.24
0.28
0.32
0.36
0.24 0.28 0.32 0.36
c(t+1)
c(t)
(a)
0.2
0.25
0.3
0.35
0.4
0.45
0.2 0.25 0.3 0.35 0.4 0.45
c(t+1)
c(t)
(b)
0.45
0.47
0.49
0.51
0.45 0.47 0.49 0.51
c(t+1)
c(t)
(c)
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.1 0.2 0.3 0.4 0.5 0.6 0.7
c(t+1)
c(t)
(d)
Figure 2: The iterative map for the rules: (a) φ
a
, (b) φ
b
,
(c) φ
c
and (d) φ
d
. Lattice size is N = 2000 cells. Transient
times are discarded. The collective behavior for the rules
φ
a
, φ
c
and φ
d
is a period-3 behavior. Rule φ
c
shows two
triangular objects that corresponds to a quasiperiod-3 col-
lective behavior.
the non-trivial collective behavior observed, and the
corresponding Wolfram’s class (Wolfram, 1984).
Figure 1 shows the λ parameter of the best evolved
rule in each generation versus the generation. The ini-
tial population of candidate rules have a random λ be-
tween (0,1). For all runs of the GA in the first 250
generations the best selected rule has a λ which has
small differences with the best evolved rule. It has
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
252

0.2
0.25
0.3
0.35
0.4
0 500 1000 1500 2000
c(t)
t
(a)
0.2
0.25
0.3
0.35
0.4
0.45
0 500 1000 1500 2000
c(t)
t
(b)
0.45
0.47
0.49
0.51
0.53
0 500 1000 1500 2000
c(t)
t
(c)
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0 500 1000 1500 2000
c(t)
t
(d)
Figure 3: The time series of the concentration for the rules
(a):φ
a
, (b):φ
b
, (c): φ
c
and (d):φ
d
. Lattice size is N = 2000.
The initial condition is a random configuration with concen-
tration 0.5.
been suggested (Langton, 1990) that there is a rela-
tionship between the ability of a CA to show complex
behavior and the λ parameter. The basic hypothesis
was that λ correlates with computational capability in
that rules capable of complex computation must be or
are most likely to be found near some critical value
( λ
c
≈ 0.26 ) and also that these rules belong to the
Wolfram’s class IV. Our GA has selected rules with λ
that goes from 0.21 to 0.62 and the majority of them
belong to the II class and some others to the III class.
Only in one run the GA encountered a rule of the IV
class, φ
c
, but it has the lowest fitness. The results from
our evolutionary process do not show any kind of crit-
ical value of λ ( an “edge of chaos” ) for the best fit-
ness rules. In this sense the P3 task confirms the same
result as it was obtained by (Mitchell et al., 1993) for
the density classification task.
The behavior of the best evolved rules is shown in
three plots: a) Figure 2 that shows the iterative map,
i.e. the concentration at time t + 1 versus the concen-
tration at time t. In this iterative map transients points
are discarded to better define the collective behavior.
b) Figure 3 that shows the time series of the con-
centration from the starting time t = 0. And finally c)
Figure 4 that shows a space-time diagram of 258x300
points after a transient of 200 time steps.
Rules φ
a
and φ
c
show a P3 behavior that can be
seen as three well defined clouds of points in the it-
erative map and in the time series of the concentra-
tion, after a transient time, as three different constant
values. The time series of the concentration for rule
φ
b
is different and shows three branches that interact
and mix among them. This behavior lasts for very
long times and as the lattice size increases the be-
havior is better defined. Now the iterative map rather
than three clouds of points is a triangular object and
the collective behavior of rule φ
b
corresponds to a
cuasiperiod-three (QP3) behavior (Jim´enez-Morales
and Tomassini, 2004). The rule with the highest value
of the fitness function is φ
d
. Its concentration also os-
cillates among three values but in a noisy fashion and
its attractor in the iterative map consists in a fuzzy 3-
cycle behavior.
Under the fitness function F(φ) in d = 1 the evo-
lutionary process has selected rules that starting from
a random initial condition synchronize the whole sys-
tem to a state in which the concentration oscillates in a
three-state cycle. But the way in which the four rules
obtain the synchronization is quite different from rule
to rule. To understand those mechanisms we can use
the tools of the “computational mechanics” developed
by Crutchfield and Hanson (Hanson and Crutchfield,
1997). This point of view describes the computa-
tion embedded in the CA space-time configuration in
terms of domains, defects and defect interactions.
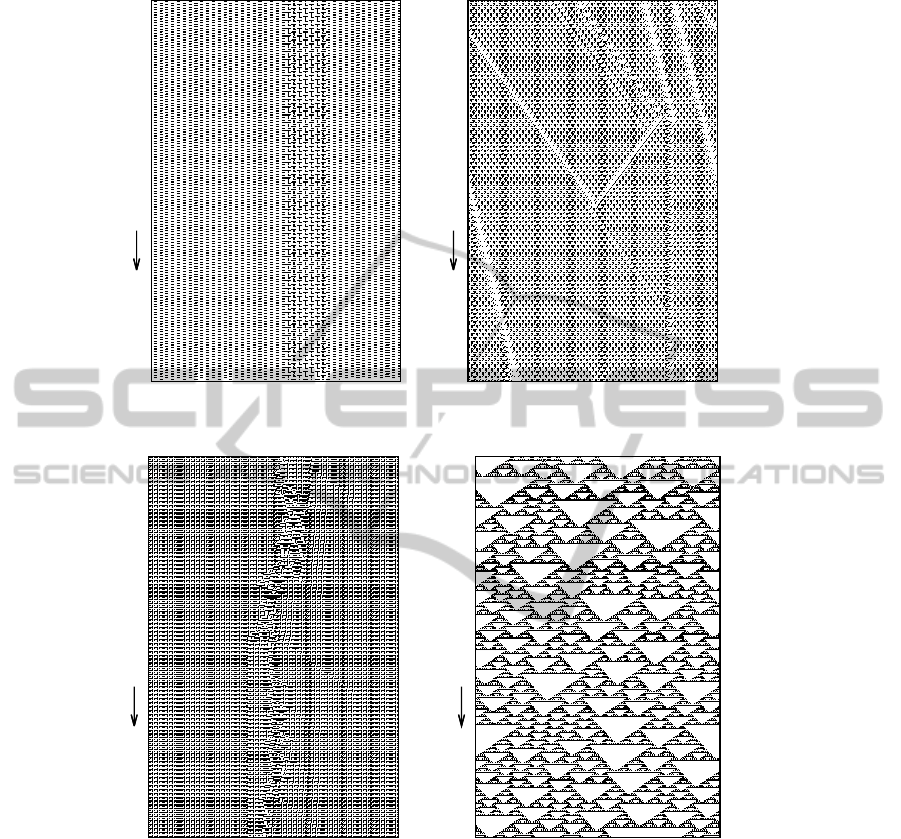
Figure 4a,b shows a space-time diagram of the
rules φ
a
and φ
b
. Time starts after a transient time of
200 time steps and goes from up down and space is
displayed on the horizontal axis. In the patterns gen-
erated by both rules there are some easily recognized
spatio-temporally periodic background -the domains-
on which some dislocations move. A domain, Λ
Λ
Λ, is a
set of configurations with two properties: (i) temporal
AGeneticAlgorithmtoStudyaP3Non-trivialCollectiveTask
253
Time
Space
(a)
Time
Space
(b)
Time
Space
(c)
Time
Space
(d)
Figure 4: Space-Time diagram of four answer CA rules for the computational P3 collective task. Lattice size of 258 cells.
Starting from a random initial condition with c(0) = 0.5 the first 200 time steps are discarded. It is shown a window of
258x300 points. (a) φ
a
. This rule of the II class shows a regular and periodic final state with two fixed domains; (b) φ
b
. This
is also a rule of the II class with a periodic background in which defect cells or particles propagate from distant parts of the
lattice; (c) φ
c
. It can be seen long-lived and irregular propagating defect cells characteristic of the IV class. (d) φ
d
. This is a
chaotic rule ( III class ) that has the highest fitness.
invariance, which means that for some finite temporal
period p, Φ
Φ
Φ
p
Λ
Λ
Λ = Λ
Λ
Λ; and (ii) spatial homogeneity. In
the simplest case a domain consists of a set of cells in
the space-time diagram that are always repeated; for
example, the domain for rule φ
b
is shown in Table 2.
If over a long time all the cells of the space-time dia-
gram are in the domain then the concentration of acti-
vated cells will be oscillating among three values 1/2,
1/3 and 1/6. Displacements of the domains along the
temporal or the spatial axis give place to other do-
mains and at the boundaries between them appear de-
fect cells or particles that propagate among the entire
lattice. These defect cells are spatially localized struc-
tures and time-invariant for rules φ
a
and φ
b
.
But the space time diagram of rules φ
c
and φ
d
(Figure 4c-d) is not so simple as the previous ones.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
254

Rule φ
c
also has a periodic background that fulfils the
requirements of having a period-3 oscillating concen-
tration, but the main difference with φ
a
and φ
b
is the
way the global coordination is acquired. The defect
cells for rule φ
c
are irregular propagating structures,
which is a characteristic of rules that belong to the IV
Wolfram’s class. And finally are the patterns gener-
ated by the rule φ
d
where there is a lack of regularity
or periodic background. While rules φ
a
, φ
b
and φ
c
evolve towards a final state in which the concentra-
tion reaches a well determined three state, the three
values of the concentration for rule φ
d
show a noisy
behavior ( Figure 3d). Rule φ
d
is a chaotic rule and its
behavior may be interesting from an statistical point
of view, though this is out of the scope of this work.
Table 2: Domain for rule φ
b
and the concentration.
Space
1 1 0 1 0 0 c
1
= 1/2
T 1 1 0 0 0 0 c
2
= 1/3
i 0 1 0 0 0 0 c
3
= 1/6
m 1 0 0 1 1 0 c
1
= 1/2
e 0 0 0 1 1 0 c
2
= 1/3
0 0 0 0 1 0 c
3
= 1/6
5 CONCLUSIONS
The study of non trivial collective behavior in CA
has suggested a new computational task like the P3
task. A genetic algorithm, with the appropriate fitness
function, has been able to find answer rules that have
regular repeating space-time configurations. These
rules, belonging to the Wolfram’s class II, attained the
global coordination among the entire lattice cells with
propagating structures –particles– that interact among
them until a regular and final state is reached. In
the patterns generated by these rules it can be distin-
guished domains and particles like in the density and
the synchronization tasks. And the global coordina-
tion can be explained using the tools of the “computa-
tional mechanics” originally developed by the EVCA
group of Crutchfield and Mitchell.
But our GA has also found some rules ( class III
and IV ) for which the space-time diagrams do not
show a regular pattern. The emergence of a global
computation by these chaotic and complex rules is
very interesting and points out the existence of other
synchronization strategies not well understood yet.
We think that many of the results obtained in tasks
like this one can provide a useful information to es-
tablish a more general framework to study the emer-
gence of global coordination in one dimensional CA.
REFERENCES
Bennet, C. H., Grinstein, G., He, Y., Jayaprakash, C., and
Mukamel, D. (1990). Stability of temporally periodic
states of classical many-body systems. Phys. Rev. A,
41:1932–1935.
Chat´e, H. and P.Manneville (1992). Collective behaviors
in spatially extended systems with local interactions
and synchronous updating. Progress Theor. Phys.,
87(1):1–60.
Crutchfield, J. P. and Mitchell, M. (1995). The evolution of
emergent computation. Proceedings of the National
Academy of Science U.S.A., 92:10742–10746.
Das, R., Crutchfield, J. P., Mitchell, M., and Hanson, J. E.
(1995). Evolving globally synchronized cellular au-
tomata. In Eshelman, L. J., editor, Proceedings of
the Sixth International Conference on Genetic Algo-
rithms, pages 336–343, San Francisco, CA. Morgan
Kaufmann.
Das, R., Mitchell, M., and Crutchfield, J. P. (1994). A ge-
netic algorithm discovers particle-based computation
in cellular automata. In Davidor, Y., Schwefel, H.-
P., and M¨anner, R., editors, Parallel Problem Solving
from Nature—PPSN III, volume 866, pages 344–353,
Berlin. Springer-Verlag (Lecture Notes in Computer
Science).
Hanson, J. E. and Crutchfield, J. P. (1997). Computational
mechanics of cellular automata: An example. Physica
D, 103:169–189.
Jim´enez-Morales, F. (1999). Evolving three-dimensional
cellular automata to perform a quasiperiod-3(p3) col-
lective behavior task. Phys. Rev. E, 60(4):4934–4940.
Jim´enez-Morales, F. (2000). The evolution of 3-d c.a.
to perform a collective behavior task. In Miller,
J., Thompson, A., P.Thompson, and Fogarty, T. C.,
editors, Evolvable Systems: From Biology to Hard-
ware ICES-2000, LNCS 1801, pages 90–102, Berlin.
Springer-Verlag.
Jim´enez-Morales, F., Mitchell, M., and Crutchfield, J.
(2002). Evolving one dimensional cellular automata
to perform non-trivial collective behavior task: One
case study. In Sloot, P., Tan, C. K., Dongarra, J., and
Hoekstra, A., editors, Computational Science ICSS-
2002, LNCS 2331, pages 793–802, Berlin. Springer-
Verlag.
Jim´enez-Morales, F. and Tomassini, M. (2004). Glob-
ally synchronized oscillations in an one-dimensional
cellular automaton. Int. Jour. Modern Physics C,
15(3):409–425.
Langton, C. G. (1990). Computation at the edge of chaos:
Phase transitions and emergent computation. Physica
D, 42:12–37.
Mitchell, M., Crutchfield, J. P., and Hraber, P. T. (1994).
Evolving cellular automata to perform computations:
Mechanisms and impediments. Physica D, 75:361 –
391.
Mitchell, M., Hraber, P. T., and Crutchfield, J. P. (1993). Re-
visiting the edge of chaos: Evolving cellular automata
to perform computations. Complex Systems, 7:89 –
130.
AGeneticAlgorithmtoStudyaP3Non-trivialCollectiveTask
255

Wolfram, S. (1984). Universality and complexity in cellular
automata. Physica D, 10:1.
Wolfram, S. (1994). Cellular Automata and Complexity.
Addison-Wesley, USA, first edition.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
256
