
Memetic Algorithm with Population Management
for the Two-dimensional Loading Vehicle Routing Problem
with Partial Conflicts
Khaoula Dhaoui, Nacima Labadie and Alice Yalaoui
LOSI-ICD-UMR-STMR-CNRS, University of Technology of Troyes, Troyes, France
Keywords:
Vehicle Routing, Bin-packing, Partial Conflicts, Memetic Algorithm.
Abstract:
The two-dimensional loading vehicle routing problem with partial conflicts combines two NP-hard problems:
the capacitated vehicle routing problem (CVRP) and the two-dimensional bin-packing problem with partial
conflicts (2BPPC). This problem arises for example in hazardous waste collection, where some materials
can be partially conflicting. In this paper, we propose a memetic algorithm with population management to
resolve this new problem. A modified SHF-D heuristic is used to obtain feasible packing in each vehicle. The
proposed approach is tested on a new benchmark, created by adding partial conflicts to instances from the
literature.
1 INTRODUCTION
Some recent works have been dedicated for coupling
vehicle routing and items packing in the vehicles to
obtain solutions for the two-dimensional loading ca-
pacitated vehicle routing problem (2L-CVRP). This
problem was proposed for the first time by Iori et
al. (Iori, 2004) who developed an exact method (Iori
et al., 2007) to solve it. Several approximate methods
were proposed by Gendreau et al. (Gendreau et al.,
2008), Zachariadis et al. (Zachariadis et al., 2009),
Leung et al. (Leung et al., 2011), Fueller et al. (Fu-
ellerer et al., 2009) and Duhamel et al. (Duhamel
et al., 2011). In all previous studies, the authors
solved a basic two-dimensional bin-packing problem
for each vehicle.
Khebbache et al. (Khebbache et al., 2011) studied
the 2L-CVRP with time windows. The authors pro-
posed six heuristics and metaheuristics for this vari-
ant. The three dimensional case refereed to as 3L-
CVRP with time windows was also investigated by
Moura et al. (Moura and Oliveira, 2009) and (Moura,
2008).
The concept of distance constraint was introduced
by several authors in studies dedicated to packing
problems. In (Stoyan and Yaskov, 1998), each item
has to be separated from all the other items and from
the bin borders by a given distance, depending on
the item. Therefore, there is no contact between the
edges of all items. These authors (Stoyan and Yaskov,
1998) proposed a mathematical model and a com-
bination of a branch and bound and a reduced gra-
dient method to solve this problem. They consid-
ered both the cases where the items are either rect-
angles or circles. The problem was generalized to
the three dimensional case by Stoyan and Chugay
(Stoyan and Chugay, 2009). In this last study, items
are either cylinders or parallelepipeds and the packing
area is considered of some given shape. In (Beaumont
et al., 2010), the maximal distance between two items
packed in the same bin has to be smaller than a given
threshold.
In some industrial applications such as in Haz-
ardous Material (HazMat) transportation, residues of
HazMat are first decanted into rectangular or circu-
lar containers at their source, then the schedule of the
containers transshipment to reprocessing plants is or-
ganized. According to HazMat classification, some
products can be partially conflicting. In this case
these materials can be stored or shipped together, but
they have to be separated by a given safety distance.
Some HazMat can also be in total conflict, it is then
not permitted to store them in the same warehouse or
transport them in the same vehicle. In HazMAt trans-
portation legislation, one horizontal meter distance
have to be kept between any two partially conflicting
materials. This industrial application motivated us to
introduce the two-dimensional bin-packing problem
with partial conflicts (2BPPC), for which a mathemat-
ical model, several heuristics and a multi-start genetic
189
Dhaoui K., Labadie N. and Yalaoui A..
Memetic Algorithm with Population Management for the Two-dimensional Loading Vehicle Routing Problem with Partial Conflicts.
DOI: 10.5220/0004149501890195
In Proceedings of the 4th International Joint Conference on Computational Intelligence (ECTA-2012), pages 189-195
ISBN: 978-989-8565-33-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

algorithm were proposed (Dhaoui et al., 2012).
This paper provides a first study for the two di-
mensional loading with partial conflicts capacitated
vehicle routing problem (2LPC-CVRP). The resolu-
tion approach proposed here combines a memetic al-
gorithm for the routing problem and a heuristic for
the packing. In Section 2, the two problems (vehi-
cle routing and 2-dimensional bin-packing with par-
tial conflicts) are presented. In Section 3, the different
components of the memetic algorithm are explained.
Section 4 is dedicated to computational results and a
conclusion ends this paper.
2 PROBLEM PRESENTATION
2.1 Vehicle Routing Problem
The capacitated vehicle routing problem can be de-
fined on an undirected graph G = (V, E) with V = {0,
1,..., n} the set of vertices and E the set of edges. The
vertex 0 represents the depot, where a fleet of K iden-
tical vehicles with capacity Q is provided, whereas the
other vertices represent the customers. A demand d
i
is associated to each customer i and a traveling cost
c
i j
is associated to each edge [i,j].
Given the graph G, the vehicle routing problem
consists in finding the routes satisfying the following
constraints: each route starts and ends at the depot,
each customer is visited only once by a single vehi-
cle and the total demand of customers assigned to the
same route can not exceed the vehicle capacity Q. The
aim is to minimize the total traveling cost. The objec-
tive function is defined as follows:
K
∑
k=1
n
∑
i=1
n
∑
j=1
c
i j
.x
k
i j
(1)
Where x
k
i j
is a binary variable that takes the value 1
when the edge [i,j] is crossed by the vehicle k going
from i to j.
2.2 Two-dimensional Packing Problem
with Partial Conflicts
This problem has been studied for the first time by
Dhaoui et al. (Dhaoui et al., 2012). A 2BPPC instance
consists in a set A = {1, ..., n} of items which have to
be packed in a minimum number of identical bins. A
bin is defined by its height H and its width W . An
item i has a height h
i
and a width w
i
(h
i
, w
i
∈ IN) and
may be in partial conflict with some other specified
items. A solution of the problem consists in assign-
ing each item i to a bin and defining its position, de-
noted by (x
i
, y
i
) which corresponds to the coordinates
of its bottom left-hand corner in the bin, without over-
lapping while keeping a safety distance D between
partially conflicting items (Figure 1). The considered
distance is denoted d
∞
and is defined as follows: let
i and j be two items inserted in the same bin and as-
sume that their positions in the bin are: (x
i
, y
i
) and
(x
j
, y
j
). d
∞
(i, j) = max{|x
i
− x
j
|, |y
i
− y
j
|}.
In this study, the distance d
∞
is chosen because it
is the one often used in hazardous material transporta-
tion. In this sector, the guideline is to keep a prefixed
horizontal or vertical spacing between any two ma-
terials partially conflicting. For example, corrosive
material and flammable solid material are in partial
conflict as indicated in Hazardous material classifica-
tion data-base (Environment Canada, 2002). hence,
when they have to be packed within the same bin (a
storage area or a vehicle), a safety distance of 1 hori-
zontal or vertical meter must separate them. Figure 1
shows the difference on using the distance d
∞
and the
Euclidean distance d.
This study is dedicated to a new problem, the
2LPC-CVRP which is a combination of both vehi-
cle routing optimization and two-dimensional pack-
ing of items with partial conflicts. In this work, non-
sequential (unrestricted) packing without items rota-
tion is considered.
Figure 1: Safety distance.
In Figure 2, items 1 and 2 are conflicting with item
i, that is why a safety distance D is kept between them.
Figure 2: Partial conflicts.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
190

3 MEMETIC ALGORITHM WITH
POPULATION MANAGEMENT
In this section, the different components of our
memetic algorithm (MA) are detailed. First, an ini-
tial population of NP chromosomes is generated. A
chromosome is coded as a sequence of n customers (a
permutation) without route delimiters, which can be
seen as a giant tour violating the capacity and pack-
ing constraints. A feasible solution of our problem is
obtained by cutting this giant tour into feasible routes
using a Cutting Procedure. The parent solutions are
selected with a binary tournament and crossed over to
obtain child solutions or offsprings. A local search is
applied with a given probability to improve the solu-
tions quality. Finally, the acceptance or rejection of
new solutions is decided by the population manage-
ment procedure. The best NP solutions constitute the
new population. This treatment is repeated NG times.
3.1 Initial Solutions
A first solution is computed with an adaptation of
Clarke and Wright heuristic (Clarke and Wright,
1964) and is then converted to a chromosome by con-
catenating its routes. The resulting chromosome is in-
cluded in the initial population which is completed by
generating randomly the (NP -1) remaining elements.
Each chromosome in the population is evaluated us-
ing the cutting procedure explained in section 3.3.
3.2 Crossover
Parents are selected by binary tournament method:
two chromosomes are randomly selected in the popu-
lation and the best one is the first parent. This process
is repeated to get the second parent. Then they are
combined using the classical operator OX for Order
Crossover (Goldberg, 1989). OX begins by randomly
selecting two break points i and j (1 < i ≤ j < n) in
the first parent. Customers located between the posi-
tions i and j in the first parent are copied into the child
chromosome in the same positions. The remaining
customers are added by browsing the second parent
from left to right and are copied in the order of their
appearance. Each crossover provides a single child.
The fitness of the obtained child solution is then com-
puted using the Cutting Procedure.
3.3 Cutting Procedure
This procedure starts by applying the method called
Split proposed by Prins (Prins, 2004) for the CVRP.
Split consists in computing a shortest path in an aux-
iliary graph containing a dummy vertex 0 and a ver-
tex for each customer. The packing feasibility of the
obtained routes is checked with a modified version
of SHF-D heuristic. Infeasible routes (for the pack-
ing problem) are concatenated to obtain a new gi-
ant route (or a sub-chromosome). For this new se-
quence, a new packing heuristic is performed: cus-
tomers are assigned to routes in the order given by the
sub-chromosome. When the customer’s demand can’t
be packed in all the available vehicles, a new route is
created and this later is initialized with this customer.
A feasible solution for the 2LPC-CVRP is obtained at
the end of this procedure.
3.4 Population Management
To avoid premature convergence of the population to
a local minimum, it is possible to use a management
tool that allows to choose whether to keep or reject
a solution according to a distance criterion from the
existing solutions. Memetic algorithms with popula-
tion management have been introduced by S
¨
orensen
and Sevaux (S
¨
orensen and Sevaux, 2006). We con-
sider the distance computing the number of ”broken
pairs” as introduced in (Mart
`
ı et al., 2005). Let con-
sider two chromosomes X and Y . The customer that
occupies the position i in the chromosome X is de-
noted X
i
. The distance D(X,Y ) equals the number of
pairs {X
i
, X
i+1
} that are not adjacent in Y . The dis-
tance of a chromosome to a population P is defined as
follows:
D
P
(Y ) = min{D(X,Y ) : X ∈ P} (2)
A new solution Y is accepted in the population P
if its distance from the population is greater than a
given level ∆. When ∆ equals 0, it simply consists in
eliminating copies. The management procedure starts
by sorting the chromosomes of a population P in a
decreasing order of their quality, which corresponds
to increasing order of costs. The population size is
constant, that means when a new solution is accepted,
another solution is eliminated. To maintain the best
found solutions, the solution to be eliminated is se-
lected randomly in the worst half of the population.
The level ∆ is then updated based on the rate of re-
fusal or acceptance of solutions (when more than M
solutions are accepted, ∆ is increased by one unit,
and when more than M solutions are rejected, ∆ is
decreased by one unit).
MemeticAlgorithmwithPopulationManagementfortheTwo-dimensionalLoadingVehicleRoutingProblemwithPartial
Conflicts
191

3.5 Modified Shelf Heuristic
Fill-Dynamic (SHF-D)
This heuristic was introduced by Ben Messaoud et al.
(BenMessaoud et al., 2004) and is mainly used for
guillotine cutting problems. In this kind of problems,
the cutting tool has to go from one edge of the rectan-
gle (or the strip to cut) to the other. Shelf algorithms
allow to resolve this problem. Packing is obtained by
inserting items from the left to the right side, while
forming shelfs. The first shelf corresponds to the rect-
angle bottom. The next shelf bottom is obtained with
the horizontal line that coincide with the top of the
highest item in the previous shelf. The treatment is re-
peated for all items. The modified version presented
in this section was proposed for the 2BPPC by Dhaoui
et al. (Dhaoui et al., 2012).
In the classical version, items are sorted out in
a decreasing order of heights. In this modified ver-
sion, items are separated into sets corresponding to
their classes (as in hazardous materials classification,
items are assigned to classes and the partial conflicts
are rather defined between classes than items). Then
they are inserted in a way that the items of two classes
treated successively are not conflicting. If it is im-
possible to obtain an order that separates every pair
of conflicting classes, a safety distance is kept when
necessary.
The procedure that sorts out the classes starts by
assigning the first position to the class that has the
biggest degree of conflicts. The degree of conflicts of
a class corresponds to the number of classes conflict-
ing with it. After adding a class to the list, the follow-
ing class is chosen among the classes non conflicting
with it.
The procedure sorting out the classes is described
in Algorithm 1. Classes stands for the table of classes
and represents the input of the algorithm, while List
is the output corresponding to the new order of the
classes. Nc is the number of classes and c and ind
are indexes of the classes. Degree is a table in which
are recorded the degree of the classes. Finally, Com-
patible is a boolean that takes the value true if the
considered classes are compatible, and the value false
if not.
Each item is inserted in the lowest possible po-
sition left-justified in the first shelf where it fits en-
tirely, if any. If none of the existing shelfs can contain
it, a new shelf is initialized. This heuristic is differ-
ent from other classical shelf algorithms with its ten-
dency to reuse at best the free areas in each shelf, by
inserting items on top of the others while preserving
guillotine cutting constraints.
At any stage of the heuristic, each used bin con-
Algorithm 1: Sorting out classes Procedure.
Sort out Classes in a decreasing order of Degree
c = 1
List(c) = Classes(c)
Repeat
ind = c + 1
Compatible = false
Repeat
If (Classes(ind) conflicts with List(c)) then
ind = ind + 1
Else Compatible = true
Until ((Compatible = true) or (ind = Nc))
If (Compatible = true) then List(c) =
Classes(ind)
Else List(c) = Classes(c+1)
c = c + 1
Until (c = Nc)
tains a set of empty spaces. These spaces are available
rectangles; each of them is defined with its height,
width and coordinates of its bottom left corner. To
place an item, the method proceeds by examining
each available rectangle in turn and finding whether
the item fits into it and whether it is conflicting with
the already packed items that surround the considered
rectangle. Rectangles are examined in an increasing
order of the ordinates of their bottom left corner. In
case of equality, abscissa is considered and the rect-
angle with lowest value of abscissa is examined first.
In Figure 3, after the insertion of item 1, the used
available rectangle is deleted while two new available
rectangles are created: Top (W
1
= W, H
1
= H − y
1
) is
the available rectangle on top of the inserted item and
Right (W
2
= W − x
2
, H
2
= H) is the available rectan-
gle on its right.
Figure 3: Available rectangles.
The procedure Update is described in Algorithm
2. Nr is the number of available rectangles. Let p be
the index of the available rectangle where the current
item is inserted. If there is an intersection between
an existing rectangle r and the rectangle p, the di-
mensions of the rectangle r are modified in order to
eliminate the intersection area. If the new height or
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
192

width of the treated rectangle becomes null, the rect-
angle is deleted. Two new rectangles are created (Top
and right) and the rectangle p is deleted.
Algorithm 2: Procedure to update available rectangles.
Create Rectangles (Top) and (Right)
For r = 1 to Nr
If Rectangle(r) ∩ Rectangle(p) 6=
/
0
Update Rectangle(r)
If (W
r
= 0 or H
r
= 0) Delete Rectangle(r)
end for
Delete Rectangle(p)
Sort out Rectangle
In the dynamic version of the method (SHF-D), a
shelf height is not fixed with the height of the first in-
serted item. A temporary height is updated after each
insertion. Let Nr be the number of available rectan-
gles in the current bin and Ns the number of shelfs
within it. If the current item does not fit in all the
Nr − 1 available rectangles and the last rectangle has
to be used (the rectangle with the biggest ordinate of
bottom-left corner), a new shelf is initialized with this
item and the height of the previous shelf is fixed. In
Algorithm 3, let p be the index of the valid rectangle
and Y
p
its ordinate.
Algorithm 3: Fix shelf height Procedure.
If (p = Nr) then
Shelf Height(Ns) = Y
p
Ns = Ns + 1
Initialize Shelf(Ns) with Current Item
else
Insert Current Item in Shelf(Ns)
End if
3.6 Local Search
Three kinds of moves are used, each of them defining
a neighborhood structure. For the moves that concern
two different routes, the packing feasibility is checked
with modified SHF-D and only feasible moves are
performed. The moves are sorted in increasing order
of complexity and are:
Move 1: Customer Relocation
This move type relocates a customer from his current
position to another position. The move can be used
for every possible insertion position, and can involve
only one route or two different routes.
Move 2: Position Exchange
This move type exchanges the routes that cover a
pair of customers. The two customers swap their po-
sitions in the routes too. It is employed for every
pair of routes and for every customer pair involved in
the considered routes. When the move is performed
within a single route, the customers swap their posi-
tions within this route.
Move 3: 2-opt
The move 2-opt is defined by two customers a and
b. Let X be a route represented as a list of customers
containing a copy of the depot in the beginning and
at the end, X = (x
1
= 0, x
2
, ..., x
t
, x
t+1
= 0). Only the
case where a and b are within the same route X with
x
i
= a, x
j
= b and i ≤ j is considered. The move 2-opt
consists in inverting the subsequence (x
i
, x
i+1
, ..., x
j
).
It is replaced by the subsequence (x
j
, x
j−1
, ..., x
i
).
4 EXPERIMENTAL RESULTS
The used computer is a PC Pentium(R) Dual-Core
CPU T4400 2.20 GHz with an operating system Win-
dows 7. For our tests, we adapted the instances of
Iori (Iori, 2004) created for the 2L-CVRP. In these
instances, the number of items and their sizes are cre-
ated in five sets. The first set corresponds to instances
of a capacitated vehicle routing problem (CVRP). In
the set i, with i = 1, ..., 5, the number of items assigned
to each customer ranges from 1 to i. Dimensions of
items are generated according to uniform distribution
in given intervals (Iori et al., 2007). In these instances
the number of customers ranges from 15 to 35, while
the number of items is between 15 and 114.
In order to obtain 2LPC-CVRP instances, each
item is assigned to one of 5 categories of hazardous
materials and a class index is then associated ran-
domly to each item. Partial conflicts are generated
randomly between some classes. The obtained in-
stances are constituted of 16 groups of instances, each
one contains five files.
For the main parameters setting, a design of exper-
iments ”Latin Square” with 9 situations and 3 levels
was used. The parameters are fixed as follows: (NG,
NP, α) = (20, 20, 1), where NG is the number of gen-
erations, NP is the population size and α is the rate of
local search.
The results on the instances considering the con-
flicts into account are given in the table 1. The aim is
to minimize the overall traveling cost (as in the clas-
sical CVRP) when assuming an unlimited number of
vehicles. The obtained total cost and the computing
time are reported.
The algorithm was also tested on the instances
without conflicts in order to estimate its performance
when compared to the best results of the literature ob-
MemeticAlgorithmwithPopulationManagementfortheTwo-dimensionalLoadingVehicleRoutingProblemwithPartial
Conflicts
193
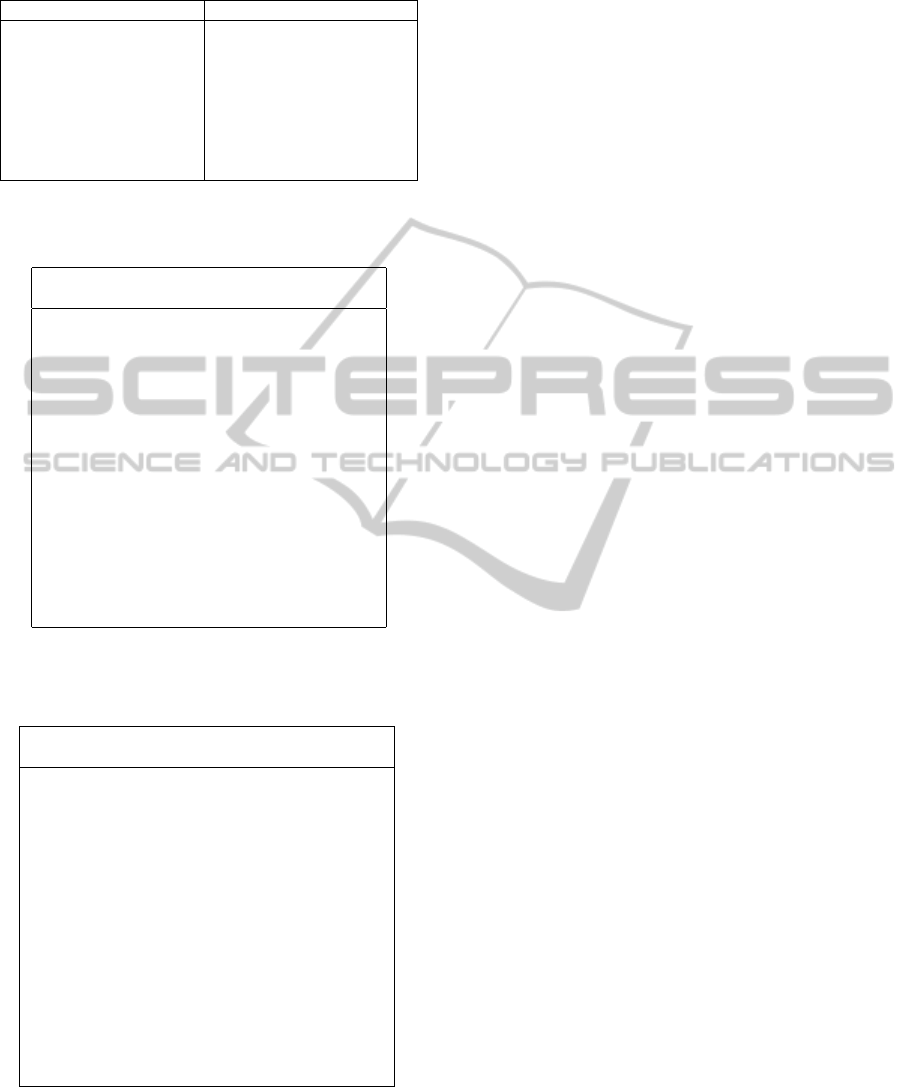
Table 1: Average results of our MA per group of instances.
Group Cost Time Group Cost Time
1 327,85 1,61 9 677,97 4,32
2 370,89 2,80 10 725,66 5,12
3 427,45 1,84 11 683,89 3,84
4 403,49 4,12 12 2232,56 5,66
5 483,41 3,94 13 1593,85 5,78
6 643,60 3,50 14 1308,52 7,14
7 687,91 3,92 15 851,64 4,96
8 848,06 4,10 16 708,10 3,50
Table 2: Average results for set 1 (CVRP) of Iori instances
(groups from 1 to 16).
Groups Best MA
Cost Time Cost Time
1 278,73 0,11 278,73 3,1
2 334,96 0,02 334,96 0,04
3 358,85 0,69 358,85 2,8
4 430,88 0,83 430,88 2,1
5 375,28 0,13 375,28 3,4
6 485,85 0,66 495,85 1.3
7 568,56 0,25 568,56 4
8 568,56 0,19 568,56 3,5
9 607,65 3,97 607,65 4,7
10 535,8 0,59 558,27 4,1
11 505,01 0,8 531,30 4,2
12 610.00 12,6 646,46 3,6
13 2006,3 0,83 2248,21 4,4
14 837,67 0,74 913,18 4,1
15 837,67 1,36 1136,70 2,3
16 698,61 22,8 708,42 4,3
Table 3: Average results for sets from 2 to 5 (2L-CVRP) of
Iori instances (groups from 1 to 16).
Groups Best MA
Cost Time Cost Time
1 284,42 0,90 286,89 1,3
2 339,26 0,10 339,26 1,40
3 376,32 0,50 381,34 2,5
4 435,01 0,20 443,25 1,1
5 379,04 0,10 401,01 5,00
6 497,04 0,40 506,13 4,00
7 691,11 1,40 720,79 3,8
8 678,84 0,80 747,32 3,9
9 612,01 0,60 625,50 1,9
10 675,79 15,10 744,65 5,6
11 705,95 11,30 771,83 5,6
12 611,26 16,90 663,18 4,3
13 2490,62 78,00 2859,10 5,9
14 984,42 79,90 1199,27 7,1
15 1144,69 257,70 1275,25 7,7
16 699,79 6,00 709,75 5,1
tained by Duhamel et al. (Duhamel et al., 2011). For
this purpose, a restriction on the number of vehicles
is added. We consider non-sequential packing with-
out items rotation. In average, our MA has a distance
of 6% from the best known solutions.
In Table 2, the results on the first group of in-
stances are reported. this group corresponds to a pure
transportation problem. Our algorithm finds the best
known solutions for 8 out of 16 instances. The com-
putation time of our MA does not exceed 5 seconds,
while it may be much higher for some results obtained
by Duhamel et al. (Duhamel et al., 2011).
Table 3 gives the average results for sets from 2 to
5. Our algorithm finds the best known average only
for set 2. For the other sets, our results are very close
to the best known results in the literature, particularly
for instances of the first groups (groups 1 to 6). For
8 groups out of 16, the gap is less than 4%. For 7
other groups the gap ranges from 6% to 14%. Only
the gap of the group 14 is over 20%. The average gap
obtained for all studied instances to the best known
solutions is about 6.6%.
5 CONCLUSIONS
This paper presents a first study for the two-
dimensional loading with partial conflicts capacitated
vehicle routing problem. A memetic algorithm with
population management is designed to solve routing
part, while a heuristics is used to solve packing prob-
lem. The first results are promising. Further results
would be given in the conference.
REFERENCES
Beaumont, O., Bonichon, N., and Larchev
ˆ
eque, H. (2010).
Bin packing under distance constraint. Technical re-
port, Universit
´
e de Bordeaux, Laboratoire Bordelais
de Recherche en Informatique, INRIA Bordeaux Sud-
Ouest.
BenMessaoud, S., Chu, C., and Espinouse, M. (2004). An
approach to solve cutting stock sheets. Scottish Math-
ematical Council, 6:5109–5113.
Clarke, G. and Wright, J. (1964). Scheduling of vehicles
from a central depot to a number of delivery points.
Operations Research, 12:568–581.
Dhaoui, K., Labadie, N., and Yalaoui, A. (2012). Algo-
rithms for the two dimensional bin packing problem
with partial conflicts. RAIRO - Operations Reseach,
accepted.
Duhamel, C., Lacomme, P., Quilliot, A., and Toussaint,
H. (2011). A multi-start evolutionary local search
for the two dimensional loading capacitated vehicle
routing problem. Computers & Operations Research,
38(3):617–640.
Environment Canada (2002). Compliance promotion bul-
letin (compro no. 12) - regulations for the manage-
ment of hazardous waste.
IJCCI2012-InternationalJointConferenceonComputationalIntelligence
194

Fuellerer, G., Doerner, K., Hartl, R., and Iori, M. (2009).
Ant colony optimization for the two-dimensional
loading vehicle routing. Computer & Operations Re-
search, 36(3):655–673.
Gendreau, M., Iori, M., Laporte, G., and Martello, S.
(2008). A tabu search heuristic for the vehicle routing
problem with two-dimensional loading constraints.
Networks - Special Issue In Memory of Stefano Pal-
lottino, 51:4–18.
Goldberg, D. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley,
Reading, Massachussett, USA.
Iori, M. (2004). Metaheuristic algorithms for combinato-
rial optimization problems. PhD thesis, University of
Bologna, Italy.
Iori, M., Salazar-Gonzalez, J. J., and Vigo, D. (2007). An
exact approach for vehicle routing problem with two-
dimensional loading constraints. Transportation Sci-
ence, 41(2):253–264.
Khebbache, S., Prins, C., Yalaoui, A., and Reghioui, M.
(2011). Heuristics and memetic algorithm for the two-
dimensional loading capacitated vehicle routing prob-
lem with time windows. Central European Journal
of Operations Research, pages DOI: 10.1007/s10100–
011–0204–9.
Leung, S., Zhou, X., Zhang, D., and Zheng, J. (2011). Ex-
tended guided tabu search and a new packing algo-
rithm for the two-dimensional loading vehicle rout-
ing problem. Computers & Operations Research,
38(1):205–215.
Mart
`
ı, R., Laguna, M., and Campos, V. (2005). Scatter
search vs genetic algorithms: an experimental eval-
uation with permutation problems. Metaheuristic Op-
timization via Memory and Evolution: Tabu Search
and Scatter Search, Boston, Kluwer. C. Rego and B.
Alidaee, editors.
Moura, A. (2008). A multi-objective genetic algorithm for
the vehicle routing with time windows and loading
problem. Intelligent Decision Support, pages 187–
201.
Moura, A. and Oliveira, J. F. (2009). An integrated ap-
proach to the vehicle routing and container loading
problems. Operations Research Spectrum, 31(4):775–
800.
Prins, C. (2004). A simple and effective evolutionary algo-
rithm for the vehicle routing problem. Computers and
Operations Research, 31:1985–2002.
S
¨
orensen, K. and Sevaux, M. (2006). MA|PM: Memetic
algorithms with population management. Computers
and Operations Research, 33(5):1214–1225.
Stoyan, Y. and Chugay, A. (2009). Packing cylinders and
rectangular parallelepipeds with distances between
them into a given region. European Journal of Op-
erational Research, 360(197):446–455.
Stoyan, Y. G. and Yaskov, G. N. (1998). Mathematical
model and solution method of optimization problem
of placement of rectangles and circles taking account
special constraints. International Transactions on Op-
erational Research, 5(1):45–57.
Zachariadis, E., Tarantilis, C., and Kiranoudis, C. (2009).
A guided tabu search for the vehicle routing problem
with two-dimensional loading constraints. European
Journal of Operational Research, 195(3):729–743.
MemeticAlgorithmwithPopulationManagementfortheTwo-dimensionalLoadingVehicleRoutingProblemwithPartial
Conflicts
195
